漂亮实用的15个脑图模板,你知道哪些是AI做的吗?
对于很多第一次接触到思维导图的朋友,看到软件的时候往往找不到方向,不知道如何创作?
今天大家的好助手来了。
一是有大量的思维导图模板,大家看着模板做,慢慢就会做了。
二是ProcessOn 思维导图已经可以用AI 做思维导图了,只要输入关键词,就可以一键生成思维导图非常方便。
1、《22条商规》精简版
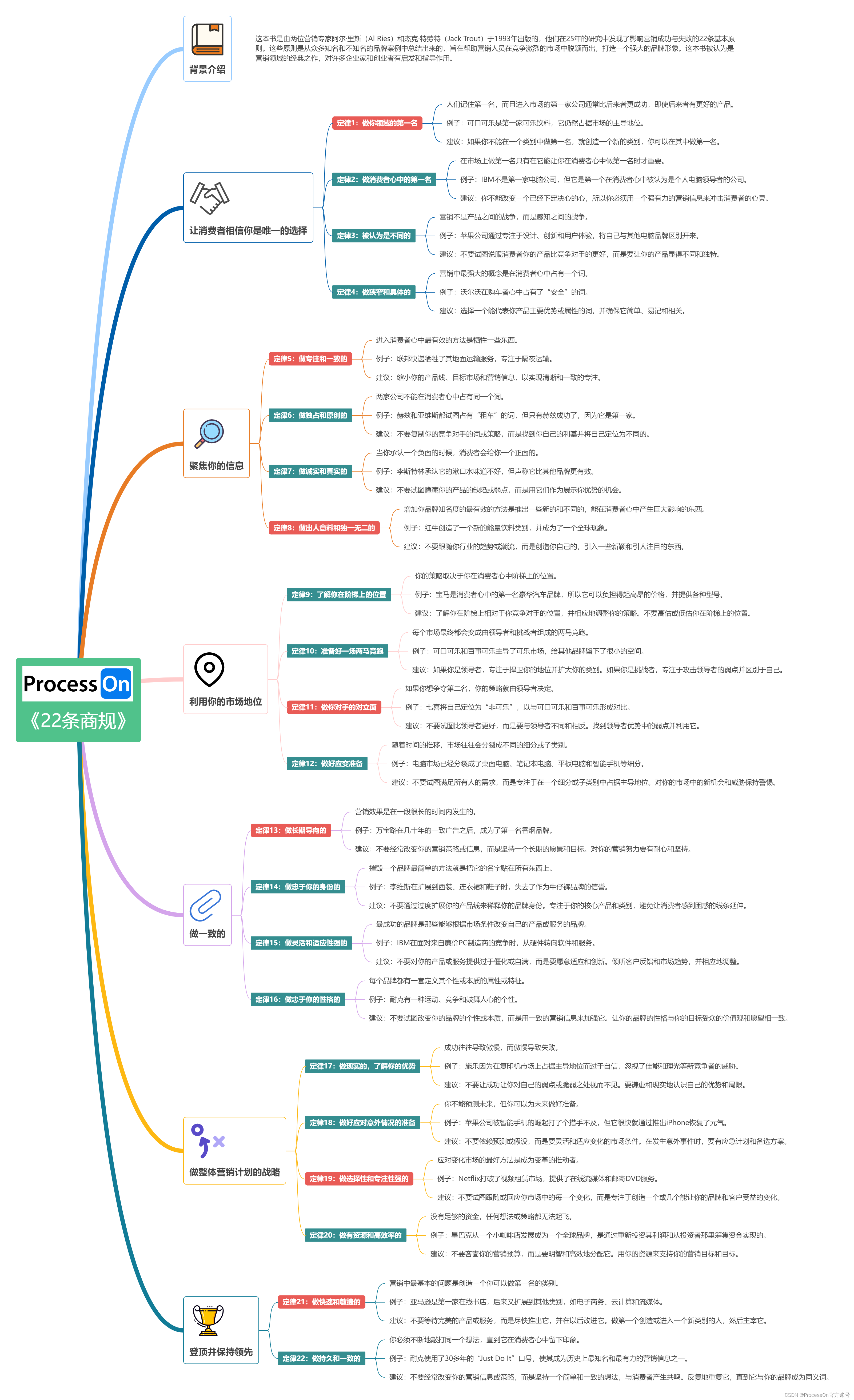
《22条商规》精简版
2、私域流量运营方案:瑞幸私域全案+实操,全流程深度拆解!

3、会议纪要

4、中国近代史纲要
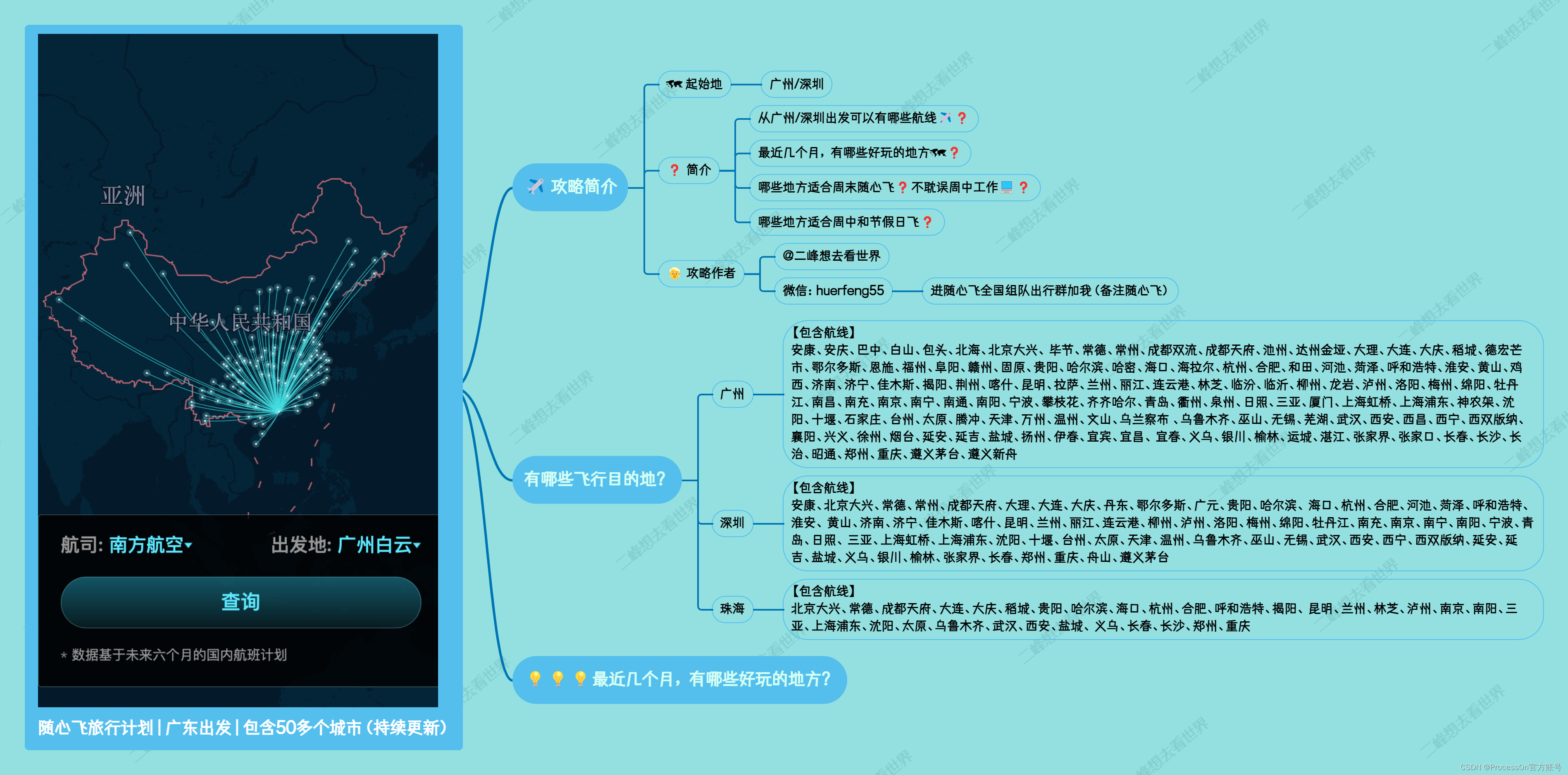
5、随心飞旅行计划 | 广东出发 | 包含50多个城市(持续更新)
6、2023苏州公司OKR

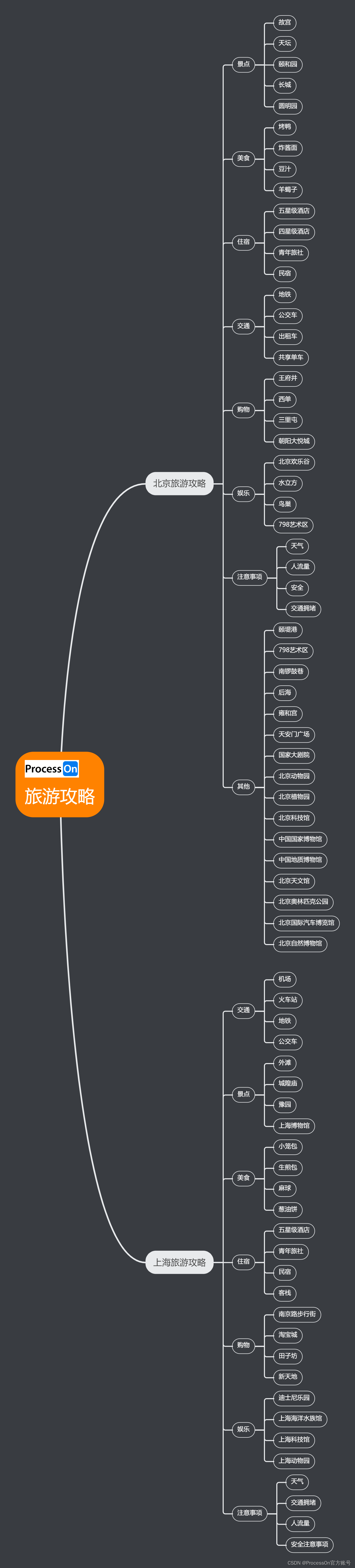
7、北京上海旅游攻略
8、 资产减值

9、ProcessOn模板社区-稻盛和夫给管理者的60个忠告

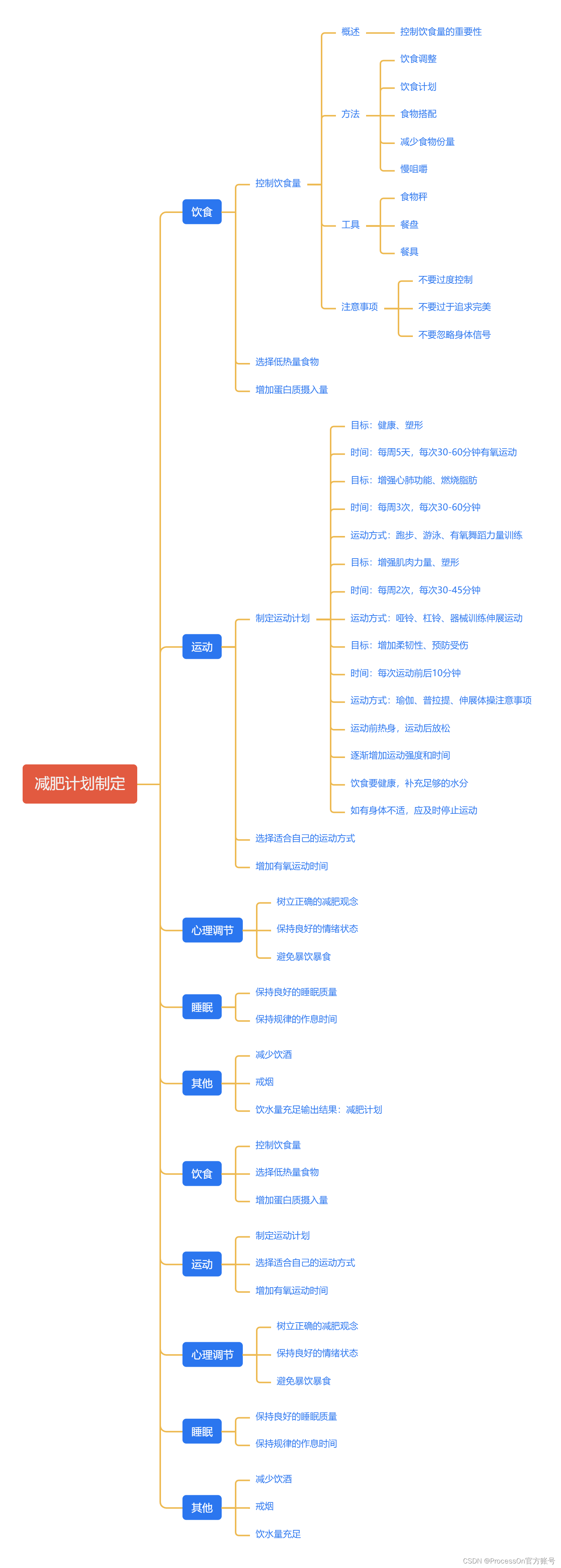
10、减肥计划
11、ProcessOn模板社区-B端产品

12、ProcessOn模板社区-《沟通的艺术》全书核心观点一览

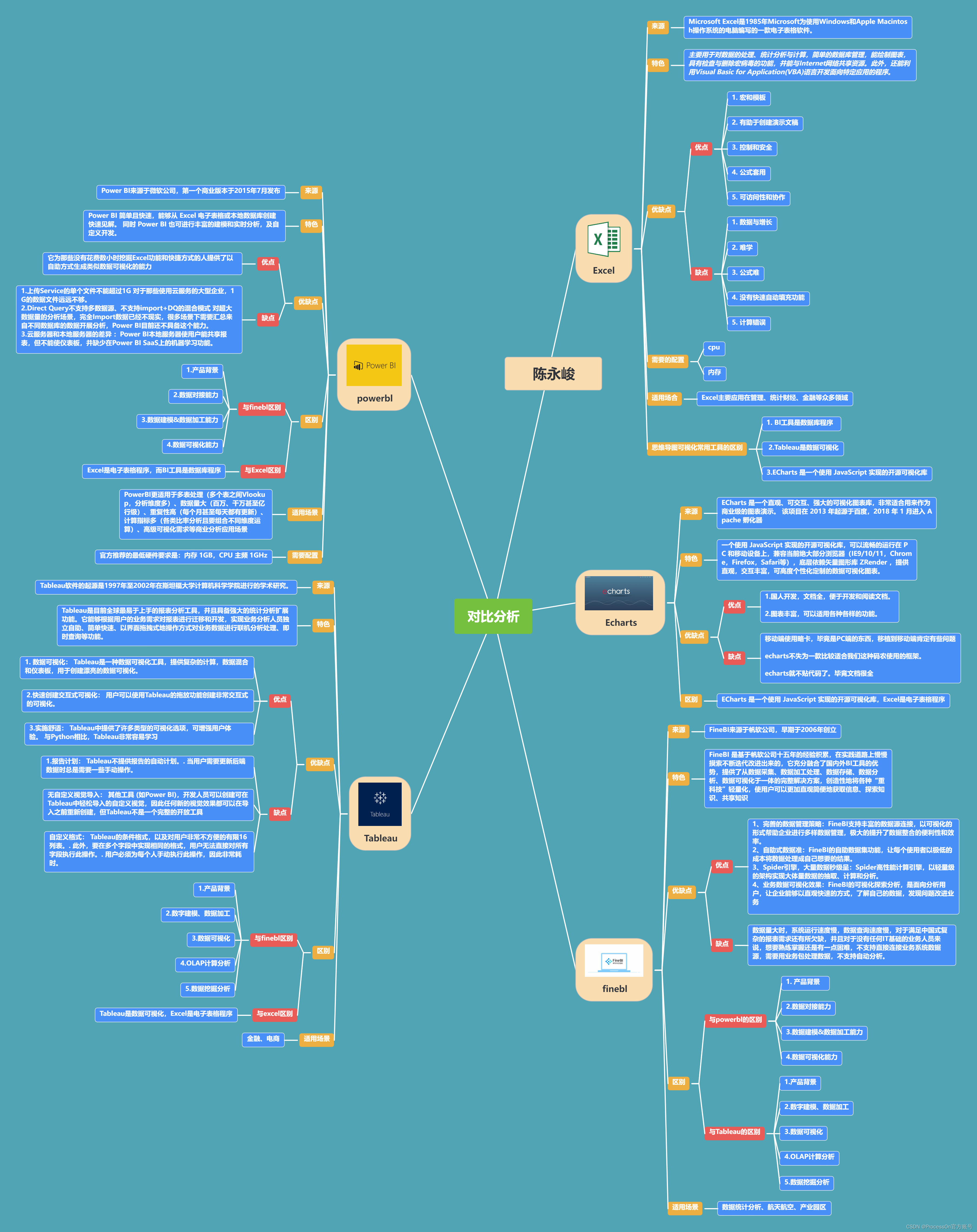
13、ProcessOn模板社区-对比分析 https://www.processon.com/view/6408156c91ff683bad8615ce#pc
14、中国古币简史

15、ProcessOn模板社区-《半小时漫画中国史(4)》全书思维导图 读书笔记

如果您对思维导图感兴趣,或者您觉得思维导图对您有作用。欢迎来ProcessOn 来体验 最酷的思维导图创作方式,AI+思维导图,让一切创作更加高效。
相关文章:

漂亮实用的15个脑图模板,你知道哪些是AI做的吗?
对于很多第一次接触到思维导图的朋友,看到软件的时候往往找不到方向,不知道如何创作? 今天大家的好助手来了。 一是有大量的思维导图模板,大家看着模板做,慢慢就会做了。 二是ProcessOn 思维导图已经可以用AI 做思维…...

历代程序员都无法逃脱的诅咒 -- 低代码
1764年5月4日星期四 愤怒的纺织工人 纵火烧毁了哈格里夫斯的家 因为他发明的珍妮纺织机 让很多当地的手工纺织工人失业了 这也被认为是第一次工业革命的开端 由于事发的星期四 所以这一事件也被称作疯狂星期四 类似的变革 也一次次的出现在软件行业 他是历代程序员都无法逃脱的…...

14Exceptional Control Flow Exceptions and Process(异常控制流,异常和进程)
异常控制流 异常控制流出现的地方: 异常控制流(Exceptional Control Flow,ECF)是程序执行过程中由于某些特殊事件或条件而导致的控制流的改变。异常控制流通常出现在以下几种情况: 硬件异常和中断:硬件异…...

LeetCode - 两数之和
题目信息 源地址:两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不…...

Python 小型项目大全 31~35
三十一、猜数字 原文:http://inventwithpython.com/bigbookpython/project31.html 猜数字是初学者练习基本编程技术的经典游戏。在这个游戏中,电脑会想到一个介于 1 到 100 之间的随机数。玩家有 10 次机会猜出数字。每次猜中后,电脑会告诉玩…...

他又赚了一万美金
有一些学员真的挺能干的,收了一万刀,感到欣慰,毕竟在国外lead这条路,有很多人被骗,也有很多人赚钱。 但是大部分人跟着某一些所谓的大佬,最后自己却不动手操作。 从一开始怕跟我学习,到最后选…...

企业工程项目管理系统+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

教你使用Apache搭建Http
Apache2默认采用的是80端口号,因此直接通过公网ip或域名就能访问。现实中,很多服务器本身就部署了许多其它服务,80端口号往往被占用,因此就需要将Apache2改成其它访问端口。 修改端口,首先需要修改/etc/apache2/ports…...
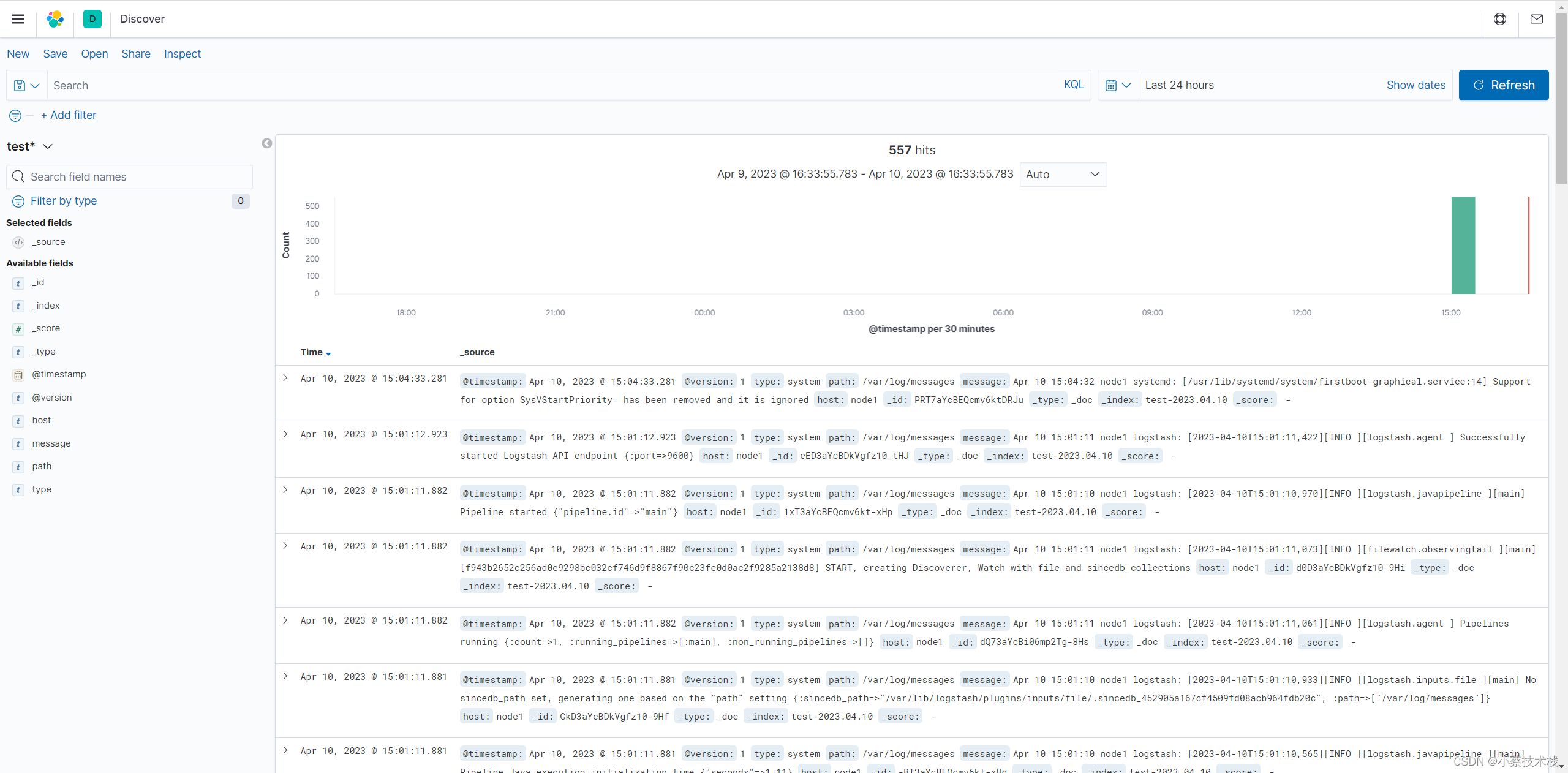
ZooKeeper+Kafka+ELK+Filebeat集群搭建实现大批量日志收集和展示
文章目录一、集群环境准备二、搭建 ZooKeeper 集群和配置三、搭建 Kafka 集群对接zk四、搭建 ES 集群和配置五、部署 Logstash 消费 Kafka数据写入至ES六、部署 Filebeat 收集日志七、安装 Kibana 展示日志信息一、集群环境准备 1.1 因为资源原因这里我就暂时先一台机器部署多…...

数据结构初阶 - 总结
-0- 数据结构前言 什么是数据结构 什么是算法 数据结构和算法的重要性-1- 时间复杂度和空间复杂度 👉数据结构 -1- 时间复杂度和空间复杂度 | C 算法效率 时间复杂度大O的渐进表示法eg 空间复杂度 常见复杂度对比OJ 消失的数组 轮转数组-2- 顺序表 与 链表 &am…...
)
代码随想录算法训练营第四十四天-动态规划6|518. 零钱兑换 II ,377. 组合总和 Ⅳ (遍历顺序决定是排列还是组合)
如果求组合数就是外层for循环遍历物品,内层for遍历背包。 如果求排列数就是外层for遍历背包,内层for循环遍历物品。 求物品可以重复使用时,最好是用一维数组,会比较方便。二维数组不想思考了,二维还是用在01背吧吧。…...
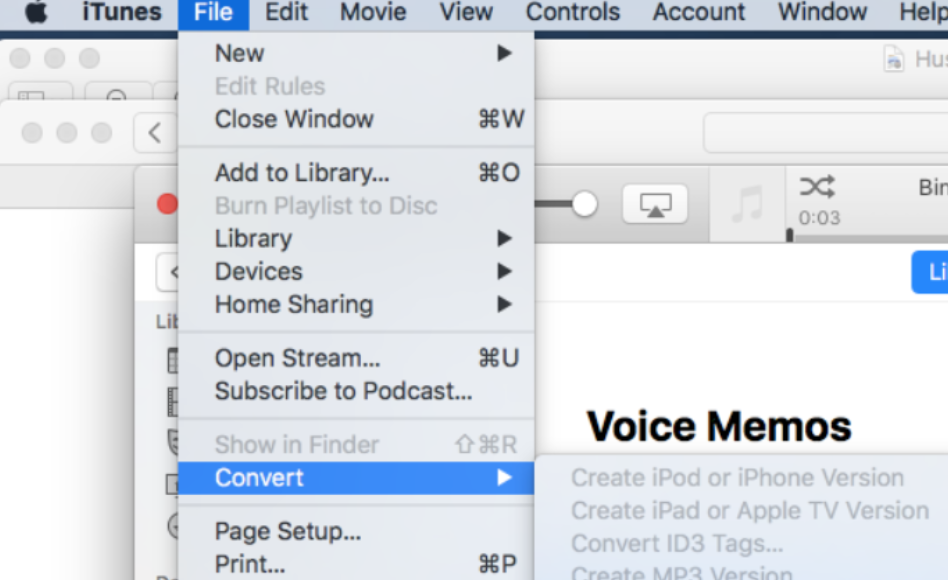
wma格式怎么转换mp3,4种方法超快学
其实我们在任何电子设备上所获取的音频文件都具有自己的格式,每种格式又对应着自己的属性特点。比如wma就是一种音质优于MP3的音频格式,虽然很多小伙伴比较青睐于wma所具有的音质效果,但也不得不去考虑因wma自身兼容性而引起很多播放器不能支…...
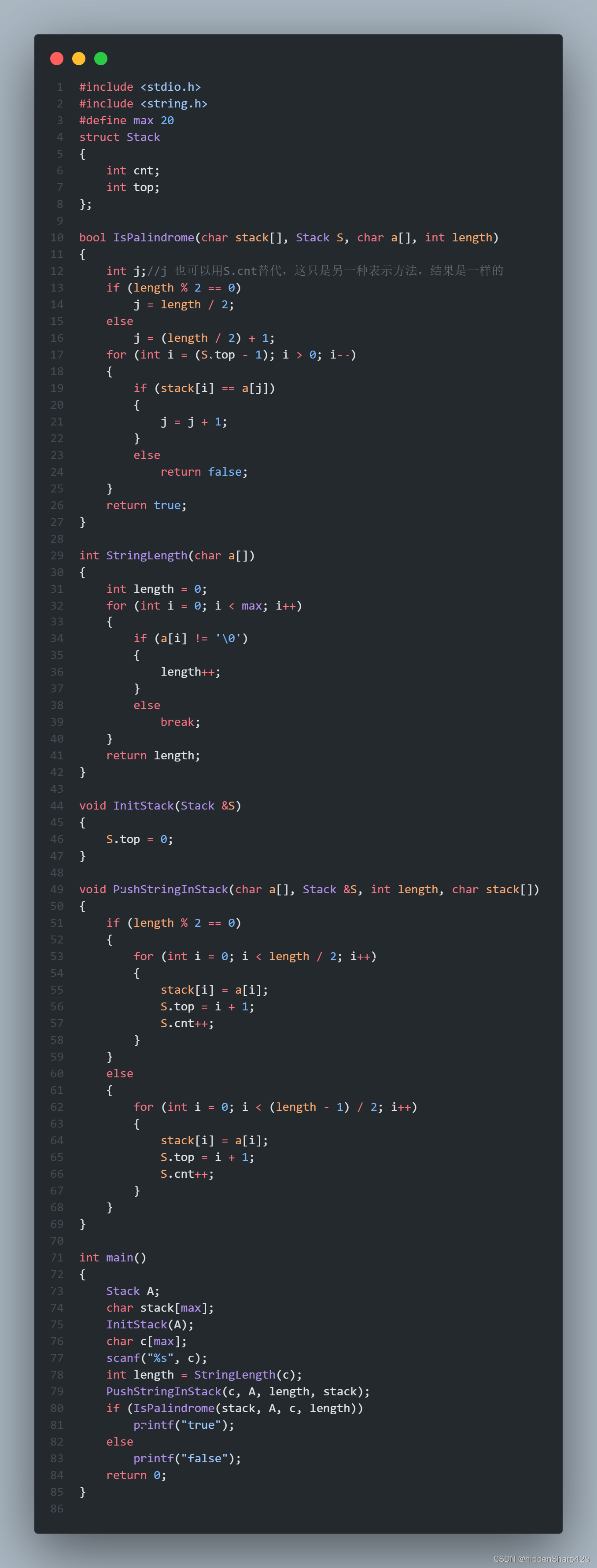
【数据结构与算法】判定给定的字符向量是否为回文算法
题目: Qestion: 试写一个算法判定给定的字符向量是否为回文。 回文解释: 回文是指正读反读均相同的字符序列,如“abba”和“abdba”均是回文,但“good”不是回文。 主要思路: 因为数据要求不是很严格并且是一个比较简单的…...
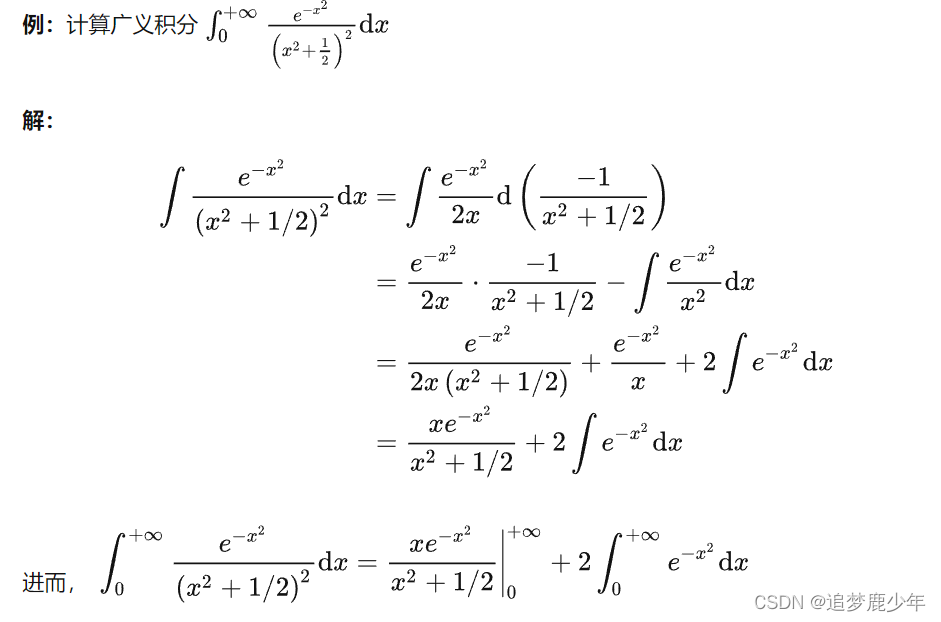
考研数二第十七讲 反常积分与反常积分之欧拉-泊松(Euler-Poisson)积分
反常积分 反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。 含有无穷上限/下…...
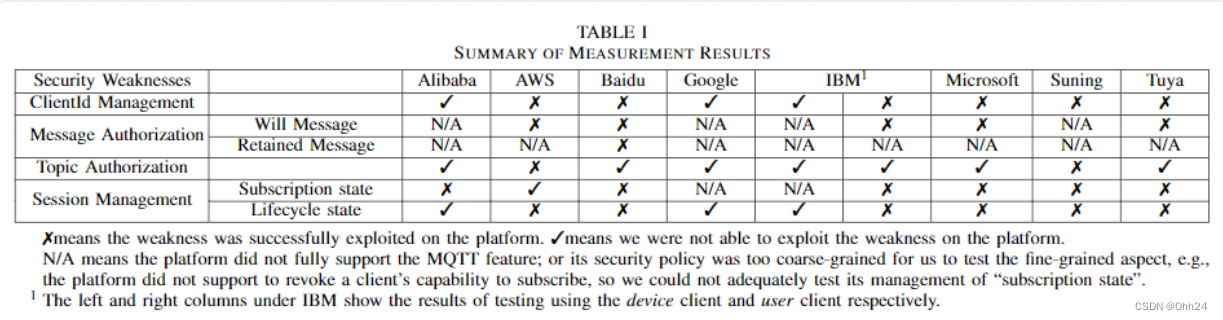
【论文总结】理解和减轻IoT消息协议的安全风险
理解和减轻IoT消息协议的安全风险介绍概述前置知识威胁模型MQTT IoT通信安全分析未授权的MQTT消息未授权的Will消息未经授权的保留消息MQTT会话管理故障未更新的会话订阅状态未更新的会话生命周期状态未经身份验证的 MQTT 身份客户端id劫持MQTT Topics的授权MQTT Topic不安全的…...

SpringBoot基础入门
一、概述 Spring Boot是一个开源的Java框架,它是基于Spring框架的基础之上创建的。Spring Boot可以帮助开发人员更快地创建Spring应用程序,并以最小的配置要求来运行它们。Spring Boot可以用于构建各种类型的应用程序,包括Web应用程序、RESTful API、批处理作业、消息传递应…...

jar 包与 war 包区别
1、war是一个web模块,其中需要包括WEB-INF,是可以直接运行的WEB模块;jar一般只是包括一些class文件,在声明了Main_class之后是可以用java命令运行的。 2、war包是做好一个web应用后,通常是网站,打成包部署…...

【数据结构:复杂度】时间复杂度
本节重点内容: 算法的复杂度时间复杂度的概念大O的渐进表示法常见时间复杂度计算举例⚡算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的&…...
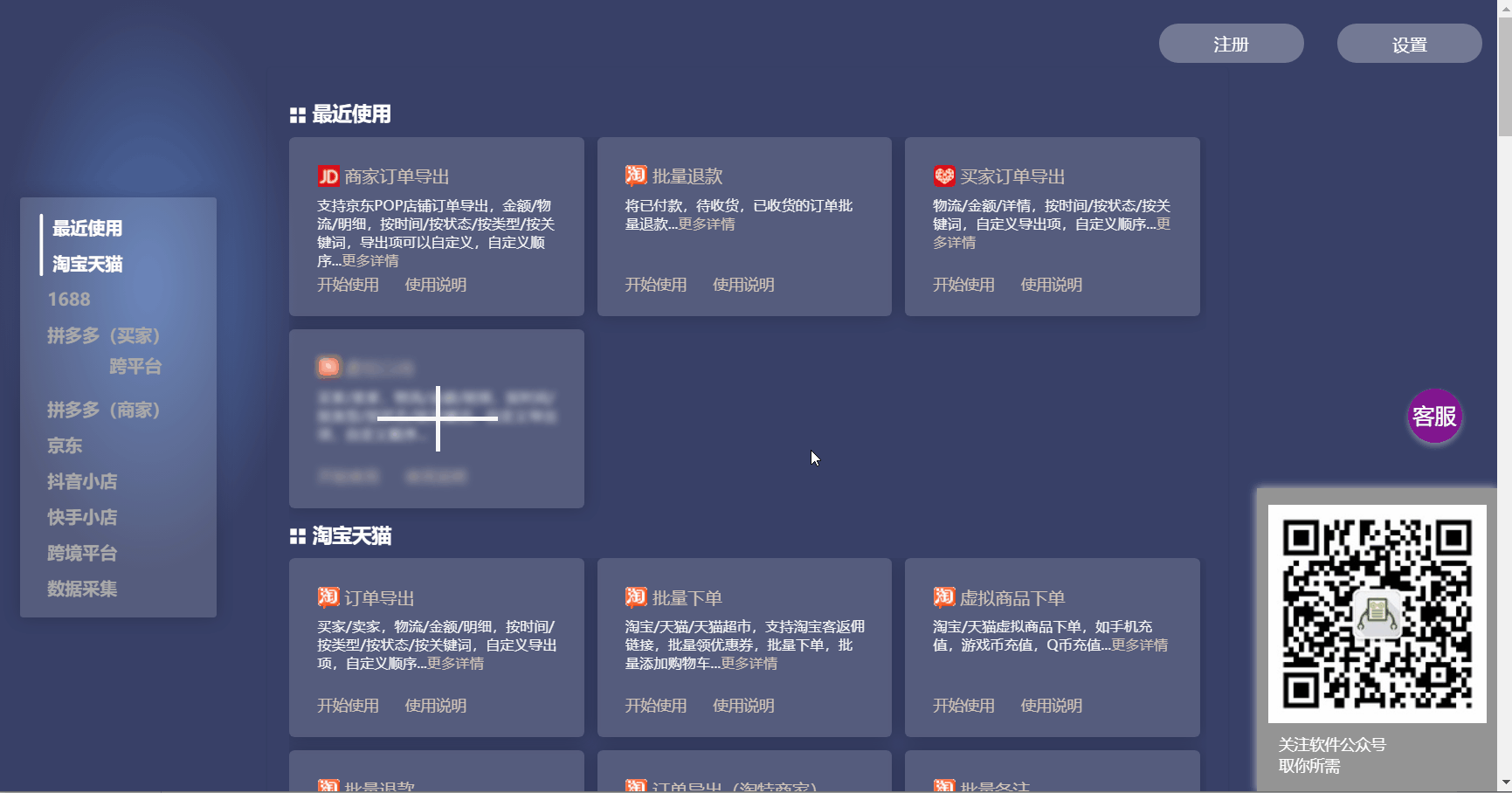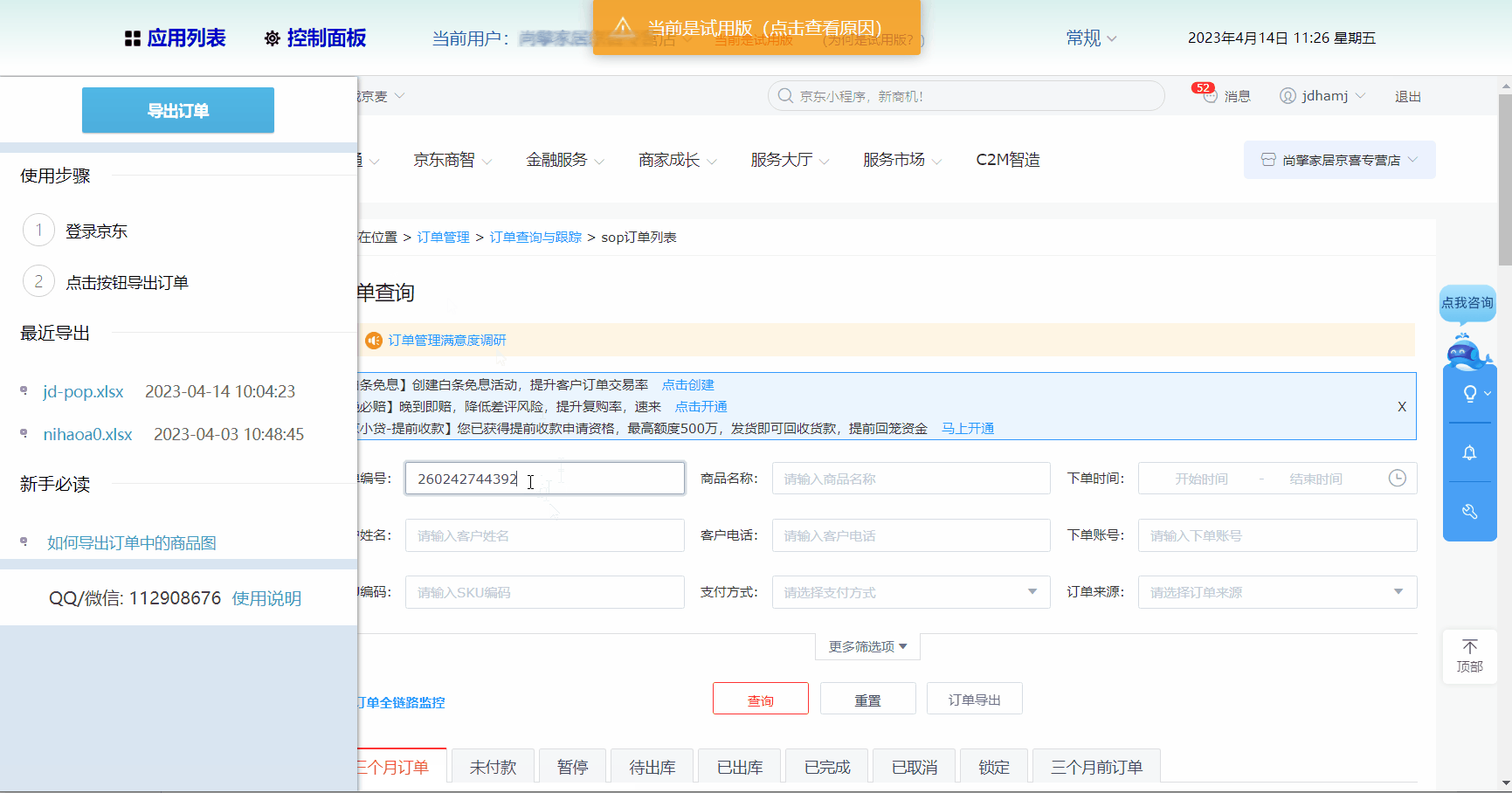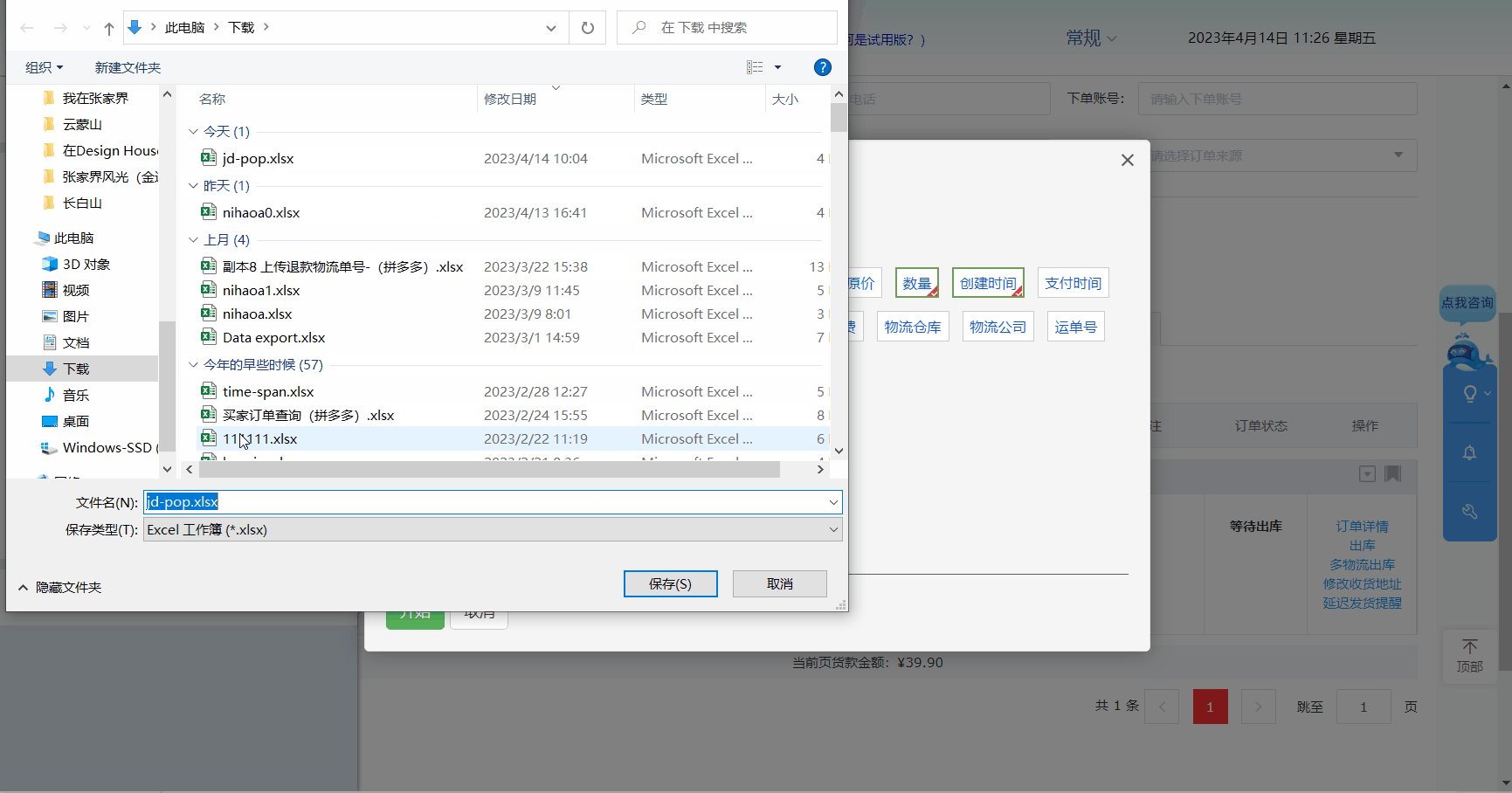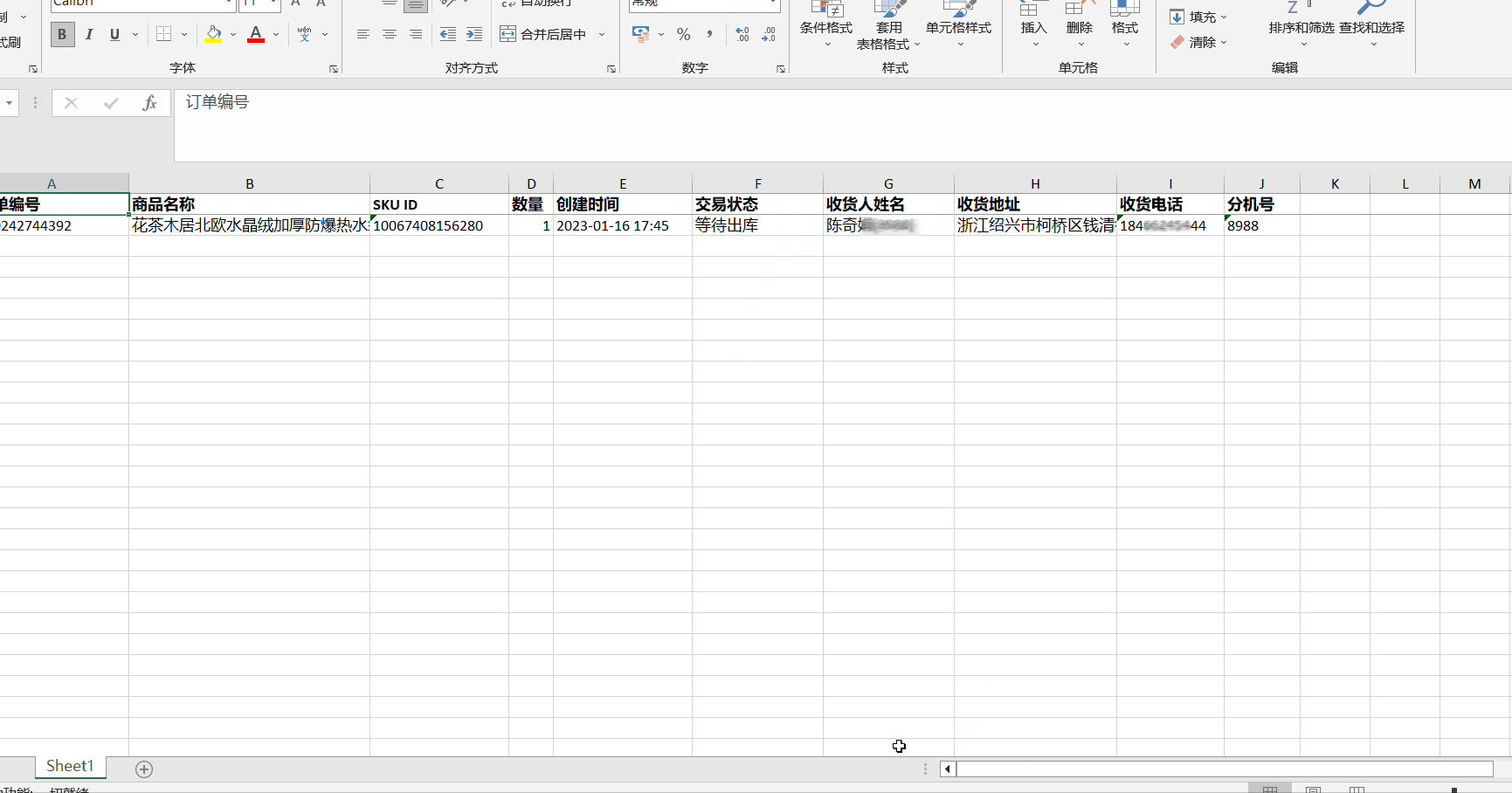
京东pop店铺订单导出
下载安装与运行 下载、安装与运行 语雀 特别提醒 只能导出已登录店铺的订单导出的收件人手机号是虚拟号 功能 主要是方便线下工厂发货的店主 所见即所得的导出自由选择导出项自由排序Excel导出列顺序导出过程中有进度提示,用户可以随时提前中止 什么是所见即所…...

论文阅读:Towards Stable Test-time Adaptation in Dynamic Wild World
今天阅读ICLR 2023 ——Towards Stable Test-time Adaptation in Dynamic Wild World Keywords:Test-time adaptation (TTA); 文章目录Towards Stable Test-time Adaptation in Dynamic Wild WorldProblem:motivation:Contributio…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
