考研数二第十七讲 反常积分与反常积分之欧拉-泊松(Euler-Poisson)积分
反常积分
反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。
含有无穷上限/下限的反常积分
看到“无穷”这两个字,我们第一时间想到这玩意肯定跟极限有关系。但是转念一想,我们都是对函数求极限啊,怎么对积分求极限呢?
不要急。牛顿——莱布尼茨公式可是可以把积分转化为函数的。这样不就可以对把这类反常积分转化为函数的极限问题了吗。

含有瑕点的反常积分
瑕点就是瑕疵点,即不完美的点,意思就是这个点让积分看起来“不完美”了。不过在数学上,瑕点特指邻域内无界的点。
前面的含有无穷限的积分是因为“无穷”不是一个数,不能被代入牛顿——莱布尼茨公式。那么问题来了,为什么有瑕点的积分要被列为反常积分呢?

那么如何处理含有瑕点的积分呢?很简单,既然瑕点会影响积分的结果,那就想办法避开瑕点,但在避开瑕点的时候有不能影响积分的值。
那我们很自然的就可以想到可以靠无限逼近瑕点来实现在尽可能不影响结果的情况下避开瑕点。具体要从哪一侧逼近,要具体分析,去看从哪一侧逼近可以避开瑕点。
既然出现了“无限”一词,肯定又要用到极限了。具体的就不细说了,直接看例题。

我们学了两种反常积分,一种是含有无穷积分限的,另一种是含有瑕点的。解决这两种反常积分的方法都是利用极限。关键所在就是要把对积分的极限转化为对牛顿——莱布尼茨公式的极限。
广义积分是否收敛





欧拉-泊松积分
欧拉-泊松 积分,又叫概率积分,在概率论中有着重要的应用。




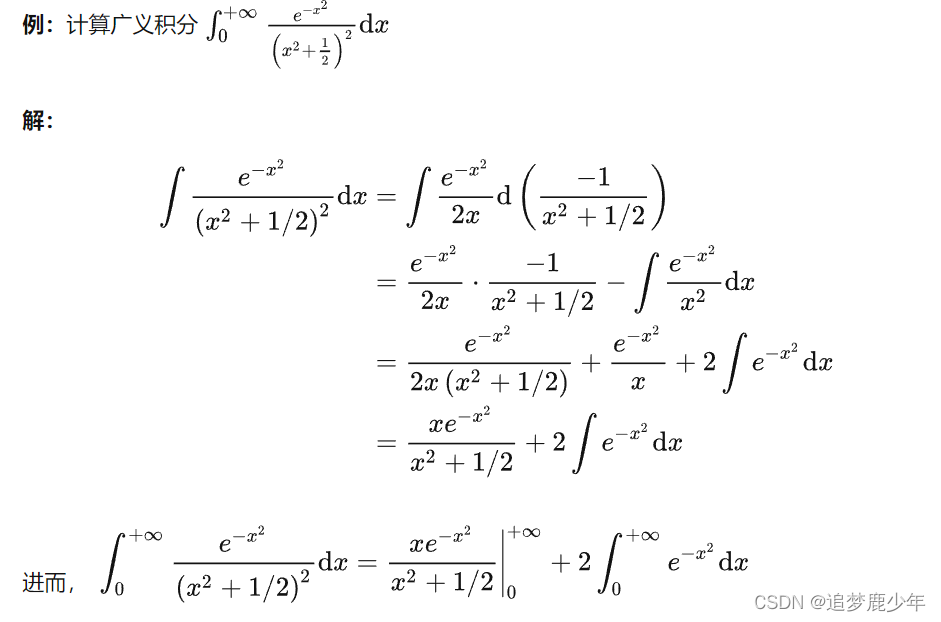
记一个方法:τ(1)=1,τ(12)=π,τ(n+1)=n∗τ(n)\tau (1)=1 , \tau(\frac{1}{2})=\sqrt{π} ,\tau(n+1)=n*\tau(n)τ(1)=1,τ(21)=π,τ(n+1)=n∗τ(n)
∫0∞t12.e−tdt=τ(12+1)\int_{0}^{∞} t^{\frac{1}{2}}.e-^t dt=\tau(\frac{1}{2}+1)∫0∞t21.e−tdt=τ(21+1)=12\frac{1}{2}21* τ(12)\tau(\frac{1}{2})τ(21)=12\frac{1}{2}21* π\sqrt{π}π
相关文章:
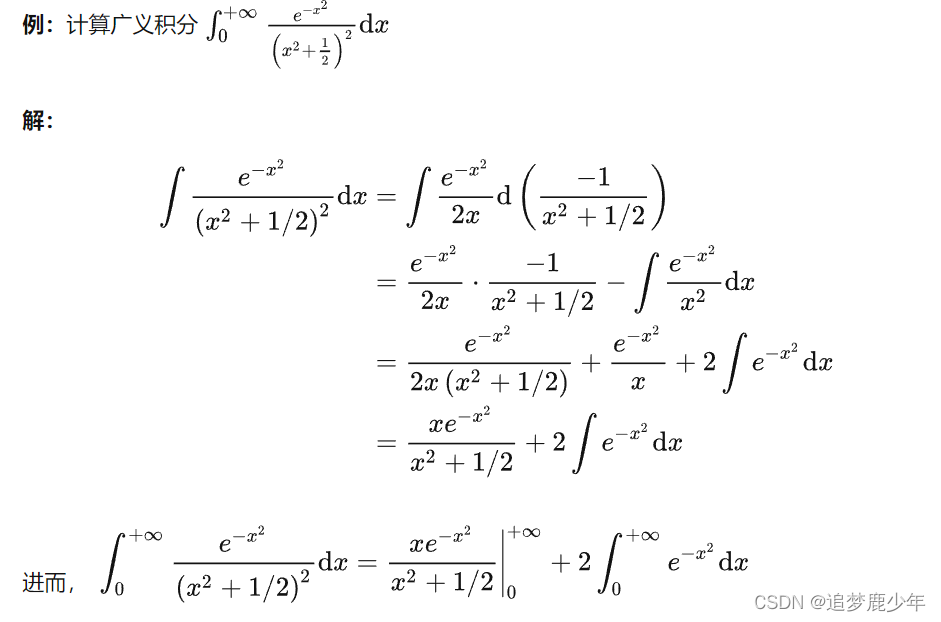
考研数二第十七讲 反常积分与反常积分之欧拉-泊松(Euler-Poisson)积分
反常积分 反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。 含有无穷上限/下…...
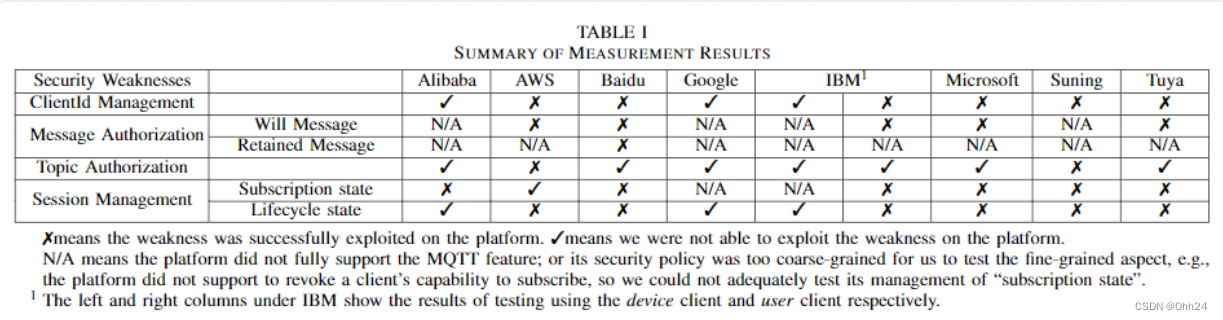
【论文总结】理解和减轻IoT消息协议的安全风险
理解和减轻IoT消息协议的安全风险介绍概述前置知识威胁模型MQTT IoT通信安全分析未授权的MQTT消息未授权的Will消息未经授权的保留消息MQTT会话管理故障未更新的会话订阅状态未更新的会话生命周期状态未经身份验证的 MQTT 身份客户端id劫持MQTT Topics的授权MQTT Topic不安全的…...

SpringBoot基础入门
一、概述 Spring Boot是一个开源的Java框架,它是基于Spring框架的基础之上创建的。Spring Boot可以帮助开发人员更快地创建Spring应用程序,并以最小的配置要求来运行它们。Spring Boot可以用于构建各种类型的应用程序,包括Web应用程序、RESTful API、批处理作业、消息传递应…...

jar 包与 war 包区别
1、war是一个web模块,其中需要包括WEB-INF,是可以直接运行的WEB模块;jar一般只是包括一些class文件,在声明了Main_class之后是可以用java命令运行的。 2、war包是做好一个web应用后,通常是网站,打成包部署…...

【数据结构:复杂度】时间复杂度
本节重点内容: 算法的复杂度时间复杂度的概念大O的渐进表示法常见时间复杂度计算举例⚡算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的&…...
京东pop店铺订单导出
下载安装与运行 下载、安装与运行 语雀 特别提醒 只能导出已登录店铺的订单导出的收件人手机号是虚拟号 功能 主要是方便线下工厂发货的店主 所见即所得的导出自由选择导出项自由排序Excel导出列顺序导出过程中有进度提示,用户可以随时提前中止 什么是所见即所…...

论文阅读:Towards Stable Test-time Adaptation in Dynamic Wild World
今天阅读ICLR 2023 ——Towards Stable Test-time Adaptation in Dynamic Wild World Keywords:Test-time adaptation (TTA); 文章目录Towards Stable Test-time Adaptation in Dynamic Wild WorldProblem:motivation:Contributio…...

2022国赛27:Linux-1时间服务chrony配置
大赛试题内容: 3.利用chrony配置Linux-1为其他Linux主机提供时间同步服务。 解答过程: 安装chrony服务[root@cs1 ~]# yum -y install chrony 配置/etc/chrony.conf文件[root@cs1 ~]# vi /etc/chrony.conf 7行改为 server 10.10.70.101 iburst 23行改为 去掉#号 allow 1…...
Java——二维数组中的查找
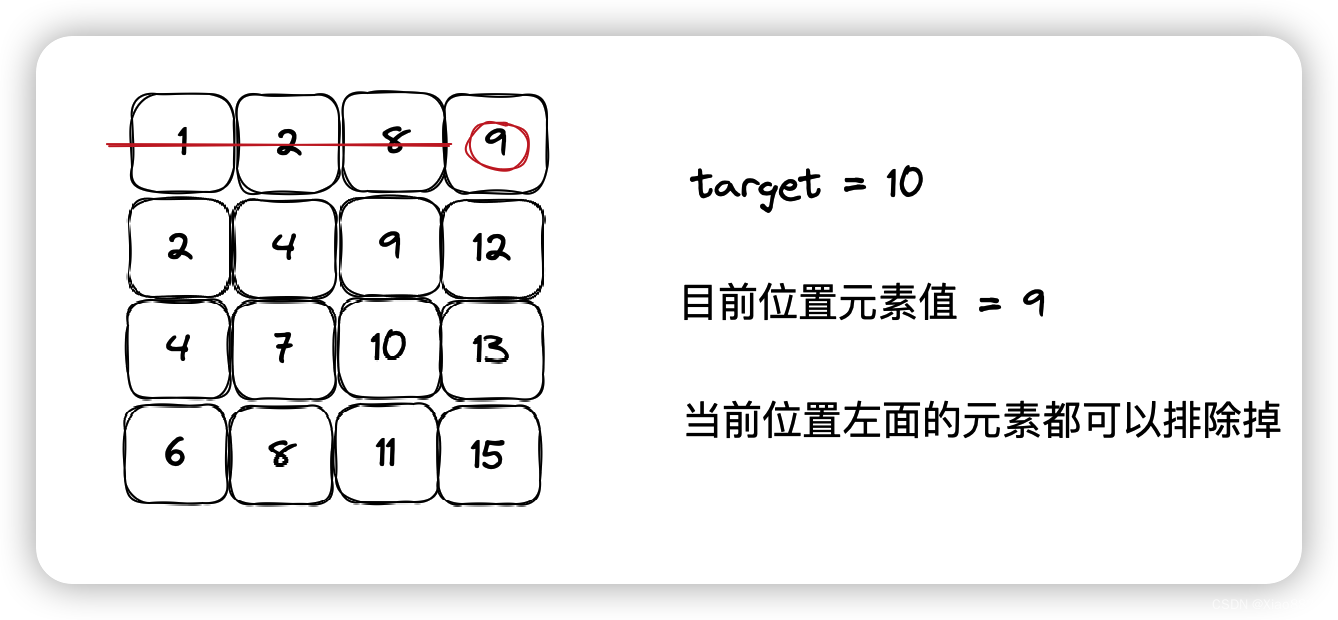
题目链接 牛客在线oj题——二维数组中的查找 题目描述 在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二…...

Android 9.0 添加关机铃声功能实现
1.前言 在9.0的系统rom定制化开发中,在原生系统中,关于开机铃声和关机铃声是默认不支持的,系统默认支持开机动画和关机动画等功能,所以关于增加开机铃声和关机 铃声的相关功能,需要自己增加相关的关机铃声功能 2.添加关机铃声功能实现的核心类 frameworks\base\cmds\boo…...

IPv4 和 IPv6 的组成结构和对比
IPv4 和 IPv6 的组成结构和对比IPv4IPv6互联网协议 (IP) 是互联网通信的基础,IP 地址是互联网上每个设备的唯一标识符。目前最常用的 IP 协议是 IPv4,它已经有近 30 年的历史了。然而,IPv4 存在一些问题,例如: 地址空间不足:IPv4 …...

Spring的事务管理
Spring的事务管理Spring的事务管理1、事务的回顾【1】事务的定义【2】事务的ACID原则2、spring事务API介绍【了解】【1】PlatformTransactionManager【1.1】PlatformTransactionManager作用【1.2】PlatformTransactionManager接口【1.3】PlatformTransactionManager实现类【2】…...
:VADC驱动配置详解(理论基础篇))
MCAL知识点(十六):VADC驱动配置详解(理论基础篇)
目录 1、概述 2、EB配置 2.1、通用界面配置 2.1.1、General 2.1.2、AdcConfigSet_0 2.1.3、AdcGlobinputClass 2.1.4、AdcHwUn...
MySQL--库的操作--校验规则对于数据库的影响--0409
目录 1.库的基础操作 查看数据库 创建数据库 删除数据库 查看建库语句 修改数据库 2.字符集和字符集校验规则 2.1 查看系统默认字符集以及校验规则 2.2 使用特定的字符集创建数据库 2.3 不同校验规则对数据库的影响 2.3.1 大小写验证 2.3.2 排序验证 3.备份和恢复 3.1…...
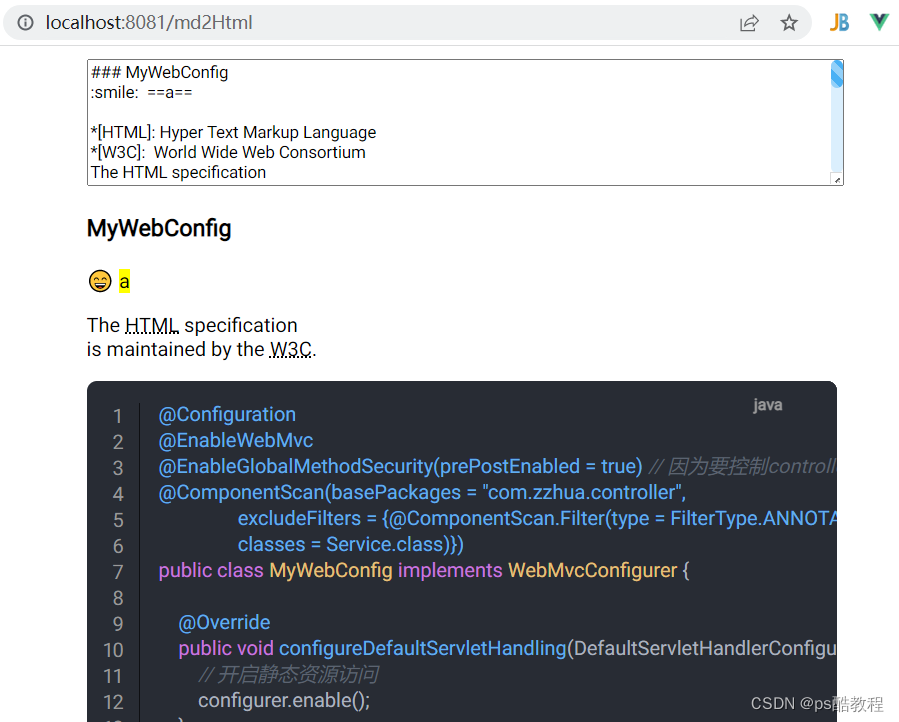
markdown-it基本使用
markdown-it能够将markdown语法的内容转换为html内容,这样我们使用markdown语法写的笔记,就可以转换作为网页使用了 Markdown语法 Markdown语法图文全面详解(10分钟学会) 基础使用 安装markdown-it npm install markdown-it --save使用markdown-it …...

CMake入门教程【核心篇】8.3对象库
文章目录 知识点实例代码目录代码实现知识点 add_library(libhello OBJECT src/hello.cpp)使用OBJECT 参数可以把对象传入到libhello 中,且不会生成.lib文件 使用变量$<TARGET_OBJECTS:libhello>即可获取,比较实用 实例 代码目录 |-📁prj10 |-- 🎴CMakeLists…...
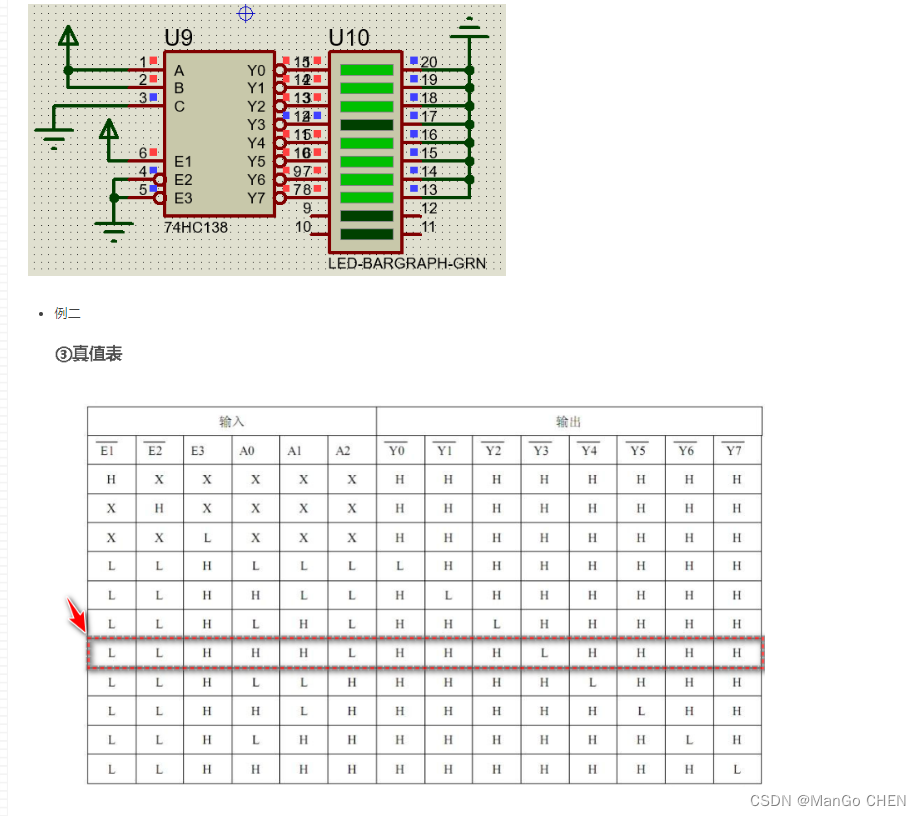
单片机_CT107D训练平台电路原理图\蓝桥杯训练板\IO扩展模块\74HC138译码器
74HC138译码器(实现3个IO口控制8个引脚实现IO口的扩展) 配置信号放大模块,可以对输入的低电压模拟信号进行放大; 配置 138 译码器,可以做译码实验; 外设可以用存储器映射方式访问,也可以直接控…...

Rabbitmq消息确认机制
1.生产者确认机制 确认消息发送到交换机--Confirm方式 1.1普通Confirm方式 private static void sendMsg(Channel channel) throws IOException, InterruptedException { //开启确认机制 channel.confirmSelect(); //发送消息到exchange St…...
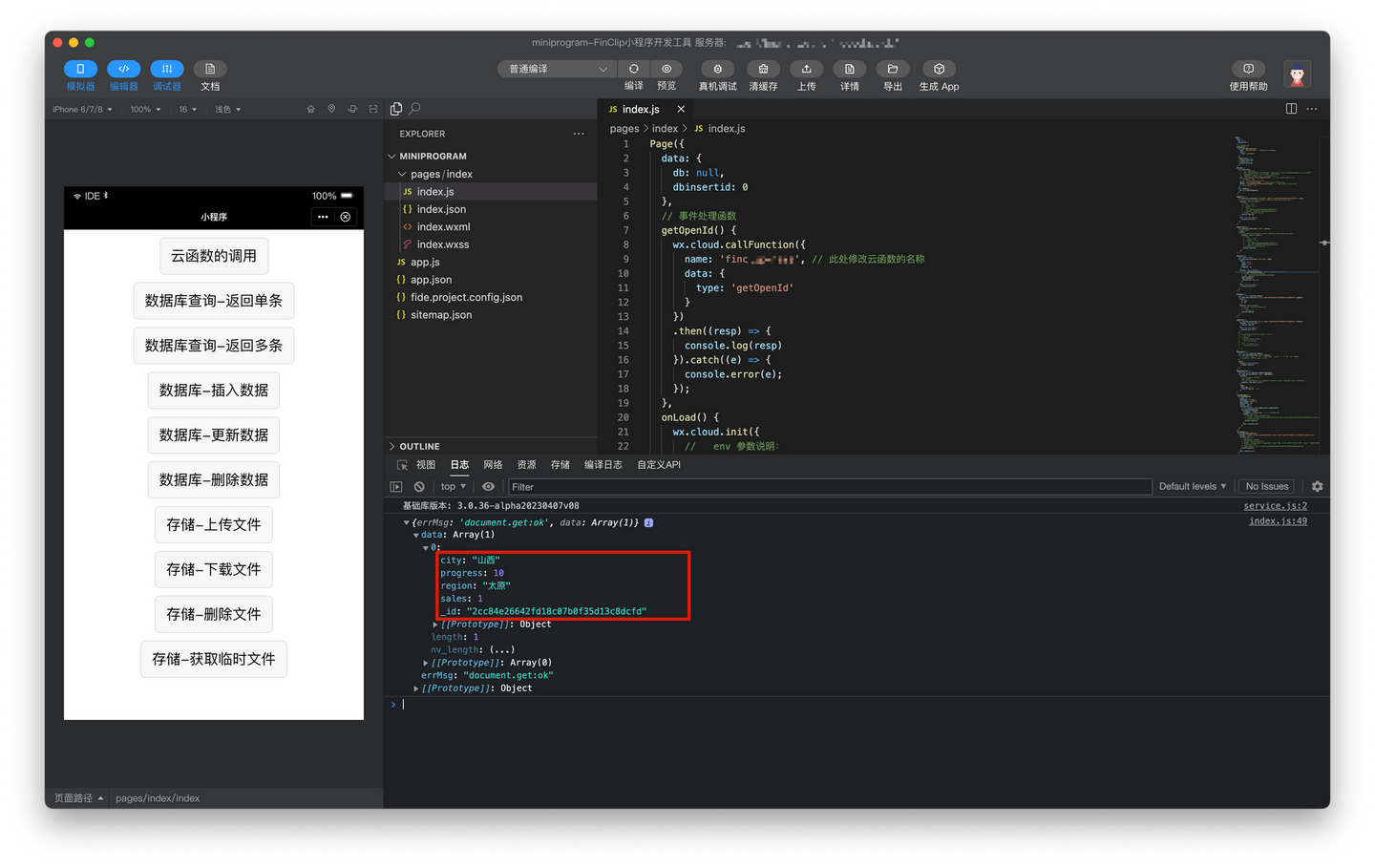
FinClip 云开发实践(附小程序demo)
在开发一个小程序时,除了考虑界面功能逻辑外,还需要后端的数据支持,开发者需要提前考虑服务器、存储和数据库等相关需求的支持能力,此外还可能需要花费时间精力在部署应用、和依赖服务的建设上。 因此,腾讯小程序为…...

真正好用的工业品ERP系统应该是什么样的?
一个好用的进销存ERP系统应该有以下特点: 1. 全面覆盖企业经营流程,包括采购、销售、库存、财务等模块,能够实现全方位的管理和控制。 2. 自定义配置,灵活地适应大多数用户的需求。 3. 数据精准、实时化,支持统计分…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
