2022年第十三届蓝桥杯题解(全)C/C++

A题就是一个简单的进制转化,代码实现如下:
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int main()
{int x = 2022;int a = 1;int res = 0;while(x) {res += (x % 10) * a;a = a * 9;x /= 10;}cout << res;return 0;
}
B题有很大的争议,我认为顺子的意思是从0开始的至少为三个数的升序序列。那这样的话答案就是:14

C题是一个很普通的思维题,先记录一下每周能做多少题,然后统计一下总的做题数除以每周能做的题然后乘以7,再加上从周一开始计算每一天什么时候能大于这个总的题数的天数即可。
#include <bits/stdc++.h>using namespace std;
typedef long long LL;const int N = 1e5 + 10;int main()
{LL a, b, n, t, res;cin >> a >> b >> n;t = a * 5 + b * 2;res = n / t * 7;n %= t;if(n > 0)for(int i = 1; i <= 7; i ++ ){if(i == 6 || i == 7) n -= b;else n -= a;res ++;if(n <= 0) break;}cout << res;return 0;
}
D题应该是最简单的一道,开一个n的数组a[i],a[i]表示每一个灌木能长得最大高度,最大高度等于它右侧的树木数乘以2;
#include <bits/stdc++.h>using namespace std;
typedef long long LL;const int N = 1e4 + 10;int a[N], n;int main()
{cin >> n;for(int i = 1; i <= (n + 1) / 2; i ++ ) {a[i] = (n - i) * 2;a[n - i + 1] = a[i];}for(int i = 1; i <= n; i ++ ) {cout << a[i];if(i != n) cout << "\n";}return 0;
}

E题就开始有点意思了,这道题是一个简单贪心,重点在于读题(其实接触过这个进制问题的童鞋应该一样就看懂了emmm)。
我们先分析一下题干的65是怎么出来的:第一数位每一个数代表的必然是1,第二数位是由第一数位的二进制晋上来的,所以第二数位每一个数代表的是2,第三数位是由第二数位十进制进位上来的,所以第三数位每一个数代表的是2 * 10 = 20,所以这个x(321) = 3 * 20 + 2 * 2 + 1 * 1 = 65;
题目的意思是保证x(a) >= x(b) , 求两个数的差值最小。显然对于每一数位,其进制越小,两个数的后一数位做差所得到的值越小,所以每一数位最小的合法进制数就行。
#include <bits/stdc++.h>
#define int long longusing namespace std;const int mod = 1e9 + 7, N = 1e5 + 10;int a[N], b[N];
int ma, mb, n;signed main()
{cin >> n;cin >> ma;for(int i = 1; i <= ma; i ++ ) cin >> a[i];for(int i = 1; i <= ma / 2; i ++ ) swap(a[i], a[ma - i + 1]);cin >> mb;for(int i = 1; i <= mb; i ++ ) cin >> b[i];for(int i = 1; i <= mb / 2; i ++ ) swap(b[i], b[mb - i + 1]); int t = 1, ans = 0;//枚举每个数位for(int i = 1; i <= ma; i ++ ) {//当前数位贪心最优的进制 int z = max(a[i], b[i]) + 1;if(z < 2) z = 2; ans += a[i] * t - b[i] * t;ans %= mod;t = t * z % mod;}cout << ans;return 0;
}

F题可以暴力写一下,求一个前缀和,然后枚举子矩阵,时间复杂度是O(n^4), 显然过不了;
这个题考的是一个双指针,枚举一下矩阵中的左右边界,在每一个左右边界中,从上往下求一下子段中小于等于k的数的数量(用双指针扫一下就可以,这一步可以做到o(n));
时间复杂度:O(n ^ 3)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include <bits/stdc++.h>using namespace std;const int N = 510;
typedef long long LL;int a[N][N];int main()
{int n, m, k;scanf("%d%d%d", &n, &m, &k);for(int i = 1; i <= n; i ++ )for(int j = 1; j <= m; j ++ )scanf("%d", &a[i][j]);for(int i = 1; i <= n; i ++ )for(int j = 1; j <= m; j ++ )a[i][j] += a[i][j - 1];LL cnt = 0;for(int i = 1; i <= m; i ++ )for(int j = i; j <= m; j ++ ) {int res = 0;for(int l = 1, r = 1; r <= n; r ++ ) {res += a[r][j] - a[r][i - 1];while(res > k && l <= r) {res -= a[l][j] - a[l][i - 1];l ++;}if(res <= k && l <= r) cnt += r - l + 1;} }printf("%lld", cnt);return 0;
}
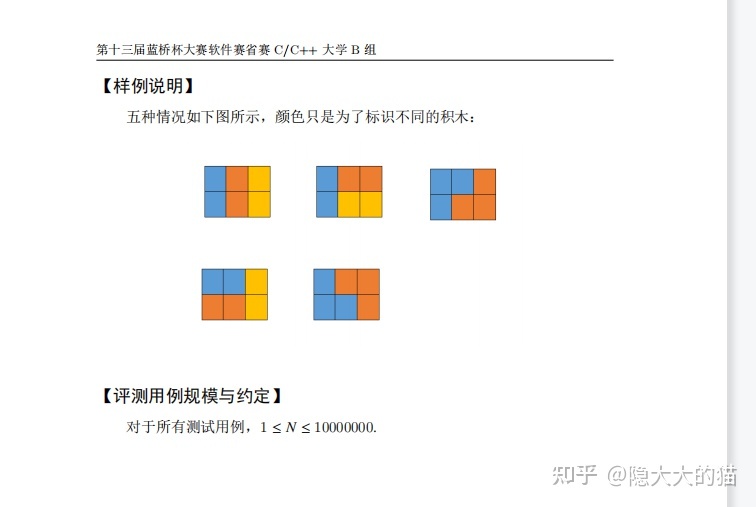
这个题考的是一个dp;
状态表示: f[i][j]表示前i列积木中,第i列状态为j的情况数。
四种情况:j = 0, 表示当前列为空, 1表示当前列上面有一个格子,2表示当前列下面有一个格子,3表示当前列已满。
由于数据很大,开一个4e8的空间会爆,可以用p来表示上一层状态,q来表示当前层的状态,类似于背包的滚动数组优化。
状态转移看一下代码吧,我感觉还是比较好理解的,不懂的可以评论区问我
#include <bits/stdc++.h>using namespace std;
typedef long long LL; const int N = 1e7 + 10, mod = 1e9 + 7;LL p[4], q[4];int main()
{int n;cin >> n;p[3] = 1;for(int i = 1; i <= n; i ++ ) {q[3] = (p[0] + p[1] + p[2] + p[3]) % mod;q[0] = p[3] % mod;q[1] = (p[0] + p[2]) % mod;q[2] = (p[0] + p[1]) % mod;for(int i = 0; i <= 3; i ++ )p[i] = q[i];}cout << p[3];return 0;
}

ps:题不可以用并查集去做,因为雷的爆炸是由方向的,A雷爆炸可以引爆B雷,但是B雷爆炸是有可能无法引爆B雷的(爆炸半径不同)
ps:我补题的时候被卡常卡了一天,最后把idx.find改成idx.count就过了(emm55555)
正解是dfs,为了避免边被卡成O(n * n), 以至于tle,我们就需要去除重复的点,记录每一个坐标下点的位置.
然后把每一个火箭作为根节点,去遍历周围r ^ 2的雷,统计一下一共能炸多少雷就可以。
O(100 * n + m)最坏情况为每一个雷有100条边;
#pragma GCC optimize(2)
#include <bits/stdc++.h>using namespace std;
typedef long long LL;const int N = 2e5 + 10;struct Node {int x, y, r, l;
}a[N];
//x,y到下标的映射
unordered_map<LL, int> idx;
bool st[N];
int n, m, cnt;
int ans;LL cal(int x, int y) {return (LL)x * (1000000000 + 1) + y;
}bool solve(int x, int y, int r) {if(x * x + y * y <= r * r) return true;else return false;
}void dfs(int i)
{//标记当前点st[i] = true;//加上当前点雷的数量ans += a[i].l;int r = a[i].r;//printf("%d %d %d\n", a[i].x, a[i].y, a[i].r);//遍历当前点周围是否有没遍历的子节点,有的话继续dfsfor(int x = max(a[i].x - r, 0); x <= min(a[i].x + r, 1000000000); x ++ ) {for(int y = max(a[i].y - r, 0); y <= min(a[i].y + r, 1000000000); y ++ ) {if(solve(x - a[i].x, y - a[i].y, r)) {LL xy = cal(x, y);if(idx.count(xy)) {int u = idx[xy];if(!st[u]) {dfs(u);//printf("%d\n", u);}}}}}}int main()
{scanf("%d%d", &n, &m);for(int i = 1; i <= n; i ++ ) {int x, y, r;scanf("%d%d%d", &x, &y, &r);LL xy = cal(x, y);//如果没有这个点if(idx.find(xy) == idx.end()) {//将这个点存入idx数组idx[xy] = ++cnt; //将这个点存入a数组a[cnt] = {x, y, r, 1};}else {int u = idx[xy];//这个点已经存在并且半径更大,则会更新这个以前点的编号下的r的值a[u].r = max(a[u].r, r);//这个点的出现次数加一++ a[u].l;}//int u = idx[xy];//printf("%d %d %d %d\n", a[u].x, a[u].y, a[u].r, a[u].l);}for(int i = 1; i <= m; i ++ ) {int x, y, r;scanf("%d%d%d", &x, &y, &r);//将这个点加入a中作为起始点,去搜一下其他的雷a[cnt + 1] = {x, y, r};dfs(cnt + 1);}printf("%d", ans);return 0;
}

I题又是一个dp,这个dp感觉比上面那个简单一点;
状态表示:f[i][j][k]表示访问前i个位置时,恰好访问j个店并且酒量恰好为k的时候的方案数;
准确来说这个做法并不能维护所有前i个位置恰好访问j个店的方案数,但是题目只问最后一次遇到花且恰好把酒喝光的次数,所以对于大于100的酒量的状态就不用转移了,因为在后面接近100个位置中,全看花也不能把酒喝完。
状态转移; 看花 : f[i][j][k] = f[i - 1][j][k + 1] 遇店 : f[i][j][k] = f[i - 1][j - 1][k / 2];//注意边界!不要越界
#include <bits/stdc++.h>using namespace std;const int N = 110, mod = 1e9 + 7;//前i次访问,访问j个店的酒量是多少
long long f[N * 2][N][110];int main()
{int n, m;scanf("%d%d", &n, &m);f[0][0][2] = 1;for(int i = 1; i < n + m; i ++ )for(int j = 0; j <= n; j ++ )for(int k = 0; k <= 100; k ++ ) {f[i][j][k] = (f[i][j][k] + f[i - 1][j][k + 1]) % mod;if((k % 2 == 0) && j) f[i][j][k] = (f[i][j][k] + f[i - 1][j - 1][k / 2]) % mod;}printf("%lld", f[n + m - 1][n][1]);return 0;
}


这个题有两个做法,一种是用set或者堆来维护一个高度到区间的映射,另一个用并查集维护区间,这个做法我没做出来,我用了两个set来做,果然被卡常了.
正解:这个题本质是一个最长公共下降子序列的问题,对于任意一个h,只要它高度降到了与前一个高度下降过程中的公共值,那么它就不需要花费代价继续下降。如果它降得的当前高度与前一个高度没有公共值,则需要多花费一个代价,来降低自己的高度。我们只需要开两个数组暴力做一下就行。
时间复杂度: O(n);
#include <bits/stdc++.h>using namespace std;
typedef long long LL;const int N = 2e5 + 10;LL a[N];
vector<LL> b[N];
int n;LL solve(LL x) {return sqrt(x / 2 + 1);
}int main() {scanf("%d", &n);for(int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);int res = 0;for(int i = 1; i <= n; i ++ ) {while(a[i] > 1) {int flag = 0;for(LL j : b[i - 1]) {if(a[i] == j) {flag = 1;break;}}if(!flag) res ++;b[i].push_back(a[i]);a[i] = solve(a[i]);}}printf("%d", res);return 0;
}相关文章:

2022年第十三届蓝桥杯题解(全)C/C++
A题就是一个简单的进制转化,代码实现如下: #include <bits/stdc.h>using namespace std;const int N 1e5 10;int main() {int x 2022;int a 1;int res 0;while(x) {res (x % 10) * a;a a * 9;x / 10;}cout << res;return 0; } B题有…...

【cmake学习】find_package 详解
find_package 主要用于查找指定的 package,主要支持两种搜索方法: Config mode:查找 xxx-config.cmake或 xxxConfig.cmake的文件,如OpenCV库的OpenCVConfig.cmakeModule mode:查找Findxxx.cmake文件,如Ope…...
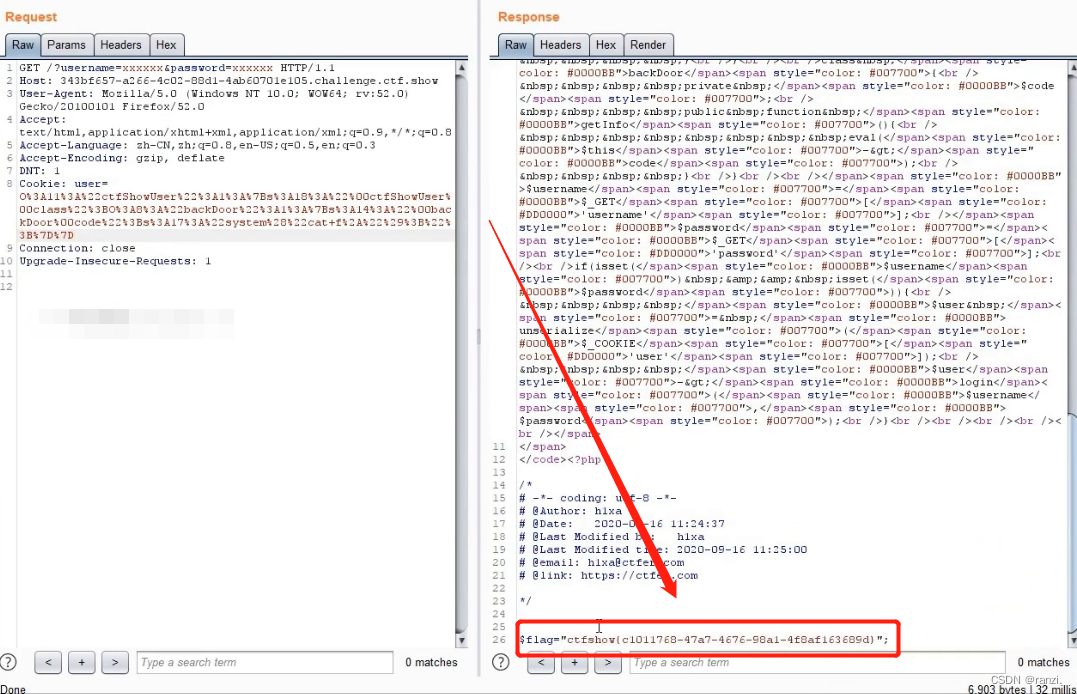
WEB攻防-通用漏洞PHP反序列化POP链构造魔术方法原生类
目录 一、序列化和反序列化 二、为什么会出现反序列化漏洞 三、序列化和反序列化演示 <演示一> <演示二> <演示二> 四、漏洞出现演示 <演示一> <演示二> 四、ctfshow靶场真题实操 <真题一> <真题二> <真题三> &l…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK里的图像处理库进行图像转换(C++)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK进行图像转换(C)Baumer工业相机Baumer工业相机的SDK里图像格式转换的技术背景Baumer工业相机通过BGAPI SDK进行图像转换调用BGAPI SDK的图像转换库ImageProcessor调用BGAPI SDK建立图像调用BGAPI SDK转换图像…...
, 获得店铺的所有商品,获取推荐商品列表, 获取购买到的商品订单列表))
JD开放平台接口(获得JD商品详情, 按关键字搜索商品,按图搜索京东商品(拍立淘), 获得店铺的所有商品,获取推荐商品列表, 获取购买到的商品订单列表)
参数说明 通用参数说明 url说明 https://api-gw.onebound.cn/平台/API类型/ 平台:淘宝,京东等, API类型:[item_search,item_get,item_search_shop等]version:API版本key:调用key,测试key:test_api_keysecret:调用secret,测试secret:(不用填写…...
上海亚商投顾:沪指震荡反弹 游戏、传媒概念股再度大涨
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪大小指数今日走势分化,沪指向上震荡反弹,创业板指一度跌近1%,黄白二线大幅背离。…...

C/C++ 玩转StoneValley库:从入门到精通
C/C 玩转StoneValley库:从入门到精通引言(Introduction)StoneValley库简介(Overview of StoneValley Library)为什么要学习StoneValley库(Why Learn StoneValley Library in C)StoneValley库安装…...
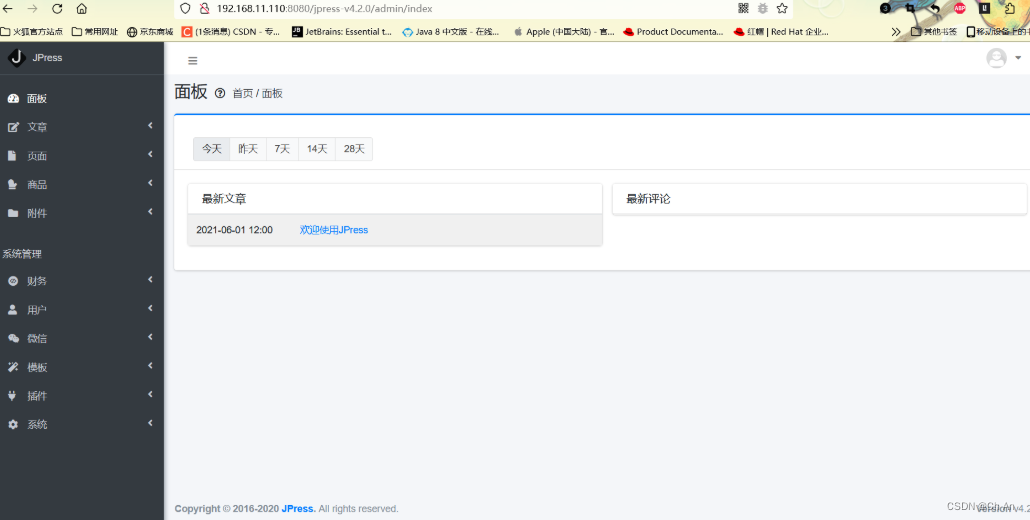
CentOS7-部署Tomcat并运行Jpress
1. 简述静态网页和动态网页的区别。 2. 简述 Webl.0 和 Web2.0 的区别。 3. 安装tomcat8,配置服务启动脚本,部署jpress应用。1、简述静态网页和动态网页的区别 静态网页: 请求响应信息,发给客户端进行处理,由浏览器进…...

菜鸟程序员的3年心酸逆袭之旅!今天你对我爱搭不理,明天我让你高攀不起!
多年前我以一个菜鸟的身份 进入了一家创业公司 我原本以为公司是这样的 但是实际上是这样的 我进去时 我们部门除开部门老大还有我 也只有我 所以我就这样开始了我的程序员生涯 开始了我的苦逼技术 公司是做电商网站的 因为我是一个菜鸟 所以我接到的第一个任务 就是做一个网页…...

【Scala】异常 隐式转换 泛型
目录 异常 隐式转换 隐式函数 隐式参数 隐式类 隐式解析机制 泛型 泛型上下限 上下文限定 来源: 异常 def main(args: Array[String]): Unit {try {var n 10 / 0}catch {case ex: ArithmeticException>{// 发生算术异常println("发生算术异常&quo…...

1673_MIT 6.828 Homework xv6 lazy page allocation要求翻译
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 在计划表中看到了这样一份作业,做一个简单的翻译整理。原来的页面:Homework: xv6 lazy page allocation (mit.edu) 家庭作业:x…...

六、Locust之TaskSets详解
TaskSets是一种结构化测试分层网站/系统的方法。你可以在这里阅读更多关于它的信息。 1.TaskSet class 如果你正在对一个以分层方式构建的网站进行性能测试,有章节和子章节,以同样的方式构建你的负载测试可能是有用的。 为了这个目的&#x…...

flask_知识点3_css
flask_知识点3_css样式1高度和宽度2行内和块级3字体和颜色4文字对齐方式5浮动6 内边距6 外边距!css重点1、css样式2、分析页面布局3、参考别人的成果css引用方式1 在标签上(不建议使用)// An highlighted block var foo bar;2 在head标签中写…...

Redis_概述_特性_IO模型
本章要点 掌握NoSql数据库的概念和与sql数据库的区别初步了解Redis内存数据库了解Redis内存数据库的优点及其原因掌握Redis的多线程IO模型学习Redis的安装和配置 Redis简介 Redis 全称 Remote Dictionary Server 远程字典服务! 使用C语言编写,支持网络,可基于内存也可以持久化…...

[论文速览] Sparks of Artificial General Intelligence: Early experiments with GPT-4
Sparks of Artificial General Intelligence: Early experiments with GPT-4 2023.3.22 微软官方发布了目前人类史上最强AI模型 GPT-4 的综合能力评估论文,总所周知,2023年是通用人工智能(Artificial General Intelligence,AGI&a…...

舔狗日记:学姐生日快到了,使用Python把她的照片做成视频当礼物
舔狗日记1前言一、需要调入的模块二、实现合并多张图片转成 mp4 视频三、优化改进一下总结前言 这不是学姐生日快到了,于是我学了一手使用Python来把学姐的照片生成为视频,到时候给她一个惊喜! 好了先不舔了,下面分享一下用pytho…...
收集使用个人信息自评估指南》看个人信息保护着力点)
从《移动互联网应用程序(App)收集使用个人信息自评估指南》看个人信息保护着力点
为指导应用运营者对自身收集、使用个人信息行为进行自查自纠,2019年3月,应用专项治理工作组发布了《应用违法违规收集使用行为自查自查指南》。个人信息”。随着对App违法收集、使用个人信息行为评价工作的开展和深入,《App违法违规收集、使用…...

电脑0x0000001A蓝屏错误怎么U盘重装系统教学
电脑0x0000001A蓝屏错误怎么U盘重装系统教学分享。有用户电脑开机之后遇到了系统蓝屏的情况。系统蓝屏问题很多时候都是系统bug,只有通过重装系统来进行解决。那么蓝屏问题如何通过U盘重装新系统来解决呢?来看看以下的详细操作方法教学吧。 准备工作&…...
Day939.如何小步安全地升级数据库框架 -系统重构实战
如何小步安全地升级数据库框架 Hi,我是阿昌,今天学习记录的是关于如何小步安全地升级数据库框架的内容。 当消息组件的数据存储都是采用 SQL 拼写的方式来操作,这样不便于后续的扩展及维护。除此之外,相比前面的其他重构&#x…...
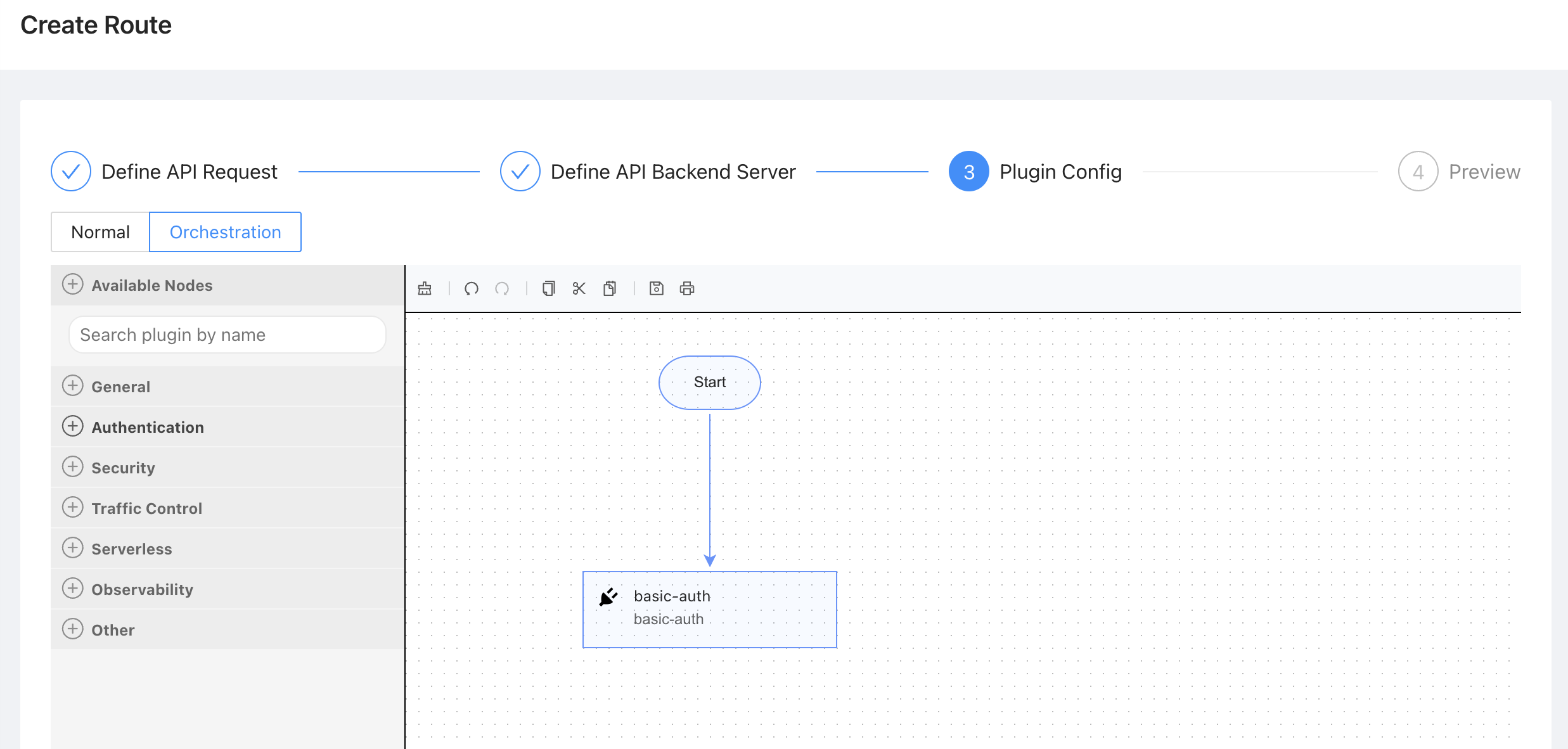
2023 年十大 API 管理趋势
作者郑玩星,API7.ai 技术工程师。 阅读原文 什么是 API?什么是 API 管理? 近期,AIGC(AI Generated Content,生成式人工智能)在各行业的应用日趋普及。AIGC 服务提供商通过 API 向外部提供其内…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
