算法总结-深度优先遍历和广度优先遍历
深度优先遍历(Depth First Search,简称DFS) 与广度优先遍历(Breath First Search,简称BFS)是图论中两种非常重要的算法,生产上广泛用于拓扑排序,寻路(走迷宫),搜索引擎,爬虫等。
一、深度优先遍历
深度优先遍历的思路是从图的一个未访问的顶点V开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底,不断递归重复此过程…直到所有的顶点都遍历完成。它的特点说通俗了就是不撞南墙不回头,走完了一条路,再换一条路继续走。
树是图的一种特例( 联通无环的图就是树),接下来我们来看树用深度优先遍历该怎么遍历。
1、深度优先遍历过程
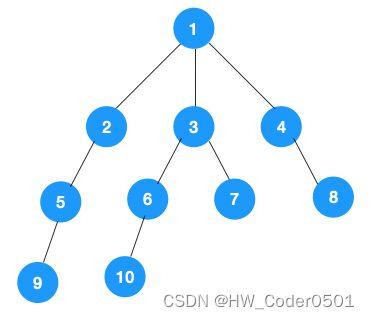
(1)、我们从根节点1开始深度优先遍历,它相邻的节点有2、3、4,依先遍历节点2,再遍历2的右边节点5,再遍历9,至此便无可遍历的节点。
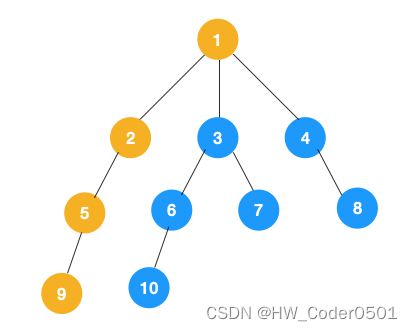
(2)、上图中一条路径已经遍历到底,此时从叶子节点9回退到上一节点5,,看下节点 5 是否还有除 9 以外的节点,没有继续回退到 2,2 也没有除 5 以外的节点,回退到 1,1 有除 2 以外的节点 3,所以从节点 3 开始进行深度优先遍历,如下:
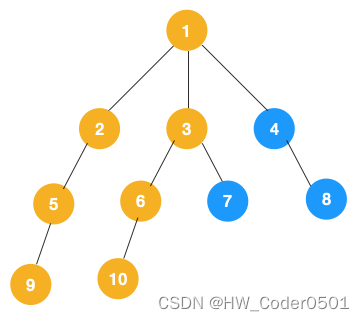
(3)、同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点,再往上回溯,发现3有除 6 以外的子节点 7,所以此时会遍历 7。
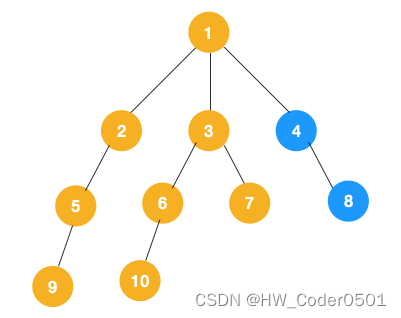
(4)、从 7 往上回溯到 3, 1,发现 1 还有节点 4 未遍历,所以此时沿着 4, 8 进行遍历,这样就完成了整个遍历过程。
完整的节点的遍历顺序如下(节点上的的蓝色数字代表):
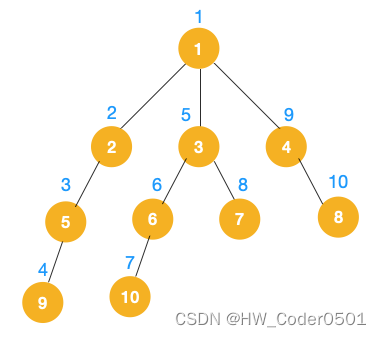
相信大家看到以上的遍历不难发现这就是树的前序遍历,实际上不管是前序遍历,还是中序遍历,亦或是后序遍历,都属于深度优先遍历。
那么深度优先遍历该怎么实现呢,有递归和非递归两种表现形式,接下来我们以二叉树为例来看下如何分别用递归和非递归来实现深度优先遍历。
2、深度优先遍历实现
(1)、递归
递归实现比较简单,由于是前序遍历,所以我们依次遍历当前节点,左节点,右节点即可,对于左右节点来说,依次遍历它们的左右节点即可,依此不断递归下去,直到叶节点(递归终止条件),代码如下:
public class Solution { private static class Node { public int value; // 节点值public Node left; // 左节点 public Node right; // 右节点public Node(int value, Node left, Node right) { this.value = value; this.left = left; this.right = right; } } public static void dfs(Node treeNode) { if (treeNode == null) { return; } process(treeNode); // 遍历节点dfs(treeNode.left); // 遍历左节点dfs(treeNode.right); // 遍历右节点}
}
递归的表达性很好,也很容易理解,不过如果层级过深,很容易导致栈溢出。所以我们重点看下非递归实现。
(2)、非递归
仔细观察深度优先遍历的特点,对二叉树来说,由于是先序遍历(先遍历当前节点,再遍历左节点,再遍历右节点),所以我们有如下思路:
对于每个节点来说,先遍历当前节点,然后把右节点压栈,再压左节点(这样弹栈的时候会先拿到左节点遍历,符合深度优先遍历要求)。
弹栈,拿到栈顶的节点,如果节点不为空,重复步骤 1, 如果为空,结束遍历。
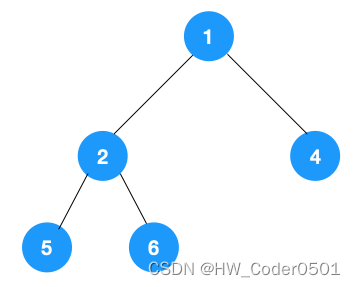
我们以以下二叉树为例来看下如何用栈来实现 DFS。
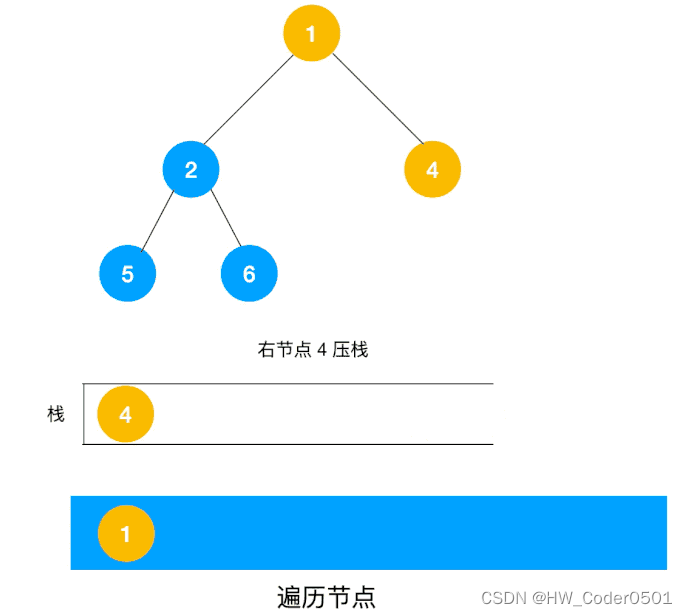
使用栈来将要遍历的节点压栈,然后出栈后检查此节点是否还有未遍历的节点,有的话压栈,没有的话不断回溯(出栈),有了思路,不难写出如下用栈实现的二叉树的深度优先遍历代码:
/** * 使用栈来实现 dfs * @param root */
public static void dfsWithStack(Node root) { if (root == null) { return; } Stack<Node> stack = new Stack<>(); // 先把根节点压栈 stack.push(root); while (!stack.isEmpty()) { Node treeNode = stack.pop(); // 遍历节点 process(treeNode) // 先压右节点 if (treeNode.right != null) { stack.push(treeNode.right); } // 再压左节点 if (treeNode.left != null) { stack.push(treeNode.left); } }
}
二、深度优先遍历
广度优先遍历,指的是从图的一个未遍历的节点出发,先遍历这个节点的相邻节点,再依次遍历每个相邻节点的相邻节点。
上面所述树的广度优先遍历动图如下,每个节点的值即为它们的遍历顺序。所以广度优先遍历也叫层序遍历,先遍历第一层(节点 1),再遍历第二层(节点 2,3,4),第三层(5,6,7,8),第四层(9,10)。
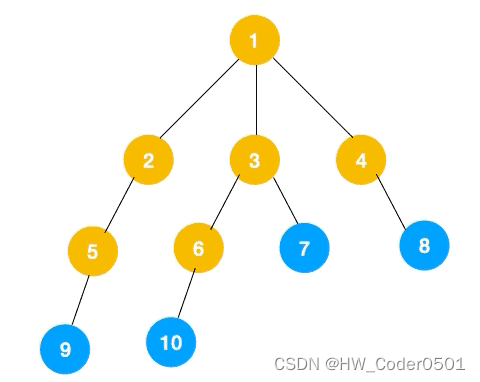
深度优先遍历用的是栈,而广度优先遍历要用队列来实现,我们以下图二叉树为例来看看如何用队列来实现广度优先遍历。
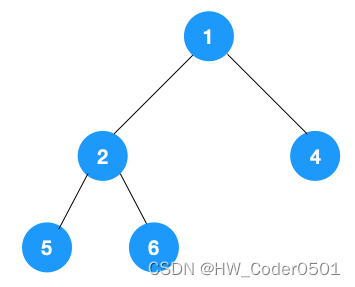
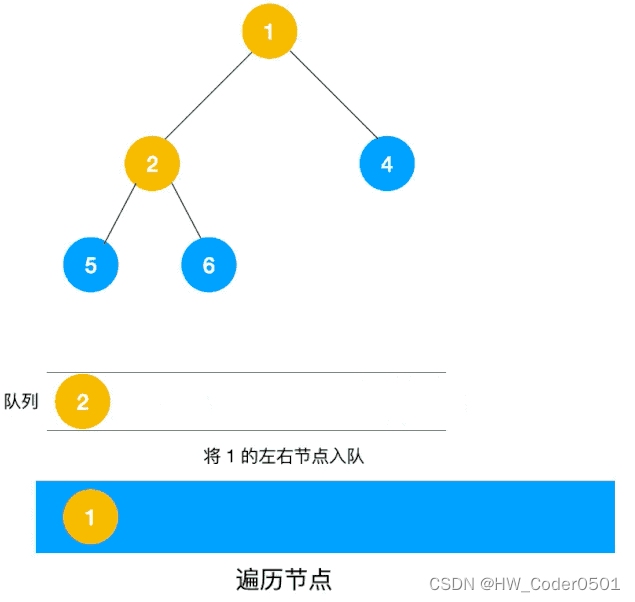
代码实现如下:
/** * 使用队列实现 bfs * @param root */
private static void bfs(Node root) { if (root == null) { return; } Queue<Node> stack = new LinkedList<>(); stack.add(root); while (!stack.isEmpty()) { Node node = stack.poll(); System.out.println("value = " + node.value); Node left = node.left; if (left != null) { stack.add(left); } Node right = node.right; if (right != null) { stack.add(right); } }
}
若想通过实战来进一步理解DFS,BFS,可以看LeetCode如下题目,这是一道典型的DFS,BFS题目。
leetcode 104,111: 给定一个二叉树,找出其最大/最小深度。
相关文章:

算法总结-深度优先遍历和广度优先遍历
深度优先遍历(Depth First Search,简称DFS) 与广度优先遍历(Breath First Search,简称BFS)是图论中两种非常重要的算法,生产上广泛用于拓扑排序,寻路(走迷宫),搜索引擎,爬虫等。 一、深度优先遍历 深度优先…...

【Linux】Centos安装mvn命令(maven)
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录一、下载maven包方法一:官…...
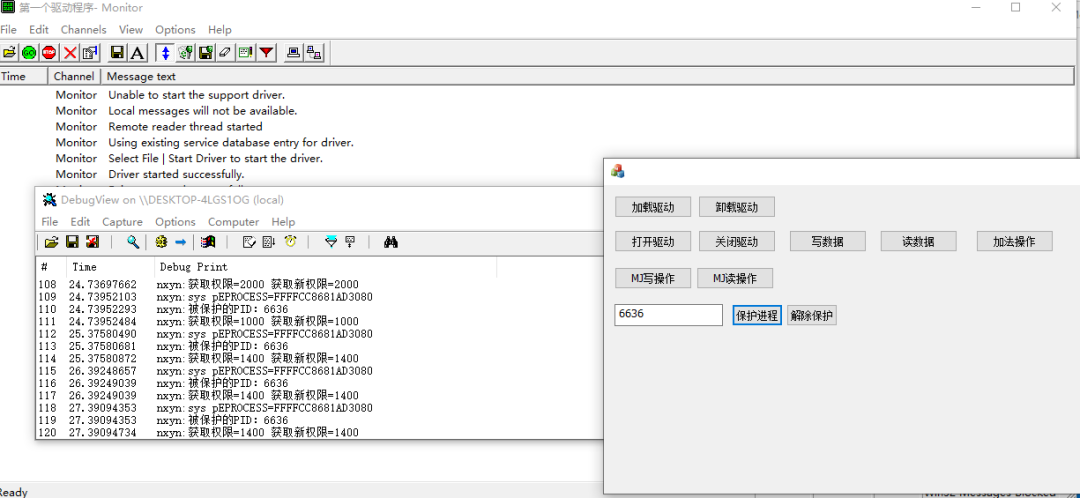
驱动保护 -- 通过PID保护指定进程
一、设计界面 1、添加一个编辑框输入要保护的进程PID,并添加两个按钮,一个保护进程,一个解除保护 2、右击编辑框,添加变量 二、驱动层代码实现 1、声明一个受保护的进程PID数组 static UINT32 受保护的进程PID[256] { 0 }; 2…...

spring常用注解(全)
一、前言 Spring的一个核心功能是IOC,就是将Bean初始化加载到容器中,Bean是如何加载到容器的,可以使用Spring注解方式或者Spring XML配置方式。 Spring注解方式减少了配置文件内容,更加便于管理,并且使用注解可以大大…...

Axios请求(对于ajax的二次封装)——Axios请求的响应结构、默认配置
Axios请求(对于ajax的二次封装)——Axios请求的响应结构、默认配置知识回调(不懂就看这儿!)场景复现核心干货axios请求的响应结构响应格式详解实际请求中的响应格式axios请求的默认配置全局axios默认值(了解…...
【软件设计师】计算机系统—CPU习题联系)
(三)【软件设计师】计算机系统—CPU习题联系
文章目录一、2014年上半年第1题二、2014年下半年第3题三、2017年上半年第1题四、2009年下半年第1题五、2010年上半年第5题六、2011年下半年第5题七、2011年下半年第6题八、2012年下半年第1题九、2019年上半年第1题十、2010年上半年第1题十一、2011年上半年第1题十二、2016年下半…...
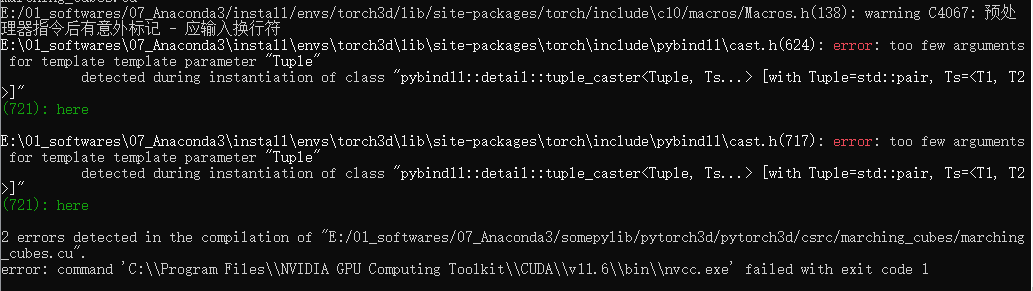
win下配置pytorch3d
一、配置好的环境:py 3.9 pytorch 1.8.0 cuda 11.1_cudnn 8_0 pytorch3d 0.6.0 CUB 1.11.0 你可能觉得pytorch3d 0.6.0版本有点低,但是折腾不如先配上用了,以后有需要再说。 (后话:py 3.9 pytorch 1.12.1 cuda …...

JS字符串对象
、 JS字符串对象 1.1 内置对象简介 在 JavaScript 中,对象是非常重要的知识点。对象可以分为两种:一种是“自定义对象”外一种是“内置对象”。自定义对象,指的是需要我们自己定义的对象,和“自定义函数”是一些道理;内置对象,…...
)
Linux系统对文件及目录的权限管理(chmod、chown)
1、身份介绍 在linux系统中,对文件或目录来说访问者的身份有三种: ①、属主用户,拥有者(owner)文件的创建者 ②、属组用户,和文件的owner同组的用户(group); ③、其他用…...

半透明反向代理 (基于策略路由)
定义 半透明反向代理一般是指 代理本身对于客户端透明,对于服务端可见。 从客户端视角看,客户端访问的还是服务端,客户端不知道代理的存在。 从服务端视角看,服务端只能看到代理,看不到真实的客户端。 示意图 客户端…...

课前测5-超级密码
目录 课前测5-超级密码 程序设计 程序分析 课前测5-超级密码 【问题描述】 上次设计的“高级密码”被你们破解了,一丁小朋友很不服气! 现在,他又设计了一套更加复杂的密码,称之为“超级密码”。 说实话,这套所谓的“超级密码”其实也并不难: 对于一个给定的字符…...

QML控件--Menu
文章目录一、控件基本信息二、控件使用三、属性成员四、成员函数一、控件基本信息 二、控件使用 import QtQuick 2.10 import QtQuick.Window 2.10 import QtQuick.Controls 2.3ApplicationWindow{visible: true;width: 1280;height: 720;Button {id: fileButtontext: "Fi…...

002:Mapbox GL更改大气、空间及星星状态
第002个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中更改大气、空间及星星状态 。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共71行)相关API参考:专栏目标示例效果 配置方式 1)查看基础设置:…...

2022年第十三届蓝桥杯题解(全)C/C++
A题就是一个简单的进制转化,代码实现如下: #include <bits/stdc.h>using namespace std;const int N 1e5 10;int main() {int x 2022;int a 1;int res 0;while(x) {res (x % 10) * a;a a * 9;x / 10;}cout << res;return 0; } B题有…...

【cmake学习】find_package 详解
find_package 主要用于查找指定的 package,主要支持两种搜索方法: Config mode:查找 xxx-config.cmake或 xxxConfig.cmake的文件,如OpenCV库的OpenCVConfig.cmakeModule mode:查找Findxxx.cmake文件,如Ope…...
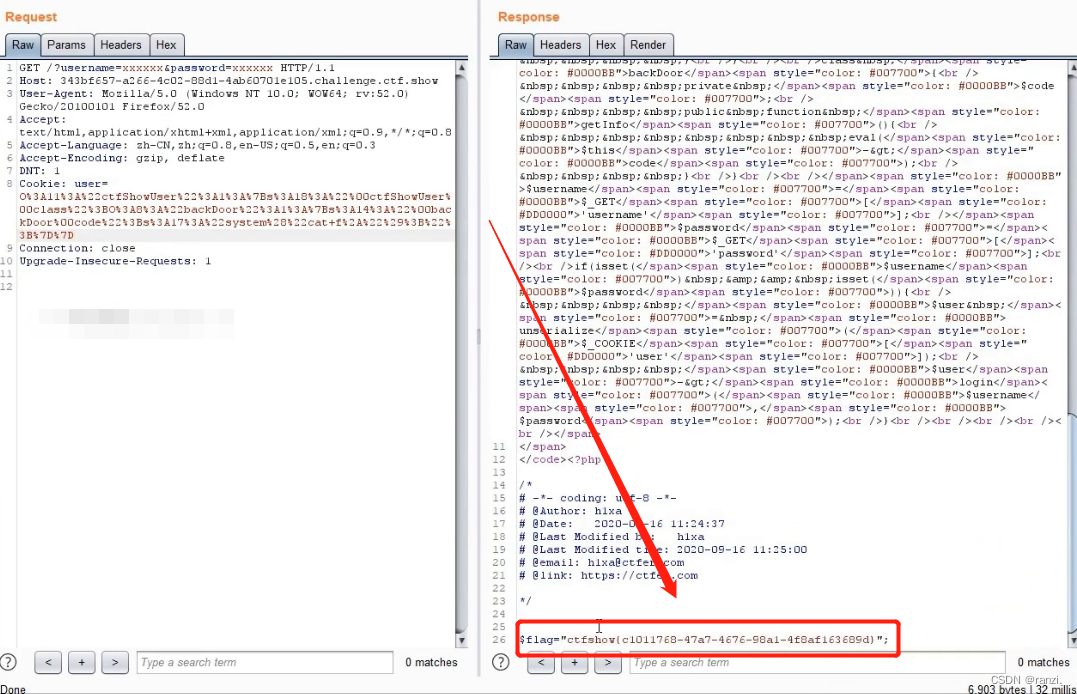
WEB攻防-通用漏洞PHP反序列化POP链构造魔术方法原生类
目录 一、序列化和反序列化 二、为什么会出现反序列化漏洞 三、序列化和反序列化演示 <演示一> <演示二> <演示二> 四、漏洞出现演示 <演示一> <演示二> 四、ctfshow靶场真题实操 <真题一> <真题二> <真题三> &l…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK里的图像处理库进行图像转换(C++)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK进行图像转换(C)Baumer工业相机Baumer工业相机的SDK里图像格式转换的技术背景Baumer工业相机通过BGAPI SDK进行图像转换调用BGAPI SDK的图像转换库ImageProcessor调用BGAPI SDK建立图像调用BGAPI SDK转换图像…...
, 获得店铺的所有商品,获取推荐商品列表, 获取购买到的商品订单列表))
JD开放平台接口(获得JD商品详情, 按关键字搜索商品,按图搜索京东商品(拍立淘), 获得店铺的所有商品,获取推荐商品列表, 获取购买到的商品订单列表)
参数说明 通用参数说明 url说明 https://api-gw.onebound.cn/平台/API类型/ 平台:淘宝,京东等, API类型:[item_search,item_get,item_search_shop等]version:API版本key:调用key,测试key:test_api_keysecret:调用secret,测试secret:(不用填写…...
上海亚商投顾:沪指震荡反弹 游戏、传媒概念股再度大涨
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪大小指数今日走势分化,沪指向上震荡反弹,创业板指一度跌近1%,黄白二线大幅背离。…...

C/C++ 玩转StoneValley库:从入门到精通
C/C 玩转StoneValley库:从入门到精通引言(Introduction)StoneValley库简介(Overview of StoneValley Library)为什么要学习StoneValley库(Why Learn StoneValley Library in C)StoneValley库安装…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
