数据结构——线段树
线段树的结构
线段树是一棵二叉树,其结点是一条“线段”——[a,b],它的左儿子和右儿子分别是这条线段的左半段和右半段,即[a, (a+b)/2 ]和[(a+b)/2 ,b]。线段树的叶子结点是长度为1的单位线段[a,a+1]。下图就是一棵根为[1,10]的线段树:
易证一棵以[a,b]为根的线段树结点数是2*(b-a)-1。由于线段树是一棵平衡树,因此一棵以[a,b]为根结点的线段树的深度为log2(2*(b-a))。
线段树中的结点一般采取如下数据结构:
其中a,b分别表示线段的左端点和右端点,Left,Right表示左儿子和右儿子的编号。因此我们可以用一个一维数组来表示一棵线段树:
Tree:array[1..Maxn] of TreeNode;
a,b,Left,Right这4个域是描述一棵线段树所必须的4个量。根据实际需要,我们可以增加其它的域,例如增加Cover域来计算该线段被覆盖的次数,bj域用来表示结点的修改标记(后面将会提到)等等。
线段树的建立
我们可以用一个简单的过程建立一棵线段树。

线段树中的线段插入和删除
增加一个Cover的域来计算一条线段被覆盖的次数,即数据结构变为:

因此在MakeTree的时候应顺便把Cover置0。
线段的插入
插入一条线段[c,d]

线段的删除
删除一条线段[c,d]

线段树的简单应用
掌握了线段树的建立,插入和删除这3条操作,就能用线段树解决一些最基本的统计问题了。例如给出一系列线段[a,b] (0< a < b < 10000)覆盖在数轴上,然后求该数轴上共有多少个单位长度[k,k+1]被覆盖了。我们便可以在读入一系列线段[a,b]的时候,同时调用过程Insert(1)。等所有线段都插入完后,就可以进行统计了:

像这样的基本静态统计问题,线段树是可以很方便快捷地解决的。但是我们会留意到,如果处理一些动态统计问题,比如说一些需要用到删除和修改的统计,困难就出现了。
『例1』
在数轴上进行一系列操作。每次操作有两种类型,一种是在线段[a,b]上涂上颜色,另一种将[a,b]上的颜色擦去。问经过一系列的操作后,有多少条单位线段[k,k+1]被涂上了颜色。
这时我们就面临了一个问题——线段的删除。但线段树中线段的删除只能是把已经放入的线段删掉,例如我们没有放置[3,6]这条线段,删除[3,6]就是无法做到的了。而这道题目则不同,例如在[1,15]上涂了颜色,我们可以把[4,9]上的颜色擦去,但线段树中只是插入了[1,15]这条线段,要删除[4,9]这条线段显然是做不到的。因此,我们有必要对线段树进行改进。
线段树的改进
【关键词:状态下沉,标志向下扩散】
用回刚刚那个例子。给[1,15]涂上色后,再把[4,9]的颜色擦去。很明显[1,15]这条线段已经不复存在,只剩下[1,4]和[9,15],所以我们必须对线段树进行修改,才能使它符合改变了的现实。我们不难想到把[1,15]这条线段删去,再插入线段[1,4]和[9,15]。但事实上并非如此简单。如下图:
若先前我们已经插入了线段[8,11],[1,8]。按上面的做法,只把[1,15]删去,然后插入[1,4],[9,15]的话,[1,8],[8,11]这两条线段并没有删去,但明显与实际不符了。于是[1,8],[8,11]也要修改。这时疑问就来了。若以线段[1,15]为根的整棵线段树中的所有结点之前都已经插入过,即我们曾经这样涂过颜色:[1,2],[2,3],……,[14,15],[1,3],[3,5],……,[13,15],[1,5],…………,[1,15]。然后把[1,15]上的颜色擦去。那么整个线段树中的所有结点的状态就都与实际不符了,全都需要修改。修改的复杂度就是线段树的结点数,即2*(15-1)=28。如果不是[1,15]这样的小线段,而是[1,30000]这样的线段,一个擦除动作就需要O(59998)的复杂度去修改,显然效率十分低(比直接模拟的O(30000)还差)。
为了解决这个问题,我们给线段树的每一个结点增加一个标记域(以下用bj来表示标记域)。增加一个标记域有什么用呢?如下图:
以[1,5]为根的整棵线段树的全部结点都已涂色。现把[1,5]上的颜色擦去。则整棵线段树的结点的状态都与实际不符了。可是我们并不一定要对所有结点都进行修改,因为有些结点以后可能根本不会有被用到的时候。例如我们做完擦去[1,5]的操作之后,只是想询问[3,5]是否有涂上颜色。那么我们对[1,2],[2,3],[1,3],[3,4],[4,5]等线段的修改就变成无用功了。为了避免无用功的出现,我们引入标记域bj。具体操作如下:
1、擦去线段[a,b]之后,给它的左儿子和右儿子都做上标记,令它们的bj=-1。
2、每次访问一条线段,首先检查它是否被标记,若其bj=-1,则进行如下操作:
①将该线段的状态改为未被覆盖,并把该线段设为未被标记,bj=0。
②把该线段的左右儿子都设为被标记,bj=-1。
对线段[1,5]进行了这样的操作后就不需要对整棵线段树都进行修改了。原理很简单。以线段[3,4]为例。若以后有必要访问[3,4],则必然先访问到它的父亲[3,5],而[3,5]的bj=-1,因此进行①、②的操作后,[3,5]的状态变为未被覆盖,并且把他的标记传递给了他的儿子——[3,4]和[4,5]。接着访问[3,4]的时候,它的bj=-1,我们又把[3,4]的状态变为未被覆盖。可见,标记会顺着访问[3,4]的路一直传递到[3,4],使得我们知道要对[3,4]的状态进行修改,避免了错误的产生。同时,当我们需要用到[3,4]的时候才会进行修改,如果根本不需要用它,修不修改都无所谓了,并不会影响程序的正确性。因此这种方法在保持了正确性的同时有避免了无意义的操作,提高了程序的效率。
进行标记更新的代码如下:

每次访问线段[a,b]之前,首先检查它是否被标记,如果是则调用过程Clear进行状态修改。这样做只是在访问的时候顺便进行修改,复杂度是O(1),程序效率依然很高。
于是,引入标记域后,本题中插入和删除的过程大致如下:
插入过程 Insert
1、若该线段被标记,则调用Clear过程
2、若线段状态为被涂色,则退出过程(线段已被涂色,无需再插入它或它的子线段)
3、若涂色的区域覆盖了该线段,则该线段的状态变为被涂色,并退出过程
4、若涂色的区域与该线段的左半截的交集非空,则调用左儿子的插入过程
5、若涂色的区域与该线段的右半截的交集非空,则调用右儿子的插入过程
删除过程 Delete

1、若该线段被标记,则退出过程(该线段已被赋予被擦除的“义务”,无需再次赋予)
2、若擦除的区域覆盖了该线段,则该线段的状态变为未被涂色,并将其左右儿子都做上标记,退出过程
3、若该线段的状态为被涂色,则
① 该线段状态变为未被涂色
② 将其左右儿子做上标记
③ 插入线段[a,c]和[d,b]
4、若该线段的状态为未被涂色,则
①若擦除区域与该线段的左半截的交集非空,则调用左儿子的擦除过程
②若擦除区域与该线段的右半截的交集非空,则调用右儿子的擦除过程
归纳一下标记域的思想及如何使用。如果我们对整条线段[a,b]进行操作的话,我们就可以只是给[a,b]的左右儿子做上标记,而无需对以[a,b]为根的整棵子树中的所有结点进行修改。原理就是对下面的所有结点[c,d],都有[c,d] [a,b],因此[a,b]状态的改变也就代表了[c,d]状态的改变。
本着这个思想,标记域的使用形式并不是固定的,而是多样的,具体形式如何要视题目而定,但只要理解了它的思想,总能想到如何确定作标记的方式,维持线段树的高效。
相关文章:

数据结构——线段树
线段树的结构 线段树是一棵二叉树,其结点是一条“线段”——[a,b],它的左儿子和右儿子分别是这条线段的左半段和右半段,即[a, (ab)/2 ]和[(ab)/2 ,b]。线段树的叶子结点是长度为1的单位线段[a,a1]。下图就是一棵根为[1,10]的线段树࿱…...

【C++进阶】实现C++线程池
文章目录1. thread_pool.h2. main.cpp1. thread_pool.h #pragma once #include <iostream> #include <vector> #include <queue> #include <thread> #include <mutex> #include <condition_variable> #include <future> #include &…...

Redis常用五种数据类型
一、Redis String字符串 1.简介 String类型在redis中最常见的一种类型 string类型是二制安全的,可以存放字符串、数值、json、图像数据 value存储最大数据量是512M 2. 常用命令 set < key>< value>:添加键值对 nx:当数据库中…...
)
C++ Primer第五版_第十一章习题答案(1~10)
文章目录练习11.1练习11.2练习11.3练习11.4练习11.5练习11.6练习11.7练习11.8练习11.9练习11.10练习11.1 描述map 和 vector 的不同。 map 是关联容器, vector 是顺序容器。 练习11.2 分别给出最适合使用 list、vector、deque、map以及set的例子。 list:…...

GEE:使用LandTrendr进行森林变化检测详解
作者:_养乐多_ 本文介绍了一段用于地表变化监测的代码,该代码主要使用谷歌地球引擎(GEE)中的 Landsat 时间序列数据,采用了 Kennedy 等人(2010) 发布的 LandTrendr 算法,对植被指数进行分割,通过计算不同时间段内植被指数的变化来检测植被变化。 目录 一、加入矢量边界 …...
docker项目实施
鲲鹏916架构openEuler-arm64成功安装docker并跑通tomcat容器_闭关苦炼内功的技术博客_51CTO博客鲲鹏916架构openEuler-arm64成功安装docker并跑通tomcat容器,本文是基于之前这篇文章鲲鹏920架构arm64版本centos7安装docker下面开始先来看下系统版本卸载旧版本旧版本…...
springboot实现邮箱验证码功能
引言 邮箱验证码是一个常见的功能,常用于邮箱绑定、修改密码等操作上,这里我演示一下如何使用springboot实现验证码的发送功能; 这里用qq邮箱进行演示,其他都差不多; 准备工作 首先要在设置->账户中开启邮箱POP…...
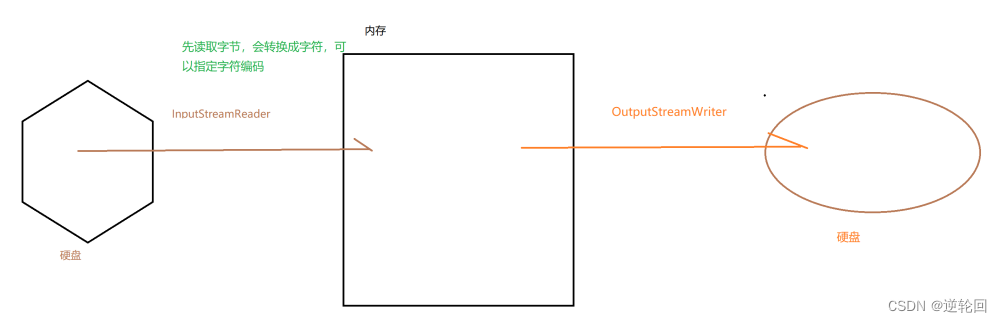
Java 进阶(5) Java IO流
⼀、File类 概念:代表物理盘符中的⼀个⽂件或者⽂件夹。 常见方法: 方法名 描述 createNewFile() 创建⼀个新文件。 mkdir() 创建⼀个新⽬录。 delete() 删除⽂件或空⽬录。 exists() 判断File对象所对象所代表的对象是否存在。 getAbsolute…...
“终于我从字节离职了...“一个年薪40W的测试工程师的自白...
”我递上了我的辞职信,不是因为公司给的不多,也不是因为公司待我不好,但是我觉得,我每天看中我憔悴的面容,每天晚上拖着疲惫的身体躺在床上,我都不知道人生的意义,是赚钱吗?是为了更…...

设计模式之策略模式(C++)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 一、策略模式是什么? 策略模式是一种行为型的软件设计模式,针对某个行为,在不同的应用场景下&…...

从工厂普工到Python女程序员,聊聊这一路我是如何逆袭的?
我来聊聊我是如何从一名工厂普工,到国外程序员的过程,这里面充满了坎坷。过去我的工作是在工厂的流水线上,我负责检测电池的正负极。现如今我每天从早上6:20起床,6点四五十分出发到地铁站,7:40到公司。我会给自己准备一…...

全国青少年信息素养大赛2023年python·选做题模拟二卷
目录 打印真题文章进行做题: 全国青少年电子信息智能创新大赛 python选做题模拟二卷 一、单选题 1. numbers = [1, 11, 111, 9], 运行numbers.sort() 后,运行numbers.reverse() numbers会变成?( )...

分布式事务Seata原理
Seata 是一款开源的分布式事务解决方案,致力于提供高性能与简单易用的分布式事务服务,为用户提供了 AT、TCC、SAGA 和 XA 几种不同的事务模式。Seata AT模式是基于XA事务演进而来,需要数据库支持。AT 模式的特点就是对业务无入侵式࿰…...
用ChatGPT怎么赚钱?普通人用这5个方法也能赚到生活费
ChatGPT在互联网火得一塌糊涂,因为它可以帮很多人解决问题。比如:帮编辑人员写文章,还可以替代程序员写代码,帮策划人员写文案策划等等。ChatGPT这么厉害,能否用它来赚钱呢?今天和大家分享用ChatGPT赚钱的5…...
( “树” 之 DFS) 110. 平衡二叉树 ——【Leetcode每日一题】
110. 平衡二叉树 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 示例 1: 输入:root [3,9,20,null,null,15,7] …...
nvm软件使用-同一个环境下控制多个不同node版本
1.使用场景 nvm是一个用于管理Node.js版本的工具,它可以让你在同一台机器上安装和切换不同的Node.js版本。使用nvm的好处有以下几点: 1.1.nvm可以让你轻松地测试你的代码在不同的Node.js版本下的兼容性和性能,避免因为版本差异导致的问题。…...

连续两个南航的研究生面试出了从来没出现过的问题,本科和研究生都是计算机专业的,竟然说static是不可更改的。
最近面试人数有点多,面试有点频繁,因此发现了一些学生普遍会发生的错误,可以说是很离谱。 因为做了十多年的面试官,无论是大中小厂的面试,还是社招、校招。 从来没有遇到过这样的情况,而且发生在两个南航…...

How to install nacos/nacos-server:v2.1.2-slim with docker
今天给大家介绍一下如何基于Docker的nacos/nacos-server:v2.1.2-slim镜像安装nacos 1、Data Source 我们需要从nacos的github官网下载nacos 2.12发布包 nacos-server-2.1.2.tar.gznacos-server-2.1.2.zip 这里以nacos-server-2.1.2.tar.gz为例来介绍,解压后我们…...

Rust社区引发舆论危机,问题到底出在哪儿?
围绕开源的法律问题,讨论焦点往往集中在开源许可证、软件著作权等方面,商标的讨论却极少引人关注。事实上,关于开源软件以及开源软件的衍生产品的商标使用情况往往处于某种灰色地带。 最近,Rust基金会正在就更新的商标政策征求反馈…...

C++算法恢复训练之归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法,它将待排序数组分成两个子数组,然后对这两个子数组分别进行排序,最后将两个已排序的子数组合并成一个有序数组。归并排序是一种稳定的排序算法,具体体现…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
