C++算法恢复训练之归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法,它将待排序数组分成两个子数组,然后对这两个子数组分别进行排序,最后将两个已排序的子数组合并成一个有序数组。归并排序是一种稳定的排序算法,具体体现在其时间复杂度上。
下面是使用 C++ 实现的归并排序算法:
#include <algorithm>
#include <iostream>
#include <random>
#include <vector>using namespace std;void mergeSortImplementation(vector<int>& array, int left, int right)
{if (left == right){return;}const int mid = left + ((right - left) >> 1);mergeSortImplementation(array, left, mid);mergeSortImplementation(array, mid + 1, right);vector<int> temp(right - left + 1);int p1 = left;int p2 = mid + 1;for (unsigned int i = 0; i < temp.size(); ++i){if (p1 == mid + 1){temp[i] = array[p2++];continue;}if (p2 == right + 1){temp[i] = array[p1++];continue;}if (array[p1] < array[p2]){temp[i] = array[p1++];}else{temp[i] = array[p2++];}}for (unsigned int i = left; i < right + 1; ++i){array[i] = temp[i - left];}
}void mergeSort(vector<int>& array)
{if (array.size() < 2){return;}mergeSortImplementation(array, 0, array.size() - 1);
}int main(int argc, char* argv[])
{// Create an array to test sort methodvector<int> array = {2, 3, 4, 0, 7};cout << "Before sorting: ";for (int i = 0; i < array.size(); ++i){cout << array[i] << " ";}cout << endl;mergeSort(array);cout << "After sorting: ";for (int i = 0; i < array.size(); ++i){cout << array[i] << " ";}cout << endl;return 0;
}归并排序的实现过程可以分为两个步骤:
- 分割子问题:将待排序数组分成两个子数组,分别对两个子数组进行排序。
- 合并解决方案:将两个已排序的子数组合并成一个有序数组。
具体来说,归并排序的分割子问题的实现可以使用递归算法,每次将待排序数组分成两个子数组,然后对两个子数组分别进行排序;合并解决方案的实现则需要额外的存储空间,将两个已排序的子数组合并成一个有序数组。
归并排序的时间复杂度为 O(nlogn)O(nlogn)O(nlogn),其中 n 是待排序数组的长度。归并排序每次将待排序数组分成两个子数组,分别对两个子数组进行排序,然后再将两个已排序的子数组合并成一个有序数组。这个过程的时间复杂度可以表示为:
T(n)=2T(n/2)+O(n)T(n) = 2T(n/2) + O(n)T(n)=2T(n/2)+O(n)
其中 T(n) 表示对长度为 n 的数组进行归并排序的时间复杂度。通过递归展开可以得到:
T(n)=2T(n/2)+O(n)=2[2T(n/4)+O(n/2)]+O(n)=4T(n/4)+2O(n)=4[2T(n/8)+O(n/4)]+2O(n)=8T(n/8)+3O(n)=...=nT(1)+lognO(n)T(n) = 2T(n/2) + O(n)\\ = 2[2T(n/4) + O(n/2)] + O(n)\\ = 4T(n/4) + 2O(n)\\ = 4[2T(n/8) + O(n/4)] + 2O(n)\\ = 8T(n/8) + 3O(n)\\ = ...\\ = nT(1) + lognO(n)T(n)=2T(n/2)+O(n)=2[2T(n/4)+O(n/2)]+O(n)=4T(n/4)+2O(n)=4[2T(n/8)+O(n/4)]+2O(n)=8T(n/8)+3O(n)=...=nT(1)+lognO(n)
故而其最终算法时间复杂度为O(nlogn)O(nlogn)O(nlogn)。
相关文章:

C++算法恢复训练之归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法,它将待排序数组分成两个子数组,然后对这两个子数组分别进行排序,最后将两个已排序的子数组合并成一个有序数组。归并排序是一种稳定的排序算法,具体体现…...

使用Process Explorer和Clumsy工具定位软件高CPU占用问题
目录 1、问题描述 2、使用Process Explorer初步找到CPU占用高的原因 3、使用Clumsy工具在公司内网环境复现了问题...

为何巴菲特和马斯克站在了一起?
股神巴菲特虽然非常传奇,但是马斯克对其并不感冒。马斯克曾经在一档电视节目中表示,实业才是王道,埋怨金融业抢走太多人才和精英,暗指巴菲特为年轻人做了错误示范。当然,巴菲特的投资非常厉害,但也有失手的…...

企业数字化转型全是坑?这几篇数字化转型成功案例,减少70%损失
这篇给大家整理了200企业数字化转型案例合集,涵盖了制造、建筑、教育、零售、互联网等10行业的大中小型企业数字化转型思路,希望对大家有所帮助。 案例全部整合在这篇文章中,点击即可查看>>数字化干货资料合集! 01 首先&…...

13.Java面向对象----嵌套类
Java面向对象—嵌套类、内部类、匿名类 一、static静态 在《Java编程思想》有这样一段话: “static方法就是没有this的方法。在static方法内部不能调用非静态方法,反过来是可以的。而且可以在没有创建任何对象的前提下,仅仅通过类本身来…...

Redis数据迁移过程,使用jedis客户端发送命令,需要注意string和byte类型的命令,如果使用的转换字符编码不一致,会导致丢数据
1.了解String与byte之间存在的字符编码映射规则(java为例) string与byte来回转换,需要指定一样字符编码规则 详细原因请参考:关于Java中bytes到String的转换-阿里云开发者社区 简单来说 (1)string和by…...

第六章 IA-32指令类型
IA-32指令类型1、传送指令1.1、常用传送指令1.1.1、通用数据传送指令1.2、传送指令执行过程2、定点算术运算指令2.1、常用定点运算指令2.2、加法运算的底层实现举例2.3、加法指令和乘法指令举例3、按位运算指令3.1、逻辑运算和移位运算3.2、按位运算指令举例4、控制转移指令4.1…...
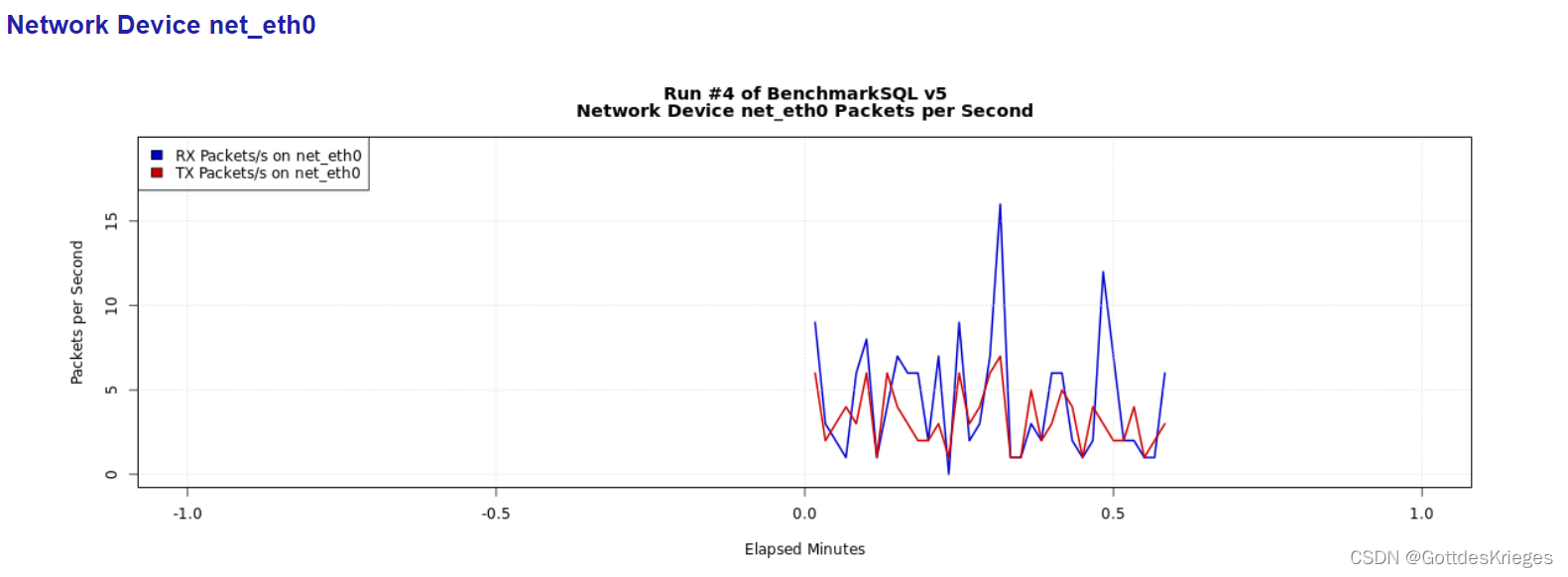
基于BenchmarkSQL的Oracle数据库tpcc性能测试
基于BenchmarkSQL的Oracle数据库tpcc性能测试安装BenchmarkSQL及其依赖安装软件依赖编译BenchmarkSQLBenchmarkSQL props文件配置数据库用户配置BenchmarkSQL压测装载测试数据TPC-C压测(固定事务数量)TPC-C压测(固定时长)生成测试…...

Dapr和Rainbond集成,实现云原生BaaS和模块化微服务开发
背景 Dapr 是一个开源的分布式应用运行时,帮助开发者构建松耦合的分布式应用程序,具有良好的可扩展性和可维护性。Rainbond 是一款企业级的云原生应用管理平台,提供了丰富的功能和工具,方便开发者管理和部署应用。Rainbond 和 Da…...

全国青少年信息素养大赛2023年python·选做题模拟五卷
目录 下载打印文档做题: 全国青少年电子信息智能创新大赛 python选做题模拟五卷 一、单选题 1. 对于数列3,8,11,15,17,19,25,30,44,采用“二分查找”法查找8,需要查找多少次?( ) A、5...

itop-3568开发板驱动学习笔记(18)tasklet 机制
《【北京迅为】itop-3568开发板驱动开发指南.pdf》 学习笔记 文章目录tasklet 简介tasklet 结构体tasklet 初始化使能 tasklet失能 tasklettasklet 调度函数tasklet 取消调度函数tasklet 实验tasklet 简介 Tasklets 机制是linux中断处理机制中的软中断延迟机制。在linux中存在着…...
python·模拟二卷)
全国青少年电子信息智能创新大赛(复赛)python·模拟二卷
目录 编程题一 答案解析: 打印题目下载做题: 全国青少年电子信息智能创新大赛(复赛)python模拟二卷 编程题一 第一题:描述 输入两个整数,比较它们的大小。 输入 一行,包含两个整数x和y,中间用单个空格隔开。 0<= x<2^32,-2^31 <= y<2^31。 输出...

对标ChatGPT的开源中文方案
目录 前言 一、Meta发布大语言模型LLaMA 二、斯坦福基于 Meta 的 LLaMA 7B 模型微调出Alpaca 三、基于TencentPretrain训练中文LLaMA大规模语言模型 四、基于斯坦福Alpaca训练中文对话大模型BELLE 五、 清华开源项目ChatGLM中文对话模型 六、基于LLaMA的开源中文语言模型…...

9.Java面向对象----封装
Java面向对象—封装 面向对象简称 OO(Object Oriented),20 世纪 80 年代以后,有了面向对象分析(OOA)、 面向对象设计(OOD)、面向对象程序设计(OOP)等新的系统…...

【react 全家桶】组合组件
本人大二学生一枚,热爱前端,欢迎来交流学习哦,一起来学习吧。 <专栏推荐> 🔥:js专栏 🔥:vue专栏 🔥:react专栏 文章目录09 【组合组件】1.包含关系2.特例关系问题…...
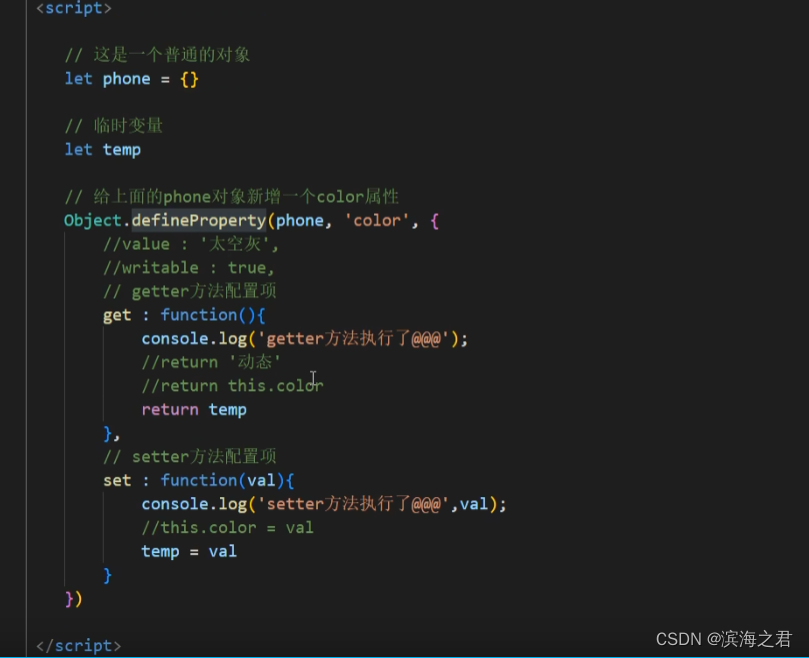
VUE_学习笔记
一、 xx 二、模板语法 1.模板语法之差值语法 :{{ }} 主要研究:{{ 这里可以写什么}} 在data中声明的变量、函数等都可以。常量只要是合法的javascript表达式,都可以。模板表达式都被放在沙盒中,只能访问全局变量的一个白名单&a…...
【分布式事务AT模式 SpringCloud集成Seata框架】分布式事务框架Seata详细讲解
前言 上篇文章我们讲述了如何启动seata的本地服务,并且注册到nacos使用,这篇文章将在SpringCloud中整合Seata框架 上篇文章传送门:https://blog.csdn.net/Syals/article/details/130102851?spm1001.2014.3001.5501 本篇主要内容ÿ…...

系统集成项目管理工程师软考第三章习题(每天更新)
第一章指路:系统集成项目管理工程师软考第一章习题(已完结)_程序猿幼苗的博客-CSDN博客 第二章指路:系统集成项目管理工程师软考第二章习题(已完结)_程序猿幼苗的博客-CSDN博客 第3章信息系统集成专业技术…...
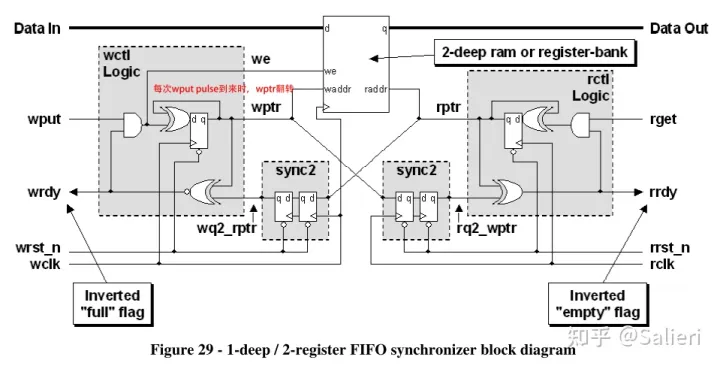
FIFO的工作原理及其设计
1.简介 FIFO( First Input First Output)简单说就是指先进先出。FIFO存储器是一个先入先出的双口缓冲器,即第一个进入其内的数据第一个被移出,其中一个口是存储器的输入口,另一个口是存储器的输出口。 对于单片FIFO来说,主要有两种…...

「UG/NX」Block UI 通过浏览器选择文件File Selection with Browse
目录 控件说明界面效果公有属性对话框标题 DialogLabel(仅创建)控件灰显 Enable分组 Group(仅创建)控件显隐 Show控件标题 Label国籍文本 AllowInternationalTextInput(仅创建)显示密文 IsPassword(仅创建)本地化 Localize(仅创建)保存值 RetainValue属性界面代码实现…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
