剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数
难度:middle\color{orange}{middle}middle
题目描述
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
复制示例输入
示例 2:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]复制示例输入
限制:
1<=n<=111 <= n <= 111<=n<=11
算法
(动态规划)
设输入 n 个骰子的解(即概率列表)为 f(n) ,其中「点数和」 x 的概率为 f(n,x) 。
假设已知 n−1 个骰子的解 f(n−1) ,此时添加一枚骰子,求 n 个骰子的点数和为 x 的概率 f(n,x) 。
当添加骰子的点数为 1 时,前 n−1 个骰子的点数和应为 x−1 ,方可组成点数和 x ;同理,当此骰子为 2 时,前 n−1 个骰子应为 x−2 ;以此类推,直至此骰子点数为 6 。将这 6 种情况的概率相加,即可得到概率 f(n,x) 。递推公式如下所示:
f(n,x)=∑i=16f(n−1,x−i)∗1/6f(n, x) = \sum_{i=1}^6f(n - 1, x - i) * 1 / 6f(n,x)=∑i=16f(n−1,x−i)∗1/6
复杂度分析
-
时间复杂度:O(n2)O(n^2)O(n2)
-
空间复杂度 : O(n)O(n)O(n)
C++ 代码
class Solution {
public:vector<double> dicesProbability(int n) {vector<double> res(n * 5 + 1);vector<vector<double>> f(n + 1, vector<double>(n * 6 + 1, 0));for (int i = 1; i <= 6; i ++)f[1][i] = 1.0 / 6;for (int i = 2; i <= n; i ++)for (int j = i; j <= i * 6; j ++)for (int k = 1; k <= 6; k ++){if (j - k >= i - 1)f[i][j] += f[i - 1][j - k]/6;}for (int i = 0; i <= n * 5; i ++)res[i] = f[n][n + i];return res;}
};
相关文章:

剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数 难度:middle\color{orange}{middle}middle 题目描述 把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。 你需要用一个浮点数数组返回答案,其中第 i 个…...

阿里巴巴-淘宝搜索排序算法学习
模型效能:模型结构优化 模型效能:减枝 FLOPS:每秒浮点运算的次数 模型效能:量化 基于统计阈值限定,基于学习阈值限定。 平台效能:一站式DL训练平台 平台效能:搜索模型的系统流程 协同关系…...

〖Python网络爬虫实战⑮〗- pyquery的使用
订阅:新手可以订阅我的其他专栏。免费阶段订阅量1000python项目实战 Python编程基础教程系列(零基础小白搬砖逆袭) 说明:本专栏持续更新中,目前专栏免费订阅,在转为付费专栏前订阅本专栏的,可以免费订阅付费…...
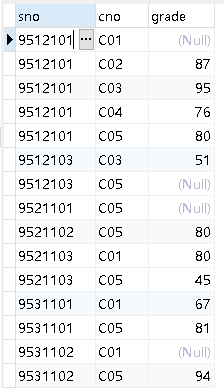
SQL综合查询下
SQL综合查询下 目录SQL综合查询下18、查询所有人都选修了的课程号与课程名题目代码题解19、SQL查询:查询没有参加选课的学生。题目代码20、SQL查询:统计各门课程选修人数,要求输出课程代号,课程名,有成绩人数ÿ…...

全连接层FC
lenet结构: 输入层(Input Layer):接收手写数字的图像数据,通常是28x28的灰度图像。 卷积层1(Convolutional Layer 1):对输入图像进行卷积操作,提取低级别的特征,使用 6 个大小为 5x5 的卷积核进行卷积,得到 6 个输出特征图,激活函数为 Sigmoid。 平均池化层1(Aver…...

图的遍历及连通性
文章目录 图的遍历及连通性程序设计程序分析图的遍历及连通性 【问题描述】 根据输入的图的邻接矩阵A,判断此图的连通分量的个数。 【输入形式】 第一行为图的结点个数n,之后的n行为邻接矩阵的内容,每行n个数表示。其中A[i][j]=1表示两个结点邻接,而A[i][j]=0表示两个结点无…...
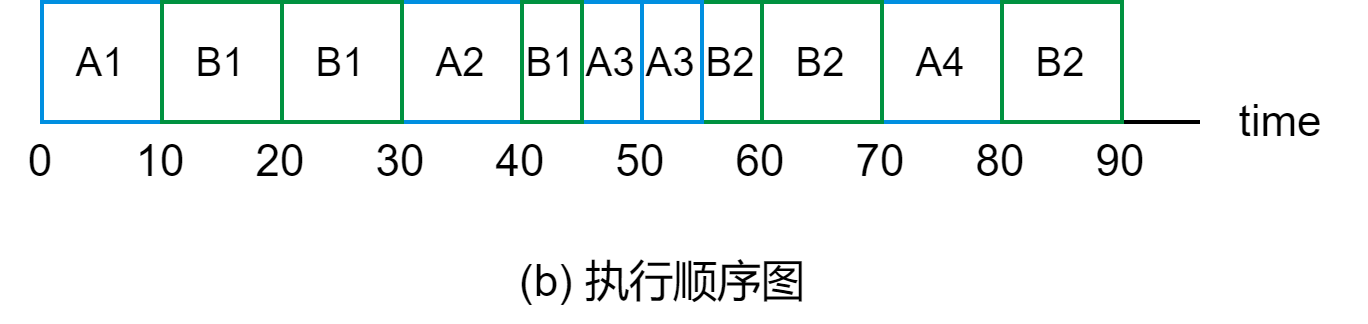
DJ3-4 实时调度
目录 3.4.1 实现实时调度的基本条件 1. 提供必要的信息 2. 系统的处理能力强 3. 采用抢占式调度机制 4. 具有快速切换机制 3.4.2 实时调度算法的分类 1. 非抢占式调度算法 2. 抢占式调度算法 3.4.3 常用的几种实时调度算法 1. 最早截止时间优先 EDF(Ea…...
)
Oracle之PL/SQL游标练习题(三)
游标练习题目1、定义游标:列出每个员工的姓名部门名称并编程显示第10个到第20个记录2、定义游标:从雇员表中显示工资大于3000的记录,只要姓名、部门编号和工资,编程显示其中的奇数记录3、用游标显示所有部门编号与名称,…...
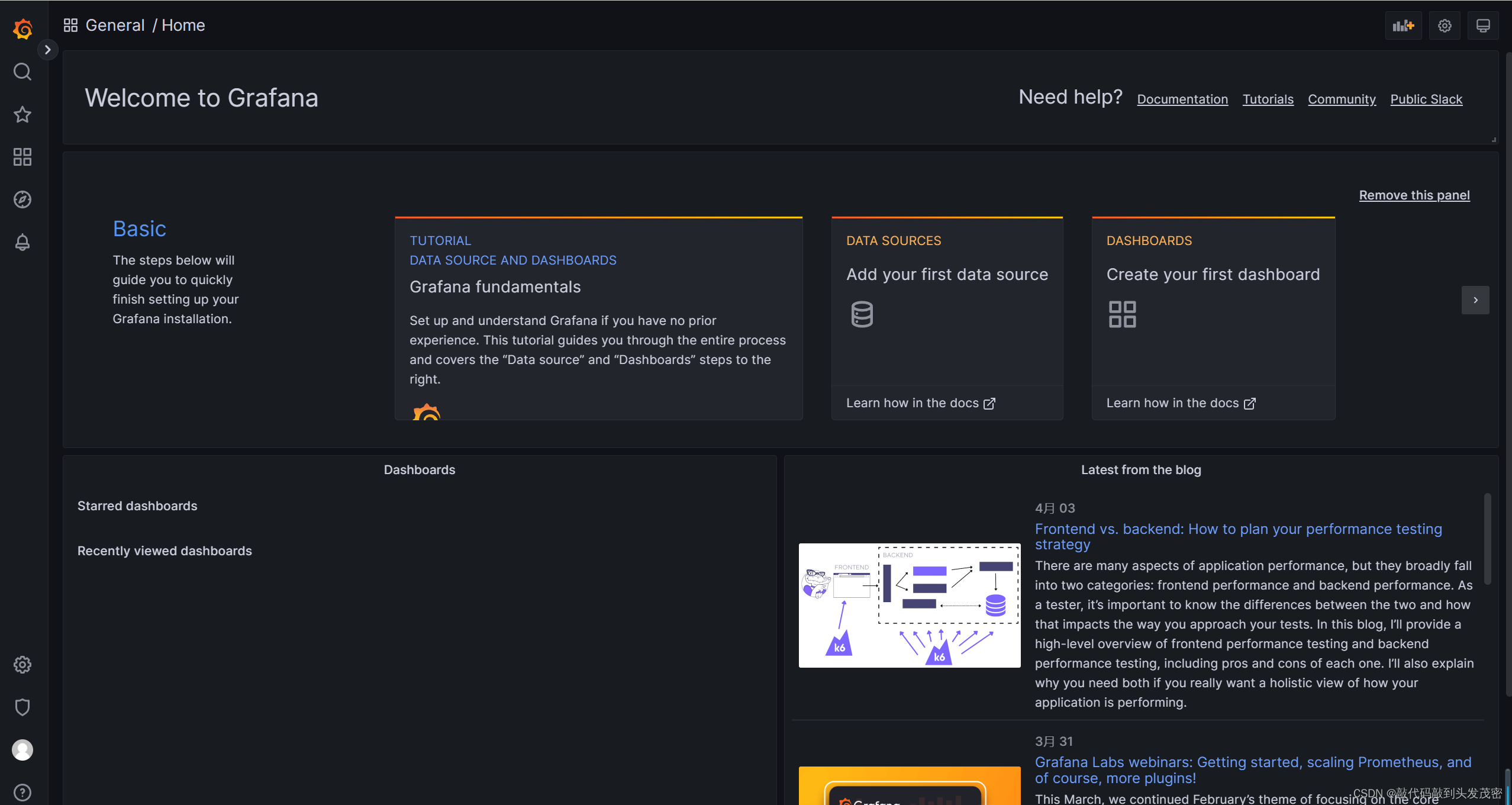
docker运行服务端性能监控系统Prometheus和数据分析系统Grafana
文章目录一、Prometheus的安装和运行1、使用docker拉取镜像2、创建prometheus.yml文件3、启动容器4、查看启动是否成功5、记录安装过程中出现的错误二、Grafana的安装和运行1、使用docker拉取镜像2、创建grafana3、运行grafana4、查看grafana运行日志5、登录grafana一、Prometh…...

【Linux】【应用层】多线程编程
一、线程创建 Linux 中的 pthread_create() 函数用来创建线程,它声明在<pthread.h>头文件中,语法格式如下: int pthread_create(pthread_t *thread,const pthread_attr_t *attr,void *(*start_routine) (void *),void *arg);各个参数…...

GameFramework 框架详解之 如何接入热更框架HybridCLR
一.前言 HybridCLR是一个特性完整、零成本、高性能、低内存的近乎完美的c#热更新方案 GameFramework是一个非常出色完整的基于Unity引擎的游戏框架,里面包含了非常多的模块,封装非常完整。 以前市面上的热更大多数都是Lua为主,后来出了一个ILRuntime的C#热更框架,虽然性能…...
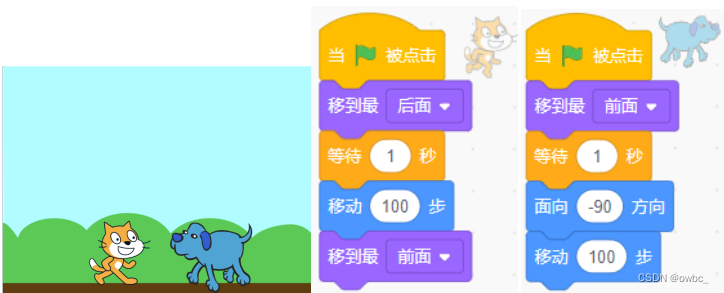
全国青少年软件编程(Scratch)等级考试二级考试真题2023年3月——持续更新.....
一、单选题(共25题,共50分) 1. 小猫的程序如图所示,积木块的颜色与球的颜色一致。点击绿旗执行程序后,下列说法正确的是?( ) A.小猫一直在左右移动,嘴里一直说着“抓到了”。 B.小猫会碰到球,然后停止。 C.小猫一直在左右移动,嘴里一直说着“别跑” D.小猫会碰到球,…...
HTML2.1列表标签
列表标签种类 无序列表 有序列表 自定义列表 使用场景:在列表中按照行展示关联性内容。 特点:按照行的形式,整齐显示内容。 一、无序列表 标签名说明ul无序列表整体,用于包裹li标签li表示无序列表的每一项,用于包…...
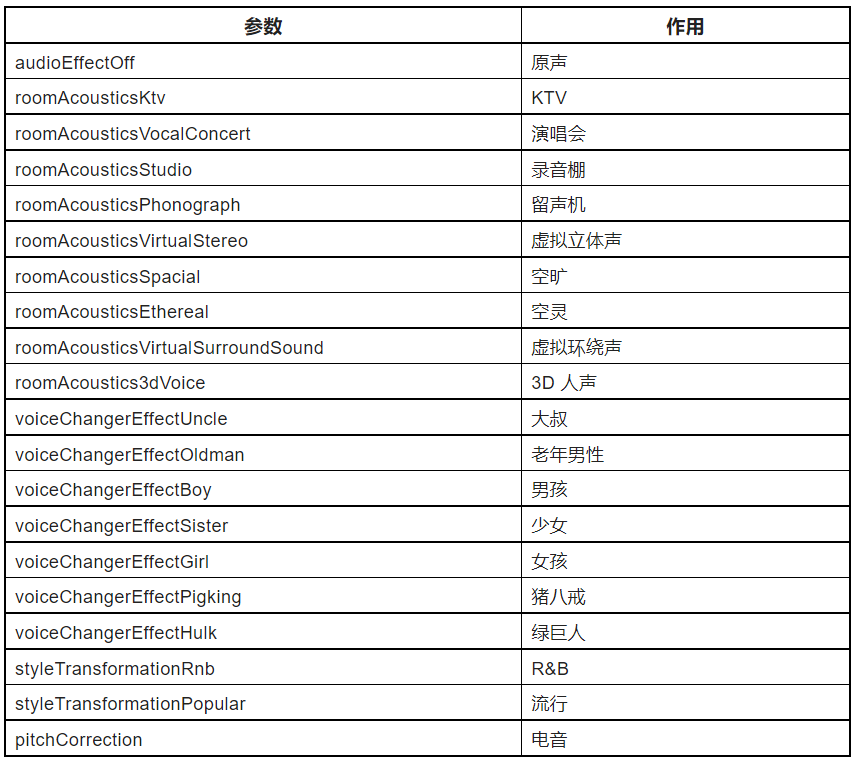
在 Flutter 多人视频通话中实现虚拟背景、美颜与空间音效
前言 在之前的「基于声网 Flutter SDK 实现多人视频通话」里,我们通过 Flutter 声网 SDK 完美实现了跨平台和多人视频通话的效果,那么本篇我们将在之前例子的基础上进阶介绍一些常用的特效功能,包括虚拟背景、色彩增强、空间音频、基础变声…...

Ambari-web 架构
Ambari-web 使用的前端 Embar.js MVC 框架实现,Embar.js 是一个 TodoMVC 框架,涵盖了单页面应用(single page application)几乎所有的行为 Nodejs 是一个基于 Chrome JavaScript 运行时建立的一个平台,用来方便的搭建…...

对接百思买Best Buy EDI 的注意事项
在此前的文章:《Best Buy Drop Ship(Commerce hub) EDI业务测试常见报错及解决》中,我们介绍了在业务测试过程中遇到的常见报错及解决方案,以下在此基础上进行补充。 数据未能成功发送给Best Buy可能遇到的情况 Best Buy EDI项目传输业务报…...

2023年郑州重点建设项目名单公布,中创“算力数据中心”项目入选!
4月7日,郑州市人民政府网站公布2023年郑州市重点建设项目名单,名单共列项目680个,总投资1.08万亿元,年度计划投资2691亿元。 在创新驱动能力提升项目名单里,中创算力与人民网人民数据(国家大数据灾备中心&a…...

Pytorch 容器 - 1. Module类介绍
目录 1. 基于Module构建自己的网络 2. Module的初始化变量 3. Modules中需要子类 forward() 4. Modules中其他内置函数 1. 基于Module构建自己的网络 torch.nn.Module是所有神经网络模块的基类,如何定义自已的网络: 由于 Module 是神经网络模块的基…...

百度墨卡托坐标转化笔记
一、墨卡托坐标转化 调研了python和java多种实现方式的转换,发现有的不符合需求,原因还没找到。 我是用百度地图返回的poi边界(返回的是墨卡托坐标) 转换的原理没有深入研究,直接拿来用的,测试可行&…...

每日学术速递4.12
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.HC 随着新的“生成代理”论文的发布,LLM刚刚达到了一个重要的里程碑——通过使用 LLM,生成代理能够在受《模拟人生》启发的交互式沙箱中模拟类人行为。代理架构扩展…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
