准备2023（2024）蓝桥杯
前缀和
一维前缀和
s[i]=s[i-1]+a[i]
二维前缀和（子矩阵的和）
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
差分
一维数组
//b是差分数组b[i]+=c;b[j+1]-=c;
例题
#include<iostream>
using namespace std;
int n,m;
int b[100002],a[100002];
void insert(int i,int j,int c)
{b[i]+=c;b[j+1]-=c;
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];insert(i,i,a[i]);}for(int i=1;i<=m;i++){int l,r,c;cin>>l>>r>>c;insert(l,r,c);}for(int i=1;i<=n;i++){a[i]=a[i-1]+b[i];cout<<a[i]<<' ';}
}
二维差分（差分矩阵）
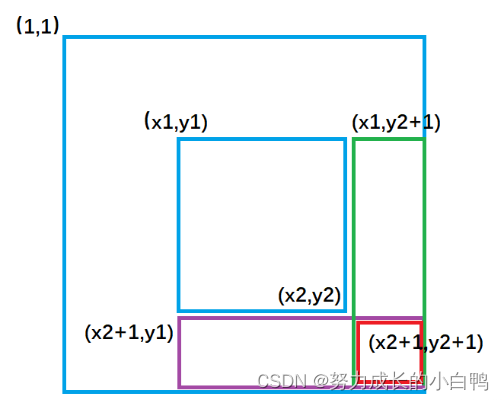
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
例题：
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){insert(i, j, i, j, a[i][j]); //构建差分数组}}while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]+b[i][j]; //二维前缀和}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", a[i][j]);}printf("\n");}return 0;
}字符串的操作STL
#include<string>
string s;
s.size();
s.length();
tolower(a);//将大写字母a，转换为小写字母，返回值是小写字母；a=tolower(a);
字符串
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
using namespace std;
string s[10];//可以读入二维的字符串
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>s[i];}for(int i=1;i<=n;i++){cout<<s[i]<<endl;}
}
模拟
模拟题可难也可简单，重点是 读懂题意，抽象出来模型（我这说的好像是废话 ）
例题（简单）
#include <iostream>
#include<string>
using namespace std;
int n,m;
string a[102];
int d[8][2]={{-1,1},{1,-1},{0,1},{0,-1},{1,1},{-1,-1},{1,0},{-1,0}};
int main()
{cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<n;i++){for(int j=0;j<m;j++){int ans=0;if(a[i][j]=='*'){cout<<a[i][j];continue;}for(int k=0;k<8;k++){if((i+d[k][0])>=0&&(i+d[k][0]<n)&&(j+d[k][1]>=0)&&j+d[k][1]<m&&a[i+d[k][0]][j+d[k][1]]=='*'){ans++;}}cout<<ans;}cout<<endl;}return 0;
}闰年的判断
bool is_leap(int n)
{if((n%4==0&&n%100!=0)||(n%400==0)){return true;}return false;
}
高精度
高精度加法
例题
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B,C;
string a,b;
void add()
{int t=0;for(int i=0;i<A.size()||i<B.size();i++){if(i<A.size()){t+=A[i];}if(i<B.size()){t+=B[i];}C.push_back(t%10);t=t/10;}if(t){C.push_back(t);}
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}add();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}高精度乘法
高精度乘低精度
例题
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B,C;
string a;
int b;
void mul()
{int t=0;for(int i=0;i<A.size();i++){t+=A[i]*b;C.push_back(t%10);t=t/10;}if(t){C.push_back(t);}while(C.size()>1&&C.back()==0){C.pop_back();//把前导零删除}
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}mul();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}高精度乘高精度
例题
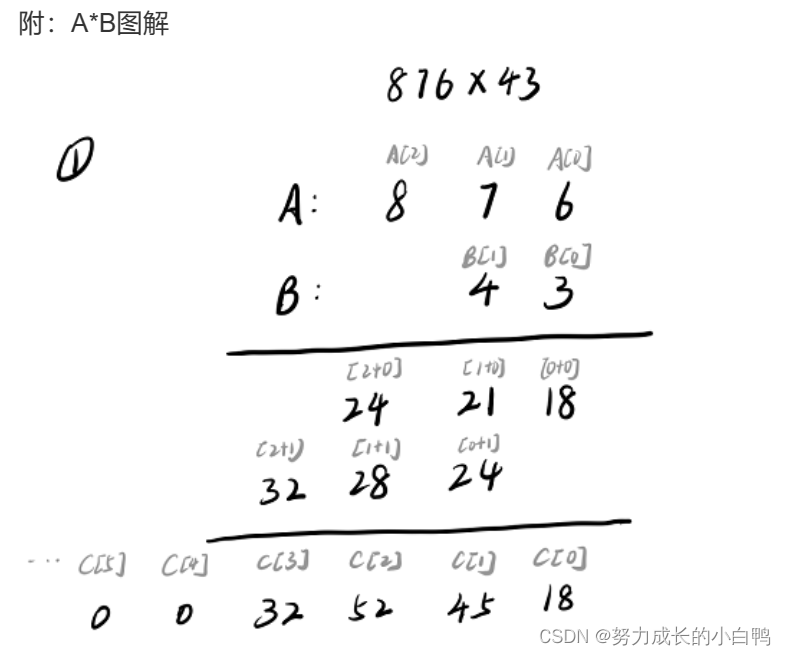
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B;
string a,b;
vector<int> mul()
{vector<int>C(A.size()+B.size()+7,0);int t=0;for(int i=0;i<B.size();i++){for(int j=0;j<A.size();j++){C[i+j]+=B[i]*A[j];}}for(int i=0;i<C.size();i++){t+=C[i];C[i]=t%10;t/=10;}if(t){C.push_back(t);}while(C.size()>1&&C.back()==0){C.pop_back();}return C;
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}auto C=mul();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}数学知识
卡特兰数
C0 = 1,
C1 = 1, C2 = 2, C3 = 5, C4 = 14, C5 = 42,
C6 = 132, C7 = 429, C8 = 1430, C9 = 4862, C10 = 16796,
C11 = 58786, C12 = 208012, C13 = 742900, C14 = 2674440, C15 = 9694845,
C16 = 35357670, C17 = 129644790, C18 = 477638700, C19 = 1767263190, C20 = 6564120420, ...递推公式
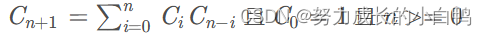
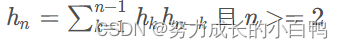
#include <iostream>
#include<algorithm>
using namespace std;
//卡特兰数，用的是第二个公式
const int n=10;
int c[n];
int main()
{c[1]=1,c[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){c[i]+=c[j]*c[i-j];}}for(int i=1;i<=n;i++){printf("c[%d]=%d\n",i,c[i]);}return 0;
}
相关题目练习可以参考这位大佬的总结
组合数学
例题
#include<iostream>
using namespace std;
int n;
const int mod=1e9+7;
const int N = 2004;
int c[2004][2004];int a,b;
void init()
{for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(!j){c[i][j]=1;}else{c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;}}}
}
int main()
{cin>>n;init();while(n--){scanf("%d%d",&a,&b);cout<<c[a][b]<<endl;}
}
例题
#include <iostream>//只有70分，不过是绿题啊，第一次做绿题，所以这种数学知识，如果没见过就超级难，一旦学过也就还好。using namespace std;
const int N=2e3+3;
long long t,k;
unsigned long long c[N][N];
void cal()
{c[0][0]=0;for(int i=0;i<=2000;i++){for(int j=0;j<=i;j++){if(j==0){c[i][j]=1;}else{c[i][j]=c[i-1][j]+c[i-1][j-1];}}}
}
int main()
{long long ans=0;cal();cin>>t>>k;int a,b;while(t--){scanf("%d%d",&a,&b);for(int i=0;i<=a;i++){for(int j=0;j<=min(i,b);j++){// cout<<c[i][j]<<' ';if(c[i][j]%k==0){ans++;}}}cout<<ans<<endl;ans=0;}return 0;
}素数筛（欧拉筛）
bool st[N];//st[i]为1，说明被筛掉了，也就是说，不是素数
int cnt=0;
for(int i=2;i<=n;i++)
{if(!st[i]){primes[cnt++]=i;for(int j=i+i;j<=n;j+=i){st[j]=1;}}
}例题
#include <iostream>using namespace std;
const int N = 1e8+2;
bool st[N];
int primes[N];
int cnt;
int n,m;
void is_primes()
{for(int i=2;i<=n;i++){if(!st[i]){cnt++;primes[cnt]=i;for(int j=i+i;j<=n;j+=i){st[j]=1;}}}
}//TLE，只有四十分，埃氏筛效率还是低了些。1e8会TLE，例如一个数 24，它会被 2, 3, 4 三个数标记，这就重复了两次，更大的数同理。
int main()
{cin>>n>>m;int q;is_primes();while(m--){scanf("%d",&q);printf("%d\n",primes[q]);}return 0;
}线性筛
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
质因子分解
定理：一个合数可以由多个比他小的质数相乘而得，而这些质数就是他的质因数。
//要计算的是从1到n之间的所有合数的质因数
for(int i=1;i<=n;i++)
{int x=i;if(!st[x])//没有被筛掉，也就是是合数{continue;}else{for(int j=2;j<=x;j++){while(x%j==0){p[cnt++]=j;//p数组中存的是质因数x=x/j;}}}
}
用map实现
例题
#include<iostream>
#include<map>
using namespace std;
void fen(int n)
{map<int,int> m;for(int i=2;i<=n/i;i++){if(n%i==0){int c=0;while(n%i==0){c++;n=n/i;}m[i]+=c;}}if(n>=2)//加上大于根号n的素因子{m[n]++;}map<int,int>::iterator iter;for(iter=m.begin();iter!=m.end();iter++){printf("%d %d\n",iter->first,iter->second);}cout<<endl;
}
int main()
{int n,a;cin>>n;while(n--){scanf("%d",&a);fen(a);}return 0;
}
约数个数定理
套用上面map实现的代码
void fen(int n)
{map<int,int> m;for(int i=2;i<=n/i;i++){if(n%i==0){int c=0;while(n%i==0){c++;n=n/i;}m[i]+=c;}}if(n>=2)//加上大于根号n的素因子{m[n]++;}map<int,int>::iterator iter;for(iter=m.begin();iter!=m.end();iter++){//printf("%d %d\n",iter->first,iter->second);res*=(iter->second+1);//这里}cout<<endl;
}
分离整数
while(n)
{a.push_back(n%10);//依次存储的是个位 十位等n=n/10;
}
例题
得到各个位数
//前三位
int n=1234567;
int x=n/10000;
//取后两位
int y=n%100;
进制转换
#include<iomanip>
setbase(n)
//hex十六进制，oct八进制，dec十进制
最大公约数
int gcd(int a,int b)
{return b==0?a:gcd(b,a%b);
}
例题
这个例题中，主要是字符串的操作，最大公约数只是其中的一个应用，但是如果不会最大公约数和最小公倍数的话，也会很麻烦
#include<cstdio>
#include<iostream>
using namespace std;
int a,b,c,d;
int gcd(int x,int y)
{if(y==0)return x;return gcd(y,x%y);
}
int main()
{scanf("%d/%d",&a,&b);//这一步就很巧妙while(scanf("%d/%d",&c,&d)!=EOF)//EOF是先按Enter键，然后是Ctrl+z{int m=(b*d)/gcd(b,d);//最小公倍数*最大公约数=a*ba=a*(m/b)+c*(m/d);b=m;int x=gcd(a,b);a=a/x;b=b/x;//cout<<a<<'/'<<b<<endl;}if(b<0){a=-a;b=-b;}if(b==1)printf("%d\n",a);elseprintf("%d/%d\n",a,b);return 0;
}快速幂运算
例题
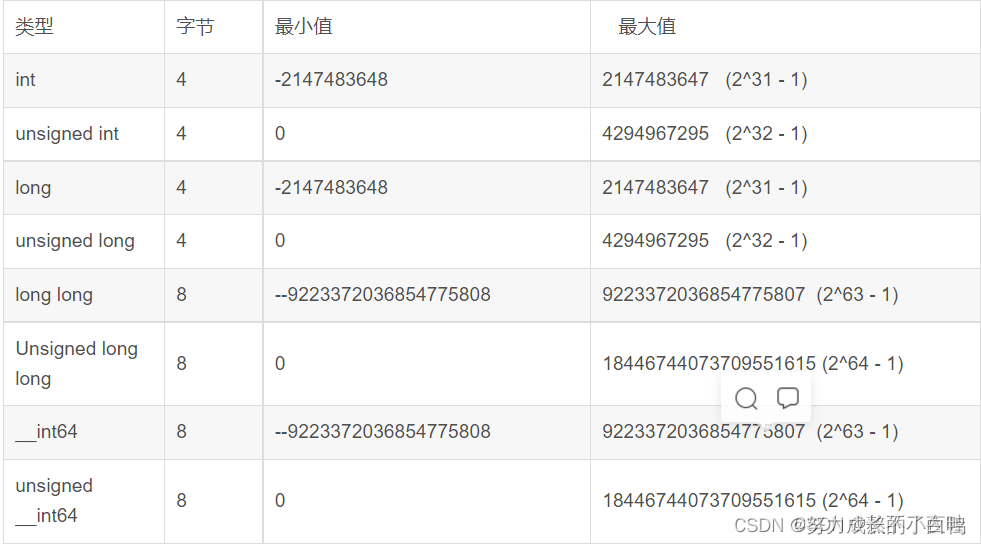
ps:十年OI一场空，不开long long见祖宗
附上数据范围
#include <iostream>using namespace std;
long long a,b,p;
int n;
typedef long long ll;
ll qmi(ll a,ll b,ll q)
{ll res=1;while(b){if(b&1){res=((res%p)*(a%p))%p;}b>>=1;a=(a*a)%p;}return res;
}
int main()
{cin>>n;while(n--){cin>>a>>b>>p;cout<<qmi(a,b,p)<<endl;}return 0;
}贪心算法
取当前情况最好的，贪心不贪，重点在于排序加模拟。
例题
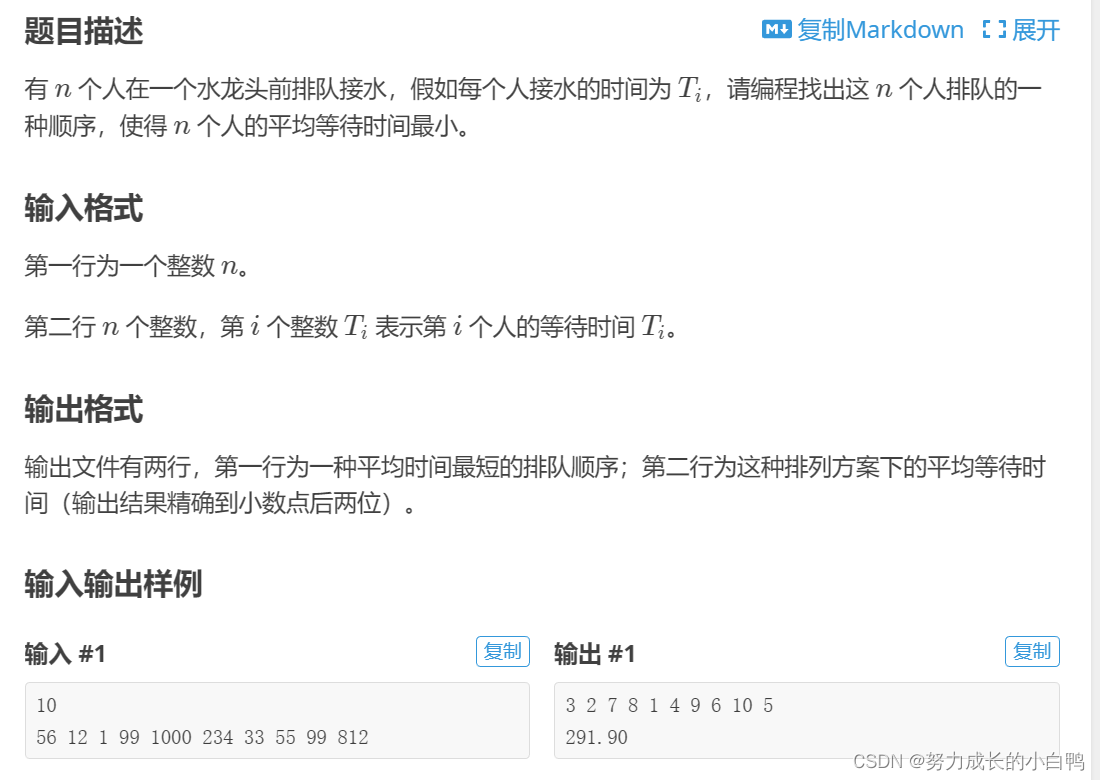
思路：等待时间最小，就是让接水时间最短的人先接。用sort排个序，因为是要输出排队的序号，所以就用pair了
#include <iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n;
int sum[1002];
pair<int,int>a[1002];
bool cmp(pair<int,int>x,pair<int,int>y)
{return x.second < y.second;
}
int main()
{cin>>n;for(int i=1;i<=n;i++){a[i].first=i;cin>>a[i].second;}sort(a+1,a+n+1,cmp);for(int i=1;i<=n;i++){cout<<a[i].first<<' ';}cout<<endl;memset(sum,0,sizeof(sum));for(int i=2;i<=n;i++){sum[i]=sum[i-1]+a[i-1].second;}double ans;for(int i=2;i<=n;i++){ans+=sum[i];}ans=ans*1.0/n;printf("%.2lf",ans);return 0;
}例题
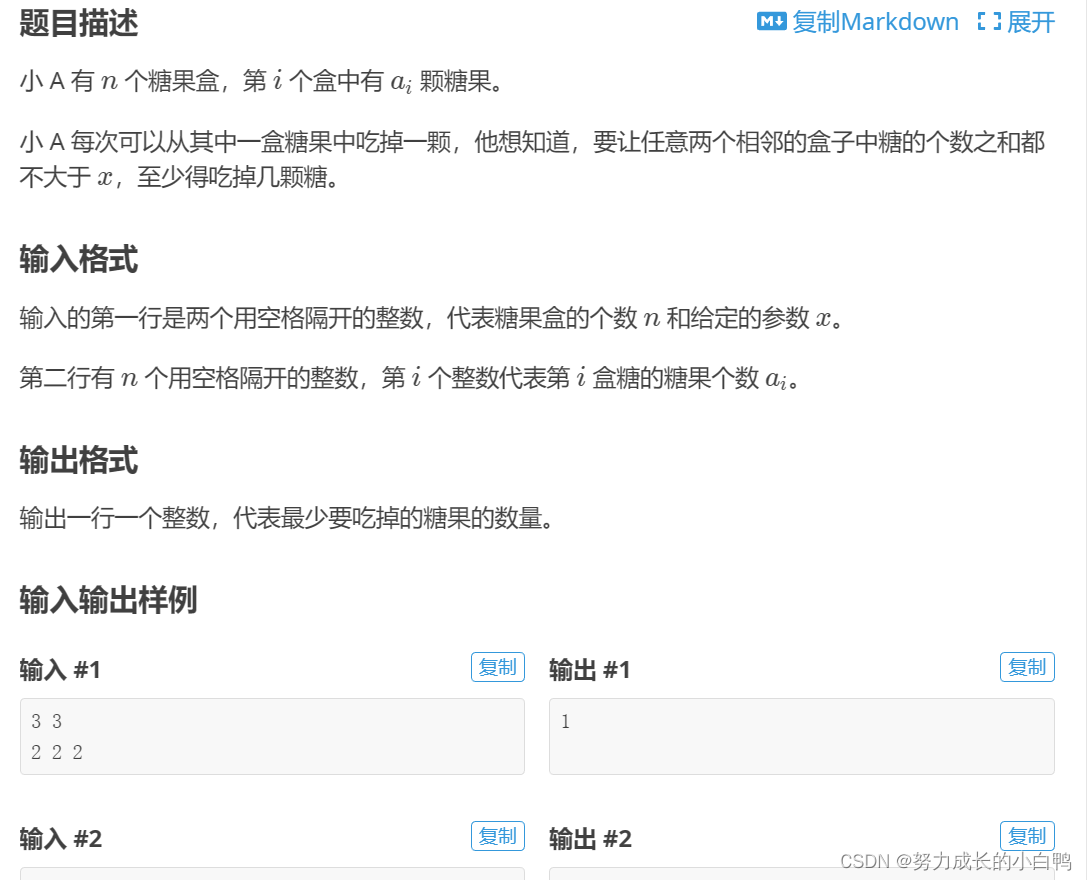
思路：贪心就是取当前情况最好的。在这道题中，正向遍历，如果两者之和大于x,就吃掉a[i]中的，如果a[i]为0了，就吃掉a[i-1]中的糖果。因为后面还有，如果先吃掉a[i-1]中的，对后面没啥影响，所以不是最好的情况。（至于理论证明为啥这样最好，本蒟蒻不会5555）
#include <iostream>
#include<algorithm>
#include<cmath>
using namespace std;
long long n,x;
long long a[100004];
int main()
{cin>>n>>x;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}long long t=0;long long ans=0;long long temp=0;for(int i=2;i<=n;i++){if(a[i-1]+a[i]>x){temp=a[i];t=a[i-1]+a[i]-x;ans+=t;a[i]=a[i]-t;if(a[i]<0){a[i]=0;a[i-1]=a[i-1]-(x-temp);//开始吃a[i-1]中的糖果}}}cout<<ans<<endl;return 0;
}
例题：
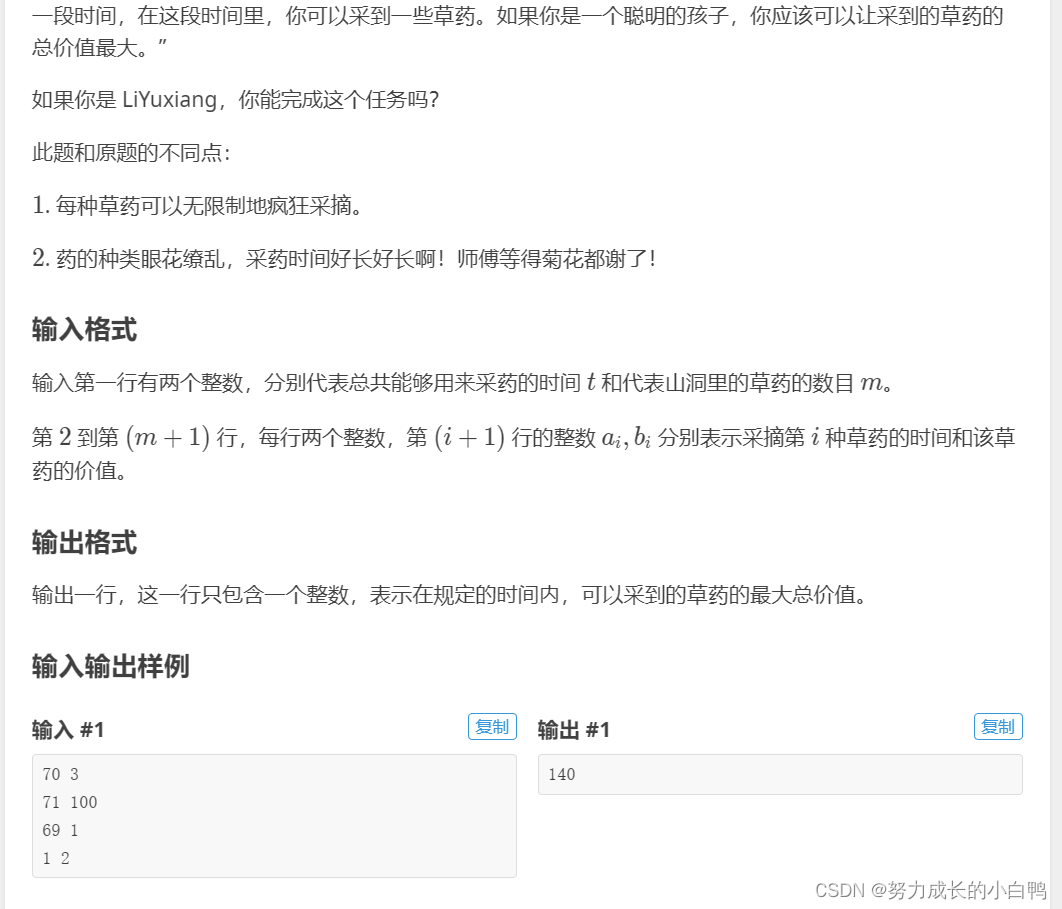
思路：这道题的标签是动态规划，但是数据范围有点大，而且俺也不会完全背包问题，及啥滚动数组，就用贪心做了，but只有90分。哭辽
#include <iostream>
#include<algorithm>
using namespace std;
int t,m;
const int N =1e4+2;
pair<int,int> p[N];
int d[N][N];
bool cmp(pair<int,int>x,pair<int,int>y)
{return (x.second*1.0/x.first) > (y.second*1.0/y.first);
}
int main()
{cin>>t>>m;int a,b;for(int i=0;i<m;i++){cin>>a>>b;p[i].first=a;p[i].second=b;}sort(p,p+m,cmp);long long cost=t;long long val=0;//十年 OI 一场空，不开 long long 见祖宗。for(int i=0;i<m;i++){while(cost>0){val+=p[i].second;cost-=p[i].first;}if(cost<0){cost+=p[i].first;val-=p[i].second;}if(cost==0){break;}}cout<<val;return 0;
}动态规划
格式化输出
//在C++中，cout<<int(2.56);输出就是2，只保留整数部分，如果要四舍五入，就要加上0.5
//可以用printf("%.2lf",2.56);自动进行四舍五入。此外，printf("%02d",6);表示输出占两位，不足两位添加前导0
STL
贴个大佬总结的STL食用指南
//自定义排序方式
bool cmp(int x,int y)
{return x>y;
}//表示按照从大到小的方式进行。这种定义方式，在pair或者结构体中使用范围更广
//例如
bool cmp(pair<int,int>x,pair<int,int>y)
{return x.first > y.first;
}//按照first的值升序排列；
//需要包含在头文件algorithm中
sort(a,a+n,cmp);//a为普通数组
sort(a,a+n,greater<int>());//降序，默认是升序
sort(a.begin(),a.end());//a为vector数组
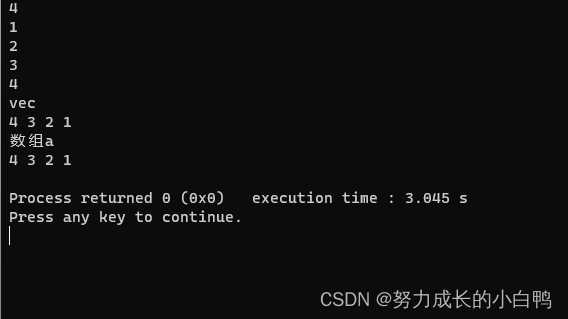
reverse函数
用法示例（vector和数组）
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int main()
{vector<int> vec;int a[10];int n;cin>>n;for(int i=0;i<n;i++){int c;cin>>c;vec.push_back(c);a[i]=c;}reverse(vec.begin(),vec.end());reverse(a,a+n);cout<<"vec"<<endl;for(int i=0;i<n;i++){cout<<vec[i]<<' ';}cout<<endl;cout<<"数组a"<<endl;for(int i=0;i<n;i++){cout<<a[i]<<' ';}cout<<endl;
}
去重（要求序列是有序的，首先用sort排序）
v.erase(unique(v.begin(),v.end()),v.end());
优先队列
priority_queue<Type, Container, Functional>set
map
桶计数是map一个功能之一
#include<bits/stdc++.h>
using namespace std;
map<int,int>book;
int n;
int main()
{cin>>n;for(int i=1;i<=n;i++){int temp;cin>>temp;book[temp]++;}int k;cin>>k;cout<<book[k]<<endl;return 0;
}
二分查找
binary_search（起始地址，结束地址，要查找的数值）
返回值是 是否存在这么一个数，是一个bool值。
binary_search(a,a+n,3);
lower_bound（起始地址，结束地址，要查找的数值），返回值就是返回第一次出现大于等于那个要查找的数的地址；如果不存在则返回a.end()
lower_bound(a,a+n,3)-a;
upper_bound（起始地址，结束地址，要查找的数值）返回的是被查序列中第一个大于查找的数的指针；,如果不存在则返回a.end()
upper_bound(a,a+n,3)-a;
综合应用
查询某个元素出现的次数
upper_bound - lower_bound
upper_bound(a,a+n,3)-lower_bound(a,a+n,3);
例题
#include <iostream>
#include<algorithm>
using namespace std;
int n,c;
const int N = 2e5+5;
int a[N];
int main()
{cin>>n>>c;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}sort(a+1,a+n+1);long long ans=0;//没开long long，只有90分//int posg=upper_bound(a+1,a+n+1,c)-a;这是之前的思路，只有76分for(int i=1;i<=n;i++){//cout<<"a[i"<<a[i]<<endl;ans+=(upper_bound(a+1,a+n+1,a[i]+c))-(lower_bound(a+1,a+1+n,a[i]+c));}cout<<ans<<endl;return 0;
}例题
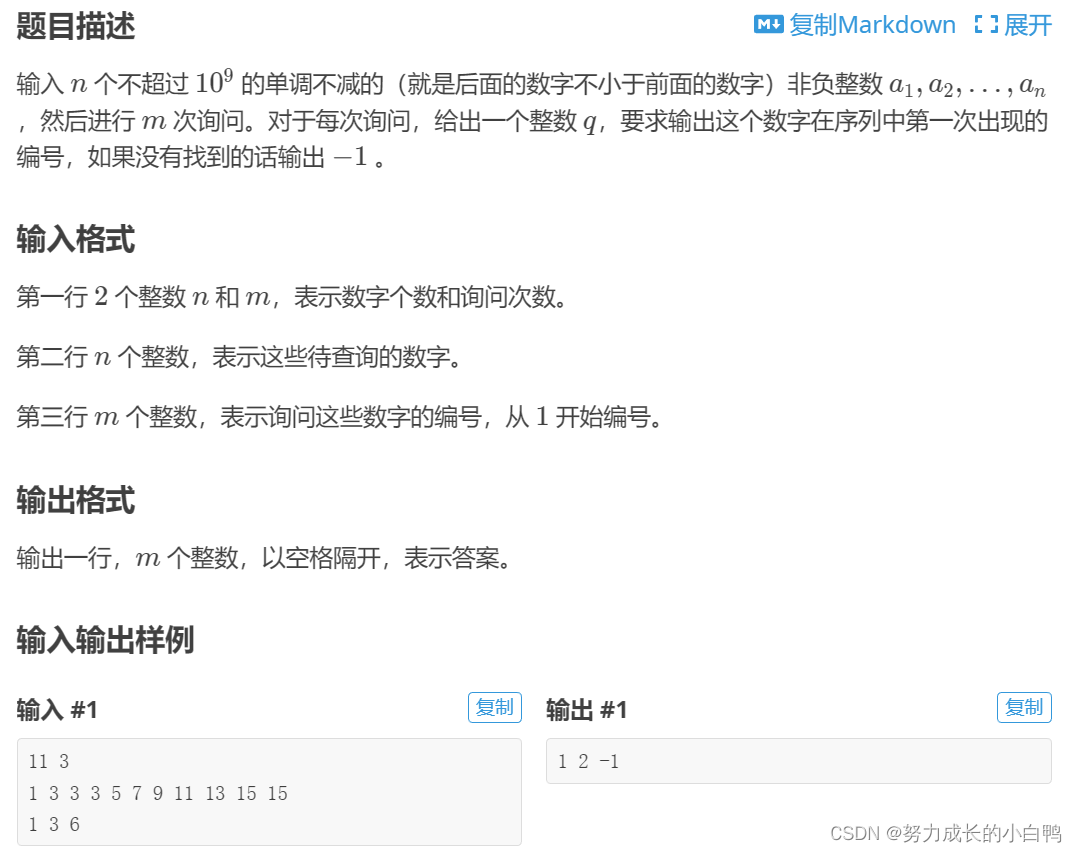
#include <iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 1e6+3;
int a[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}int q;while(m--){cin>>q;if(!binary_search(a+1,a+1+n,q)){cout<<-1<<' ';}else{int x=lower_bound(a+1,a+1+n,q)-a;cout<<x<<' ';}}return 0;
}动态规划
考虑小规模。思考的时候，是由n-1推n,由n-2推n-1;写方程的时候，从1推2，推n
背包问题
0-1背包问题
例题
有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。第 i件物品的体积是 vi，价值是 wi。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i件物品的体积和价值。
输出格式
输出一个整数，表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8
0-1背包（朴素版）
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N=1005;
int v[N],w[N],f[N][N];//f[i][j]表示背包容量为j时前i个物品的最大价值
int main()
{cin>>n>>m;//读入物品的数量和背包容量for(int i=1;i<=n;i++){cin>>v[i]>>w[i];//读入每个物品的重量和价值}//dpfor(int i=1;i<=n;i++){for(int j=0;j<=m;j++){if(j<v[i])f[i][j]=f[i-1][j];//如果背包容量小于物品的重量，那就不装else{f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i])//如果背包容量大于物品的重量，这时候就有两种选择，装或者不装，如果装入的话，j就要减去第i个物品的重量，这两种情况取其中的最大值}}}cout<<f[n][m]<<endl;return 0;
0-1背包（升级版）
解释：由于进行状态转移的过程中只用到了上一层的数据，所以可以进行降维。
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 1e3+5;
int f[N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){ f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;return 0;
}
完全背包问题（朴素版）
完全背包问题和0-1背包问题的区别就是每一种物品的个数是无限的。
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N][N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;v[i]*k<=j;k++){if(j<v[i]){f[i][j]=f[i-1][j];}else{f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}}cout<<f[n][m]<<endl;return 0;
}
优化版
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N][N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;return 0;
}
完全背包（再升级版）
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;return 0;
}
多重背包（朴素版）
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 110;
int f[N][N],v[N],w[N],s[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i]>>s[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k<=s[i]&&k*v[i]<=j;k++){f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);}}}cout<<f[n][m]<<endl;return 0;
}
搜索bfs
使用队列，queue
例题
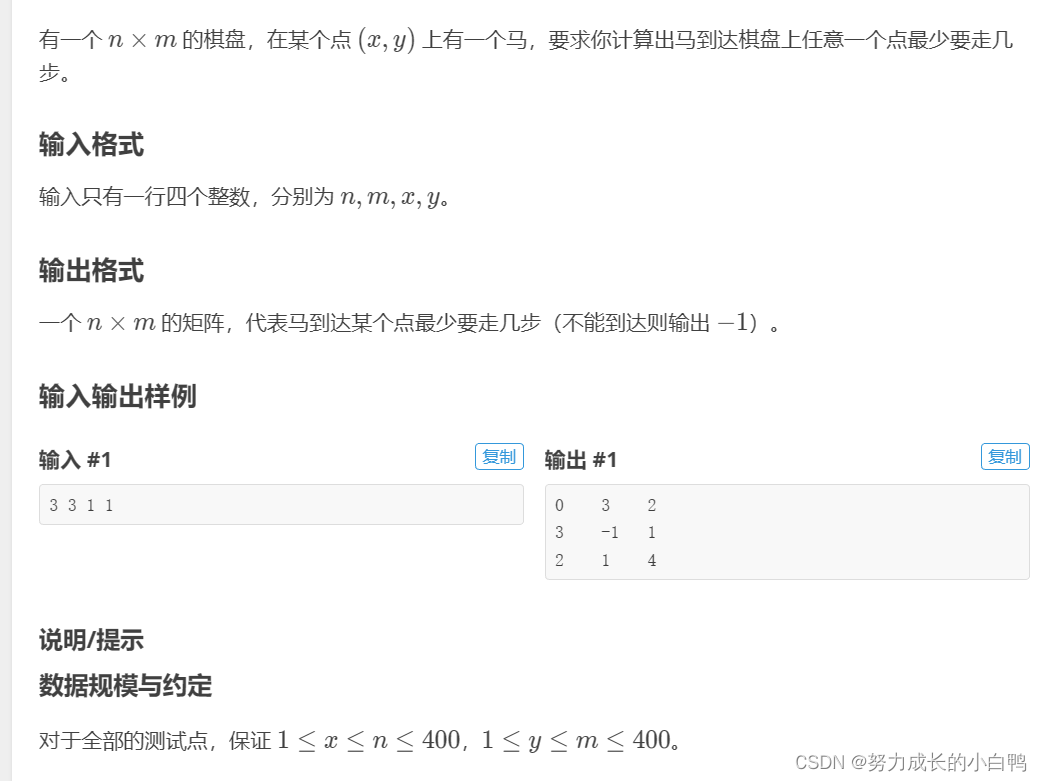
思路：本来想用最短路算法，迪杰斯特拉，看到题目标签是bfs，就用了bfs，我是菜鸡，呜呜。这题用pair正好。
#include <iostream>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
queue<PII>q;
const int N = 405;
int mp[N][N];
int d[8][2]={{1,-2},{1,2},{2,-1},{2,1},{-1,-2},{-1,2},{-2,-1},{-2,1}};
int vis[N][N];
int dis[N][N];
int n,m,x,y;
void bfs(int x,int y)
{PII temp;temp.first=x;temp.second=y;q.push(temp);vis[temp.first][temp.second]=1;while(!q.empty()){temp=q.front();q.pop();//vis[temp.first][temp.second]=0;此处不需要写，否则会死循环for(int i=0;i<8;i++){int tx,ty;tx=temp.first+d[i][0];ty=temp.second+d[i][1];if(tx>=0&&tx<n&&ty>=0&&ty<m&&!vis[tx][ty]){q.push(make_pair(tx,ty));vis[tx][ty]=1;dis[tx][ty]=dis[temp.first][temp.second]+1;}}}
}
int main()
{cin>>n>>m>>x>>y;bfs(x-1,y-1);for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(dis[i][j]==0){if(i==x-1&&j==y-1){cout<<0<<' ';}else{cout<<-1<<' ';}}else{cout<<dis[i][j]<<' ';}}cout<<endl;}return 0;
}
dfs
搞清楚状态转移
全排列问题
//头文件algorithm
int a[4]={1,2,3,4};
do
{for(int i=0;i<4;i++){cout<<a[i]<<' ';}cout<<endl;
}while(next_permutation(a,a+4));
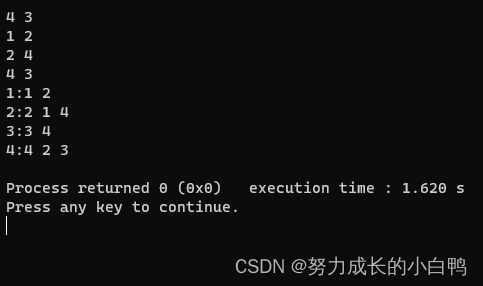
图的基本应用
邻接表（用vector实现）
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+3;
int vis[N];
vector<int>v[N];
queue<int> q;
int main()
{int n,m;cin>>n>>m;int a,b;for(int i=1;i<=n;i++){v[i].push_back(i);}for(int i=0;i<m;i++){cin>>a>>b;v[a].push_back(b);v[b].push_back(a);}for(int i=1;i<=n;i++){int len=v[i].size();int maxx=0;cout<<i<<':';for(int j=0;j<len;j++){cout<<v[i][j]<<' ';}//cout<<maxx<<' ';cout<<endl;}return 0;
}
单源最短路径
迪杰斯特拉算法
例题同下（这个算法不是靠队列实现的）
依然只有60分，因为我用的还是邻接矩阵
#include <iostream>
#include<cstring>
using namespace std;
const int N=1e4;
const int INF=0x3f;
int mp[N][N];
int vis[N];
int dis[N];
int n,m,s;
void dijstra(int s)
{dis[s]=0;//vis[s]=1;while(1){int min_=INF,mini=0;for(int j=1;j<=n;j++){if(dis[j]<min_&&!vis[j])//寻找没有确定为最短路径的点{min_=dis[j];mini=j;}}if(mini==0){break;//没有找到就退出}vis[mini]=1;for(int i=1;i<=n;i++){if(dis[i]>dis[mini]+mp[mini][i]){dis[i]=dis[mini]+mp[mini][i];//依次进行松弛}}}
}
int main()
{memset(mp,INF,sizeof(mp));memset(dis,INF,sizeof(dis));cin>>n>>m>>s;int a,b,w;while(m--){cin>>a>>b>>w;mp[a][b]=min(mp[a][b],w);}dijstra(s);for(int i=1;i<=n;i++){cout<<dis[i]<<' ';}return 0;
}spfa算法：可以判断是否会存在负权边
例题
邻接矩阵版本（会MLE,只有60分）
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n,m,s;
const int N = 1e3+2;
const int INF=0x3f;
int mp[N][N];
queue<int> q;
int sum[N];
int dis[N],vis[N];
int cur;
void spfa(int s)
{q.push(s);vis[s]=1;dis[s]=0;while(!q.empty()){cur=q.front();q.pop();vis[cur]=0;for(int i=1;i<=n;i++){if(mp[cur][i]!=INF){if(dis[i]>dis[cur]+mp[cur][i]){dis[i]=dis[cur]+mp[cur][i];if(vis[i]!=1){q.push(i);vis[i]=1;/*sum[i]++;if(sum[i]>=n){cout<<"有负权回路"<<endl;}*/}}}}}}
int main()
{cin>>n>>m>>s;int a,b,w;memset(dis,INF,sizeof(dis));memset(mp,INF,sizeof(mp));for(int i=1;i<=m;i++){cin>>a>>b>>w;mp[a][b]=min(mp[a][b],w);}spfa(s);for(int i=1;i<=n;i++){cout<<dis[i]<<' ';}
}邻接表版
并查集
例题
无路径压缩版本
（会TLE）
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int n,m;
int f[100002];
int find_(int x)
{if(x!=f[x]){find_(f[x]);}elsereturn f[x];
}
int main()
{cin>>n>>m;char op;int a,b;for(int i=1;i<=n;i++){f[i]=i;}while(m--){cin>>op;cin>>a>>b;if(op=='M'){a=find_(a);b=find_(b);if(a!=b){f[a]=b;}}if(op=='Q'){if(find_(a)==find_(b)){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}}return 0;
}路径压缩版
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int n,m;
int f[100002];
int find_(int x)
{if(x==f[x]){return f[x];}else{f[x]=find_(f[x]);//这里return f[x];}}
void merge_(int a,int b)
{f[find_(a)]=find_(b);
}
int main()
{cin>>n>>m;char op;int a,b;for(int i=1;i<=n;i++){f[i]=i;}while(m--){cin>>op;cin>>a>>b;if(op=='M'){if(find_(a)!=find_(b))merge_(a,b);}if(op=='Q'){if(find_(a)==find_(b)){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}}return 0;
}一些注意事项
1.要记得 long long;
2.实现估算一下，如果循环次数超过10e8就要考虑进行优化，否则可能会TLE;
3.二维数组如果大于10e5可能会MLE,要考虑优化；
4.x%n的值为0到n-1；
5.EOF可以用不？
准备了近一个月。
尽人事，听天命吧。
事实证明，会这些基本的算法是不配参加蓝桥杯的 （赛后补充）
含泪捐了300元
附大佬总结的2016年真题
相关文章：
准备2023（2024）蓝桥杯
前缀和 一维前缀和 s[i]s[i-1]a[i]二维前缀和（子矩阵的和） s[i][j]s[i-1][j]s[i][j-1]-s[i-1][j-1]a[i][j] 差分 一维数组 //b是差分数组b[i]c;b[j1]-c;例题 #include<iostream> using namespace std; int n,m; int b[100002],a[100002]; vo…...
剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数 难度：middle\color{orange}{middle}middle 题目描述 把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。 你需要用一个浮点数数组返回答案，其中第 i 个…...
阿里巴巴-淘宝搜索排序算法学习
模型效能：模型结构优化 模型效能：减枝 FLOPS：每秒浮点运算的次数 模型效能：量化 基于统计阈值限定，基于学习阈值限定。 平台效能：一站式DL训练平台 平台效能：搜索模型的系统流程 协同关系…...
〖Python网络爬虫实战⑮〗- pyquery的使用
订阅：新手可以订阅我的其他专栏。免费阶段订阅量1000python项目实战 Python编程基础教程系列（零基础小白搬砖逆袭) 说明：本专栏持续更新中，目前专栏免费订阅，在转为付费专栏前订阅本专栏的，可以免费订阅付费…...
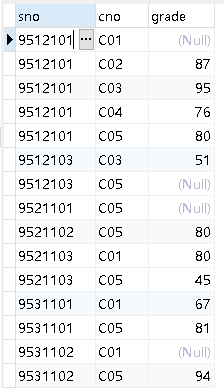
SQL综合查询下
SQL综合查询下 目录SQL综合查询下18、查询所有人都选修了的课程号与课程名题目代码题解19、SQL查询：查询没有参加选课的学生。题目代码20、SQL查询：统计各门课程选修人数，要求输出课程代号，课程名，有成绩人数ÿ…...
全连接层FC
lenet结构： 输入层（Input Layer）：接收手写数字的图像数据，通常是28x28的灰度图像。 卷积层1（Convolutional Layer 1）：对输入图像进行卷积操作，提取低级别的特征，使用 6 个大小为 5x5 的卷积核进行卷积，得到 6 个输出特征图，激活函数为 Sigmoid。 平均池化层1（Aver…...
图的遍历及连通性
文章目录 图的遍历及连通性程序设计程序分析图的遍历及连通性 【问题描述】 根据输入的图的邻接矩阵A，判断此图的连通分量的个数。 【输入形式】 第一行为图的结点个数n，之后的n行为邻接矩阵的内容，每行n个数表示。其中A[i][j]=1表示两个结点邻接，而A[i][j]=0表示两个结点无…...
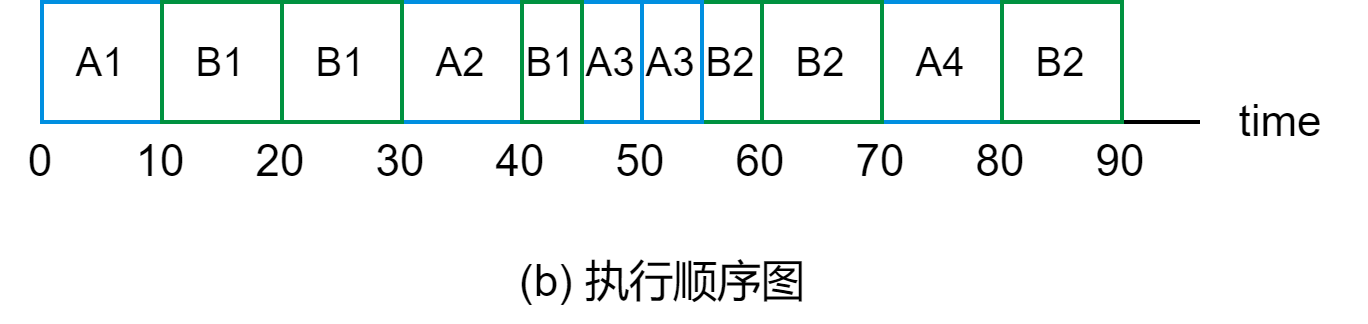
DJ3-4 实时调度
目录 3.4.1 实现实时调度的基本条件 1. 提供必要的信息 2. 系统的处理能力强 3. 采用抢占式调度机制 4. 具有快速切换机制 3.4.2 实时调度算法的分类 1. 非抢占式调度算法 2. 抢占式调度算法 3.4.3 常用的几种实时调度算法 1. 最早截止时间优先 EDF（Ea…...
Oracle之PL/SQL游标练习题（三）
游标练习题目1、定义游标：列出每个员工的姓名部门名称并编程显示第10个到第20个记录2、定义游标：从雇员表中显示工资大于3000的记录，只要姓名、部门编号和工资，编程显示其中的奇数记录3、用游标显示所有部门编号与名称，…...
docker运行服务端性能监控系统Prometheus和数据分析系统Grafana
文章目录一、Prometheus的安装和运行1、使用docker拉取镜像2、创建prometheus.yml文件3、启动容器4、查看启动是否成功5、记录安装过程中出现的错误二、Grafana的安装和运行1、使用docker拉取镜像2、创建grafana3、运行grafana4、查看grafana运行日志5、登录grafana一、Prometh…...
【Linux】【应用层】多线程编程
一、线程创建 Linux 中的 pthread_create() 函数用来创建线程，它声明在<pthread.h>头文件中，语法格式如下： int pthread_create(pthread_t *thread,const pthread_attr_t *attr,void *(*start_routine) (void *),void *arg);各个参数…...
GameFramework 框架详解之 如何接入热更框架HybridCLR
一.前言 HybridCLR是一个特性完整、零成本、高性能、低内存的近乎完美的c#热更新方案 GameFramework是一个非常出色完整的基于Unity引擎的游戏框架，里面包含了非常多的模块，封装非常完整。 以前市面上的热更大多数都是Lua为主，后来出了一个ILRuntime的C#热更框架，虽然性能…...
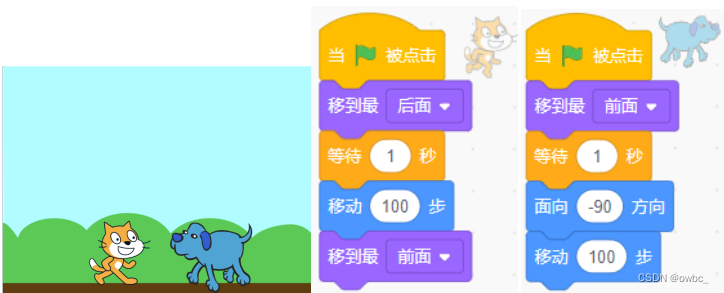
全国青少年软件编程(Scratch)等级考试二级考试真题2023年3月——持续更新.....
一、单选题(共25题，共50分) 1. 小猫的程序如图所示，积木块的颜色与球的颜色一致。点击绿旗执行程序后，下列说法正确的是？（ ） A.小猫一直在左右移动，嘴里一直说着“抓到了”。 B.小猫会碰到球，然后停止。 C.小猫一直在左右移动，嘴里一直说着“别跑” D.小猫会碰到球，…...
HTML2.1列表标签
列表标签种类 无序列表 有序列表 自定义列表 使用场景：在列表中按照行展示关联性内容。 特点：按照行的形式，整齐显示内容。 一、无序列表 标签名说明ul无序列表整体，用于包裹li标签li表示无序列表的每一项，用于包…...
在 Flutter 多人视频通话中实现虚拟背景、美颜与空间音效
前言 在之前的「基于声网 Flutter SDK 实现多人视频通话」里，我们通过 Flutter 声网 SDK 完美实现了跨平台和多人视频通话的效果，那么本篇我们将在之前例子的基础上进阶介绍一些常用的特效功能，包括虚拟背景、色彩增强、空间音频、基础变声…...
Ambari-web 架构
Ambari-web 使用的前端 Embar.js MVC 框架实现，Embar.js 是一个 TodoMVC 框架，涵盖了单页面应用（single page application）几乎所有的行为 Nodejs 是一个基于 Chrome JavaScript 运行时建立的一个平台，用来方便的搭建…...
对接百思买Best Buy EDI 的注意事项
在此前的文章：《Best Buy Drop Ship(Commerce hub) EDI业务测试常见报错及解决》中，我们介绍了在业务测试过程中遇到的常见报错及解决方案，以下在此基础上进行补充。 数据未能成功发送给Best Buy可能遇到的情况 Best Buy EDI项目传输业务报…...
2023年郑州重点建设项目名单公布，中创“算力数据中心”项目入选！
4月7日，郑州市人民政府网站公布2023年郑州市重点建设项目名单，名单共列项目680个，总投资1.08万亿元，年度计划投资2691亿元。 在创新驱动能力提升项目名单里，中创算力与人民网人民数据（国家大数据灾备中心&a…...
Pytorch 容器 - 1. Module类介绍
目录 1. 基于Module构建自己的网络 2. Module的初始化变量 3. Modules中需要子类 forward() 4. Modules中其他内置函数 1. 基于Module构建自己的网络 torch.nn.Module是所有神经网络模块的基类，如何定义自已的网络： 由于 Module 是神经网络模块的基…...
百度墨卡托坐标转化笔记
一、墨卡托坐标转化 调研了python和java多种实现方式的转换，发现有的不符合需求，原因还没找到。 我是用百度地图返回的poi边界（返回的是墨卡托坐标） 转换的原理没有深入研究，直接拿来用的，测试可行&…...
每日学术速递4.12
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.HC 随着新的“生成代理”论文的发布，LLM刚刚达到了一个重要的里程碑——通过使用 LLM，生成代理能够在受《模拟人生》启发的交互式沙箱中模拟类人行为。代理架构扩展…...
HarmonyOS/OpenHarmony公司级技术开发团队硬件基本配置清单
有朋友公司咨询进入HarmonyOS/OpenHarmony领域，组建技术团队，硬件设备的基本配置应该是怎么样的比较合适？这个是进入鸿蒙开发领域相关配置的第一步，我们以一个基本的团队配置为例说明，供想进入的团队参考。 HarmonyOS/…...
新一代信息技术赋能，安科瑞搭建智慧水务体系的新思路
随着新时期治水方针的逐步落实，水利现代化、智能化建设已开启，物联网、图像识别、数字孪生等新技术的成熟，也为智慧水务体系的搭建提供了技术保障，新时代治水新思路正逐步得到落实。本文对智慧水务的总体架构与包含的建设内容进行…...
37岁测试工程师被裁，120天没找到工作，无奈...
从短期来看，程序员的确算是个不错的工作，薪水也比一般岗位高很多，但是从长远来看，程序员的中年危机会比其他岗位来的更早，很多程序员只有到了35岁左右，才能真正认清楚互联网行业，尤其是被裁之后…...
Java容器使用注意点
前置：问题 判空集合转map集合遍历集合去重集合转数组数组转集合 一：集合判空 《阿里巴巴 Java 开发手册》的描述如下： 判断所有集合内部的元素是否为空，使用 isEmpty() 方法，而不是 size()0 的方式。 我们在开发中也…...
密文题解（图论+字典树）
题目大意 有一段长度为nnn的密文，密文的每一位都可以用一个非负整数来描述，并且每一位都有一个权值aia_iai。你可以操作任意多次，每次操作可以选择任意一段密文，花费选择的所有位上权值的异或和的代价获得这段密文每一位的异或…...
Baumer工业相机堡盟工业相机如何通过BGAPISDK里的工具函数来计算工业相机的实时帧率（C#）
Baumer工业相机堡盟工业相机如何通过BGAPISDK里函数来计算相机的实时帧率（C#）Baumer工业相机Baumer工业相机的帧率的技术背景Baumer工业相机的帧率计算方式在BufferEvent声明显示FrameID设计显示帧率的函数Baumer工业相机通过BGAPI SDK计算帧率的优势B…...
数据结构与常量（Java）
目录 1.字面常量 2. 数据类型 3. 变量 3.1 变量概念 3.2 语法格式 补充：变量 int long short double和float char boolean byte 4.类型转换 类型提升小结 5. 字符串类型 1. int 转成 String 2. String 转成 int 1.字面常量 类似System.Out.p…...
【LeetCode】剑指 Offer 54. 二叉搜索树的第k大节点 p269 -- Java Version
题目链接：https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/ 1. 题目介绍（ 54. 二叉搜索树的第k大节点） 给定一棵二叉搜索树，请找出其中第 k 大的节点的值。 【测试用例】： 示例 1: 示例2&…...
[工具类] post请求 获取request对象, 获取request的请求体(body)参数
目录 引言: 1. 获取request对象的几种常用方式 -> 1.1 获取请求对象 通过请求上下文对象 获取信息[推荐] -> 1.2 在controller层直接获取[不推荐 侵害性太强] -> 1.3 interceptor中获取[部分业务中使用] -> 1.4 request常用api简介 2. 获取request的body的工具…...