【算法LearnNO.1】算法介绍以及算法的时间复杂度和空间复杂度
目录
一、算法
1、算法概述
2、算法的5个特性
3、设计算法的标准
二、时间复杂度
1、时间复杂度的介绍
2、渐进时间复杂度的求法
3、计算时间复杂度的代码举例(平方阶示例)
4、时间复杂度排序
三、空间复杂度
一、算法
1、算法概述
算法就是解决问题的方法。以数据结构来表示出来对于问题的解决方法。一般算法的表示有三种方法:①自然语言表示②程序代码③类C语言。
2、算法的5个特性
有穷性:算法的实现是通过又穷步就可完成,且每一步都是有穷时间内完成的。
确定性:算法实现的输出结果唯一,对于算法中的所要执行的操作有确切的规定,不会存在二义性。
可行性:所有操作在有限时间内可实现。
输入:一个算法有零个或多个输入。
输出:一个算法有一个或多个输出。
3、设计算法的标准
正确性:不单单是程序语法正确,还要在运行一些能涵盖所有情况的特殊数据后能够准确的得到及结构。
可读性:算法是给人看的,要让读者能够读懂,而不会在阅读中有很多看不明白的地方。多增加注释,在很多变量和语句中增加解释,让算法变得清晰。
健壮性:随机应变能力。当输入非法的数据时,不会乱七八糟的随意输出,而会做出正确的反应或者得到错误提醒的输出语句。
高效性:高效分为时间高效和空间高效。效率高,则时间短,所需空间小。但是有时候时间效率和空间效率是矛盾的,想要时间效率高有时候会消耗很大的空间。
二、时间复杂度
算法时间效率是依据程序在计算机上运行所消耗的时间来度量的。度量方法有事后统计和事前分析两种方法,而人们一般会用后者,在编写程序之前对算法所消耗资源进行估算。
1、时间复杂度的介绍
一个算法的运行时间是=每条语句的执行次数ⅹ该语句执行一次所需要的时间
for(i=0;i<n;i++){ //频度为n+1for(i=0;i<n;i++){ //频度为n*(n+1)k=k*2;}
}上面代码段的运行时间用含n的函数表示为f(n)=n²+2n+1,
上式函数的同阶函数为n²,
我们用"O"来表示数量级,则T(n)=O(f(n))=O(n²);T(n)即为上述算法的渐进时间复杂度,简称时间复杂度。
2、渐进时间复杂度的求法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
3、计算时间复杂度的代码举例(平方阶示例)
int x=0;y=0; for(k=1;k<=n;k++){x++;} for(i=1;i<=n;i++){for(j=1;j<=n;j++){y++; }}对循环语句只需考虑循环体中语句的执行次数,以上程序段中频度最大的语句是第(7)行,其频度为f(n)=n²,所以该算法的时间复杂度为T(n)=O(n²),称为平方阶。
笔者的理解是算法的时间复杂度是由最深层循环内的基本语句的频度f(n)决定的,最深处的语句就是频度最大的语句。
4、时间复杂度排序
时间复杂度T(n)按数量级递增顺序为(从左到右复杂度升高):

三、空间复杂度
时代发展,科技进步,人们都不是很关注空间的占用情况了,因为现在的计算机的存储空间都很大很大。
空间复杂度:算法所需存储空间(寄存器)的量度。
记作:S(n)=O(f(n))
算法所占用的空间包括:
①算法本身所占用的空间:输入输出以及定义的变量等所占用的空间。
②算法要使用的辅助空间。
笔者认为计算空间复杂度是注重在于寻找定义,因为变量是在定义的时候才会被分配空间,在程序中寻找总共分配了多少个空间给变量,空间复杂度就是多少,空间复杂度的差异取决于辅助空间的大小分配,辅助空间分配的多少就能间接的体现出来空间复杂度的大小。
值得注意的是:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
今天的分享就到这啦😉
如果我的文章对您有帮助,
希望可以 “点赞” “收藏” “关注” 一键三连支持一下哦!
想了解更多知识请前往故里♡927的博客
如果以上内容有什么问题,欢迎留言,大家一起学习,共同进步。
我们下期见😉~~
相关文章:

【算法LearnNO.1】算法介绍以及算法的时间复杂度和空间复杂度
目录 一、算法 1、算法概述 2、算法的5个特性 3、设计算法的标准 二、时间复杂度 1、时间复杂度的介绍 2、渐进时间复杂度的求法 3、计算时间复杂度的代码举例(平方阶示例) 4、时间复杂度排序 三、空间复杂度 一、算法 1、算法概述 算法就是解…...
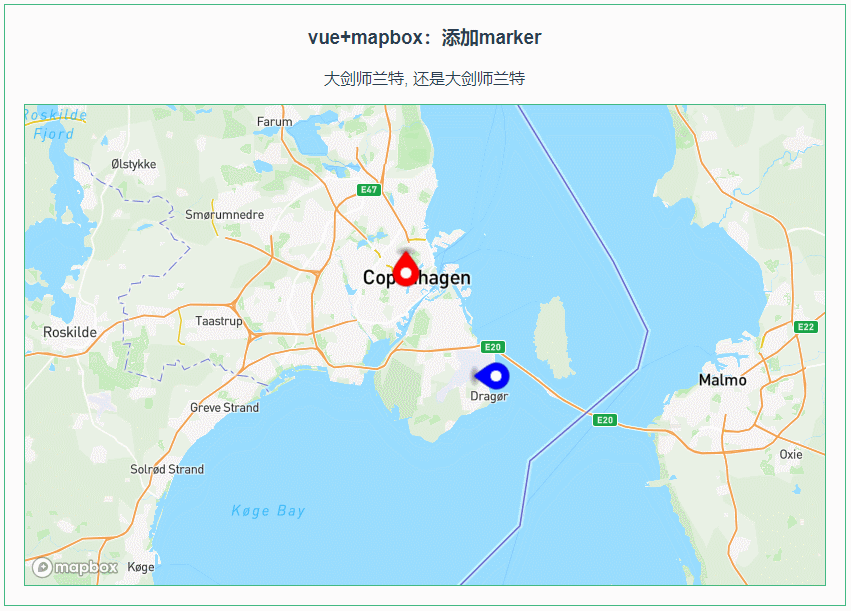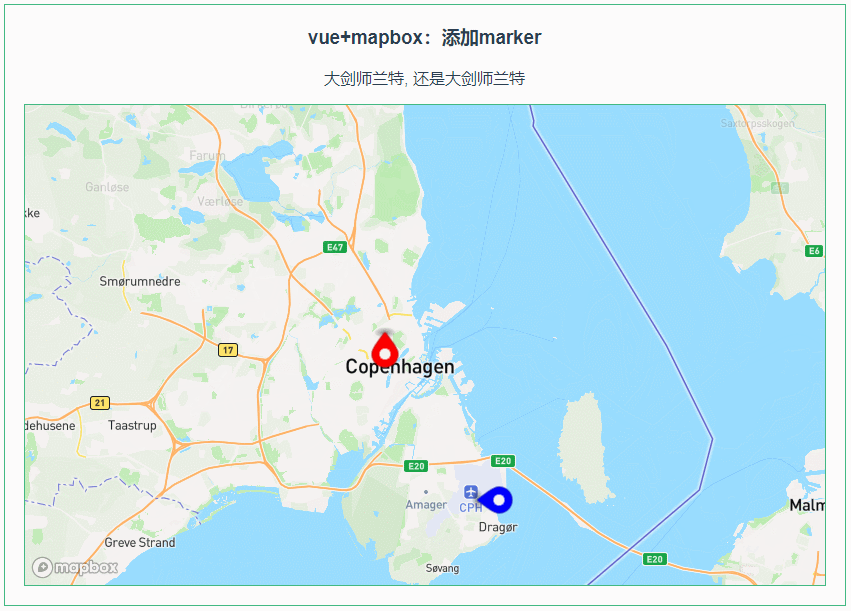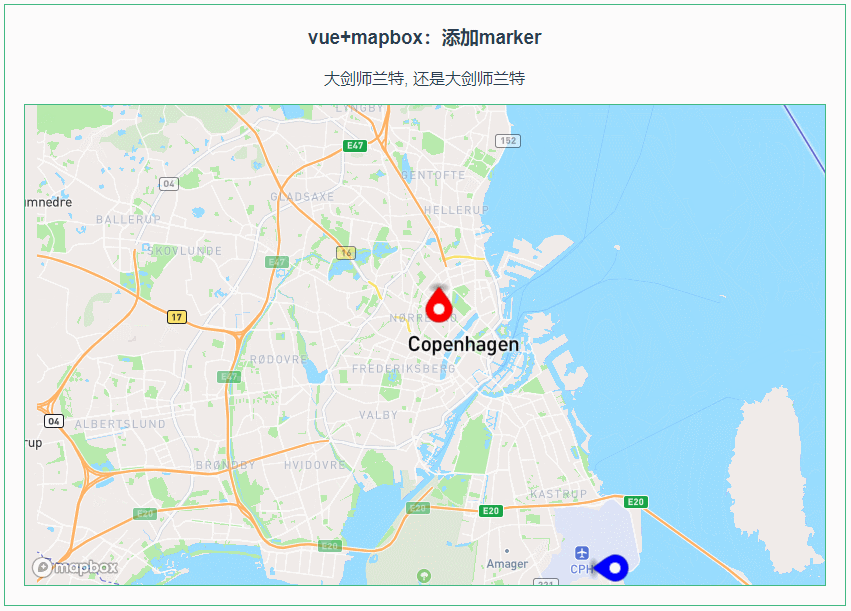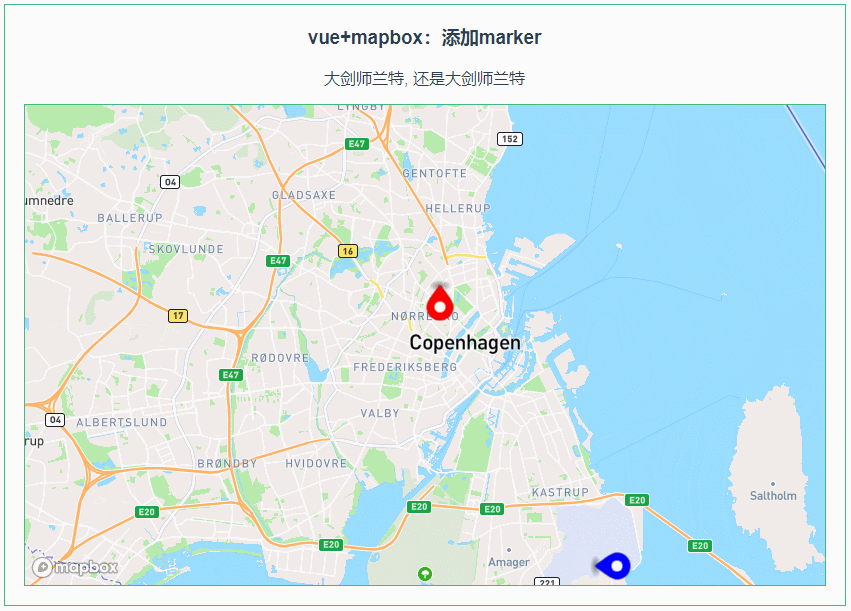
013:Mapbox GL添加marker
第013个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中添加marker。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共70行)相关API参考:专栏目标示例效果 配置方式 1)查看基础设置:https://xiaozhu…...

智慧工厂可视化合集,推动行业数字化转型
图扑软件基于 HTML5(Canvas/WebGL/WebVR)标准的 Web 技术,满足了工业物联网跨平台云端化部署实施的需求,以低代码的形式自由构建三维数字孪生、大屏可视化、工业组态等等。从 SDK 组件库,到 2D 和 3D 编辑,…...
工作流调度系统 Azkaban介绍与安装(一)
文章目录前言1、为什么要用工作流调度系统2、常见的工作流调度系统1 集群规划2 配置 MySQL3 配置 Executor Server3.1 修改 azkaban.properties3.2 启动3.3 激活4 配置 Web Server4.1 修改 azkaban.properties4.2 修改azkaban-users.xml文件,添加 atguigu 用户4.3 启…...
【Python基础入门学习】Python工具Pycharm的安装与使用
一、关于Python 1.1 下载Python 在下载与安装pycharm工具前,一定要先安装python 打开Python官网:python下载打开上述网站,选择 Downloads -> 系统 我是Windows系统,点击进入后,找到自己要安装的安装包以及想安装的…...
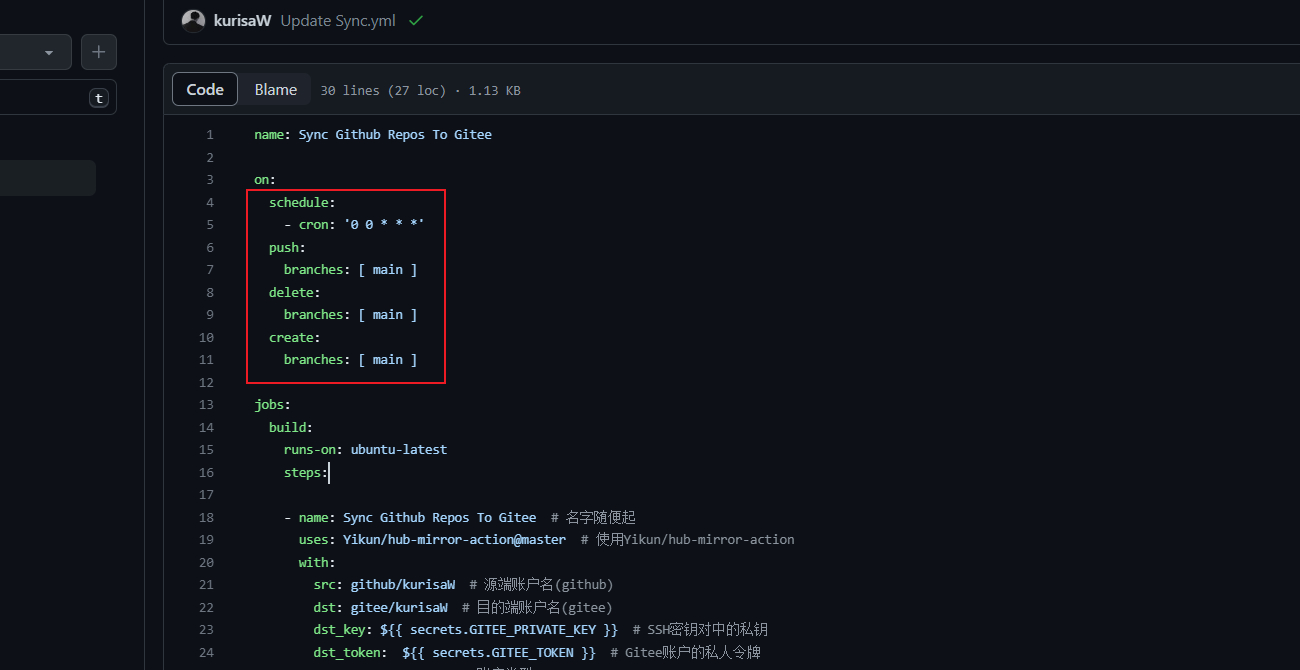
【版本控制】Github同步Gitee镜像仓库自动化脚本
文章目录Github同步Gitee镜像仓库自动化脚本前言什么是Hub Mirror Action?1.介绍2.用法配置步骤1.生成密钥对2.GitHub私钥配置3.Gitee公钥配置4.Gitee生成私人令牌5.Github绑定Gitee令牌6.编写CI脚本7.多仓库同步推送8.定时运行脚本总结Github同步Gitee镜像仓库自动…...

索引的分类
1.唯一索引 给表中某一列设置为了唯一约束(这列不允许出现重复数据)后,数据库会为将这一列设置索引,这个索引叫做唯一索引(主键那一列是一个特殊的唯一索引,不仅要满足唯一索引这一列不可以出现重复数据,而且这一列还…...

【整理九】
目录1.说说你对递归的理解?封装一个方法用递归实现树形结构封装2.Link和import有什么区别?3.什么是FOUC? 如何避免?4.说说你对预编译器的理解?5.shouldComponentUpdate 的作用6.概述下 React 中的事务处理逻辑7.React组件的划分业…...
钢网是SMT生产使用的一种工具,如何制作?
钢网是SMT生产使用的一种工具,其主要功能是将锡膏准确地涂敷在有需要焊接的PCB焊盘上。 钢网的好坏,直接影响印刷工作的质量,目前一般使用的金属钢网,是由薄薄的、带有小孔的金属板制作成的,在开孔处,锡膏…...

如何创建自己的gym环境
我们为什么要创建一个gym的环境呢?因为需要,哈哈哈,这是一句废话,但是也是一句真话。因为我不想自己写强化学习的算法了,我想用一些现成的框架,这些框架训练的都是gym的游戏,那我把我自己想要训…...

使用Marshaller 将Java对象转化为XML格式和字符串转为xml
使用Marshaller 将Java对象转化为XML格式 对象转xml内容 ①工具类 public static String convertObjectToXml(Object obj) throws Exception {StringWriter writer new StringWriter();// 创建 JAXBContext 和 MarshallerJAXBContext context JAXBContext.newInstance(obj.ge…...

NumPy 秘籍中文第二版:八、质量保证
原文:NumPy Cookbook - Second Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 “如果您对计算机撒谎,它将帮助您。” – Perry Farrar,ACM 通讯,第 28 卷 在本章中,我们将介绍以下秘籍: …...
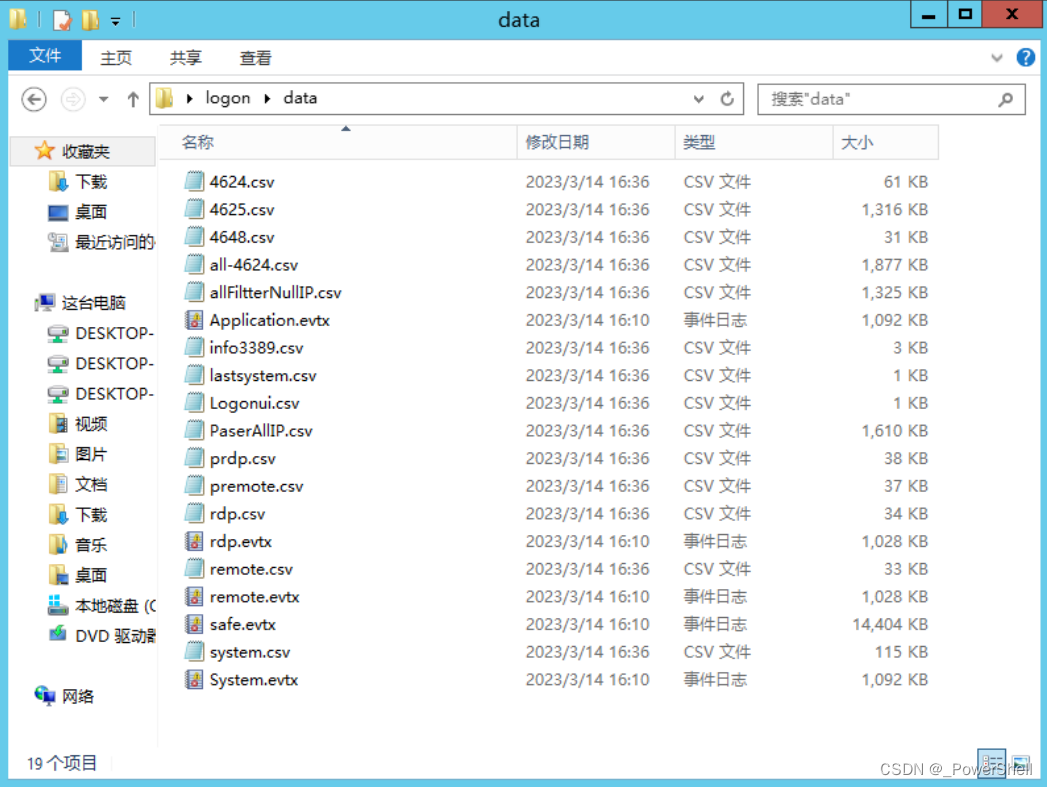
[ 应急响应篇基础 ] 日志分析工具Log Parser配合login工具使用详解(附安装教程)
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
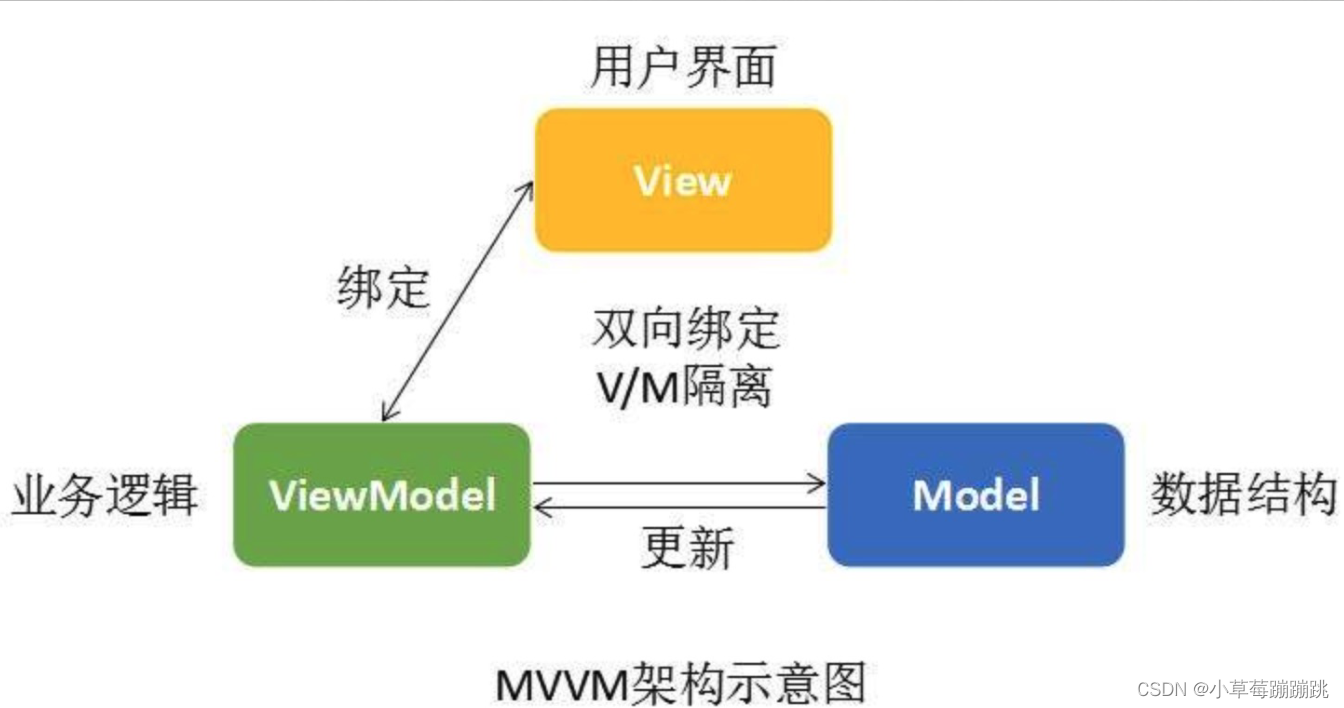
什么是MVVM?
MVVM 是 Model-View-ViewModel 的缩写,是M-V-VM三部分组成。它本质上就是MVC的改进版。 M:Model 代表数据模型,也可以在Model中定义数据修改和操作的业务逻辑。 V:View 代表视图UI,它负责将数据模型转化成UI 展现出来。…...

Java 企业电子招投标采购系统源码:采购过程更规范,更透明
满足采购业务全程数字化, 实现供应商管理、采购需求、全网寻源、全网比价、电子招 投标、合同订单执行的全过程管理。 电子招标采购,是指在网上寻源和采购产品和服务的过程。对于企业和企业主来说,这是个既省钱又能提高供应链效率的有效方法…...
)
1384:珍珠(bead)
1384:珍珠(bead) 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 有n颗形状和大小都一致的珍珠,它们的重量都不相同。n为整数,所有的珍珠从1到n编号。你的任务是发现哪颗珍珠的重量刚好处于正中间,即在所有珍珠的重量…...

34岁本科男,做了5年功能测试想转行,除了进厂还能干什么?
我的建议是不要给自己设限。任何一个行业只要做到顶尖都是很有作为的,何况是IT行业,本身就比别的行业有优势,如果你现在是功能测试,应该想的是进阶自动化测试或者测试开发 如何在半年时间由功能测试成长为年薪30W的测试开发&#…...
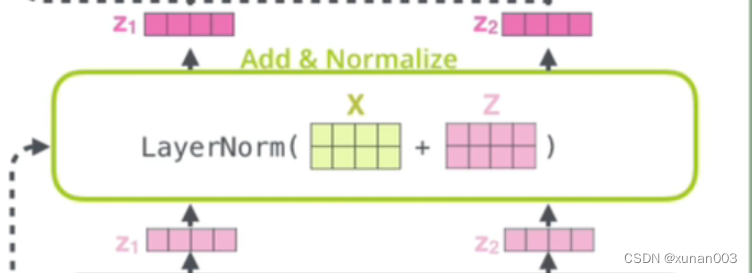
一文理解Transformer整套流程
【备注】部分图片引至他人博客,详情关注参考链接 【PS】query 、 key & value 的概念其实来源于推荐系统。基本原理是:给定一个 query,计算query 与 key 的相关性,然后根据query 与 key 的相关性去找到最合适的 value。举个例…...

04、SpringBoot运维实用篇
一、配置文件1、临时属性设置目前我们的程序包打好了,可以发布了。但是程序包打好以后,里面的配置都已经是固定的了,比如配置了服务器的端口是8080。如果我要启动项目,发现当前我的服务器上已经有应用启动起来并且占用了8080端口&…...

3.Java运算符
Java运算符 运算符基本分为六类:算数运算符、赋值运算符、关系运算符、逻辑运算符、位运算符、三元(条件)运算符。 一、算术运算符 算数运算符,是指在Java运算中,计算数值类型的计算符号,既然是操作数值…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
