数据结构——哈希表相关题目
数据结构——哈希表相关题目
- 242. 有效的字母异位词
- 1.暴力解法
- 2.排序后比较
- 3.哈希表
- 383. 赎金信
- 哈希解法
- 49. 字母异位词分组
- 438. 找到字符串中所有字母异位词
- 3. 无重复字符的最长子串
- 76. 最小覆盖子串
- 349. 两个数组的交集
- 1.排序+双指针
- 2.哈希表
- 350. 两个数组的交集 II
- 1.排序+双指针
- 2.哈希表
- 202. 快乐数
- 1.哈希表
- 2.快慢双指针
- 1. 两数之和
- 哈希表
- 454. 四数相加 II
- 哈希表
- 15. 三数之和
- 哈希解法
- 排序+双指针
242. 有效的字母异位词
242. 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true
示例 2: 输入: s = “rat”, t = “car” 输出: false
说明: 你可以假设字符串只包含小写字母。
1.暴力解法
两层for循环,同时记录字符是否重复出现,时间复杂度: O ( n 2 ) O(n^2) O(n2)
2.排序后比较
t 是 s 的异位词等价于「两个字符串排序后相等」。因此我们可以对字符串 s 和 t 分别排序,看排序后的字符串是否相等即可判断。此外,如果 s 和 t 的长度不同,t 必然不是 s 的异位词。
时间复杂度: O ( n log n ) O(n\log n) O(nlogn) 排序的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),比较两个字符串是否相等时间复杂度为 O ( n ) O(n) O(n)
空间复杂度: O ( log n ) O(\log n) O(logn) 排序需要 O ( log n ) O(\log n) O(logn) 的空间复杂度
class Solution {public boolean isAnagram(String s, String t) {if (s.length() != t.length()) {return false;}char[] str1 = s.toCharArray();char[] str2 = t.toCharArray();Arrays.sort(str1);Arrays.sort(str2);return Arrays.equals(str1, str2);}
}
3.哈希表
题目中字符串只有小写字符,那么就可以定义一个数组,来记录字符串s里字符出现的次数
定一个数组record,大小为26 ,初始化为0,因为字符a到字符z的ASCII也是26个连续的数值
字符串s= “aee”, t = “eae”

需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历 字符串s的时候,只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数,统计出来了。
检查字符串t中是否出现了这些字符,同样在遍历字符串t的时候,对t中出现的字符映射哈希表索引上的数值再做-1的操作。
最后检查,record数组如果有的元素不为零0,说明字符串s和t一定是谁多了字符或者谁少了字符,return false。
最后如果record数组所有元素都为零0,说明字符串s和t是字母异位词,return true。
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1),因为定义是的一个常量大小的辅助数组
class Solution {public boolean isAnagram(String s, String t) {int[] record = new int[26];for (char c : s.toCharArray()) {record[c-'a']++;}for (char c : t.toCharArray()) {record[c-'a']--;}for (int i : record) {if (i!=0)return false;}return true;}
}
383. 赎金信
383. 赎金信
给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串,判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成,返回 true ;否则返回 false。
(题目说明:为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)
注意:
你可以假设两个字符串均只含有小写字母。
canConstruct(“a”, “b”) -> false
canConstruct(“aa”, “ab”) -> false
canConstruct(“aa”, “aab”) -> true
暴力解法:两层for循环寻找
哈希解法
本题判断第一个字符串ransom能不能由第二个字符串magazines里面的字符构成,但是这里需要注意两点。
第一点:“为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思” 这里说明杂志里面的字母不可重复使用。
第二点: “你可以假设两个字符串均只含有小写字母。” 说明只有小写字母,这一点很重要
只有小写字母,那可以采用空间换取时间的哈希策略, 用一个长度为26的数组还记录magazine里字母出现的次数。
然后再用ransomNote去验证这个数组是否包含了ransomNote所需要的所有字母。
只需要满足字符串magazine 中的每个英文字母(’a’-’z’) 的统计次数都大于等于 ransomNote 中相同字母的统计次数即可
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
class Solution {public boolean canConstruct(String ransomNote, String magazine) {int[] record = new int[26];for (char c : magazine.toCharArray()) {// 通过recode数据记录 magazine里各个字符出现次数record[c-'a']++;}for (char c : ransomNote.toCharArray()) {// 遍历ransomNote,在record里对应的字符个数做--操作record[c-'a']--;// 如果小于零说明ransomNote里出现的字符,magazine没有if (record[c-'a']<0) return false;}return true;}
}
49. 字母异位词分组
49. 字母异位词分组
438. 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词
3. 无重复字符的最长子串
3. 无重复字符的最长子串
76. 最小覆盖子串
76. 最小覆盖子串
349. 两个数组的交集
349. 两个数组的交集
给定两个数组 nums1 和 nums2 ,返回它们的交集 。输出结果中的每个元素一定是唯一的。我们可以不考虑输出结果的顺序 。
1.排序+双指针
如果两个数组是有序的,则可以使用双指针的方法得到两个数组的交集。
首先对两个数组进行排序,然后使用两个指针遍历两个数组。可以预见的是加入答案的数组的元素一定是递增的,为了保证加入元素的唯一性,我们需要额外记录变量 pre 表示上一次加入答案数组的元素。
初始时,两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字,如果两个数字不相等,则将指向较小数字的指针右移一位,如果两个数字相等,且该数字不等于 pre ,将该数字添加到答案并更新 pre 变量,同时将两个指针都右移一位。当至少有一个指针超出数组范围时,遍历结束。
时间复杂度: O ( m log m + n log n ) O(m\log m + n\log n) O(mlogm+nlogn),其中 m 和 n 分别是两个数组的长度
空间复杂度: O ( log m + log n ) O(\log m + \log n) O(logm+logn),取决于排序使用的额外空间
class Solution {public int[] intersection(int[] nums1, int[] nums2) {Arrays.sort(nums1);Arrays.sort(nums2);int length1 = nums1.length, length2 = nums2.length;int[] intersection = new int[length1 + length2];int index = 0, index1 = 0, index2 = 0;while (index1 < length1 && index2 < length2) {int num1 = nums1[index1], num2 = nums2[index2];if (num1 == num2) {// 保证加入元素的唯一性if (index == 0 || num1 != intersection[index - 1]) {intersection[index++] = num1;}index1++;index2++;} else if (num1 < num2) {index1++;} else {index2++;}}return Arrays.copyOfRange(intersection, 0, index);}
}
2.哈希表
不需排序,不允许重复,选用HashSet。
时间复杂度: O ( m + n ) O(m + n) O(m+n),其中 m 和 n 分别是两个数组的长度
空间复杂度: O ( m + n ) O( m + n) O(m+n),取决于两个集合
class Solution {public int[] intersection(int[] nums1, int[] nums2) {if (nums1==null||nums2==null) {return new int[0];}Set<Integer> set = new HashSet<>();Set<Integer> resSet = new HashSet<>();for (int i : nums1) {//遍历数组1set.add(i);}for (int i : nums2) {//遍历数组2,判断哈希表中是否存在该元素if (set.contains(i))resSet.add(i);}int[] resArray = new int[resSet.size()];int index = 0;for (int i : resSet) {//将结果集合转为数组resArray[index++] = i;}return resArray;}
}
350. 两个数组的交集 II
350. 两个数组的交集 II
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
1.排序+双指针
与上一题类似,但不需要保证加入元素的唯一性。
时间复杂度: O ( m log m + n log n ) O(m\log m + n\log n) O(mlogm+nlogn),其中 m 和 n 分别是两个数组的长度
空间复杂度: O ( m i n ( m , n ) ) O( min(m,n)) O(min(m,n)),为返回值创建一个数组 intersection,其长度为较短的数组的长度
class Solution {public int[] intersect(int[] nums1, int[] nums2) {Arrays.sort(nums1);Arrays.sort(nums2);int length1 = nums1.length, length2 = nums2.length;int[] intersection = new int[Math.min(length1, length2)];int index1 = 0, index2 = 0, index = 0;while (index1 < length1 && index2 < length2) {if (nums1[index1] < nums2[index2]) {index1++;} else if (nums1[index1] > nums2[index2]) {index2++;} else {intersection[index] = nums1[index1];index1++;index2++;index++;}}return Arrays.copyOfRange(intersection, 0, index);}
}
2.哈希表
由于同一个数字在两个数组中都可能出现多次,因此需要用哈希表存储每个数字出现的次数,选用HashMap。对于一个数字,其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。
为了降低空间复杂度,首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数,然后遍历较长的数组得到交集

时间复杂度: O ( m + n ) O(m + n) O(m+n),其中 m 和 n 分别是两个数组的长度
空间复杂度: O ( m i n ( m , n ) ) O(min(m,n)) O(min(m,n)),对较短的数组进行哈希表的操作,哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组 intersection,其长度为较短的数组的长度。
class Solution {public int[] intersect(int[] nums1, int[] nums2) {HashMap<Integer,Integer> hashMap = new HashMap<>();//先把数组nums1元素存入哈希表中for (int i:nums1)hashMap.put(i,hashMap.getOrDefault(i,0)+1);//值为对应元素在nums1中出现的次数int[] ans = new int[Math.min(nums1.length, nums2.length)];int index = 0;for (int i = 0; i < nums2.length; i++) {if (hashMap.containsKey(nums2[i]) && hashMap.getOrDefault(nums2[i],0) > 0){//nums2[i]存于哈希表且哈希表中该元素数量不为0ans[index++] = nums2[i];hashMap.put(nums2[i],hashMap.get(nums2[i])-1);}}return Arrays.copyOf(ans,index);}
}
或不创建新数组,直接用nums1返回
class Solution {public int[] intersect(int[] nums1, int[] nums2) {Map<Integer,Integer> map = new HashMap<>();for (int i : nums1) {map.put(i,map.getOrDefault(i,0) + 1);}int index = 0;for (int j : nums2) {if (map.containsKey(j)){nums1[index++] = j;Integer count = map.get(j);if (count == 1){map.remove(j);}else {map.put(j,--count);}} }return Arrays.copyOfRange(nums1,0,index);}
}
进阶:
如果 nums2 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
如果 nums2的元素存储在磁盘上,磁盘内存是有限的,并且你不能一次加载所有的元素到内存中。那么就无法高效地对 nums2进行排序,因此推荐使用HashMap而不是排序+双指针。在方法2中,nums2只关系到查询操作,因此每次读取 nums2中的一部分数据,并进行处理即可。
202. 快乐数
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
示例:
输入:19
输出:true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
1.哈希表
可能出现无限循环,也就是说求和的过程中,sum会重复出现
使用哈希法,选用HashSet来判断这个sum是否重复出现,如果重复了就是return false, 否则一直找到sum为1为止
时间复杂度: O ( log n ) O(\log n) O(logn)
空间复杂度: O ( log n ) O(\log n) O(logn) ,与时间复杂度密切相关的是衡量我们放入哈希集合中的数字以及它们有多大的指标。对于足够大的 n,大部分空间将由 n 本身占用。我们可以很容易地优化到 O(243⋅3)=O(1),方法是只保存集合中小于 243 的数字,因为对于较高的数字,无论如何都不可能返回到它们。
class Solution {public boolean isHappy(int n) {Set<Integer> set = new HashSet<>();while (n!=1&&!set.contains(n)) {set.add(n);n = getSum(n);}//=1是快乐数,否则n重复,无限循环,falsereturn n==1;}int getSum(int n) {int sum = 0;while (n!=0) {int temp = n%10;sum += temp*temp;n /= 10;}return sum;}
}
2.快慢双指针
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next 指针是通过调用 getNext(n) 函数获得。
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环,如果重复了(成环)就是return false, 否则一直找到元素为1为止。
由快慢指针跟踪链表中的两个值。在算法的每一步中,慢指针在链表中前进 1 个节点,快指针前进 2 个节点(对 getNext(n) 函数的嵌套调用)。
-
如果 n 是一个快乐数,即没有循环,那么快指针最终会比慢指针先到达数字 1。
-
如果 n 不是一个快乐数,那么最终快指针和慢指针将在同一个数字上相遇。(快指针超过慢指针一圈)
时间复杂度: O ( log n ) O(\log n) O(logn)
时间复杂度: O ( 1 ) O(1) O(1)
class Solution {public boolean isHappy(int n) {int slow = n;int fast = getNext(n);while (fast!=1&&slow!=fast) {slow = getNext(slow);fast = getNext(getNext(fast));}return fast==1;}int getNext(int n) {int sum = 0;while (n!=0) {int temp = n%10;sum += temp*temp;n /= 10;}return sum;}
}
1. 两数之和
1. 两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
-
暴力解法:两层for循环, O ( n 2 ) O(n^2) O(n2)
-
两数之和 不能使用双指针法,因为两数之和要求返回的是索引下标, 而双指针法一定要排序,原数组是无序的,一旦排序之后原数组的索引就被改变了。
如果两数之和要求返回的是数值的话,就可以使用双指针法了。 -
数组无序时,考虑排序+双指针,或使用哈希表HashMap / HashSet 也可以帮助我们处理无序数组相关的简单问。、
哈希表
使用数组和set来做哈希法的局限:
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
此时就要选择另一种数据结构:Map ,map是一种key-value的存储结构,可以用key保存数值,用value在保存数值所在的下标。
寻找target-nums[i]的值是否在map的key中,找到则将该值和 i 一起存入数组中
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
class Solution {public int[] twoSum(int[] nums, int target) {int[] res = new int[2];if (nums==null||nums.length==0) return res;Map<Integer,Integer> map = new HashMap<>();for (int i=0;i<nums.length;i++) {int temp = target-nums[i];if (map.containsKey(temp)) {res[1] = i;res[0] = map.get(temp);}map.put(nums[i],i);}return res;}
}
170两数之和III
454. 四数相加 II
454. 四数相加 II
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ,使得 A[i] + B[j] + C[k] + D[l] = 0。
为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -2^28 到 2^28 - 1 之间,最终结果不会超过 2^31 - 1 。
例如:
输入: A = [ 1, 2] B = [-2,-1] C = [-1, 2] D = [ 0, 2] 输出: 2 解释: 两个元组如下:
1、(0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2、(1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0
哈希表
这道题目是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况,所以相对于题目18. 四数之和,题目15.三数之和,还是简单了不少
- 首先定义 一个HashMap,key放a和b两数之和,value放a和b两数之和出现的次数。
- 遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到map中。
- 定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
- 在遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
- 最后返回统计值 count 就可以了
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( n 2 ) O(n^2) O(n2),哈希映射需要使用的空间。在最坏的情况下,A[i]+B[j] 的值均不相同,因此值的个数为 n^2
class Solution {public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {Map<Integer,Integer> map =new HashMap<>();int temp,res = 0;//统计两个数组中的元素之和,同时统计出现的次数,放入mapfor (int i : nums1) {for (int j : nums2) {temp = i+j;if (map.containsKey(temp)) {map.put(temp,map.get(temp)+1);} else {map.put(temp,1);}}}//统计剩余的两个元素的和,在map中找是否存在相加为0的情况,同时记录次数for (int i :nums3) {for (int j : nums4) {temp = i+j;if (map.containsKey(-temp)) {res += map.get(-temp);}}}return res;}
}
15. 三数之和
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
哈希解法
这道题目使用哈希法并不十分合适
两层for循环就可以确定 a 和b 的数值了,可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过,思路是正确的,但是注意不可以包含重复的三元组。
把符合条件的三元组放进vector中,然后再去重,这样是非常费时的,很容易超时。去重的过程不好处理。时间复杂度可以做到 O ( n 2 ) O(n^2) O(n2),但还是比较费时的,因为不好做剪枝操作。
排序+双指针
首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i]、 b = nums[left] 、c = nums[right]。
如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
class Solution {public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(nums);for (int i=0;i<nums.length;i++) {//排序之后若第一个元素已经大于零,无论如何组合都不可能凑成三元组if (nums[i]>0) {return res;}// 错误去重方法,将会漏掉-1,-1,2 这种情况/*if (nums[i] == nums[i + 1]) {continue;}*/if (i>0&&nums[i]==nums[i-1]) {//正确去重continue;}int left = i+1;int right = nums.length-1;while (right>left) {//去重复逻辑如果放在这里,0,0,0 的情况,可能直接导致 right<=leftint sum = nums[i]+nums[left]+nums[right];if (sum>0) {right--;}else if (sum<0){left++;}else {res.add(Arrays.asList(nums[i],nums[left],nums[right]));// 去重逻辑应该放在找到一个三元组之后while(right>left&&nums[right]==nums[right-1]) right--;while(right>left&&nums[left]==nums[left+1]) left++;//找到答案时,双指针同时收缩left++;right--;}}}return res;}
}
相关文章:

数据结构——哈希表相关题目
数据结构——哈希表相关题目 242. 有效的字母异位词1.暴力解法2.排序后比较3.哈希表 383. 赎金信哈希解法 49. 字母异位词分组438. 找到字符串中所有字母异位词3. 无重复字符的最长子串76. 最小覆盖子串349. 两个数组的交集1.排序双指针2.哈希表 350. 两个数组的交集 II1.排序双…...
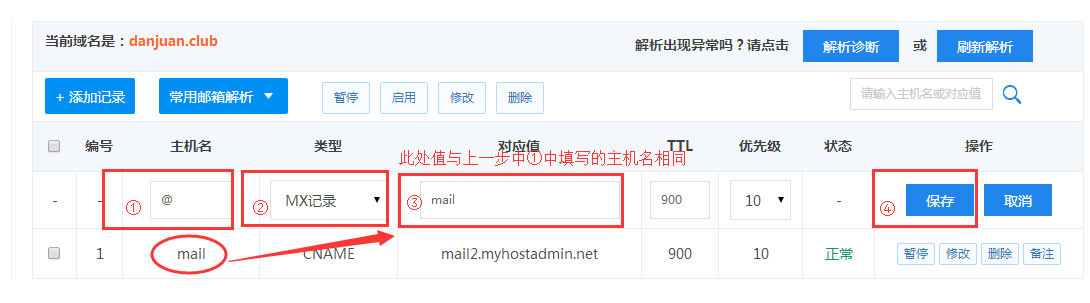
域名解析设置方法
域名解析设置都是实时生效的,一般只需几秒即可同步到各地 DNS 上,但各地 DNS 均有缓存机制,解析的最终生效取决于各运营商刷新时间! 一、A记录 ①.主机名必须填写; 常用主机名有:www//*,效果参见上图说明&…...

MySQL连接空闲时间超过8小时报错原因与延伸知识
1 错误原因 1.1 两个参数 MySQL服务端两个参数控制连接超时时间: wait_timeoutinteractive_timeout1.1.1 如何查看 show global variables like interactive_timeout show global variables like wait_timeout 复制代码 1.1.2 含义与区别 wait_timeout…...
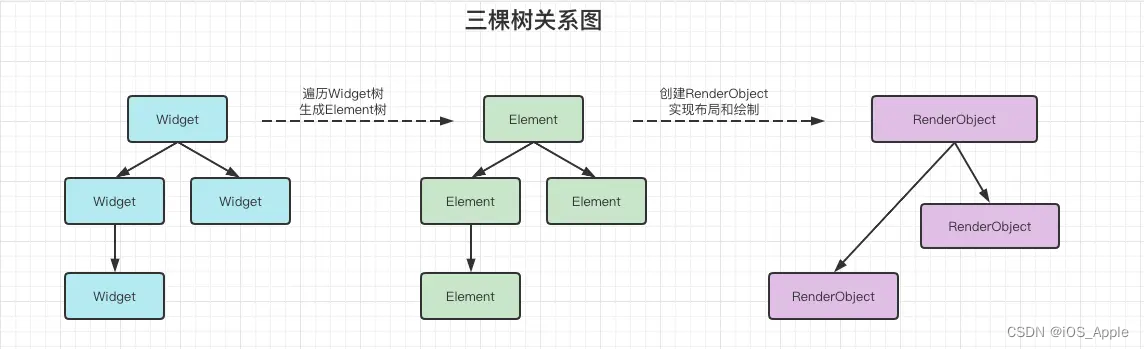
Flutter渲染原理
一 Widget Element RenderObject 之间的关系 1 Widget 在Flutter 中,万物皆是Widget,无论是可见的还是功能型的。一切都是Widget. 官方文档中说的Widget 使用配置和状态来描述View 界面应该长什么样子。 它不仅可以表示UI元素,也可以表示一些功能性的…...
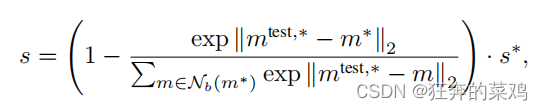
PathCore:IAD文献解读
论文链接:[Towards Total Recall in Industrial Anomaly Detection]Towards Total Recall in Industrial Anomaly Detection :数据集, :标签 : 在ImageNet上预训练后的网络 第 张图 网络中第 层 1. Locall…...

C语言判断一个日期是在该年的第几天案例讲解
今天是2023年4月11号,我们就用今天举例得出是2023年的第几天。 思路分析 1)我们想知道2023年4月11号是2023年的第几天,只需要把1到3月份的天数累加求和然后加上今天日期也就是11就可以算出2023年4月11号是2023年的第几天。 推广:…...

【超全总结】集成环信消息推送注意事项(华为、oppo、vivo等)
环信即时通讯 IM 支持集成第三方厂商的消息推送服务,为 Android 开发者提供低延时、高送达、高并发、不侵犯用户个人数据的离线消息推送服务。 当客户端应用进程被关闭等原因导致用户离线,环信即时通讯 IM 服务会通过第三方厂商的消息推送服务向该离线用…...

C++回调函数以及epoll中回调函数的使用
回调函数是一种常用的编程技术,它允许程序在运行时将一个函数作为参数传递给另一个函数,以实现更加灵活和可扩展的功能。在C中,回调函数通常被实现为函数指针或者函数对象。 函数指针是指向函数的指针变量,可以通过它来调用函数。…...
0基础学习软件测试有哪些建议
其实现在基础的资料和视频到处都是,就是看你有没有认真的去找学习资源了,去哪里学习都是要看你个人靠谱不靠谱,再好的教程和老师,你自己学习不进去也是白搭在正式选择之前,大可以在各种学习网站里面找找学习资源先自己…...
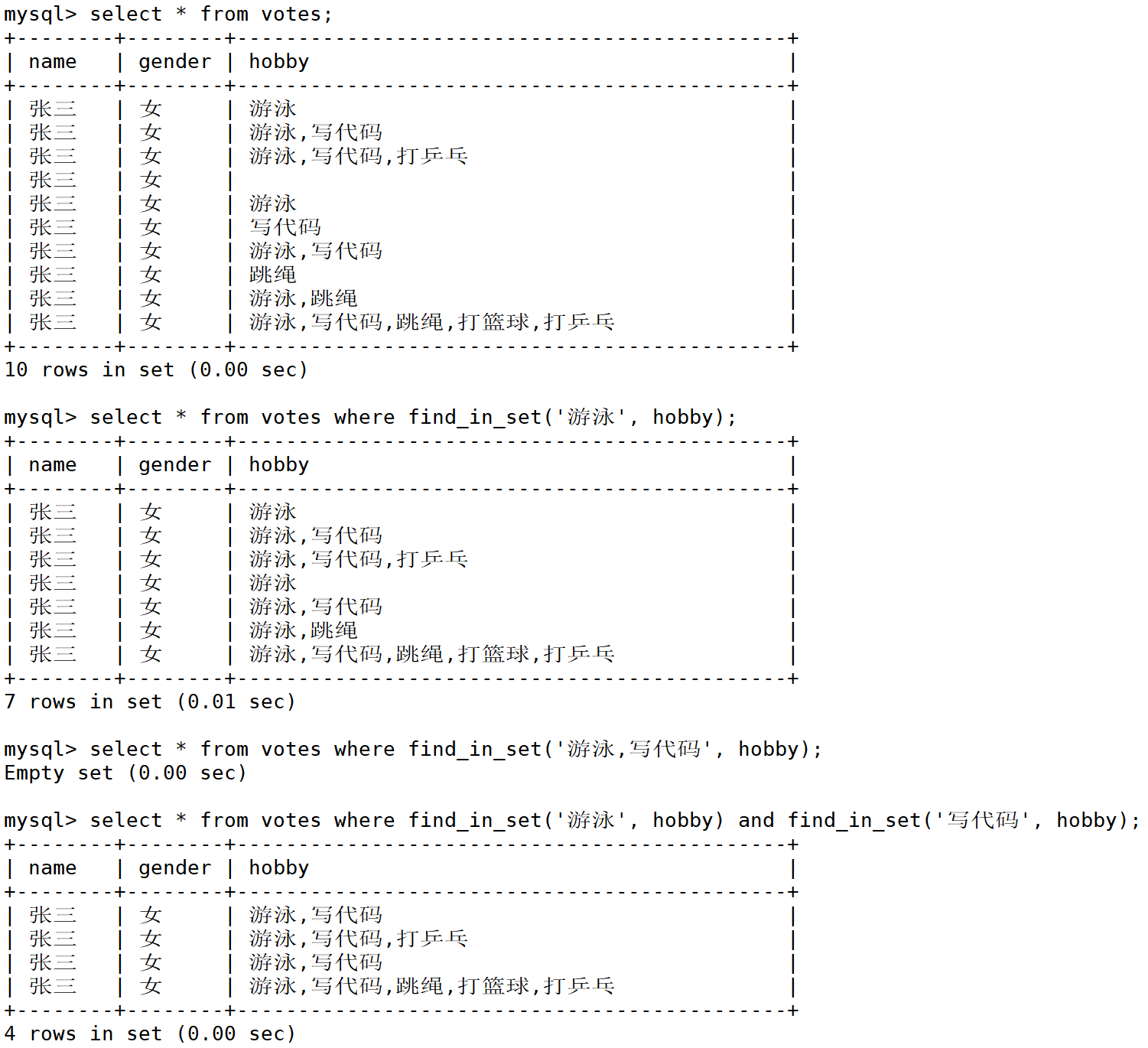
MySQL数据类型
文章目录一、数据类型分类二、数值类型1. tinyint 类型2. bit 类型3. int 类型4. float 类型5. decimal 类型三、字符串类型1. char 类型2. varchar 类型3. char 和 varchar 比较4.日期和时间类型5. enum 和 set一、数据类型分类 数据类型本质也是一种约束! 如果插入…...
【设计模式】从Mybatis源码中学习到的10种设计模式
文章目录 一、前言二、源码:学设计模式三、类型:创建型模式1. 工厂模式2. 单例模式3. 建造者模式 四、类型:结构型模式1. 适配器模式2. 代理模式3. 组合模式4. 装饰器模式 五、类型:行为型模式1. 模板模式2. 策略模式3. 迭代器模式…...

爬虫攻守道 - 猿人学第20题 - 殊途同归
写在开头 这题也是,自己搞顶多追踪到wasm代码,然后就走不下去了。找了2个参考方案,自己做的过程中还又遇到些新的问题,下面做个记录。解法1参考文章解法2参考文章 解法1:追根溯源 在 JS 代码中追踪到 Payload 赋值位…...

4.11日报
synchronized 和 ReentrantLock 区别是什么? synchronized 早期的实现比较低效,对比 ReentrantLock,大多数场景性能都相差较大,但是在 Java 6 中对 synchronized 进行了非常多的改进。 主要区别如下: ReentrantLock …...

【LeetCode每日一题: 1039. 多边形三角剖分的最低得分 | 暴力递归=>记忆化搜索=>动态规划 | 区间dp 】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...
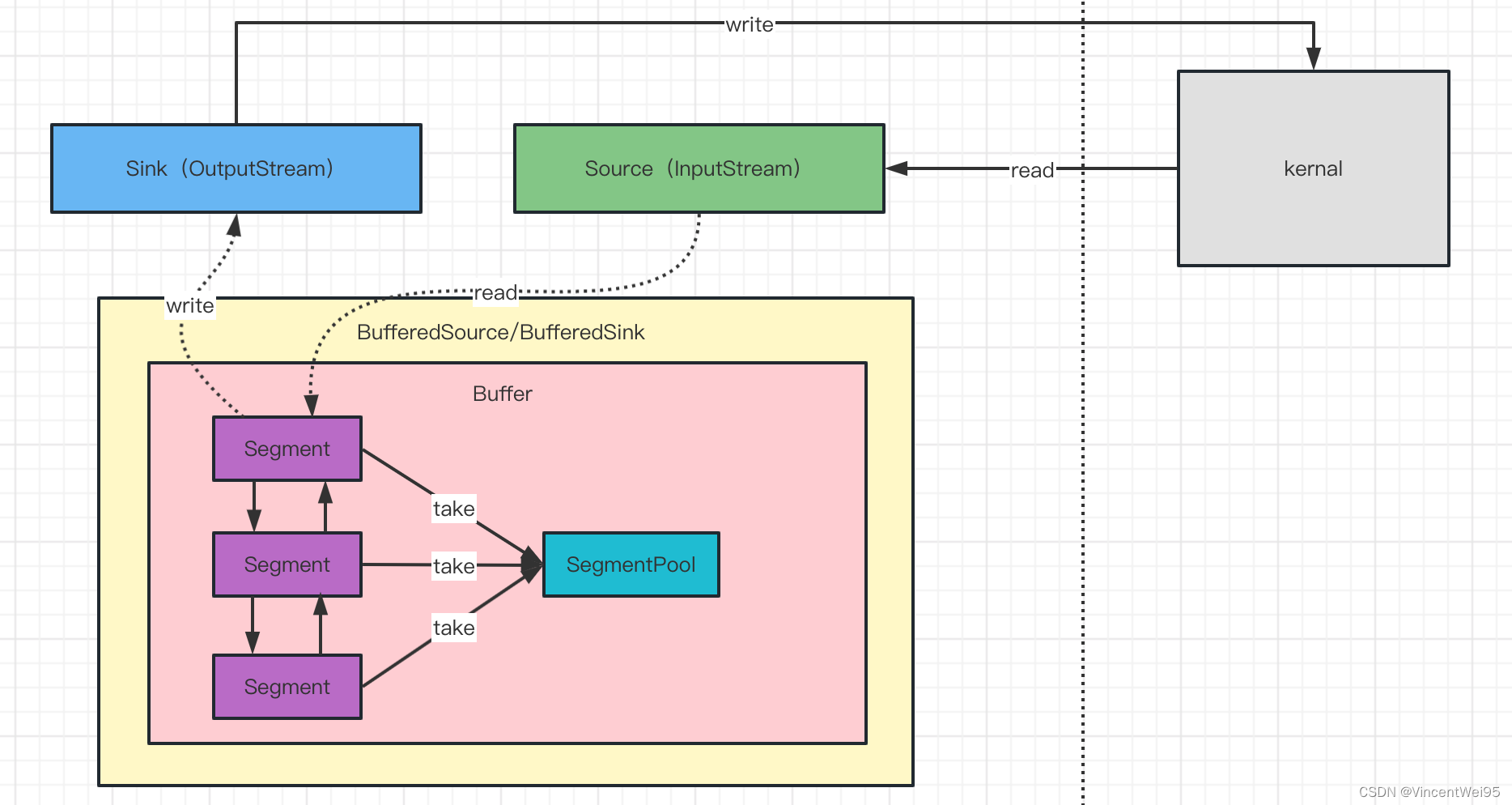
Okio 网络提速
文章目录网络数据处理流程Page Cache传统 I/O 拷贝的性能问题零拷贝技术DMA 技术零拷贝技术分类mmapsendfilespliceDirect I/O零拷贝技术性能分析小结OkioOkio 的使用Okio 网络提速的原理Okio 总结总结网络数据处理流程 在讲 Okio 之前,为了能更好的了解 Okio 的优…...

自动驾驶企业面临哪些数据安全挑战?
近期,“特斯拉员工被曝私下分享用户隐私”不可避免地成了新闻热点,据说连马斯克也不能幸免。 据相关媒体报道,9名前特斯拉员工爆料在2019年至2022年期间,特斯拉员工通过内部消息系统私下分享了一些车主车载摄像头记录的隐私视频和…...

Doris(2):Doris编译部署
1 Doris编译 Apache Doris提供直接可以部署的版本压缩包:https://cloud.baidu.com/doc/PALO/s/Ikivhcwb5 也可以自行编译压缩包后使用(推荐) 1.1 使用 Docker 开发镜像编译(推荐) 这个是官方文档推荐的,…...
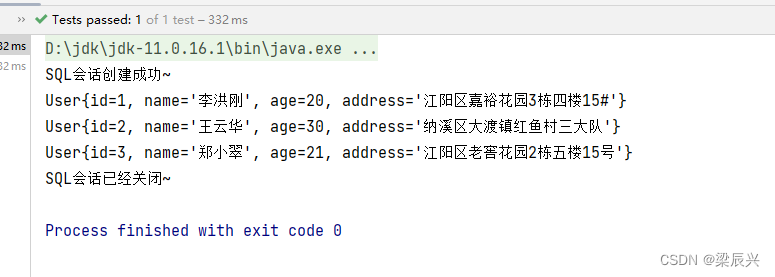
使用MyBatis实现简单查询
文章目录一,创建数据库与表(一)在Navicat里创建MySQL数据库testdb(二)创建用户表 - t_user(三)在用户表里插入3条记录二,案例演示MyBatis基本使用(一)创建Mav…...
[4]和char *point[4])
C指针(*point)[4]和char *point[4]
char (*point)[4] // 数组指针。 a[3][4] // 先申明二维数组,用它来指向这个二维数组. char *point[4] // 指针数组。 a[4][5] // 一连串的指针. char (*point)[4] // 一个指针,指向有4个元素的数组;占内存大小为 4 个字节 ch…...
【Bard】谷歌的人工智能工具—Bard初体验
文章目录一、Bard介绍二、Bard体验1、加入Bard的候补名单2、登入Bard篇3、使用Bard篇(1)提供三种预选方式✨(2)创作生成各类文案(3)无生成图画能力(4)支持语音转文本输入✨ÿ…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
