【LeetCode每日一题: 1039. 多边形三角剖分的最低得分 | 暴力递归=>记忆化搜索=>动态规划 | 区间dp 】

🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🍎座右铭:人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯🎯

目录
- 题目链接
- 题目描述
- 求解思路&实现代码&运行结果
- 暴力递归
- 求解思路
- 实现代码
- 运行结果
- 记忆化搜索
- 求解思路
- 实现代码
- 运行结果
- 动态规划
- 求解思路
- 实现代码
- 运行结果
- 共勉
题目链接
1039. 多边形三角剖分的最低得分
题目描述
你有一个凸的 n 边形,其每个顶点都有一个整数值。给定一个整数数组 values ,其中 values[i] 是第 i 个顶点的值(即顺时针顺序)。
假设将多边形剖分为 n - 2 个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。
返回多边形进行三角剖分后可以得到的最低分 。
示例 1:

输入:values = [1,2,3]
输出:6
解释:多边形已经三角化,唯一三角形的分数为 6。
示例 2:
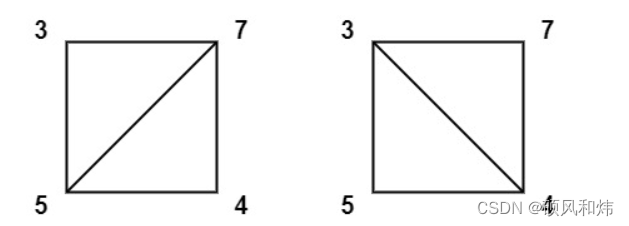
输入:values = [3,7,4,5]
输出:144
解释:有两种三角剖分,可能得分分别为:375 + 457 = 245,或 345 + 347 = 144。最低分数为 144。
示例 3:
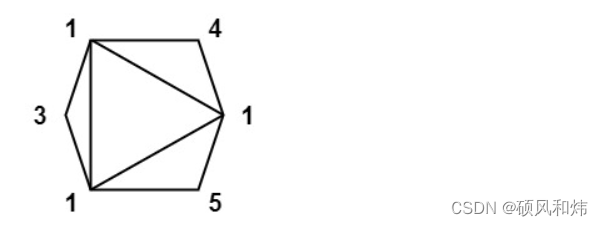
输入:values = [1,3,1,4,1,5]
输出:13
解释:最低分数三角剖分的得分情况为 113 + 114 + 115 + 111 = 13。
提示:
n == values.length
3 <= n <= 50
1 <= values[i] <= 100
求解思路&实现代码&运行结果
暴力递归
求解思路
- 为了能够让同学们更好的理解这个过程,我特意将整个思考的过程以及作图的过程都绘制在下面这张图中,希望可以通过下面这张图更好的帮助你理解整个过程,大家可以结合这张图来理解整个题目的求解思路。

实现代码
注意,代码的实现方式可以有很多,大家根据自己的习惯来就好
class Solution {public int minScoreTriangulation(int[] values) {int n = values.length;return dfs(0, n - 1,values);}private int dfs(int left, int right,int[] values) {if (left + 1 >= right) return 0;int min = Integer.MAX_VALUE;for (int k = left+1; k < right; k++){min = Math.min(min, dfs(left, k,values) + dfs(k, right,values) + values[left] * values[right] * values[k]);}return min;}
}
运行结果
大家不要看到时间超限就害怕,相反,看到这个我们更应该放心,使我们期待的结果。
记忆化搜索
求解思路
- 核心思路就是我们上面的求解过程,如果没有理解可以继续看上面的图解过程。
- 在原来的基础上加缓存表,将结果进行记录,避免重复计算。
实现代码
class Solution {public int minScoreTriangulation(int[] values) {int n = values.length;int[][] dp=new int[n][n];for(int i=0;i<n;i++) Arrays.fill(dp[i],-1);return dfs(0, n - 1,values,dp);}private int dfs(int left, int right,int[] values,int[][] dp) {if (left + 1 >= right) return dp[left][right]=0;if(dp[left][right]!=-1) return dp[left][right];int min = Integer.MAX_VALUE;for (int k = left+1; k < right; k++){min = Math.min(min, dfs(left, k,values,dp) + dfs(k, right,values,dp) + values[left] * values[right] * values[k]);}return dp[left][right]=min;}
}
运行结果
加个缓存表就是香,通过!
动态规划
求解思路
- 同理,核心求解思路我们上面已经讲过了,此处不同的是原来通过递归,此时我们通过dp数组和循环即可完成。
实现代码
继续改进!
class Solution {public int minScoreTriangulation(int[] values) {int n = values.length;int[][] dp=new int[n][n];for(int left=n-3;left>=0;left--){for(int right=left+2;right<n;right++){int min = Integer.MAX_VALUE;for (int k = left+1; k < right; k++){min = Math.min(min, dp[left][k] + dp[k][right] + values[left] * values[right] * values[k]);}dp[left][right]=min;}}return dp[0][n - 1];}
}
}
运行结果
共勉
最后,我想送给大家一句一直激励我的座右铭,希望可以与大家共勉!


相关文章:

【LeetCode每日一题: 1039. 多边形三角剖分的最低得分 | 暴力递归=>记忆化搜索=>动态规划 | 区间dp 】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...
Okio 网络提速
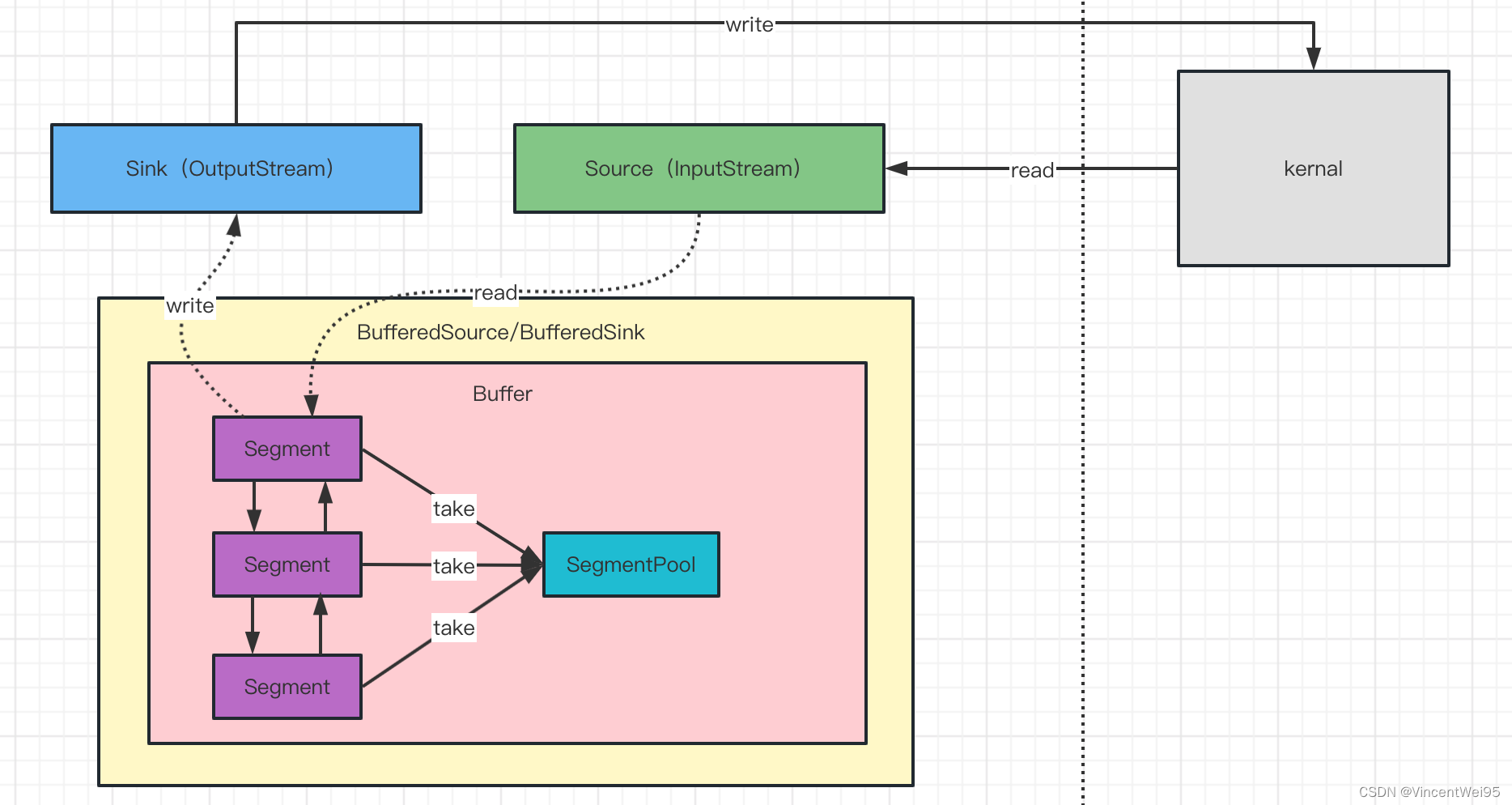
文章目录网络数据处理流程Page Cache传统 I/O 拷贝的性能问题零拷贝技术DMA 技术零拷贝技术分类mmapsendfilespliceDirect I/O零拷贝技术性能分析小结OkioOkio 的使用Okio 网络提速的原理Okio 总结总结网络数据处理流程 在讲 Okio 之前,为了能更好的了解 Okio 的优…...

自动驾驶企业面临哪些数据安全挑战?
近期,“特斯拉员工被曝私下分享用户隐私”不可避免地成了新闻热点,据说连马斯克也不能幸免。 据相关媒体报道,9名前特斯拉员工爆料在2019年至2022年期间,特斯拉员工通过内部消息系统私下分享了一些车主车载摄像头记录的隐私视频和…...

Doris(2):Doris编译部署
1 Doris编译 Apache Doris提供直接可以部署的版本压缩包:https://cloud.baidu.com/doc/PALO/s/Ikivhcwb5 也可以自行编译压缩包后使用(推荐) 1.1 使用 Docker 开发镜像编译(推荐) 这个是官方文档推荐的,…...
使用MyBatis实现简单查询
文章目录一,创建数据库与表(一)在Navicat里创建MySQL数据库testdb(二)创建用户表 - t_user(三)在用户表里插入3条记录二,案例演示MyBatis基本使用(一)创建Mav…...
[4]和char *point[4])
C指针(*point)[4]和char *point[4]
char (*point)[4] // 数组指针。 a[3][4] // 先申明二维数组,用它来指向这个二维数组. char *point[4] // 指针数组。 a[4][5] // 一连串的指针. char (*point)[4] // 一个指针,指向有4个元素的数组;占内存大小为 4 个字节 ch…...
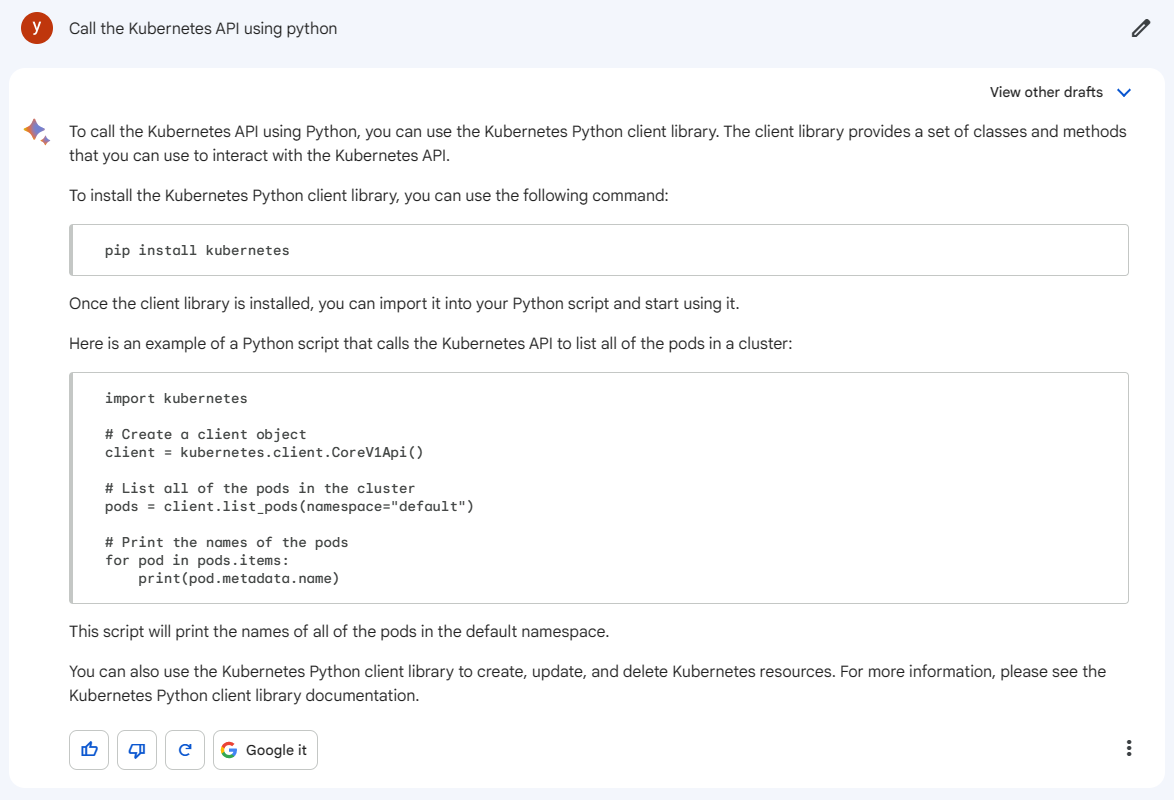
【Bard】谷歌的人工智能工具—Bard初体验
文章目录一、Bard介绍二、Bard体验1、加入Bard的候补名单2、登入Bard篇3、使用Bard篇(1)提供三种预选方式✨(2)创作生成各类文案(3)无生成图画能力(4)支持语音转文本输入✨ÿ…...
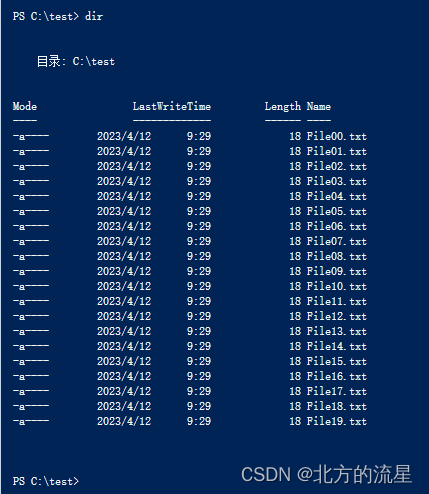
2022国赛30:windows脚本题解析
大赛试题内容: ( 九) ) 脚本 【任务描述】 为了减少重复性任务的工作量,节省人力和时间,请采用脚本,实现快速批量的操作。 1.在 windows4 上编写 C:\CreateFile.ps1 的 powershell 脚本,创建20 个文件 C:\test\File00.txt 至 C:\test\File19.txt,如果文件存在,则首先删除…...
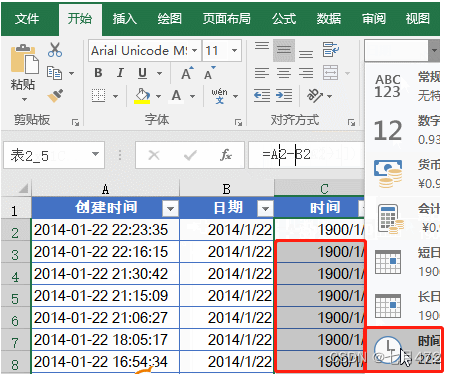
Excel常用函数公式20例
目录 一、【IF函数条件判断】 二、【多条件判断】 三、【条件求和】 四、【多条件求和】 五、【条件计数】 六、【多条件计数】 七、【条件查找】 八、【多条件查找】 九、【计算文本算式】 十、【合并多个单元格内容】 十一、【合并带格式的单元格内容】 十二、…...
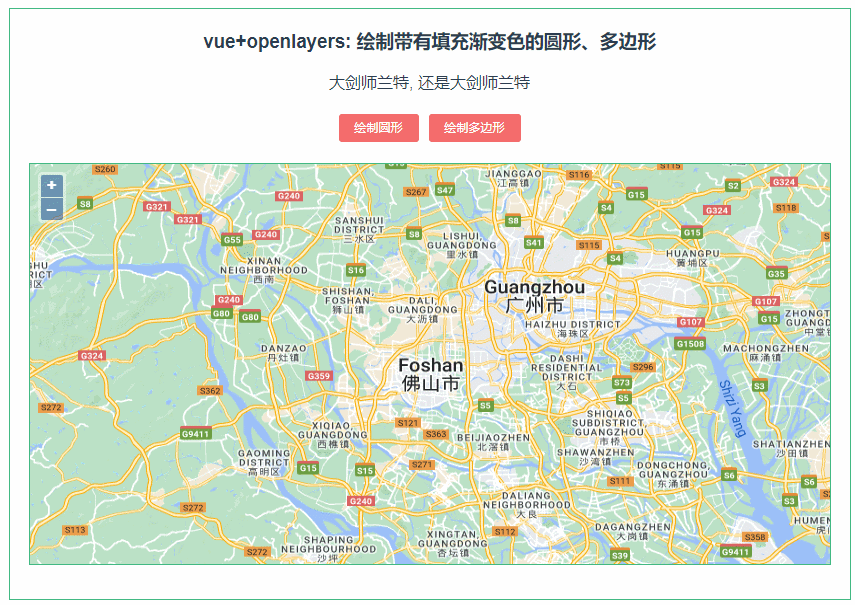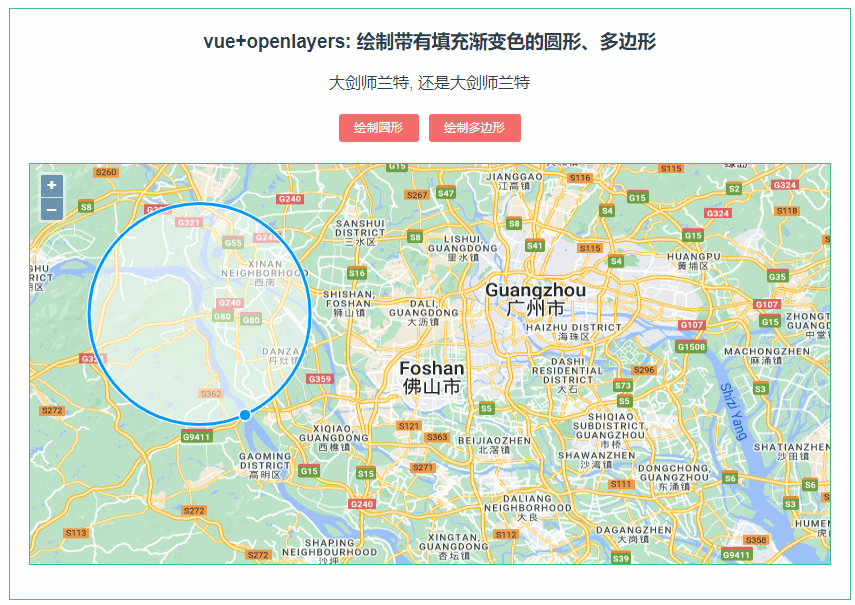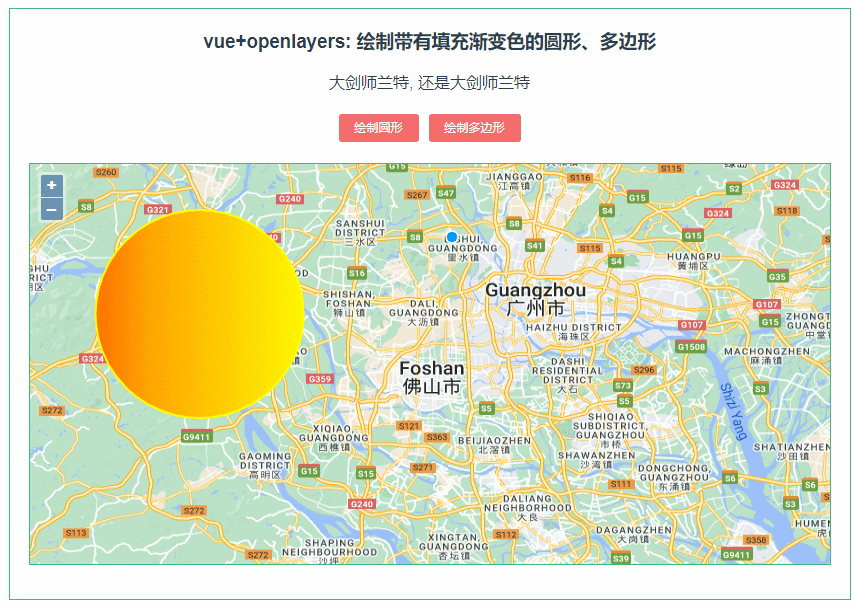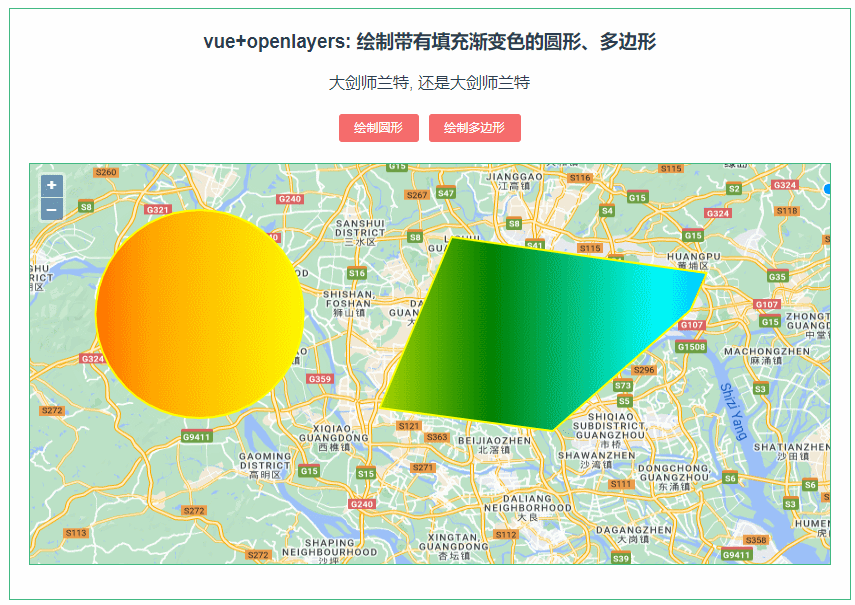
233:vue+openlayers绘制渐变填充色的圆形、多边形
第233个 点击查看专栏目录 本示例的目的是介绍如何在vue+openlayer中绘制带有渐变填充色的圆形、多边形。这里用canvas的方式去渲染,用到了DEVICE_PIXEL_RATIO,设备上的物理像素与设备无关像素 (dips) 之间的比率 (window.devicePixelRatio)。 直接复制下面的 vue+openlayer…...
Flink的窗口机制
窗口机制 tumble(滚动窗口) hop(滑动窗口) session(会话窗口) cumulate(渐进式窗口) Over(聚合窗口) 滚动窗口(tumble) 概念 滚…...

了解分布式Session
大家好,我这名CRUD工程师又来了,最近我的一个同事突然在看分布式Seesion的问题,然后我们两个也是互相讨论了一下,今天我就想着把分布式Session的知识点好好的梳理一下。 在很多系统中,用户的登录功能都是用Session去实…...

仿真创新大赛—国三省一 智能鱼缸(proteus)(stm32)
⏩ 大家好哇!我是小光,嵌入式爱好者,一个想要成为系统架构师的大三学生。 ⏩去年下半年参加了全国仿真创新大赛,也是取得了国赛三等奖,省赛一等奖的好成绩。 ⏩本篇文章对我们的参赛作品《智能鱼缸》做一个简介。 ⏩感…...

【ARMv8 编程】A64 数据处理指令——位域字节操作指令
有些指令将字节、半字或字扩展到寄存器大小,可以是 X 或 W。这些指令存在于有符号(SXTB、SXTH、SXTW)和无符号(UXTB、UXTH)变体中,并且是适当的位域操作指令。 这些指令的有符号和无符号变体都将字节、半字…...

ctfshow 愚人杯菜狗杯部分题目(flasksession伪造ssti)
目录 <1>愚人杯 (1) easy_signin (2) easy_ssti(无过滤ssti) (3) easy_flask(flash-session伪造) (4) easy_php(C:开头序列化数据) <2> 菜狗杯 (1) 抽老婆(flask_session伪造) (2) 一言既出,驷马难追(intval) (3) 传说之下(js控制台&…...

linux拓展笔记——【补充学习知识点】
文章目录1. ./configure --prefix中的prefix详解1. ./configure --prefix中的prefix详解 源码的安装一般由3个步骤组成:配置(configure)、编译(make)、安装(makeinstall)。 Configure是一个可执行脚本,在待安装的源码路径下使用命令./configure–help输…...

为何银行各岗位之间的薪酬差别如此之大?
银行里的职位种类相对较多,观观整理了5个最常见的职位,看一下你要申请的职位薪资水平到底是怎样的?根据如信银行考试中心发布: 1、客户经理岗 客户经理分为对公客户经理和对私客户经理,他们的主要工作不同࿰…...
TensorFlow 深度学习第二版:1~5
原文:Deep Learning with TensorFlow Second Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只…...
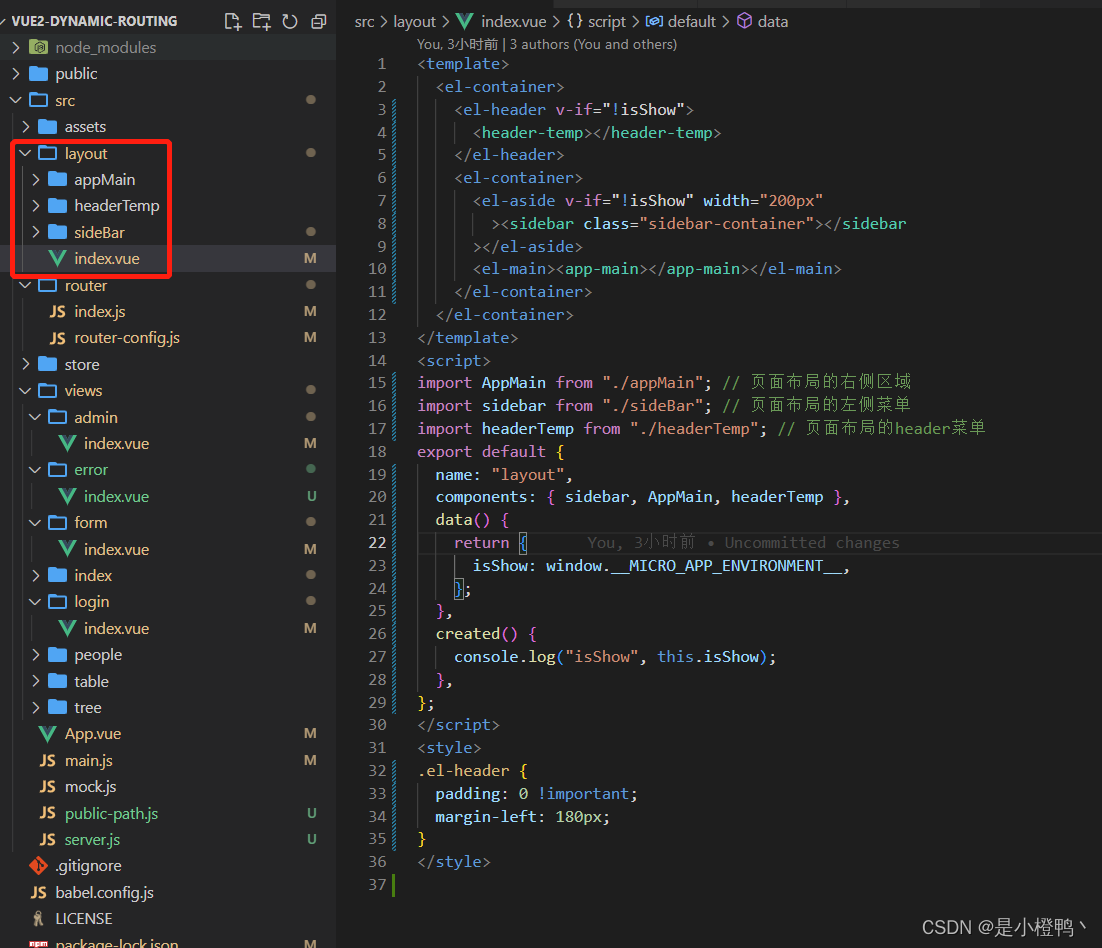
微前端micro-app的使用
演示效果 子应用的项目 基应用嵌入子应用效果图 目录 前言 一、微前端是什么? 它主要解决了两个问题: 二、使用步骤 1.安装依赖 2.在入口处引入 3.子应用的路由() 4.分配一个路由给子应用(重要)࿰…...

【JUC】Java内存模型之JMM
【JUC】Java内存模型之JMM 文章目录【JUC】Java内存模型之JMM1. 概念2. JMM三大特性2.1 可见性2.2 原子性2.3 有序性3. 多线程对变量的读写过程4. 先行发生原则——happens-before4.1 happens-before八条规则4.1.1 次序规则4.1.2 锁定规则4.1.3 volatile变量规则4.1.4 传递规则…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
