开放式耳机新巅峰!南卡OE Pro兼备澎湃音质、舒适佩戴、创新设计
众所周知,当初苹果带来TWS耳机新时代以后,后面有许多的蓝牙耳机相继跟随和模仿,但NANK南卡却独辟蹊径,将在近日重磅推出首款0压·无感·全开放无线耳机——南卡OE Pro,走向开放式TWS耳机的新时代。

31度黄金倾斜受力面,上耳佩戴0压感
相比于传统的蓝牙耳机,开放式耳机在佩戴显得更为突出,不像入耳式压迫耳道,可以更好地守护耳朵健康。佩戴时在耳畔两侧,犹如时尚装饰,显得个人品味蹭蹭上涨,可以轻松驾驭在办公室、运动以及图书馆,开放式的耳挂设计,采用0压无感全开放,安全舒适不全入耳,不给耳朵任何负担,长时间佩戴无忧。

并且耳机本体设计是采用31度黄金倾斜受力面,将耳挂的形态曲线可与耳轮、耳后根的结构自然贴合,贴合耳朵造型,轻松驾驭任何大小耳朵,贴肤部分是采用医疗级液体硅胶材质亲肤顺滑的质感,具有一定的柔韧性,能够自动回弹,佩戴稳固不易掉落。

专业声学技术,定制高通蓝牙5.2芯片,聆听最真实的音质
由于是开放式的耳挂设计, 南卡OE Pro开放式的发声单元更为人性化地固定在两侧耳廓,不会产生压迫耳膜,有效保护耳朵,而且在音质方面是Super Bass 2.0高性能声音单元以及南卡Super sound OS发烧级声学系统,能够智能补偿音质曲线,实现高至98.6%的高保真。

采用高通蓝牙5.2技术,耳机连接很稳定,听音乐、通话均未出现断连或者卡顿等情况,完全不会影响听音乐、追剧等娱乐需求;支持Aptx无损音质传输,并且具有16.2mm大动圈,具有2倍超宽音域,搭配复合钛膜,中高频表现清亮,并且声场广阔,声音的清晰度和层次感震撼人心。

频响范围是传统声音单元2倍,在三频方面的表现都很优秀,尤其是对人声的表现更是可圈可点的,采用突破性的DS指向性传声技术,并通过对多级音腔镂空的精准调校,定位声音的传输方向,有效防止漏音产生的同时,让声音更加集中。
低至60ms的赛事级别延迟,打造沉浸体验
为了满足游戏玩家的需要,南卡OE Pro开放式耳机具有低至60ms的赛事级别延迟,几乎不会有任何声音延迟的问题,均能即时传到耳边,能够很清楚地听到附近声音细节,由于有16.2mm大动圈的加持,使得脚步声更沉重与明显,游戏空间临场感很足,能够更酷爱做出更准确和快速的判断。

并且游戏模式还研发了南卡 Game mode 低延时处理技术,为手游场景提供专属信号通道,屏蔽外界信号干扰,拾音清晰稳定,将战场信息清晰地传递至队友,同时优化信号传输功率,有效降低83%的声音延时,总体来说,游戏耳机并没有明显短板,玩游戏够用了,还能满足日常观影娱乐的聆听需求。
四麦通话降噪,无惧环境干扰
同时,南卡OE Pro开放式耳机采用通话降噪技术,ENC通话降噪技术加上四麦克风,可以做到定向拾音,精准拾音,可以有效滤除环境噪音,让每次通话清晰如面谈,能做到清晰接听,不用担心在环境吵闹的地段通话,无惧无惧环境干扰。

防水续航再升级,畅快运动无阻
对于喜欢佩戴蓝牙耳机的运动人士来说,避免不了运动后产生的汗水,南卡OE Pro开放式耳机具有IPX5的防水等级,满足日常运动、生活佩戴所需,再也不用担心跑步出汗、淋雨等侵袭,但切记不能浸泡在水中。

出色的续航表现。而综合续航可达25小时,一周最多给充电盒充一次电,完全可以接受,再加上C口和快速充电技术的加持,为充电盒充电带来了便利,更何况还支持无线充电,不仅进一步提升产品寿命,日常使用也更为方便。

总体而言,在千篇一律的真无线耳机市场里,从外观设计,到耳道清爽的开放佩戴,还有出色音质,以及超低延迟的操作,这些都是南卡OE Pro开放式真无线耳机的加分项,在我看来,这副开放式耳机是领域的一个设计标杆。如果你对耳机佩戴舒适度有较高要求,相信会给你超预期的体验。
相关文章:

开放式耳机新巅峰!南卡OE Pro兼备澎湃音质、舒适佩戴、创新设计
众所周知,当初苹果带来TWS耳机新时代以后,后面有许多的蓝牙耳机相继跟随和模仿,但NANK南卡却独辟蹊径,将在近日重磅推出首款0压无感全开放无线耳机——南卡OE Pro,走向开放式TWS耳机的新时代。 31度黄金倾斜受力面&…...
1700页,卷S人的 Java《八股文》PDF手册,涨薪跳槽拿高薪就靠它了
大家好,最近有不少小伙伴在后台留言,又得准备面试了,不知道从何下手! 不论是跳槽涨薪,还是学习提升!先给自己定一个小目标,然后再朝着目标去努力就完事儿了! 为了帮大家节约时间&a…...

普通人是否能从ChatGPT中分一杯羹?
ChatGPT3.0刚刚推出,最开始的时候,人们只是将ChatGPT看作一个很会聊天的机器人,无论问题多么天马行空,它的答案看上去都有理有据。后来,像打开潘多拉魔盒一样,很多人开始拿它编大纲、撰写文案、编代码、创作…...
SpringBoot自动装配原理(附面试快速答法)
文章目录SpringBoot自动装配原理1. 从调用SpringApplication构造器方法开始2. 解析启动类4.按需装配4.1 分析dubbo自动装配5. 如果定义自己的starter6. 面试答法SpringBoot自动装配原理 之前面试被问到这个题目,只会答一些spi、AutoConfigration注解、Import之类的&…...
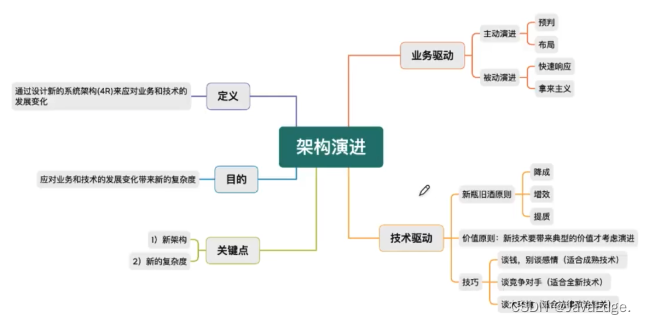
如何在大厂做好架构演进?
1 架构演进的定义 1.1 定义 通过设计新的系统架构(4R),来应对业务和技术的发展变化。 1.2 关键点 新架构新的复杂度 1.3 目的 应对业务和技术的发展变化后带来新的复杂度。 案例 淘宝去IOE,是因为业务发展大了后,IOE的成本和可控性难…...

减半技术实现求a的n次幂
目录 减半技术实现求a的n次幂 程序设计 程序分析 减半技术实现求a的n次幂 【问题描述】给定两个正整数a和n,采用减半技术求a的n次幂;其中a<100,b<20; 【输入形式】两个整数a,n(a与n中间用空格隔开); 【输出形式】一个整数 【样例输入1】2 3 【样例输出1】8 【样…...
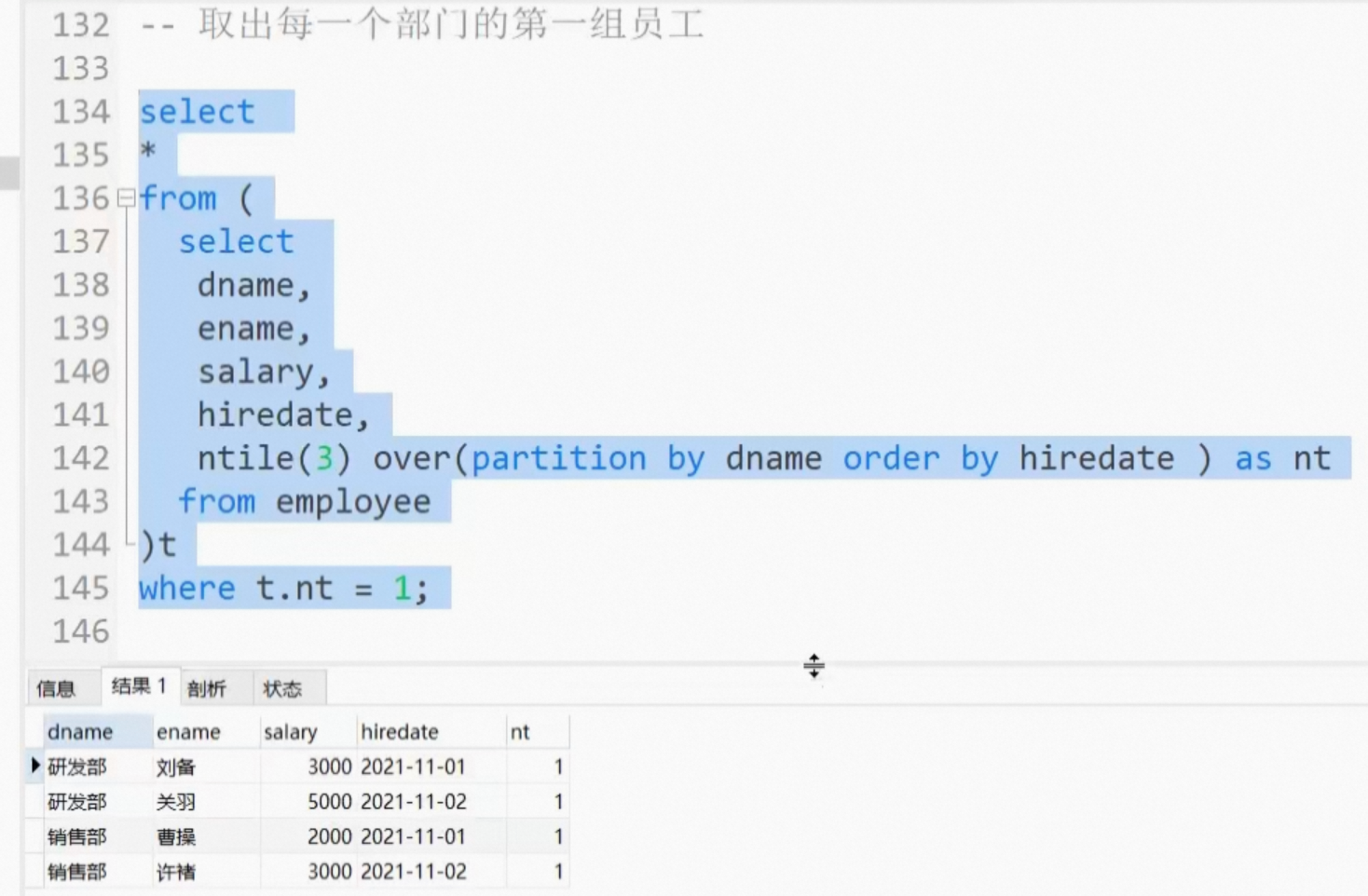
MYSQL8窗口函数
MYSQL8窗口函数 MYSQL8窗口函数窗口函数分类序号函数--排行榜row_number()示例rank()示例dense_rank()示例partition by对每个分区内的行进行排名不加partition by全局排序 开窗聚合函数分布函数CUME_DIST()PERCENT_RANK() 前后函数LAG()的用法LEAD() 头尾函数其他函数NTH_VALU…...
全国大学生智能汽车竞赛——安装Ubuntu操作系统(双系统)
1.1 电脑分区 1.1.1 分区原因 由于我们想要在电脑上同时安装Windows和Ubuntu系统,所以就要在window使用的内存中划分出来一段用来给Ubuntu系统使用,相当于一个应用程序一样 1.1.2 分区步骤 1.右击此电脑,点击管理,然后双击左侧…...
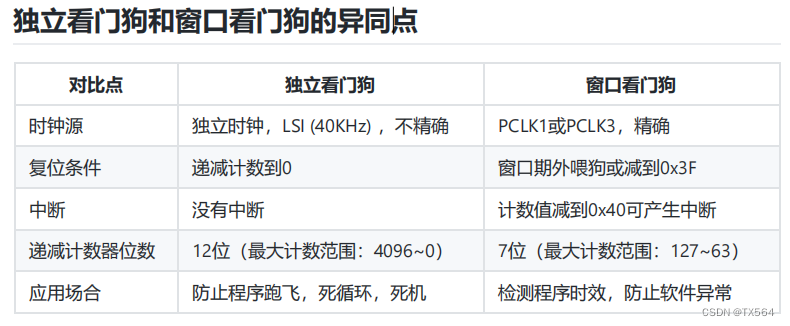
[STM32F103C8T6]看门狗
看门狗: 在由单片机构成的微型计算机系统中,由于单片机的工作常常会受到来自外界电磁场的干扰,造 成程序的跑飞,而陷入死循环,程序的正常运行被打断,由单片机控制的系统无法继续工作,会 造成整个…...

浪潮:2022年净利同比增长51.39%
一、4月头条 华为的紧急回应,让东方材料21亿收购要黄? 4月10日消息,东方材料昨日晚间公告拟定增募资不超20亿元,用于向诺基亚全资子公司NSN收购TD TECH 51%股权(交易对价21.22亿元)。TD TECH剩余49%股权由…...

大厂面试内幕:阿里内部整理出的5000页Java面试复盘指南,起飞!!!
互联网的技术岗一直是高薪的代名词,特别是大厂,应届生的年薪基本都20W起,比一般的公司高多了。 看下面这张网上热传的大厂应届生薪酬表就知道了,SP offer甚至能拿到30W以上。 技术社区也有晒出高薪offer的同学: 除了薪…...

数据结构——哈希表相关题目
数据结构——哈希表相关题目 242. 有效的字母异位词1.暴力解法2.排序后比较3.哈希表 383. 赎金信哈希解法 49. 字母异位词分组438. 找到字符串中所有字母异位词3. 无重复字符的最长子串76. 最小覆盖子串349. 两个数组的交集1.排序双指针2.哈希表 350. 两个数组的交集 II1.排序双…...
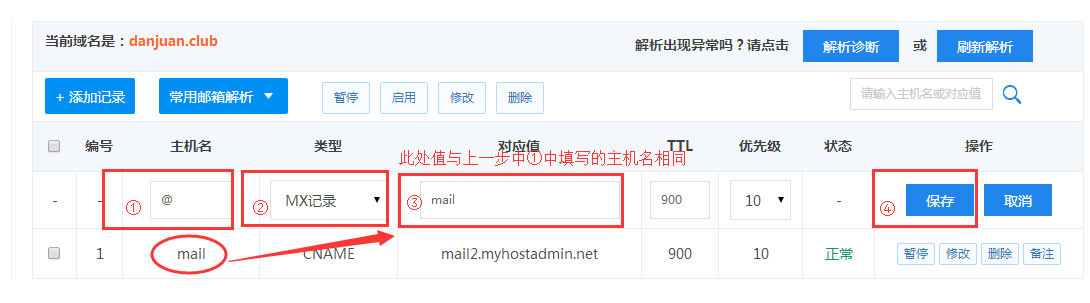
域名解析设置方法
域名解析设置都是实时生效的,一般只需几秒即可同步到各地 DNS 上,但各地 DNS 均有缓存机制,解析的最终生效取决于各运营商刷新时间! 一、A记录 ①.主机名必须填写; 常用主机名有:www//*,效果参见上图说明&…...

MySQL连接空闲时间超过8小时报错原因与延伸知识
1 错误原因 1.1 两个参数 MySQL服务端两个参数控制连接超时时间: wait_timeoutinteractive_timeout1.1.1 如何查看 show global variables like interactive_timeout show global variables like wait_timeout 复制代码 1.1.2 含义与区别 wait_timeout…...
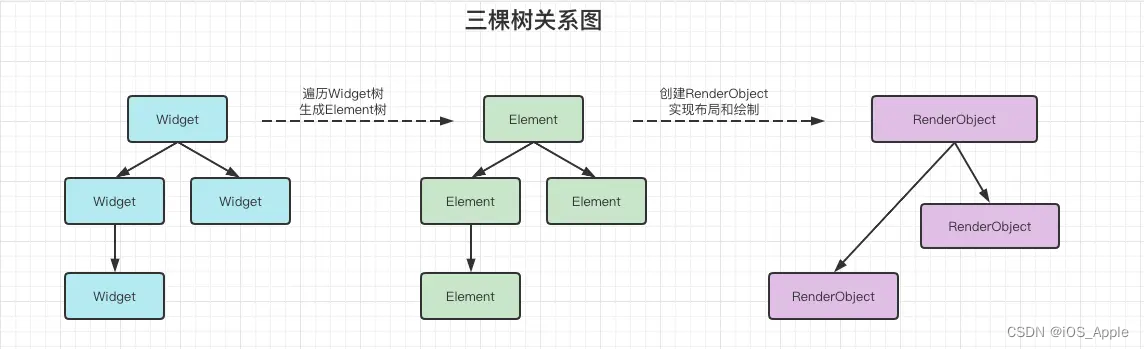
Flutter渲染原理
一 Widget Element RenderObject 之间的关系 1 Widget 在Flutter 中,万物皆是Widget,无论是可见的还是功能型的。一切都是Widget. 官方文档中说的Widget 使用配置和状态来描述View 界面应该长什么样子。 它不仅可以表示UI元素,也可以表示一些功能性的…...
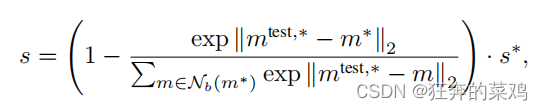
PathCore:IAD文献解读
论文链接:[Towards Total Recall in Industrial Anomaly Detection]Towards Total Recall in Industrial Anomaly Detection :数据集, :标签 : 在ImageNet上预训练后的网络 第 张图 网络中第 层 1. Locall…...

C语言判断一个日期是在该年的第几天案例讲解
今天是2023年4月11号,我们就用今天举例得出是2023年的第几天。 思路分析 1)我们想知道2023年4月11号是2023年的第几天,只需要把1到3月份的天数累加求和然后加上今天日期也就是11就可以算出2023年4月11号是2023年的第几天。 推广:…...

【超全总结】集成环信消息推送注意事项(华为、oppo、vivo等)
环信即时通讯 IM 支持集成第三方厂商的消息推送服务,为 Android 开发者提供低延时、高送达、高并发、不侵犯用户个人数据的离线消息推送服务。 当客户端应用进程被关闭等原因导致用户离线,环信即时通讯 IM 服务会通过第三方厂商的消息推送服务向该离线用…...

C++回调函数以及epoll中回调函数的使用
回调函数是一种常用的编程技术,它允许程序在运行时将一个函数作为参数传递给另一个函数,以实现更加灵活和可扩展的功能。在C中,回调函数通常被实现为函数指针或者函数对象。 函数指针是指向函数的指针变量,可以通过它来调用函数。…...
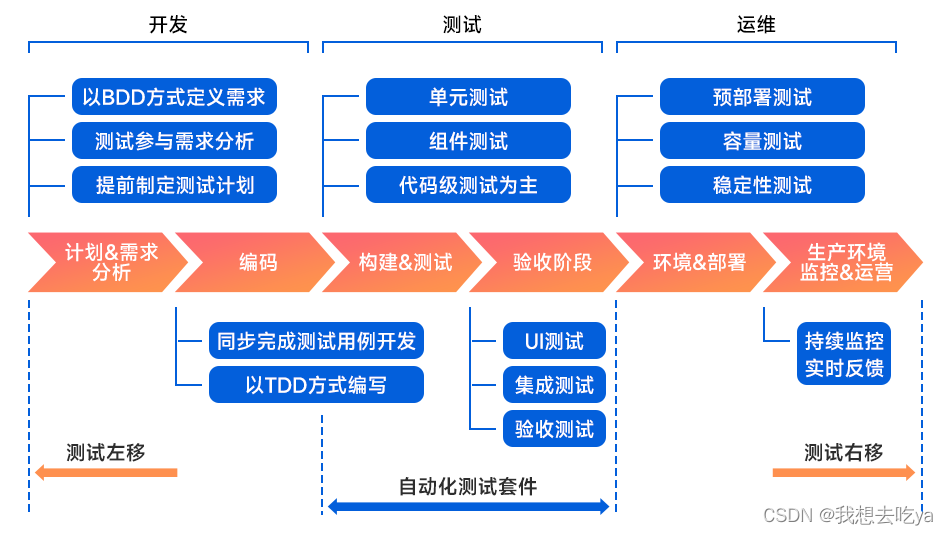
0基础学习软件测试有哪些建议
其实现在基础的资料和视频到处都是,就是看你有没有认真的去找学习资源了,去哪里学习都是要看你个人靠谱不靠谱,再好的教程和老师,你自己学习不进去也是白搭在正式选择之前,大可以在各种学习网站里面找找学习资源先自己…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
