二叉树基础概念
1.二叉树种类
1.1 满二叉树
满二叉树:如果一棵二叉树只有度为 0 0 0 的结点和度为 2 2 2 的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
如图所示:
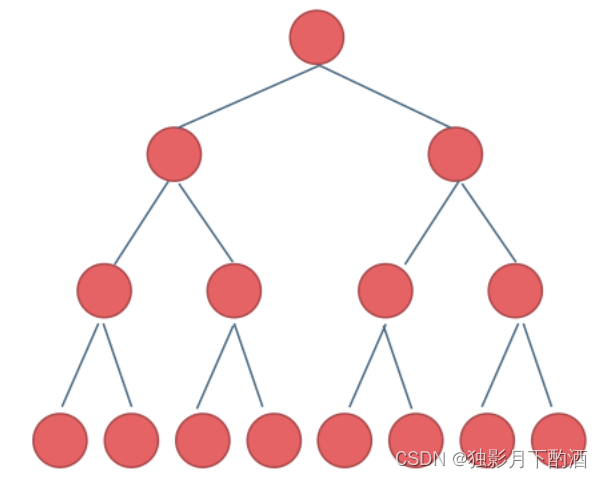
这棵二叉树为满二叉树,也可以说深度为 k k k,有 2 k − 1 2^k-1 2k−1 个节点的二叉树。
图中二叉树的深度为4,叶子节点个数= 2 4 − 1 = 15 2^4-1=15 24−1=15
1.2 完全二叉树
什么是完全二叉树?
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h h h 层,则该层包含 1 1 1~ 2 ( h − 1 ) 2^{(h-1)} 2(h−1) 个节点。
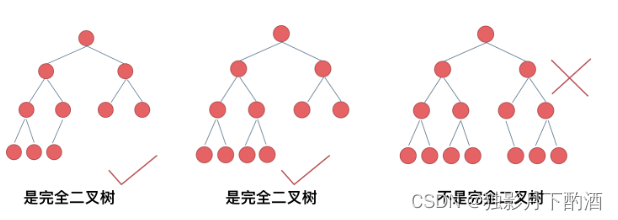
优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
1.3 二叉搜索树
二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树:
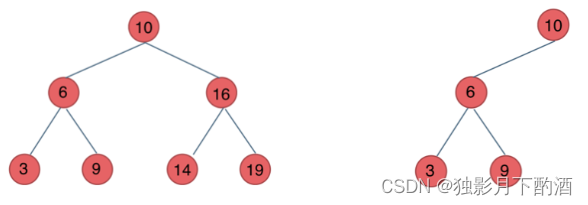
1.4 平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
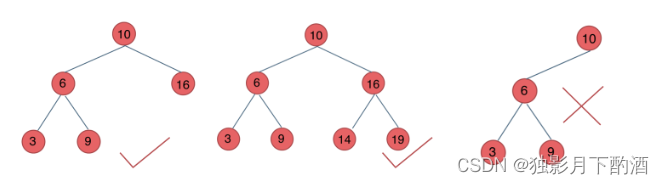
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了 1 1 1。
2.二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。
链式存储如图:
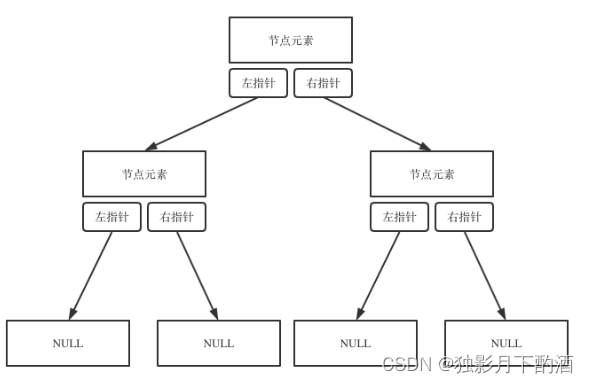
顺序存储的方式如图:
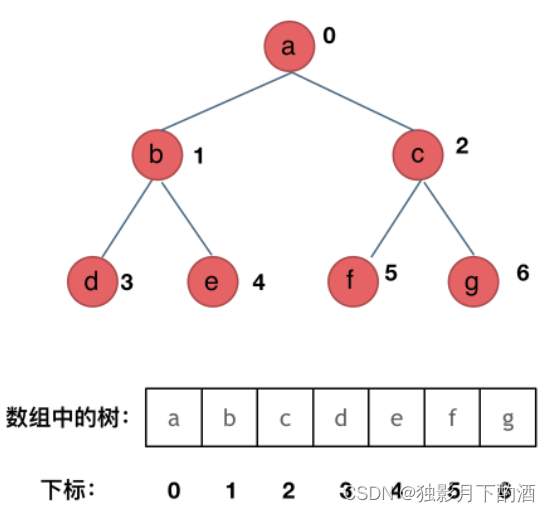
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i i i,那么它的左孩子就是 i ∗ 2 + 1 i * 2 + 1 i∗2+1 ,右孩子就是 i ∗ 2 + 2 i * 2 + 2 i∗2+2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
所以大家要了解,用数组依然可以表示二叉树。
3.二叉树的遍历方式
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
这里前中后,其实指的就是中间节点的遍历顺序
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中

二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种是实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
4.二叉树的定义
class TreeNode: def __init__(self, value):self.value = valueself.left = Noneself.right = None
相关文章:

二叉树基础概念
1.二叉树种类 1.1 满二叉树 满二叉树:如果一棵二叉树只有度为 0 0 0 的结点和度为 2 2 2 的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。 如图所示: 这棵二叉树为满二叉树,也可以说深度为 k k k&…...

【MySQL】(1)数据库基础,库与表的增删查改,数据库的备份与还原
文章目录服务器,数据库,表关系MySQL 数据存储逻辑SQL 分类存储引擎库的操作查看数据库创建数据库查看创建语句删除数据库选择(切换)数据库查看当前选择的数据库修改数据库字符集和排序规则表的操作创建表查询表查询表结构插入数据…...

Python基础-01 变量
注释 注释的分类 在Python中,支持单行及多行注释 单行注释 使用#对代码进行说明,#右边的所有内容就是注释的内容,起辅助说明作用 # #右边的都是注释,解析器会忽略 print(hello world) #在控制台里打印一段话多行注释 多行注释中,允许换行,使用三个单引号开始,三个单引号结…...
springcloud2.1.0整合seata1.5.2+nacos2.10(附源码)
springcloud2.1.0整合seata1.5.2nacos2.10(附源码) 1.创建springboot2.2.2springcloud2.1.0的maven父子工程如下,不过多描述: 搭建过程中也出现很多问题,主要包括: 1.seataServer.properties配置文件的组…...

map原理
map源码结构体: type hmap struct {count int // 元素的个数B uint8 // buckets 数组的长度就是 2^B 个overflow uint16 // 溢出桶的数量buckets unsafe.Pointer // 2^B个桶对应的数组指针oldbuckets unsafe.Pointer // 发生扩容时࿰…...
概览)
[Ext JS]3.6 Ext JS 表格(Grid)概览
Grid, 翻译过来是网格, 也就是表格。 Grid 的基本构成 面板 :Ext.grid.Panel表格视图 :Ext.view.Table。 不直接使用, 通过面板的viewConfig配置项进行配置。比如可以用来配置表格中行是否跳色显示列: Ext.grid.column.Column。 表格中的列定义store , 表格的数据示例代码…...
关于使用云渲染的五大优势
在不影响质量或性能的情况下节省时间、金钱和资源,对于需要在通常较短且严格的期限内创建高质量 3D 内容的专业人士来说,云渲染都是最好的选择!云渲染作为数字媒体生产的最新趋势,与传统的渲染农场和机器相比具有许多优势…...

CSS基础样式
1.高度和宽度 .c1{height:300px;width:500px; } 注意事项: 宽度,支持百分比 行内标签:默认无效 块级标签:默认有效(右侧区域就算是空白,也不给占用) 2.块级和行内标签 css样式:标签…...

第03章_流程控制语句
第03章_流程控制语句 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 流程控制语句是用来控制程序中各语句执行顺序的语句,可以把语句组合成能完成一定功能的小逻辑模…...
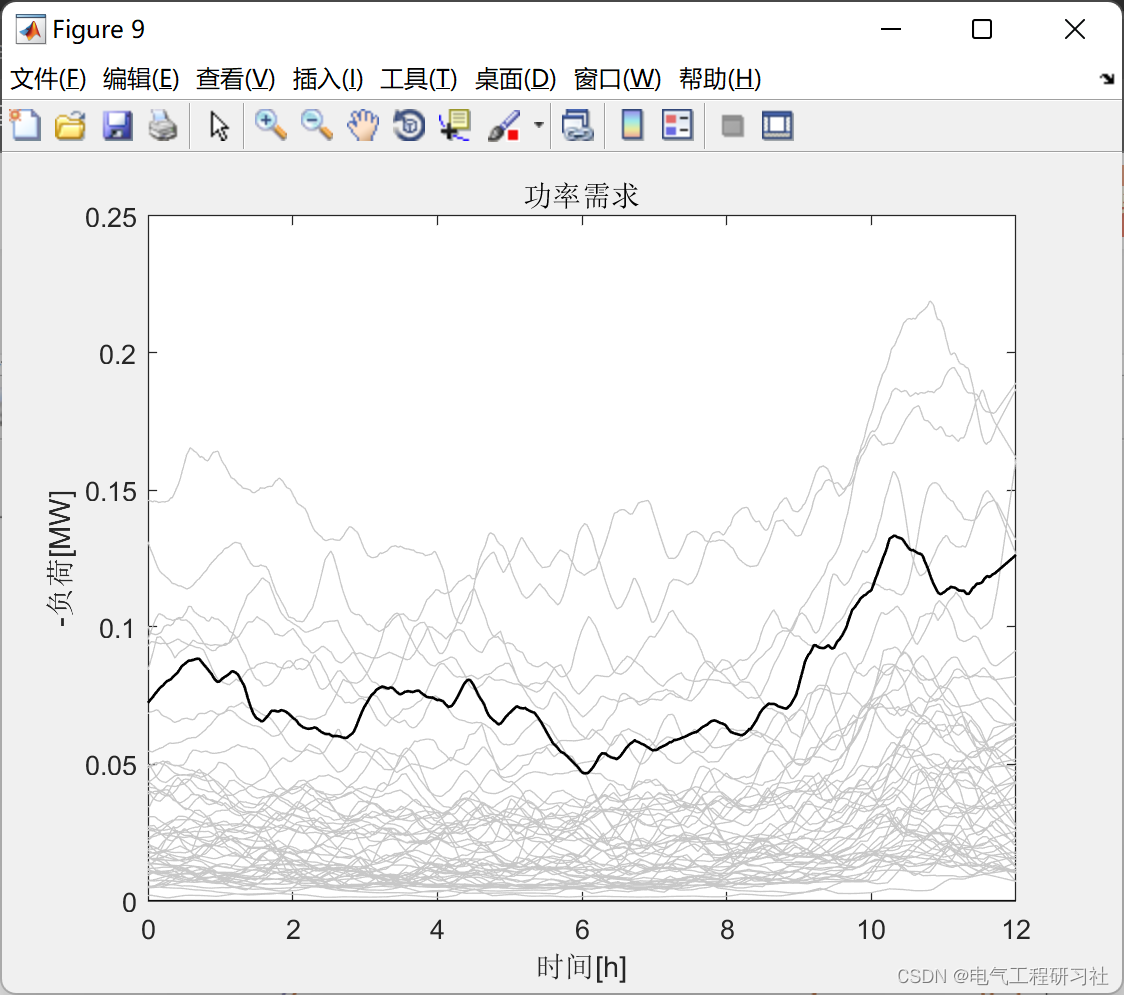
配电网电压调节及通信联系研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

stegano(图片隐写、摩斯密码)
附件是PDF,我们在选择内容时发现光标溢出了文本 说明这里还存在一些我们看不到的内容 直接CtrlA全选,CtrlC复制后新建一个纯文本文件 将复制的东西粘贴过去 粘贴后发现果然多出来了一些东西,提取出来 BABA BBB BA BBA ABA AB B AAB ABAA A…...
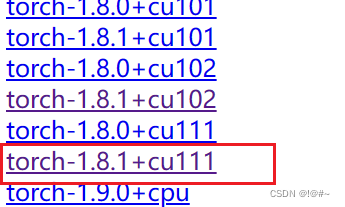
wsl安装torch_geometric
在官网选择需要的版本 选择安装途径,选择runfile 执行第一行,会下载一个文件到目录下 需要降低C的版本,否则 执行sudo sh cuda_11.1.0_455.23.05_linux.run,会出现 查看对应的文件,会有 可以加上override参数之后,…...
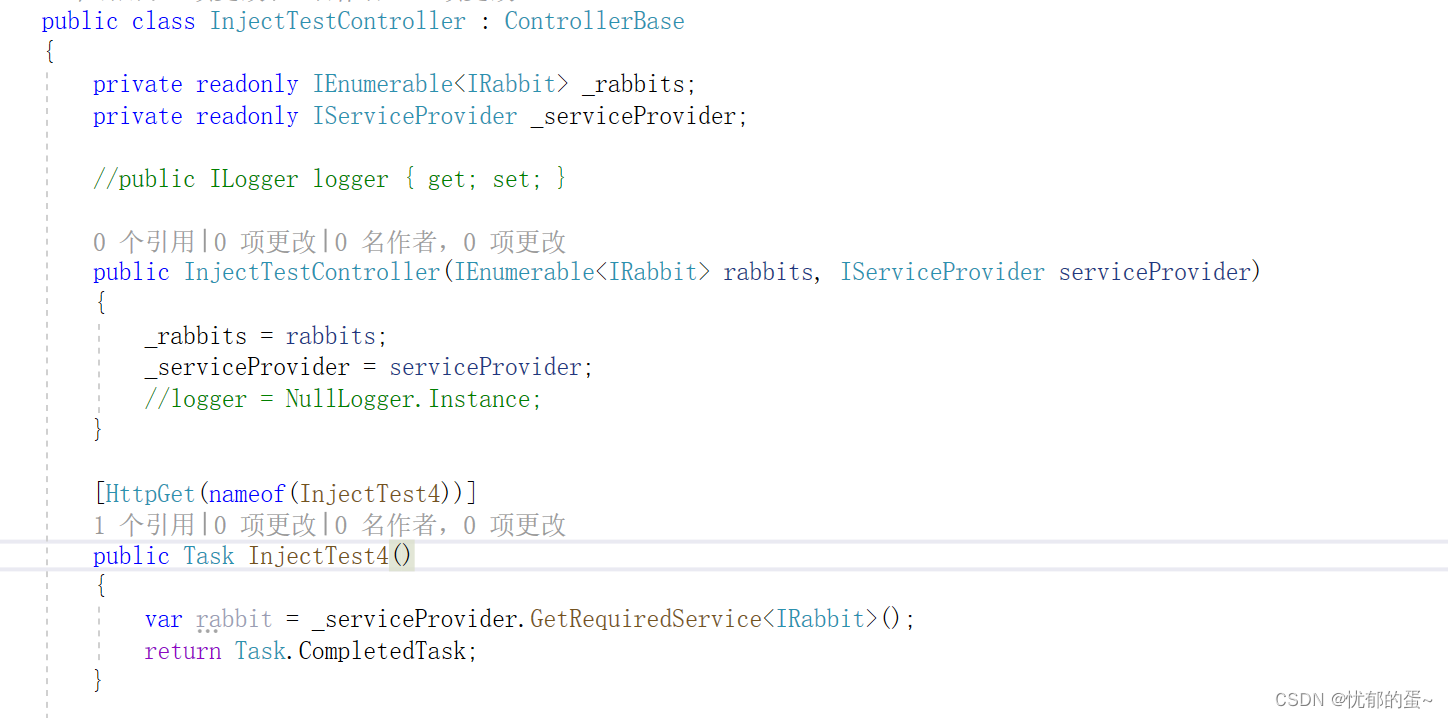
ASP.NET Core - 依赖注入(二)
2,NET Core 依赖注入的基本用法 话接上篇,这一章介绍 .NET Core 框架自带的轻量级 Ioc 容器下服务使用的一些知识点,大家可以先看看上一篇文章 [ASP.NET Core - 依赖注入(一)] 2.3 服务解析 通过 IServiceCollection 注册了服务之后…...

Scala之集合(1)
目录 集合介绍: 不可变集合继承图:编辑 可变集合继承图 数组: 不可变数组: 样例代码: 遍历集合的方法: 1.for循环 2.迭代器 3.转换成List列表: 4.使用foreach()函数&a…...

公网使用SSH远程登录macOS服务器【内网穿透】
文章目录前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址5. 使用固定TCP端口地址ssh远程前言…...
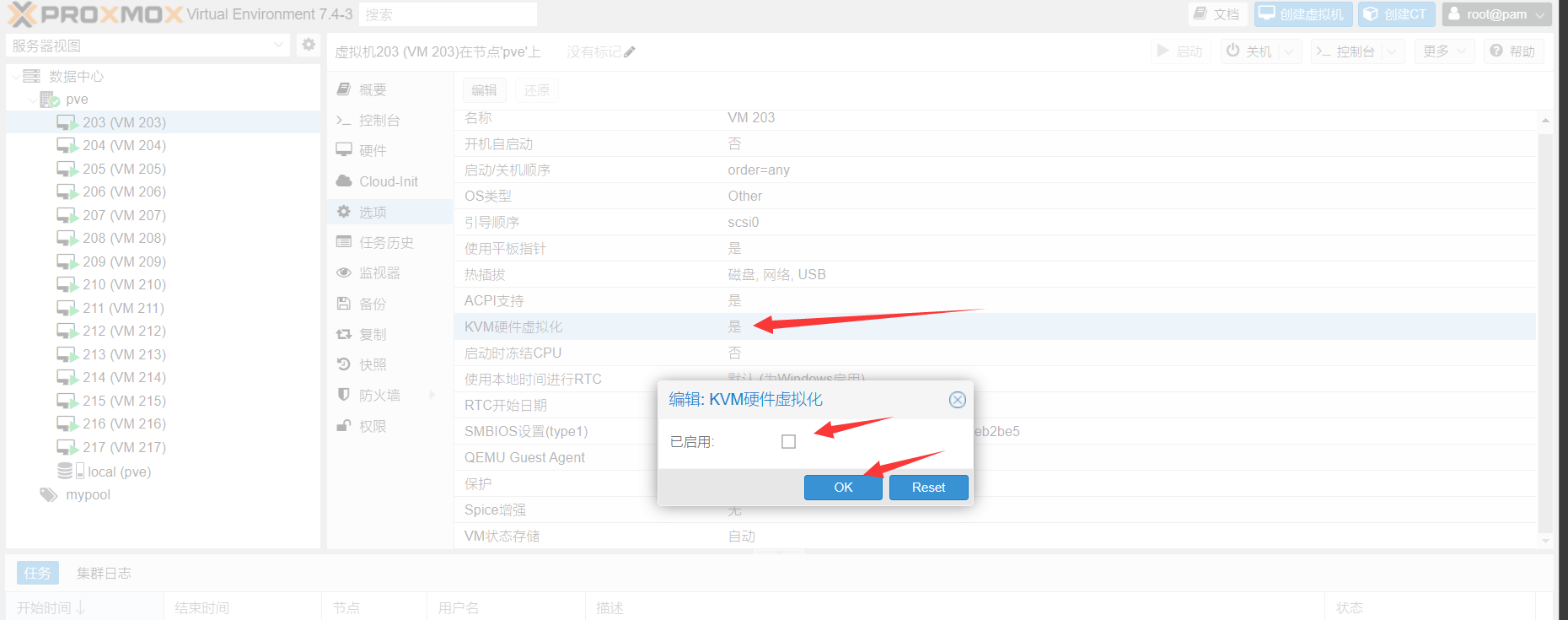
PVE相关的各种一键脚本(一键安装PVE)(一键开设KVM虚拟化的NAT服务器-自带内外网端口转发)
PVE 原始仓库:https://github.com/spiritLHLS/pve 前言 建议debian在使用前尽量使用最新的系统 非debian11可使用 debian一键升级 来升级系统 当然不使用最新的debian系统也没问题,只不过得不到官方支持 请确保使用前机器可以重装系统,…...
)
CSDN目录博客(zhaoshuangjian)
总目录 一、Java1.1 高并发1.2 多线程1.3 集合1.4 I/O1.5 异常1.6 事务1.7 锁机制1.8 JVM 二、数据库2.1 mysql2.1.1 mysql索引2.1.1 mysql锁2.1.1 mysql事务2.1.1 2.2 oracle2.3 postgresql2.4 达梦2.5 人大金仓kingbase 三、设计模式四、中间件4.1 缓存中间件-redis4.2 缓存中…...
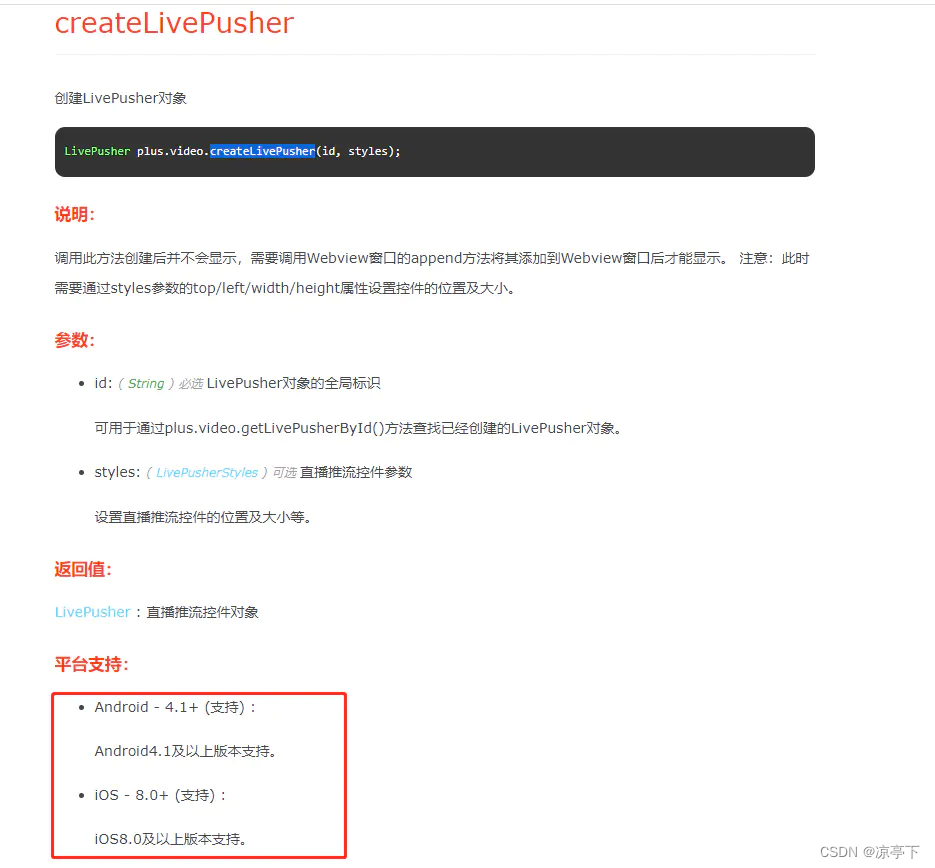
uniapp人脸识别解决方案
APP端: 因为APP端无法使用uni的camera组件,最开始考虑使用内嵌webview的方式,通过原生dom调用video渲染画面然后通过canvas截图。但是此方案兼容性在ios几乎为0,如果app只考虑安卓端的话可以采用此方案。后面又想用live-pusher组件…...

hashlib模块
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起探讨和分享Linux C/C/Python/Shell编程、机器人技术、机器学习、机器视觉、嵌入式AI相关领域的知识和技术。 hashlib模块专栏:《python从入门到实战》 哈希算法,也叫摘要算法。 加密&…...
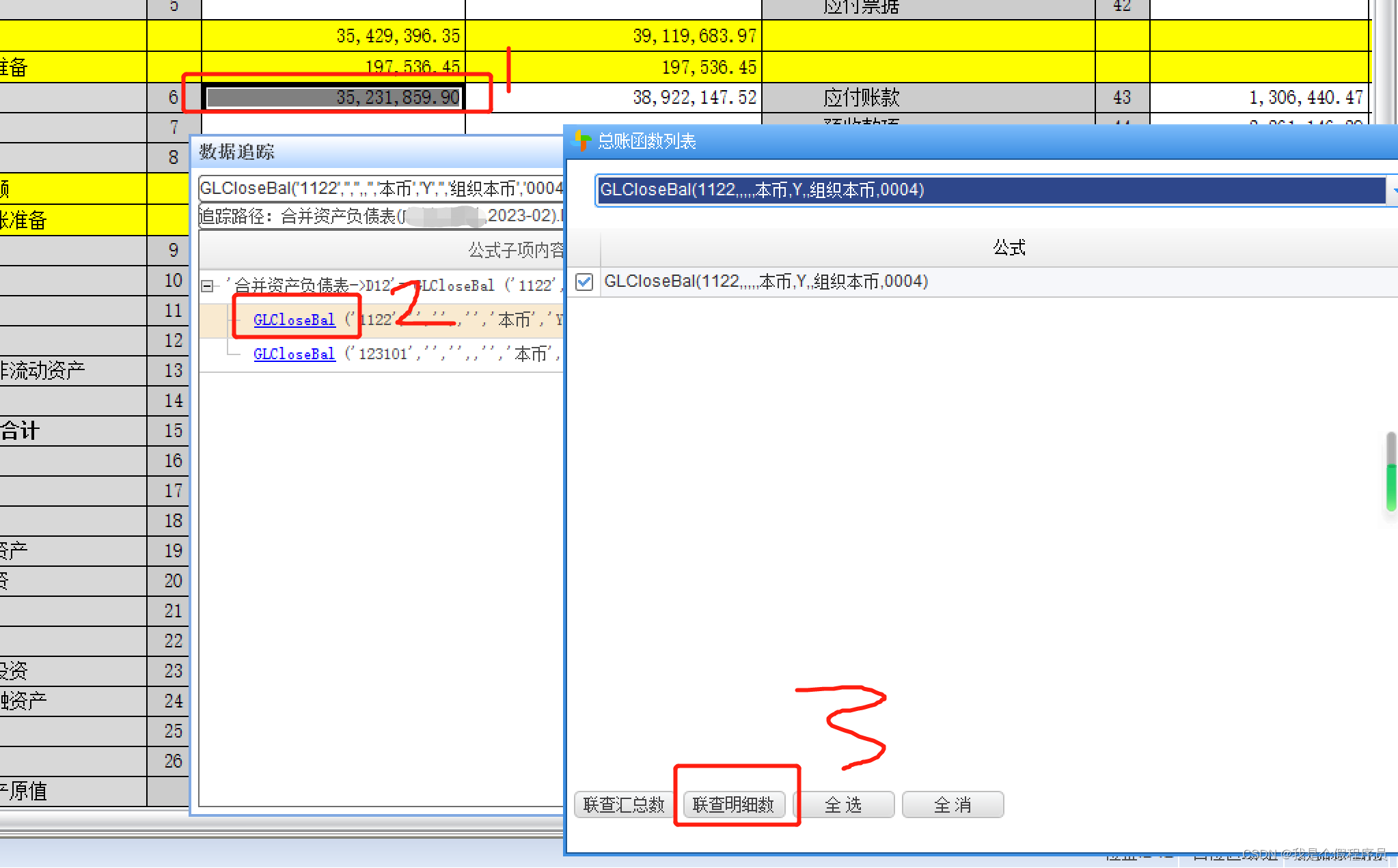
NC65合并报表如何取消上报并退回以及注意事项和相关问题总结
NC65合并报表如何取消上报并退回? 在【企业绩效管理】-【合并报表】-【合并】-【合并执行】节点中,点击〖数据中心〗按钮,在弹出的〖合并报表数据中心〗界面中,点击〖报送管理〗-〖合并方案请求退回〗,然后到【合并综…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
