Scala之集合(1)

目录
集合介绍:
不可变集合继承图:编辑
可变集合继承图
数组:
不可变数组:
样例代码:
遍历集合的方法:
1.for循环
2.迭代器
3.转换成List列表:
4.使用foreach()函数:
可变数组:
ArrayBuffer:
二维数组:
List集合:
Set 集合:
不可变 Set:
可变Set:
Map集合:
创建map:
map集合的遍历:
可变map:
元组:
tuple的定义:
元组与map的关系:
特点:
集合介绍:
不可变集合:
不可变集合继承图: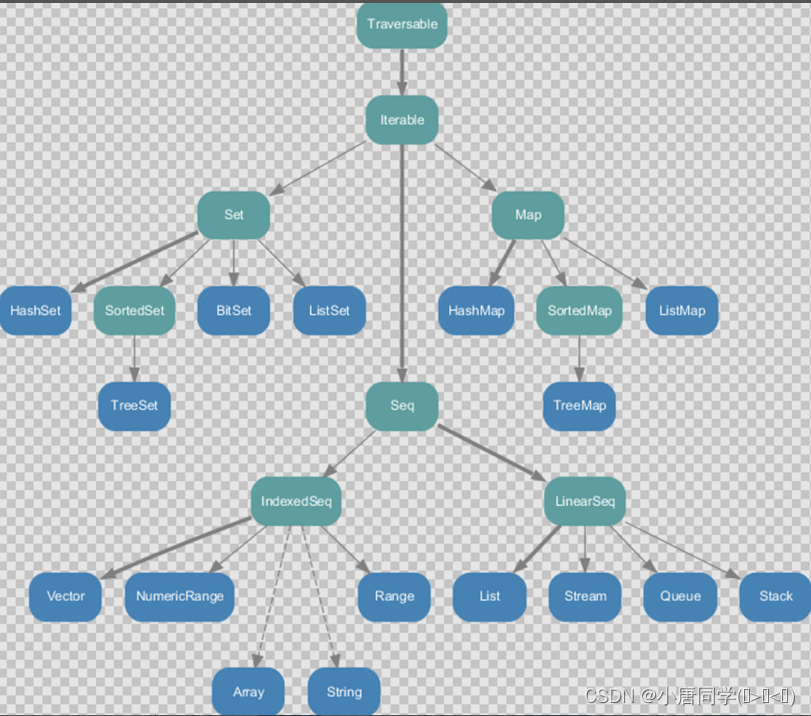
set集合特点:无序,不重复
对set集合无序的理解:set集合的无序是指在使用append等方法给集合添加元素的时候所添加的元素的顺序是不可预测的,并且不能按照添加顺序进行遍历(存储位置是不一定的)
Set集合的无序性是由它的实现方式所决定的。通常,Set集合的实现方式采用了哈希表这种数据结构,其中元素被散列到桶中,不同的元素可能被散列到同一个桶中,因此添加的顺序不能保证元素的顺序。
set集合提供了SortedSet集合是有序的(放入2,3,1,4会按照1,2,3,4进行存储)SortedSet写了一个TreeSet集合是树状存储
可变集合继承图
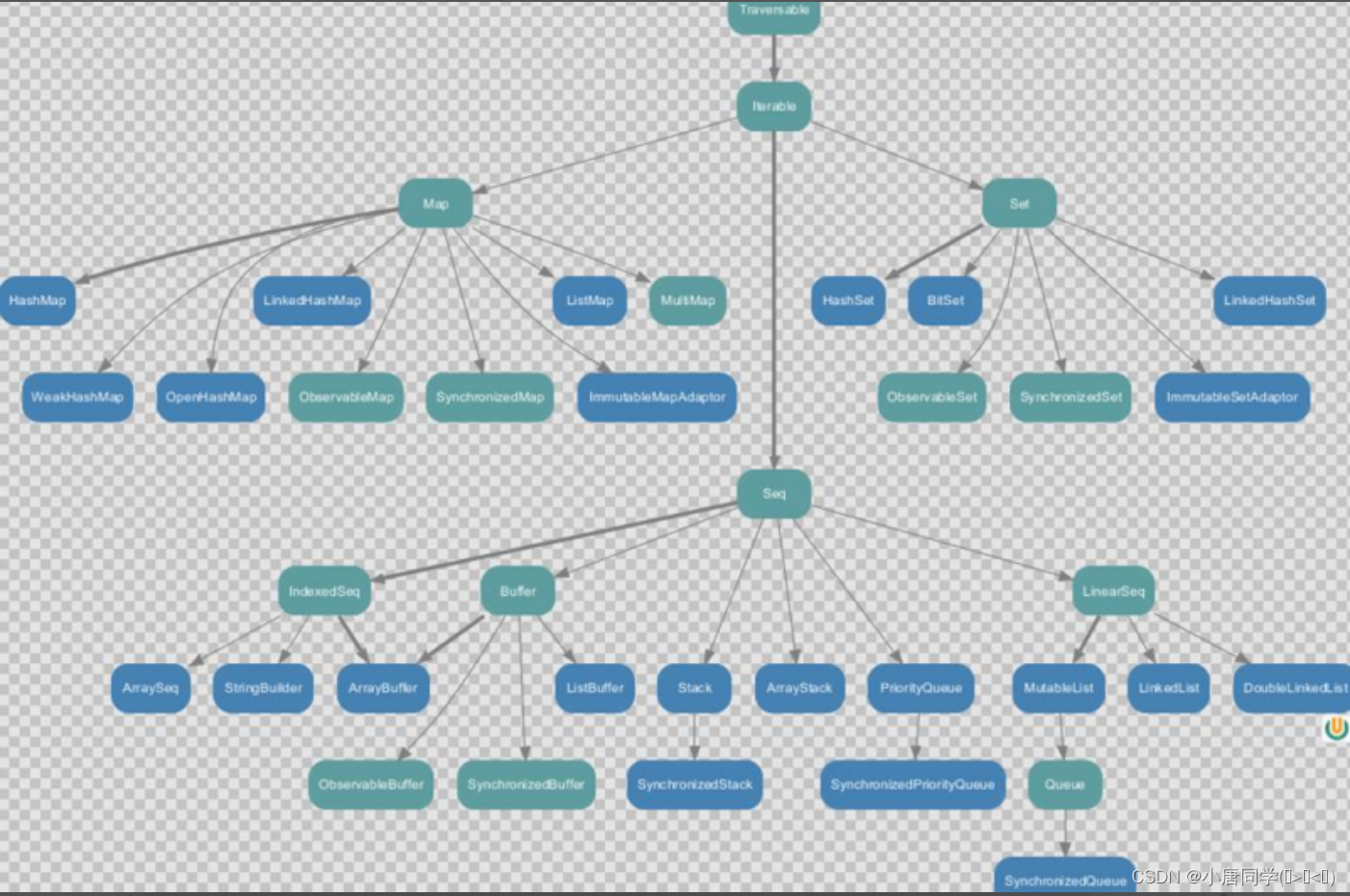
数组:
不可变数组:
不可变集合是长度不可变
Scala中的array 是与 Java中的[]对应
样例代码:
package chapter05
object Test01_Array {def main(args: Array[String]): Unit = {val array = new Array[Int](4)array(3)=100//遍历for (elem <- array) {println(elem)}}
}在Scala中没有写方法名的都是调用了apply方法
遍历集合的方法:
1.for循环
上边样例代码已经使用
2.迭代器
迭代器相当于是指针的跳转(指针在内存中的跳转)
样例代码:
package chapter05
object Test01_Array {def main(args: Array[String]): Unit = {val array = new Array[Int](4)array(3)=100
val iterator: Iterator[Int] = array.iteratorwhile (iterator.hasNext){val i: Int = iterator.next()println(i)}}
}3.转换成List列表:
array集合可以通过to方法转换成List列表
4.使用foreach()函数:
在Scala中给所有的集合都提供了一个foreach()方法 进行函数式打印
foreach()源码:
def foreach[U](f: A => U): Unit = {var i = 0val len = lengthwhile (i < len) { f(this(i)); i += 1 }}源码分析:
foreach()传入的参数实际是传入的函数
A:是代表你传入集合的类型
U:是泛型,代表你的输出类型
这个函数的返回值是Unit类型
让后通过while进行向下运行
对foreach()函数的调用使用匿名函数进行调用
array.foreach(i=>println(i*2))
可变数组:
数组是默认的不可变的,如果需要可变是需要自己导包的
ArrayBuffer:
填入的初始化大小(数组的大小) 只决定了创建底层结构的长度(不填的话默认是16)
ArrayBuffer是可以进行添加元素的append()
可以进行增删改查
可变数组与不可变数组元素的增加区别:
可变的用方法不可变的用符号
代码样例:
可变数组的增删改查:
package chapter05
import scala.collection.mutable.ArrayBuffer
object Test_02_ArrayBuffer {def main(args: Array[String]): Unit = {//可变---导包val arrayBuffer = new ArrayBuffer[Int](4)arrayBuffer.append(1,2,3)arrayBuffer.remove(1)arrayBuffer.update(0,100)println(arrayBuffer(0))println(arrayBuffer)}
}
不可变数组是不可变的,如果使用符号做出改变会生成一个新的对象
val array = new Array[Int](10)val array1: Array[Int]= array :+ 8println(array1.toList)使用to方法可以让可变与不可变数组进行相互转换
二维数组:
二维数组的定义与遍历:
val array2: Array[ Array[Int]] = Array(Array(1, 2, 3),Array(1, 2, 3),Array(1, 2, 3))for (array3 <- array2) {for (elem <- array3) {print(elem+ "\t")}println()}在Scala中创建多维数组的方法:
val array3: Array[Array[Int]] = Array.ofDim[Int](3, 4)
List集合:
List是一个抽象类 在不继承的情况下是无法new的,所以需要使用伴生对象的apply方法
直接使用即可
val list = List(1, 2, 3, 4)
list.foreach(println)
val ints: List[Int] = list :+ 10ints.foreach(println) val list1: List[Int] = 10 :: listlist1.foreach(println) val list2 = List(5, 6, 7, 8)val ints1: List[Int] = list ::: list2println(ints1)
println(ints1(5))
val ints2: List[Int] = 1 :: 2 :: 4 :: 5 :: Nil
val ints3: List[Int] = 3 :: 6 :: 7 :: 9 :: List()上述两行代码代表的是一个意思
Set 集合:
不可变 Set:
val value: Any = Set(1, 1, 2,2,3, 4, 5, 6, 7, 8, 9)println(value)运行结果:
判断set的类型:
val bool: Boolean = value.isInstanceOf[HashSet[Int]]println(bool)可变Set:
val ints: mutable.Set[Int] = mutable.Set(1, 2, 2, 3, 1, 4, 5, 6, 8, 7, 9)
可变Set的增加是add方法,不是append方法
可变Set的集合也是符合不可重复,不可修改的特点
只可增删查
Map集合:
map集合也是一个特质,可以通过apply方法创建对象
map是一个(k,v)集合
创建map:
(1)这是一种采用元组的方式创建的
val map = Map(("hello", 10), ("world", 20))
(2)这是采用的箭头的方式创建的
val map1 = Map("hello" -> 10, "world" -> 12)
常用第一种方式创建
map集合的遍历:
(采用第一种方式创建的)
for循环得到的对象是元组
for (elem <- map) {//elem是元组val key: String = elem._1val value: Int = elem._2println(s"${key}:${value}")}在Scala中value的类型为Int类型 在Java中是Int的包装类(防止在get方法找value不存在的时候为Null的情况)
上述情况也会在Scala中出现,Scala是对get方法使用Option(是一个抽象类,被两个子类实现(None,Some))封装
如果get的key存在 就调用上述的some类 再对结果进行调用get 转换成int类型 (方法很长,而且在没有值的情况下是会报错的)
因为太长引入了新的写法:
对map集合直接调用getOrElse(1)方法 设置1 有值输出值 无值输出1
val i: Int = map.getOrElse("hello", 1)println(i)不存在就会返回None
可变map:
可变map也是采用mutable.map进行创建
增删改查:
增加:
put方法 这个方法可以增加也可以进行修改 当key值存在的时候 如果value不同会覆盖前值
val maybeInt: Option[Int] = map.put("helloi2", 23)
删除:
val maybeInt1: Option[Int] = map.remove("hello")
查找:
查找与不可变一样使用getOrElse方法进行查找
元组:
本身为不可变 ,可以存放不同数据类型的元素
list具有上述的性质 但是使用list存放不同类型的数据 在调用的时候无法得到相应的类型(统一为Any)而tuple(元组可以)
tuple的定义:
val tuple: (String, Int) = ("hihihi", 23)
元组与map的关系:
map中的(key value )元素被默认当作二元组
特点:
这样我们可以实现list集合与map集合的转换
val toList: List[(String, Int)] = map1.toListprintln(toList)运行结果:

相关文章:

Scala之集合(1)
目录 集合介绍: 不可变集合继承图:编辑 可变集合继承图 数组: 不可变数组: 样例代码: 遍历集合的方法: 1.for循环 2.迭代器 3.转换成List列表: 4.使用foreach()函数&a…...

公网使用SSH远程登录macOS服务器【内网穿透】
文章目录前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址5. 使用固定TCP端口地址ssh远程前言…...
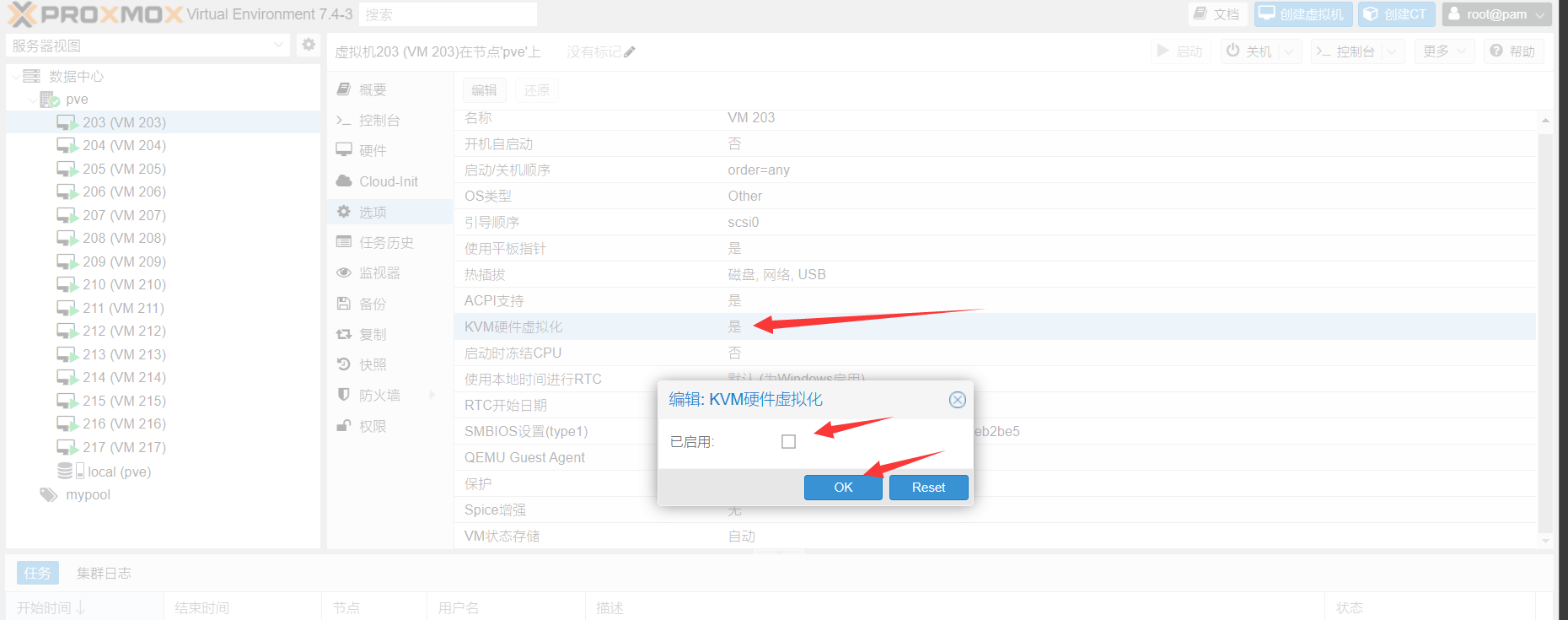
PVE相关的各种一键脚本(一键安装PVE)(一键开设KVM虚拟化的NAT服务器-自带内外网端口转发)
PVE 原始仓库:https://github.com/spiritLHLS/pve 前言 建议debian在使用前尽量使用最新的系统 非debian11可使用 debian一键升级 来升级系统 当然不使用最新的debian系统也没问题,只不过得不到官方支持 请确保使用前机器可以重装系统,…...
)
CSDN目录博客(zhaoshuangjian)
总目录 一、Java1.1 高并发1.2 多线程1.3 集合1.4 I/O1.5 异常1.6 事务1.7 锁机制1.8 JVM 二、数据库2.1 mysql2.1.1 mysql索引2.1.1 mysql锁2.1.1 mysql事务2.1.1 2.2 oracle2.3 postgresql2.4 达梦2.5 人大金仓kingbase 三、设计模式四、中间件4.1 缓存中间件-redis4.2 缓存中…...
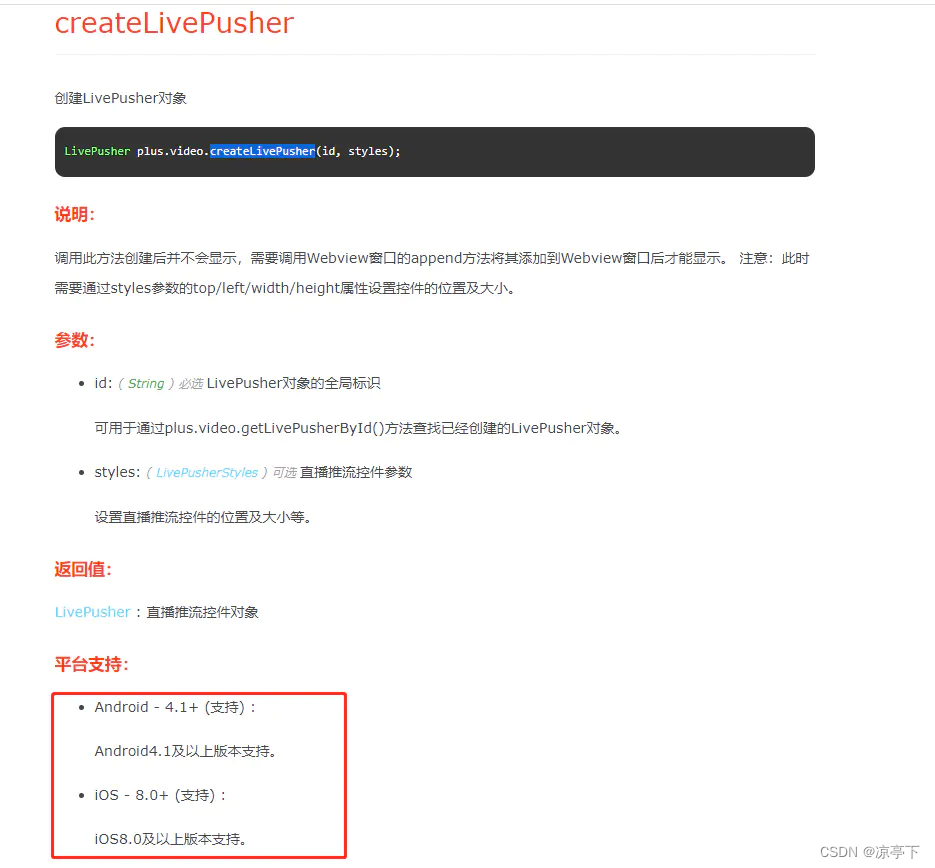
uniapp人脸识别解决方案
APP端: 因为APP端无法使用uni的camera组件,最开始考虑使用内嵌webview的方式,通过原生dom调用video渲染画面然后通过canvas截图。但是此方案兼容性在ios几乎为0,如果app只考虑安卓端的话可以采用此方案。后面又想用live-pusher组件…...

hashlib模块
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起探讨和分享Linux C/C/Python/Shell编程、机器人技术、机器学习、机器视觉、嵌入式AI相关领域的知识和技术。 hashlib模块专栏:《python从入门到实战》 哈希算法,也叫摘要算法。 加密&…...
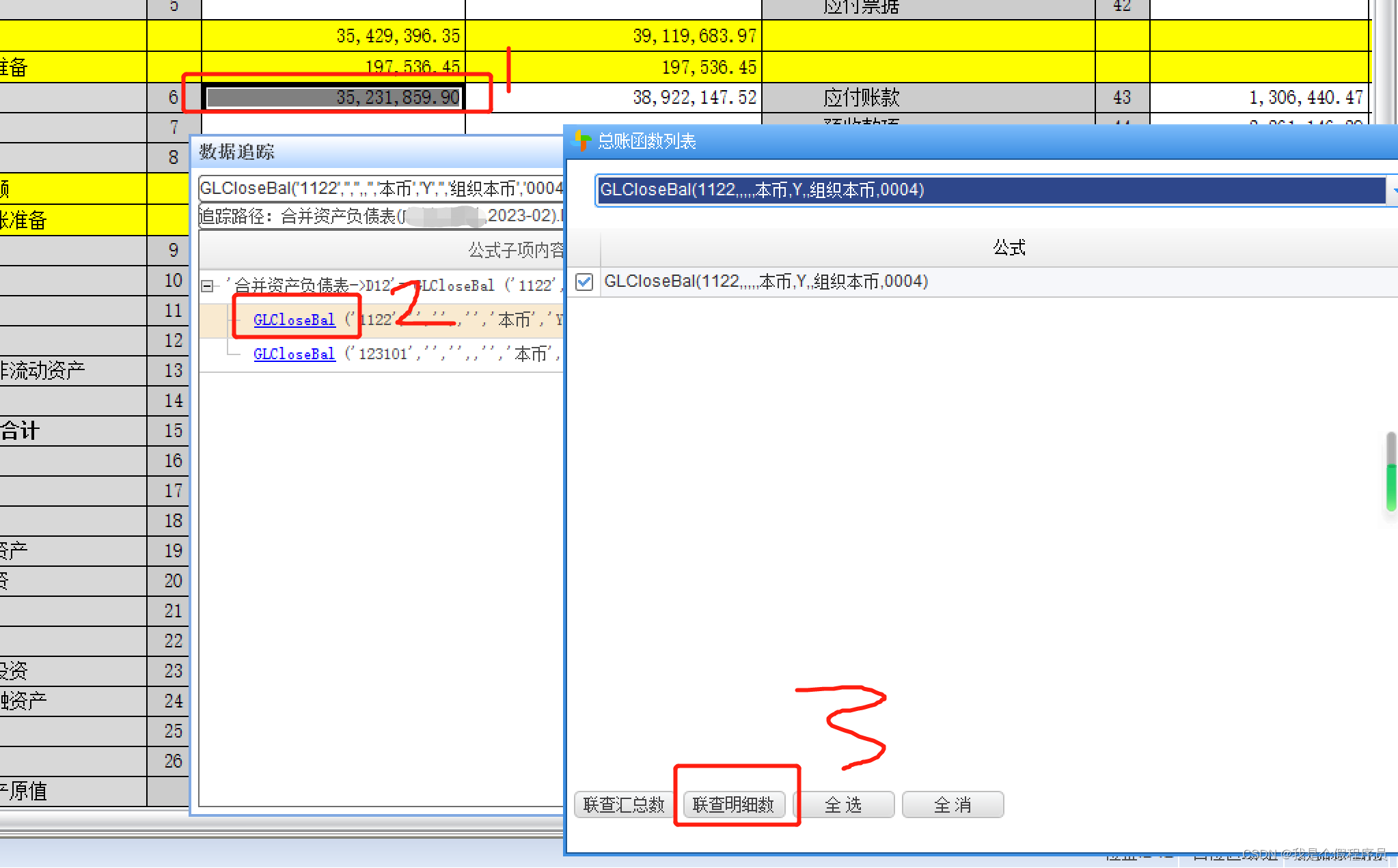
NC65合并报表如何取消上报并退回以及注意事项和相关问题总结
NC65合并报表如何取消上报并退回? 在【企业绩效管理】-【合并报表】-【合并】-【合并执行】节点中,点击〖数据中心〗按钮,在弹出的〖合并报表数据中心〗界面中,点击〖报送管理〗-〖合并方案请求退回〗,然后到【合并综…...

28岁,终于从字节退休了...
大厂一直是每个程序员都向往职业目标,大厂意味着薪资高、福利好、倍有面儿,而且发展空间也大。甚至有人调侃不想进大厂的程序员不是好程序员。 而在网上,也有各个网友分享自己在大厂的经历,在某平台还有一个近2600万浏览的话题&a…...
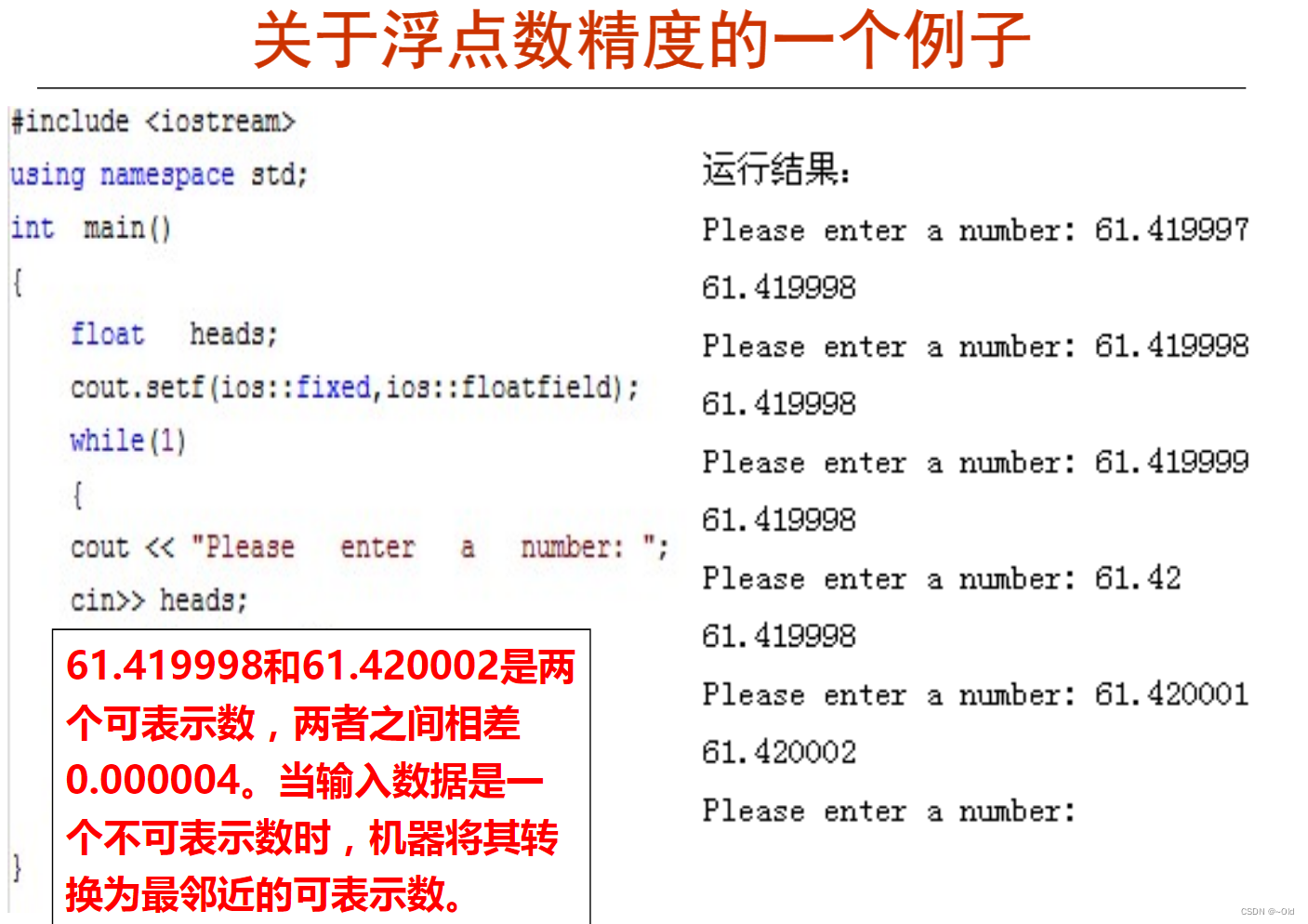
数据的表示和存储——
目录 浮点数的编码表示 浮点数类型 编辑 浮点数的表示 (1)浮点数(Float Point)的表示范围 (2)规格化数形式 (3)IEEE 754标准 其他形式的机器数表示 个人总结 浮点数的编码表…...
springboot零基础到项目实战
推荐教程: springboot零基础到项目实战 SpringBoot这门技术课程所包含的技术点其实并不是很多,但是围绕着SpringBoot的周边知识,也就是SpringBoot整合其他技术,这样的知识量很大,例如SpringBoot整合MyBatis等等。因此…...

自媒体都在用的5个素材网站,视频、音效、图片全部免费下载~
推荐几个自媒体必备的素材库,免费可商用,建议收藏! 1、菜鸟图库 视频素材下载_mp4视频大全 - 菜鸟图库 国内超大的素材库,在这里你可以找到设计、办公、图片、视频、音频等各种素材。视频素材就有上千个,全部都很高清…...

开放式耳机新巅峰!南卡OE Pro兼备澎湃音质、舒适佩戴、创新设计
众所周知,当初苹果带来TWS耳机新时代以后,后面有许多的蓝牙耳机相继跟随和模仿,但NANK南卡却独辟蹊径,将在近日重磅推出首款0压无感全开放无线耳机——南卡OE Pro,走向开放式TWS耳机的新时代。 31度黄金倾斜受力面&…...
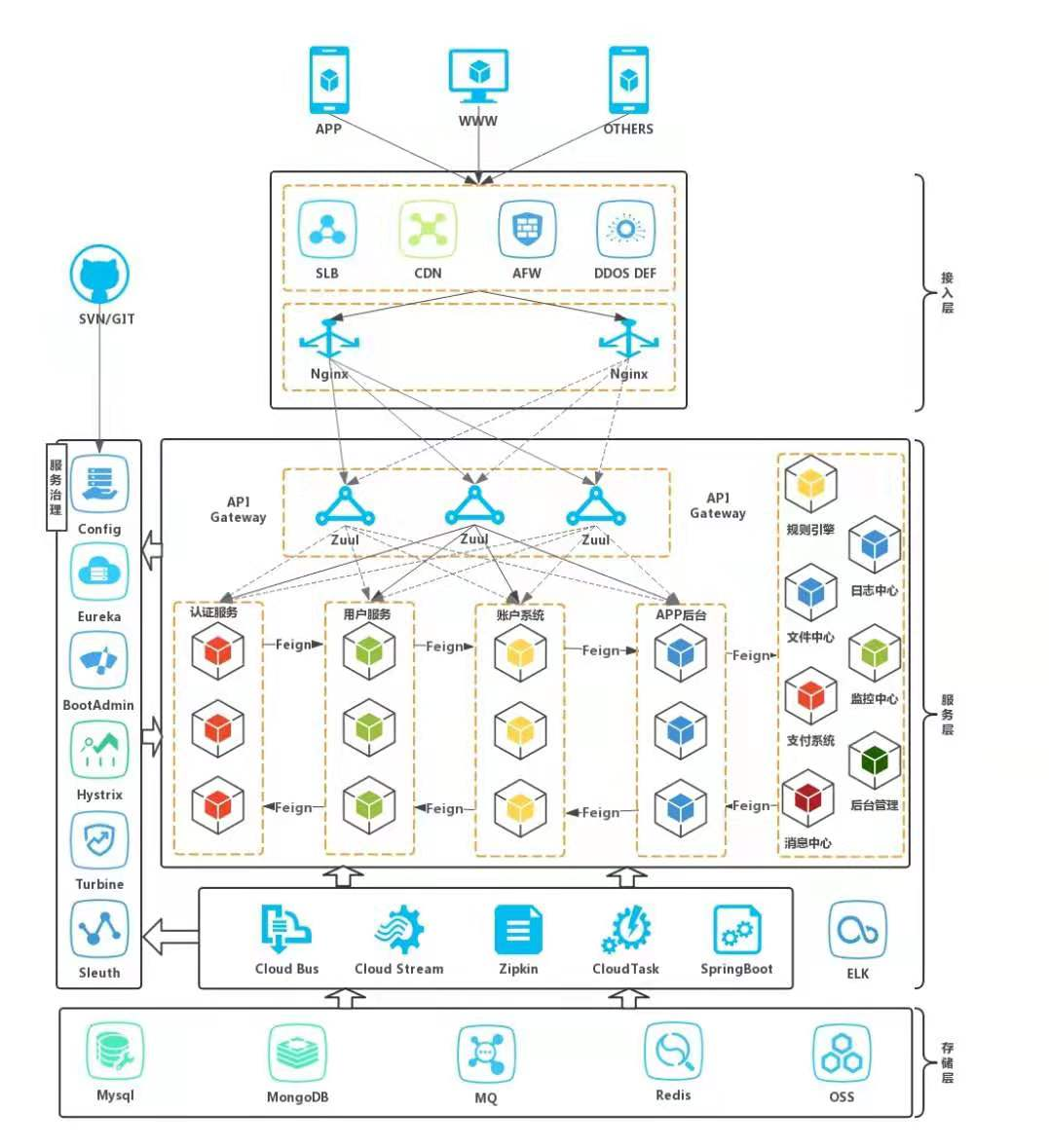
1700页,卷S人的 Java《八股文》PDF手册,涨薪跳槽拿高薪就靠它了
大家好,最近有不少小伙伴在后台留言,又得准备面试了,不知道从何下手! 不论是跳槽涨薪,还是学习提升!先给自己定一个小目标,然后再朝着目标去努力就完事儿了! 为了帮大家节约时间&a…...

普通人是否能从ChatGPT中分一杯羹?
ChatGPT3.0刚刚推出,最开始的时候,人们只是将ChatGPT看作一个很会聊天的机器人,无论问题多么天马行空,它的答案看上去都有理有据。后来,像打开潘多拉魔盒一样,很多人开始拿它编大纲、撰写文案、编代码、创作…...
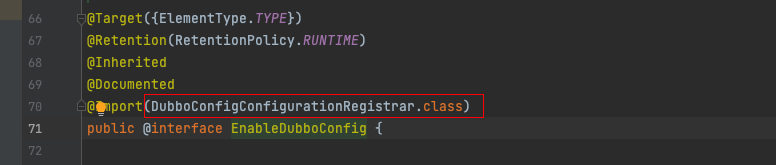
SpringBoot自动装配原理(附面试快速答法)
文章目录SpringBoot自动装配原理1. 从调用SpringApplication构造器方法开始2. 解析启动类4.按需装配4.1 分析dubbo自动装配5. 如果定义自己的starter6. 面试答法SpringBoot自动装配原理 之前面试被问到这个题目,只会答一些spi、AutoConfigration注解、Import之类的&…...
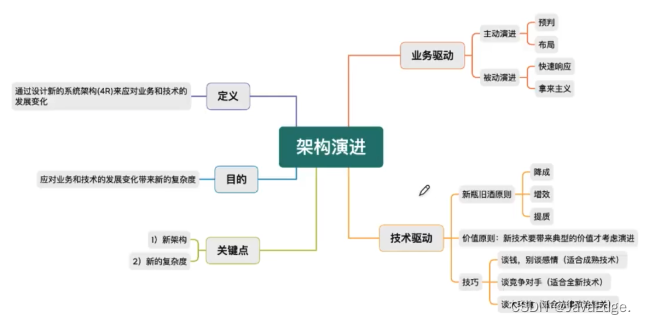
如何在大厂做好架构演进?
1 架构演进的定义 1.1 定义 通过设计新的系统架构(4R),来应对业务和技术的发展变化。 1.2 关键点 新架构新的复杂度 1.3 目的 应对业务和技术的发展变化后带来新的复杂度。 案例 淘宝去IOE,是因为业务发展大了后,IOE的成本和可控性难…...

减半技术实现求a的n次幂
目录 减半技术实现求a的n次幂 程序设计 程序分析 减半技术实现求a的n次幂 【问题描述】给定两个正整数a和n,采用减半技术求a的n次幂;其中a<100,b<20; 【输入形式】两个整数a,n(a与n中间用空格隔开); 【输出形式】一个整数 【样例输入1】2 3 【样例输出1】8 【样…...
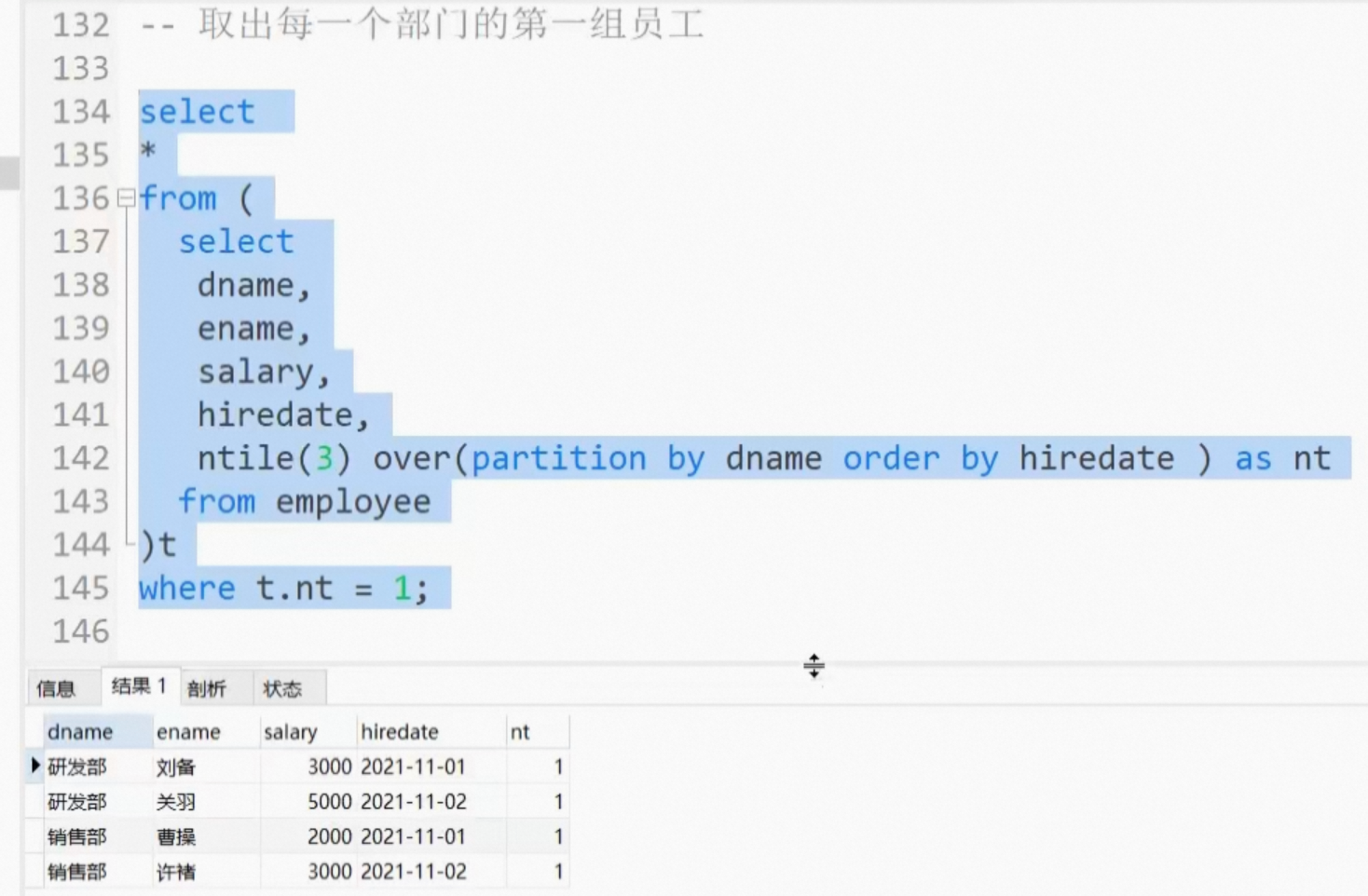
MYSQL8窗口函数
MYSQL8窗口函数 MYSQL8窗口函数窗口函数分类序号函数--排行榜row_number()示例rank()示例dense_rank()示例partition by对每个分区内的行进行排名不加partition by全局排序 开窗聚合函数分布函数CUME_DIST()PERCENT_RANK() 前后函数LAG()的用法LEAD() 头尾函数其他函数NTH_VALU…...
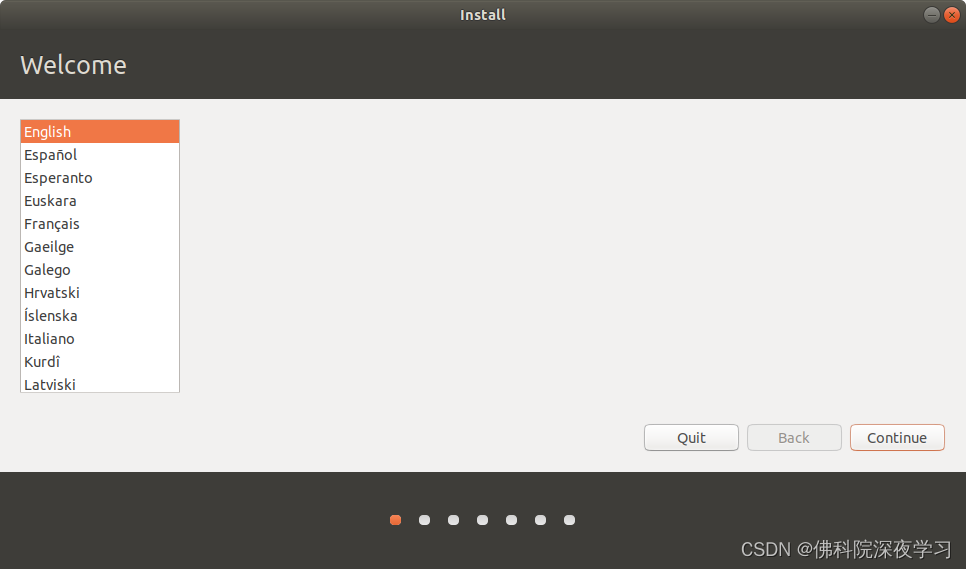
全国大学生智能汽车竞赛——安装Ubuntu操作系统(双系统)
1.1 电脑分区 1.1.1 分区原因 由于我们想要在电脑上同时安装Windows和Ubuntu系统,所以就要在window使用的内存中划分出来一段用来给Ubuntu系统使用,相当于一个应用程序一样 1.1.2 分区步骤 1.右击此电脑,点击管理,然后双击左侧…...
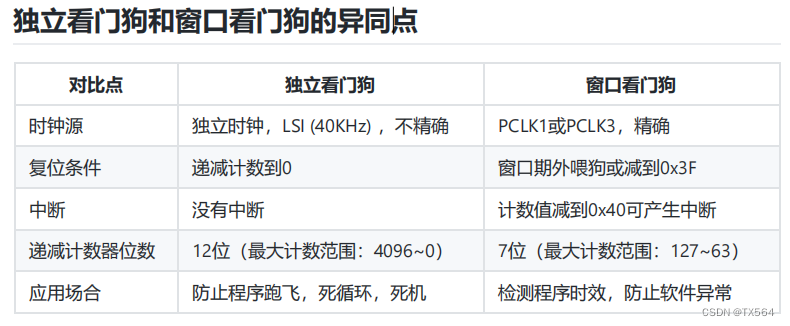
[STM32F103C8T6]看门狗
看门狗: 在由单片机构成的微型计算机系统中,由于单片机的工作常常会受到来自外界电磁场的干扰,造 成程序的跑飞,而陷入死循环,程序的正常运行被打断,由单片机控制的系统无法继续工作,会 造成整个…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
