数据的表示和存储——
目录
浮点数的编码表示
浮点数类型
编辑
浮点数的表示
(1)浮点数(Float Point)的表示范围
(2)规格化数形式
(3)IEEE 754标准
其他形式的机器数表示
个人总结
浮点数的编码表示
浮点数类型
| C语言声明 | 操作数类型 | 存储长度(位) |
|---|---|---|
| float | 单精度浮点数 | 32 |
| double | 双精度浮点数 | 64 |
| long double | 扩展精度浮点数 | 80 / 96 |
实数类型分为:单精度浮点,浮点双精度和扩展精度浮点
科学计数法(Scientific Notation) 与浮点数
从上面可以看出,对于一个实数都可以用一个定点整数和定点小数来表示,其中规格化的形式,小数点前面只有一个非0的数,对于二进制表示时,必定是1
浮点数的表示
(1)浮点数(Float Point)的表示范围
- 以下面的32位浮点数格式的规格化数为例,计算表示范围

1、第0位数代表符号位
2、第1~8位为8位移码表示阶码E(偏置常数为128)
3、第9~31位为24位二进制原码小数表示的尾数M(tips:注意这里定点小数表示尾数是采用的原码表示)
规格化尾数的小数点后第一位总是1,故规定第一位默认的1不明显的表示出来,这样可以用23位表示24位的尾数

因为原码对称,故其表示范围关于原点对称。可表示范围包括图中的阴影部分和0

机器0:即尾数为0或落在下溢区中的数
浮点数范围比定点数大,但数的个数没变多,故数之间更稀疏,且不均匀
(2)规格化数形式
为了能表示更多有效数字,通常规定规格化数的小数点前为1

32bit规格化数

其中:
1)S是符号位(Sign)
2) Exponent用移码表示(移码其实就是原码加上一个偏置常数)来表示
3)Significand表示xxxxxxxxxx(部分尾数)基可以是2/4/8/16,约定信息,无需显示表示
早期的计算机各自用自己的浮点数,这样会带来的结果是在不同的计算机中采用不同的格式解析数据,其实是不通用的,所以出现了IEEE754标准
(3)IEEE 754标准
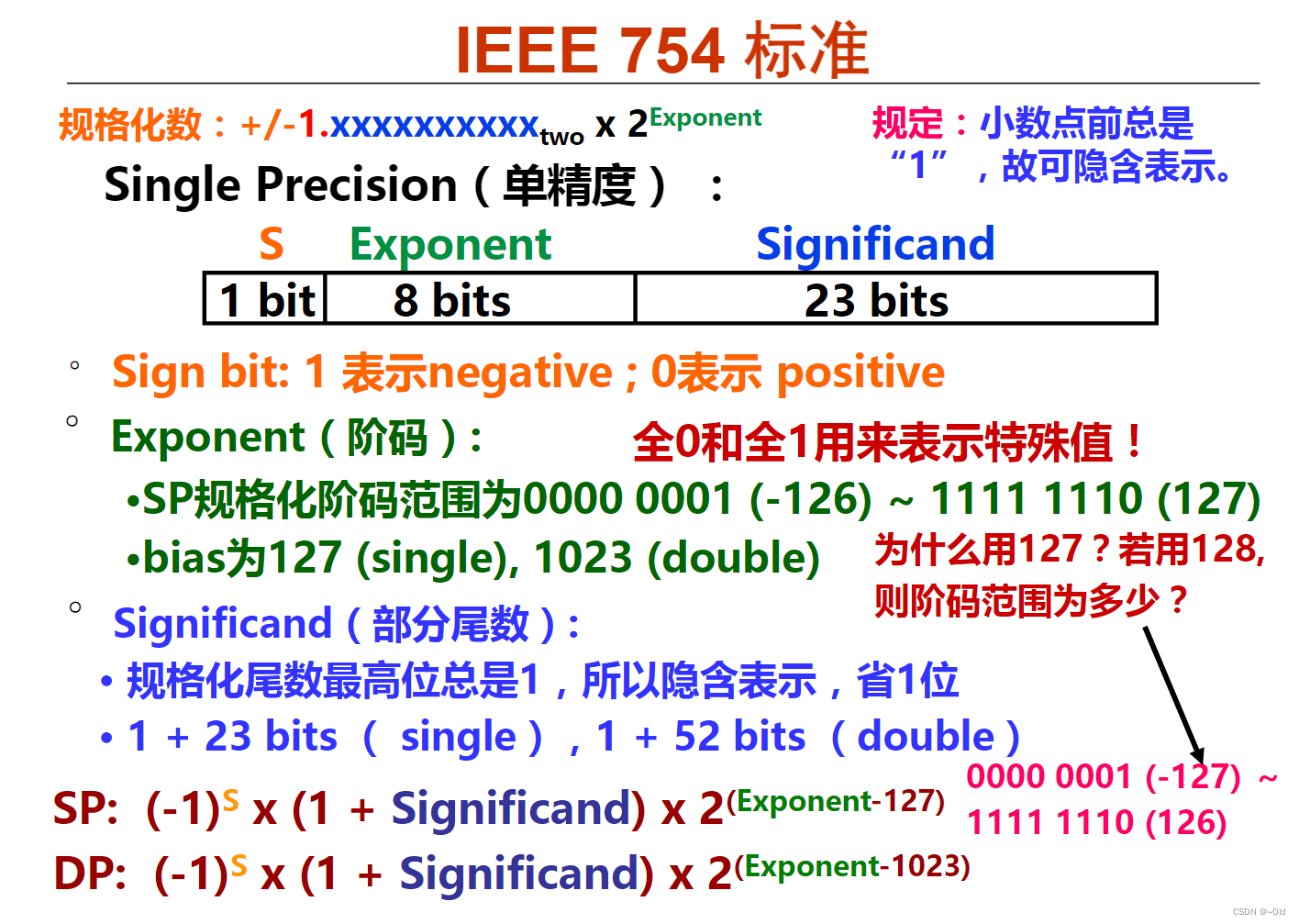
这里插入一个链接,讲解IEEE 754非常详细的一个博客
IEEE754标准: 一 , 浮点数在内存中的存储方式 - 知乎 (zhihu.com)
其中,需要注意的是上面的博客中没有指出阶码全0和全1是用来表示特殊情况的。
Q:为什么移码的偏置常数采用127而不是像之前的128
A: IEEE 754标准中,单精度浮点数可表示的范围是0000 0001(-126)~1111 1110(127);如果偏置常数采用的是128,则32位浮点数可表示的范围是0000 0001(-127)~1111 1110(126),2^-126~2^127比2^-127~2^126可表示的范围大
Q:已知float型变量x的机器数为BEE0 0000H,求x的值是多少?
A:转换为2进制,1 0111 1101 110 0000 0000 0000 0000 0000
符号位:1(负数)
阶码(指数):为避免混淆,用阶码表示阶的编码,用阶或者指数表示阶码的值
阶码:0111 1101B = 125
阶码的值:125-127 = -2(指数为-2)
尾数数值部分: 1 +1x2-1+ 1x2-2+ 0x2-3+ 0x2-4+ 0x2-5+… =1+2-1+2-2= 1+0.5 +0.25 = 1.75
所以真值是:-1.75x2^-2 = -0.4375
Q: 已知float型变量x的值为-12.75,求x的机器数是多少?
A: -12.75=-1100.11B =-1.10011B x 2^3符号S=1
阶码E=127+3=128+2=1000 0010
显式表示的部分尾数Significant = 100 1100 0000 0000 0000 0000(第一个1可以不用显示表示出来,因为规格化规定小数点前面一个数是非0的而且只有一位,必定是一个1)所以: x 的机器数表示为: 1 ,1000 0010, 100 1100 0000 0000 0000 0000
转换为十六进制表示为:C14C0000H
其他形式的机器数表示
前面定义的是针对规格化形式(normalized form)的数,那么,其他形式的机器数表示什么样的信息呢?
(1)0的机器数表示
0其实就是尾数部分和阶码部分都是为0的,不同的符号位表示+0和-0,二者都是有效的
How to represent 0?
exponent: all zeros
significand: all zeros
What about sign?Both cases valid.
+0: 0 00000000 00000000000000000000000
-0: 1 00000000 00000000000000000000000
(2)+∞/-∞的机器数表示
无穷其实就是阶码全为1,其中尾数部分全为0,不同的符号位表示正无穷和负无穷
浮点数除0的结果是+/-∞, 而不是溢出异常.(整数除0为异常)
为什么要这样处理? 可以利用+∞/-∞作比较。例如:X/0>Y可作为有效比较
How to represent +∞/-∞?
Exponent: all ones (11111111B = 255)
Significand: all zeros
+∞: 0 11111111 00000000000000000000000
-∞: 1 11111111 00000000000000000000000
(3)“非数”的表示(NaN)
非数,这个错误其实在编写程序的时候也是经常遇到的一种情况,其中非数就是阶码全为1,尾数部分不为0的情况
例如“Sqrt (-4.0) ”,“0/0”等的结果称为Not a Number (NaN) ,即“非数”
NaNs 可以帮助调试程序
How to represent NaN ?
Exponent: 255
Significand: nonzero
4. 非规格化数(Denorms)的表示
除了上面的三种情况,其实只剩下一种,就是阶码全为0,尾数部分不为0,这表示的就是非规格化数
How to represent Denorms?
Exponent: 0
Significand: nonzero
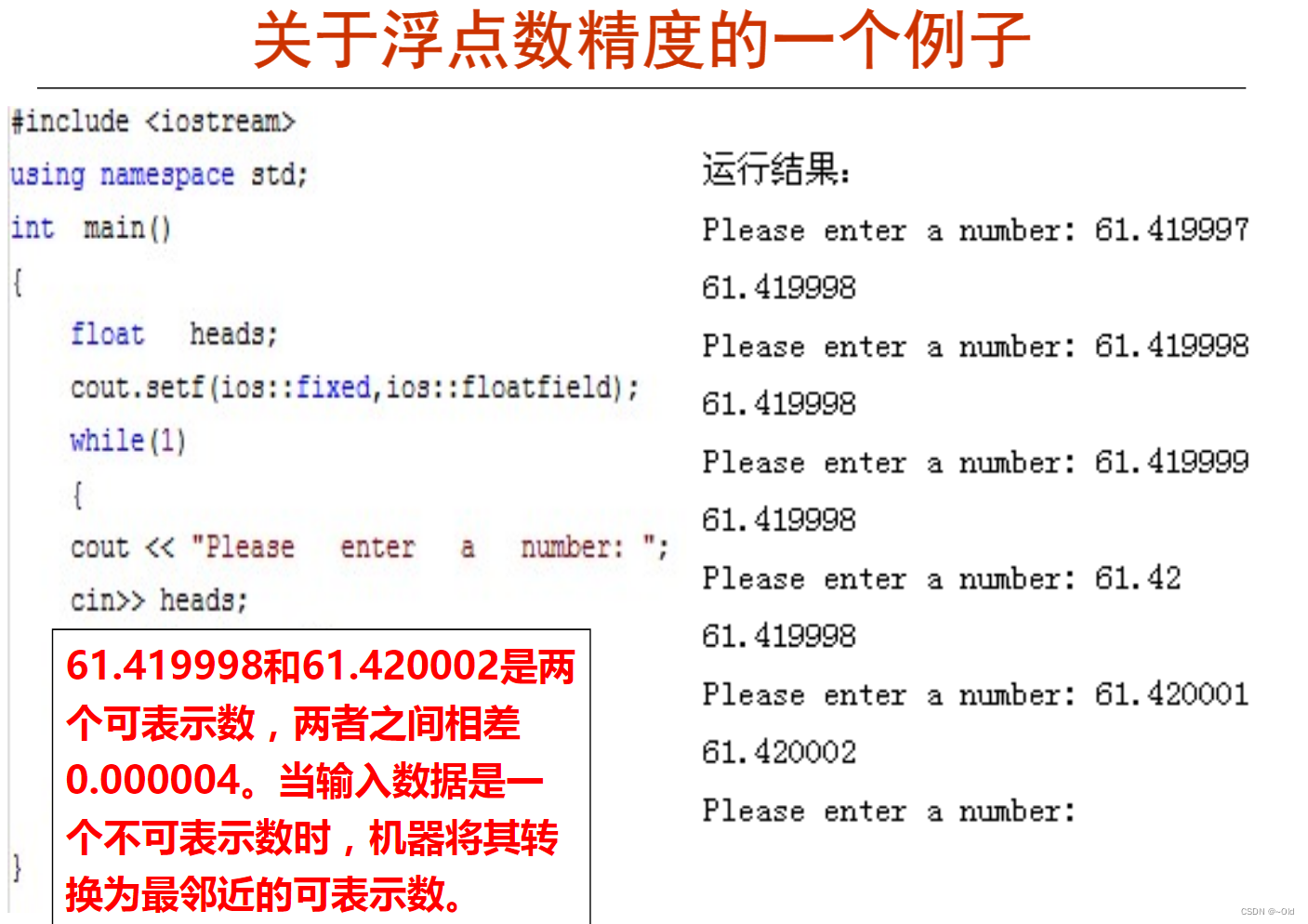
这张图,其实包含了很多信息,其中用规格化数表示浮点数其实不能表示完全,比如最小的整数用规格化数表示其实就是上面图中的1.0000....x2^-126,对于比如说2^-125~2^-124和2^-124~2^-123,其中后者长度是前者的两倍,但是由于尾数部分的位数是固定的,其实二者之间可以表示的数据的个数是一样的,都是2^23个,所以对于浮点数来说,数据越大,可以表示的最近的两个浮点数的距离是越来越大的,数据越小其实可以表示的数据精度越高,越有可能可以精确表示,但是数字越大,由于可以表示的数字间距越来越大,所以表示的就可能更不精确,这也是为什么我之前一直不知道为什么计算机不能表示任意的浮点数,比如0.1+0.2不是0.3会有偏差的原因,就是不能表示0.3只能取离它最近的一个浮点数来表示。
个人总结
1、任何一个实数都可以用一个定点整数和一个定点小数来表示,其中定点整数其实就是指的整数(来表示科学计数法中的指数部分),定点小数一般表示科学计数法中的小数部分(尾数)。
2、浮点数是有精度的,之前是不知道为什么有的浮点数在计算机中是没有办法存储和表示的,只能根据某个特定的规则进行舍入和表示,而且浮点数数字越小越有可能精确表示,对于浮点数越大,精确表示的可能就越小,因为数越大,可表示的两个浮点数之间的距离越来越大。
3、浮点数采用科学计数法,只需要定点小数表示尾数(采用原码)和定点整数表示指数部分就可以表示任意一个浮点数
4、IEEE 754标准的一个好的博客
IEEE754标准: 一 , 浮点数在内存中的存储方式 - 知乎 (zhihu.com)
相关文章:

数据的表示和存储——
目录 浮点数的编码表示 浮点数类型 编辑 浮点数的表示 (1)浮点数(Float Point)的表示范围 (2)规格化数形式 (3)IEEE 754标准 其他形式的机器数表示 个人总结 浮点数的编码表…...
springboot零基础到项目实战
推荐教程: springboot零基础到项目实战 SpringBoot这门技术课程所包含的技术点其实并不是很多,但是围绕着SpringBoot的周边知识,也就是SpringBoot整合其他技术,这样的知识量很大,例如SpringBoot整合MyBatis等等。因此…...

自媒体都在用的5个素材网站,视频、音效、图片全部免费下载~
推荐几个自媒体必备的素材库,免费可商用,建议收藏! 1、菜鸟图库 视频素材下载_mp4视频大全 - 菜鸟图库 国内超大的素材库,在这里你可以找到设计、办公、图片、视频、音频等各种素材。视频素材就有上千个,全部都很高清…...

开放式耳机新巅峰!南卡OE Pro兼备澎湃音质、舒适佩戴、创新设计
众所周知,当初苹果带来TWS耳机新时代以后,后面有许多的蓝牙耳机相继跟随和模仿,但NANK南卡却独辟蹊径,将在近日重磅推出首款0压无感全开放无线耳机——南卡OE Pro,走向开放式TWS耳机的新时代。 31度黄金倾斜受力面&…...
1700页,卷S人的 Java《八股文》PDF手册,涨薪跳槽拿高薪就靠它了
大家好,最近有不少小伙伴在后台留言,又得准备面试了,不知道从何下手! 不论是跳槽涨薪,还是学习提升!先给自己定一个小目标,然后再朝着目标去努力就完事儿了! 为了帮大家节约时间&a…...

普通人是否能从ChatGPT中分一杯羹?
ChatGPT3.0刚刚推出,最开始的时候,人们只是将ChatGPT看作一个很会聊天的机器人,无论问题多么天马行空,它的答案看上去都有理有据。后来,像打开潘多拉魔盒一样,很多人开始拿它编大纲、撰写文案、编代码、创作…...
SpringBoot自动装配原理(附面试快速答法)
文章目录SpringBoot自动装配原理1. 从调用SpringApplication构造器方法开始2. 解析启动类4.按需装配4.1 分析dubbo自动装配5. 如果定义自己的starter6. 面试答法SpringBoot自动装配原理 之前面试被问到这个题目,只会答一些spi、AutoConfigration注解、Import之类的&…...
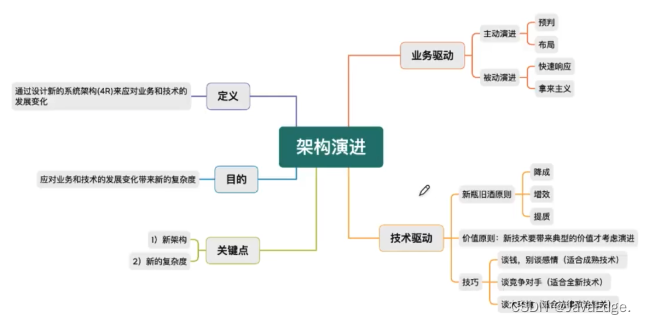
如何在大厂做好架构演进?
1 架构演进的定义 1.1 定义 通过设计新的系统架构(4R),来应对业务和技术的发展变化。 1.2 关键点 新架构新的复杂度 1.3 目的 应对业务和技术的发展变化后带来新的复杂度。 案例 淘宝去IOE,是因为业务发展大了后,IOE的成本和可控性难…...

减半技术实现求a的n次幂
目录 减半技术实现求a的n次幂 程序设计 程序分析 减半技术实现求a的n次幂 【问题描述】给定两个正整数a和n,采用减半技术求a的n次幂;其中a<100,b<20; 【输入形式】两个整数a,n(a与n中间用空格隔开); 【输出形式】一个整数 【样例输入1】2 3 【样例输出1】8 【样…...
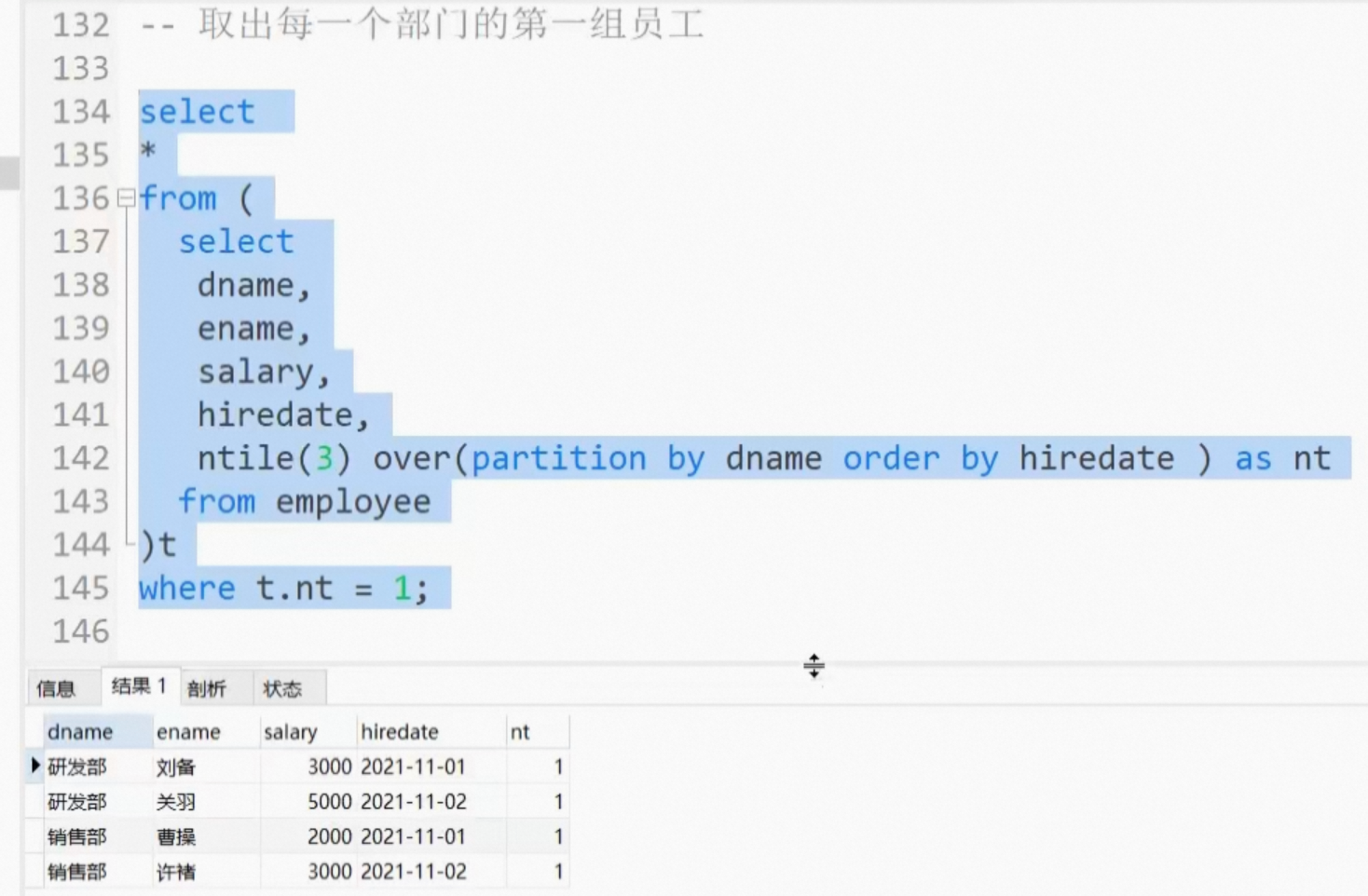
MYSQL8窗口函数
MYSQL8窗口函数 MYSQL8窗口函数窗口函数分类序号函数--排行榜row_number()示例rank()示例dense_rank()示例partition by对每个分区内的行进行排名不加partition by全局排序 开窗聚合函数分布函数CUME_DIST()PERCENT_RANK() 前后函数LAG()的用法LEAD() 头尾函数其他函数NTH_VALU…...
全国大学生智能汽车竞赛——安装Ubuntu操作系统(双系统)
1.1 电脑分区 1.1.1 分区原因 由于我们想要在电脑上同时安装Windows和Ubuntu系统,所以就要在window使用的内存中划分出来一段用来给Ubuntu系统使用,相当于一个应用程序一样 1.1.2 分区步骤 1.右击此电脑,点击管理,然后双击左侧…...
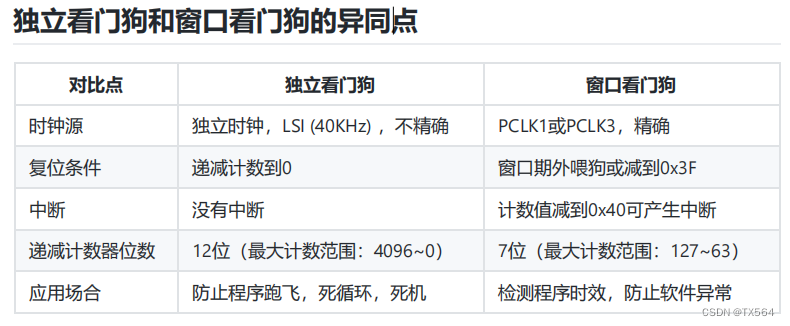
[STM32F103C8T6]看门狗
看门狗: 在由单片机构成的微型计算机系统中,由于单片机的工作常常会受到来自外界电磁场的干扰,造 成程序的跑飞,而陷入死循环,程序的正常运行被打断,由单片机控制的系统无法继续工作,会 造成整个…...

浪潮:2022年净利同比增长51.39%
一、4月头条 华为的紧急回应,让东方材料21亿收购要黄? 4月10日消息,东方材料昨日晚间公告拟定增募资不超20亿元,用于向诺基亚全资子公司NSN收购TD TECH 51%股权(交易对价21.22亿元)。TD TECH剩余49%股权由…...

大厂面试内幕:阿里内部整理出的5000页Java面试复盘指南,起飞!!!
互联网的技术岗一直是高薪的代名词,特别是大厂,应届生的年薪基本都20W起,比一般的公司高多了。 看下面这张网上热传的大厂应届生薪酬表就知道了,SP offer甚至能拿到30W以上。 技术社区也有晒出高薪offer的同学: 除了薪…...

数据结构——哈希表相关题目
数据结构——哈希表相关题目 242. 有效的字母异位词1.暴力解法2.排序后比较3.哈希表 383. 赎金信哈希解法 49. 字母异位词分组438. 找到字符串中所有字母异位词3. 无重复字符的最长子串76. 最小覆盖子串349. 两个数组的交集1.排序双指针2.哈希表 350. 两个数组的交集 II1.排序双…...
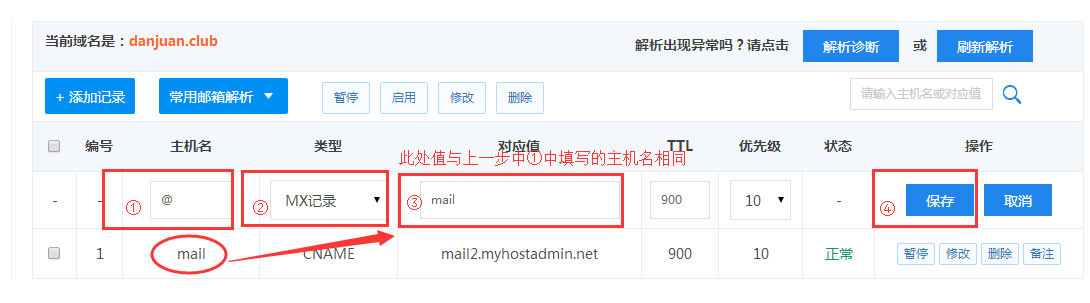
域名解析设置方法
域名解析设置都是实时生效的,一般只需几秒即可同步到各地 DNS 上,但各地 DNS 均有缓存机制,解析的最终生效取决于各运营商刷新时间! 一、A记录 ①.主机名必须填写; 常用主机名有:www//*,效果参见上图说明&…...

MySQL连接空闲时间超过8小时报错原因与延伸知识
1 错误原因 1.1 两个参数 MySQL服务端两个参数控制连接超时时间: wait_timeoutinteractive_timeout1.1.1 如何查看 show global variables like interactive_timeout show global variables like wait_timeout 复制代码 1.1.2 含义与区别 wait_timeout…...
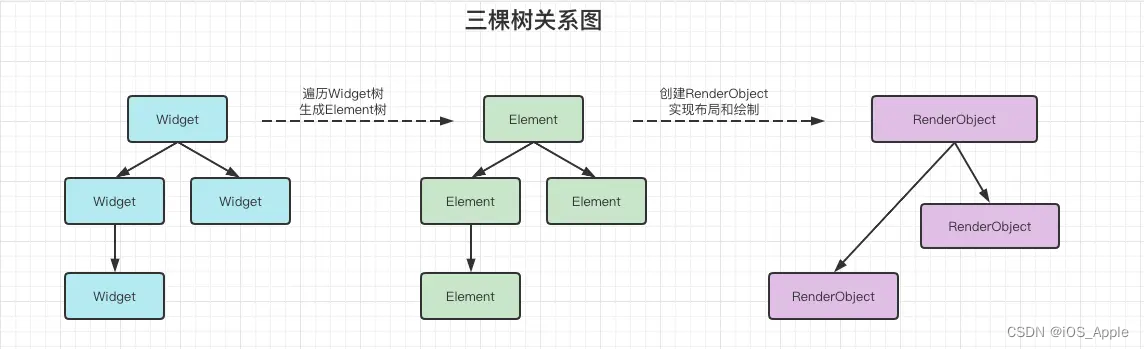
Flutter渲染原理
一 Widget Element RenderObject 之间的关系 1 Widget 在Flutter 中,万物皆是Widget,无论是可见的还是功能型的。一切都是Widget. 官方文档中说的Widget 使用配置和状态来描述View 界面应该长什么样子。 它不仅可以表示UI元素,也可以表示一些功能性的…...
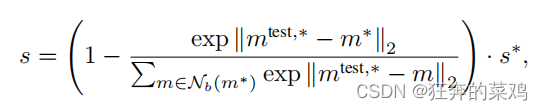
PathCore:IAD文献解读
论文链接:[Towards Total Recall in Industrial Anomaly Detection]Towards Total Recall in Industrial Anomaly Detection :数据集, :标签 : 在ImageNet上预训练后的网络 第 张图 网络中第 层 1. Locall…...

C语言判断一个日期是在该年的第几天案例讲解
今天是2023年4月11号,我们就用今天举例得出是2023年的第几天。 思路分析 1)我们想知道2023年4月11号是2023年的第几天,只需要把1到3月份的天数累加求和然后加上今天日期也就是11就可以算出2023年4月11号是2023年的第几天。 推广:…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

