LeetCode 785. Is Graph Bipartite【DFS,二分图】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:
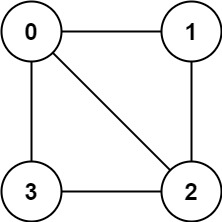
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:
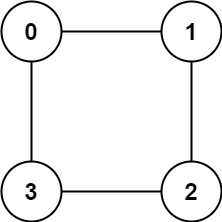
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n1 <= n <= 1000 <= graph[u].length < n0 <= graph[u][i] <= n - 1graph[u]does not containu.- All the values of
graph[u]are unique. - If
graph[u]containsv, thengraph[v]containsu.
题意:存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
- 不存在自环(
graph[u]不包含u)。 - 不存在平行边(
graph[u]不包含重复值)。 - 如果
v在graph[u]内,那么u也应该在graph[v]内(该图是无向图) - 这个图可能不是连通图,也就是说两个节点
u和v之间可能不存在一条连通彼此的路径。
二分图 定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为 二分图 。
如果图是二分图,返回 true ;否则,返回 false 。
解法 DFS染色判断二分图
二分图的节点可以分成两个集合,集合内的点之间没有边,任意一条边的两个节点属于不同集合,可以为图中各个节点着色,两个集合的节点分别涂成两种颜色。如果图中任何一条边的两个节点都可以被涂成不同的颜色,则该图就为二分图。
一个图可能包含多个子图,需要逐次对每个子图涂色。需要一个数组 colors 标记所有节点的颜色,规定 0 0 0 表示当前未涂色, 1 1 1 表示第一种颜色, 2 2 2 表示第二种颜色。为了给所有的节点着色,需要遍历图内的所有结点,在着色的过程中若碰到「已着色、但不符合一条边两个节点不同颜色」的情况,即可判断该图不可能是二分图。
遍历图的所有结点可以使用两种方式,即广度优先搜索和深度优先搜索。这里用DFS,比较简洁:
class Solution {
public:bool isBipartite(vector<vector<int>>& graph) {int n = graph.size();vector<int> color(n);function<bool(int, int)> dfs = [&](int i, int c) {color[i] = c; // 1,2表示访问过,0表示未访问for (int j : graph[i]) {if (!color[j] && dfs(j, 3 - c) == false) return false;else if (color[j] == color[i]) { return false; }}return true;};for (int i = 0; i < n; ++i)if (!color[i] && dfs(i, 1) == false) return false;return true;}
};
相关文章:

LeetCode 785. Is Graph Bipartite【DFS,二分图】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【微信小程序】-- 分包 - 独立分包 分包预下载(四十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

2.3 连续性随机变量
思维导图: 学习目标: 我会按照以下步骤学习连续型随机变量: 复习概率论的基础知识,包括概率、期望、方差等概念和公式,以及离散型随机变量的概率分布函数和概率质量函数的概念和性质。 学习连续型随机变量的概念和性…...
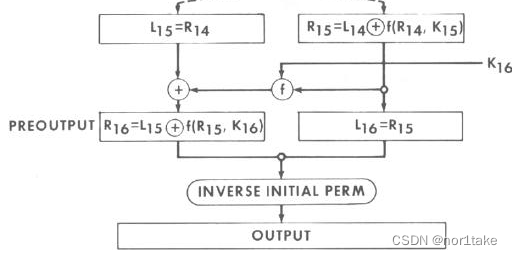
【DES详解】(一)处理input block(64 bits)
一、DES 加密算法总览 0-1、初识置换 IP(Initial Permutation) 输入:明文(64 bits) 过程:初识置换 输出:处理后的明文permuted input(64 bits) 首先,对需要解…...

redis笔记——三种特殊的数据结构
三种特殊数据类型 geospatial(地理位置) 用于定位,附近的人,距离计算 添加元素 geoadd key 经度 纬度 描述名称,可一次添加多个元素 127.0.0.1:6379> geoadd china:city 113.28 23.12 guangzhou (integer) 1 1…...

网络安全之编码加密算法
网络安全之编码加密算法 一、ROT5/13/18/47编码转换二、MD5加密 一、ROT5/13/18/47编码转换 ROT5、ROT13、ROT18、ROT47 编码是一种简单的码元位置顺序替换暗码,属于凯撒密码的一种。此类编码具有可逆性,可以自我解密,主要用于应对快速浏览&…...

mp4视频无法播放的解决方法
mp4视频是我们日常工作生活中经常会遇到的视频格式,但如果遇到重要的mp4视频无法播放了,该怎么办呢?有mp4视频无法播放的解决方法吗?下面小编为大家整理了这个问题产生的原因以及相应的解决方法,让我们看一看。 什么情况下会导致mp4视频无法…...

搭建Mysql
登录root账号 su root #上传 mysql-advanced-5.7.17-linux-glibc2.5-x86_64.tar.gz #创建mysql的用户组/用户, data目录及其用户目录 groupadd mysql useradd -g mysql -d /home/mysql mysql mv mysql-advanced-5.7.17-linux-glibc2.5-x86_64 mysql mkdir /home/mysql/data…...

气传导和骨传导耳机哪个好?简单科普这两种蓝牙耳机
在生活中,我们经常会用到耳机,特别是在日常娱乐听歌、运动休闲、户外通勤的时候,一款舒适的耳机是必不可少的。 而最近几年,随着科技的发展,各大品牌也相继推出了各种类型的耳机,其中比较热门的就有气传导…...
浅尝GoWeb开发之Gin框架
一、框架简介 gin 目前应用最广泛的golang框架,甚至已经变成了golang的官方框架,但它主要是一个RESTFul的框架。封装比较优雅,API友好,源码注释比较明确。个人比较推荐。 beego 国内最早的golang框架,也是最全的MV…...

工程行业管理系统-专业的工程管理软件-提供一站式服务
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示1…...
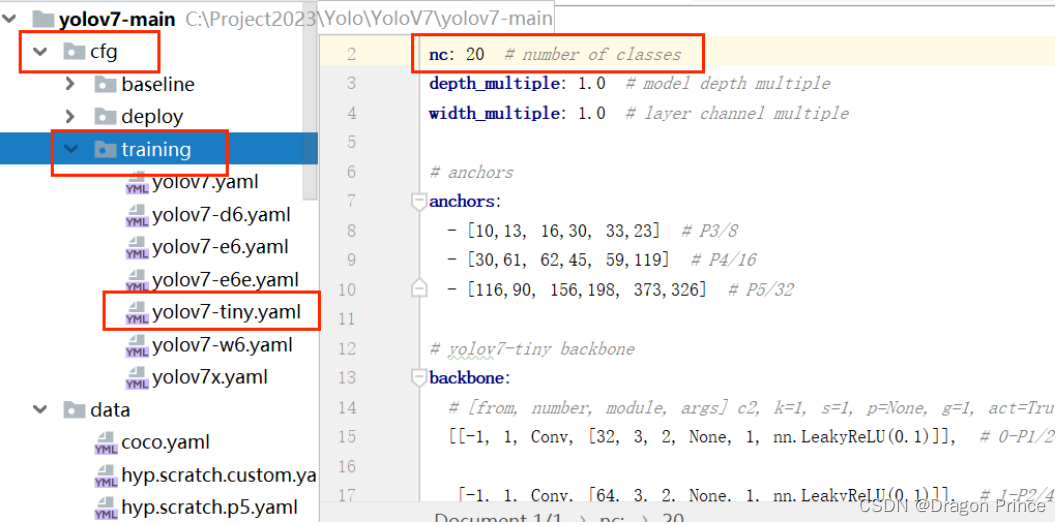
目标检测YOLO系列-YOLOV7运行步骤(推理、训练全过程)
下载源代码:点击下载 进入项目根目录并执行以下命令安装requirements.txt中的相关依赖 pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple官网下载权重yolov7.pt(测试使用)、yolov7-tiny.pt(训练使用…...
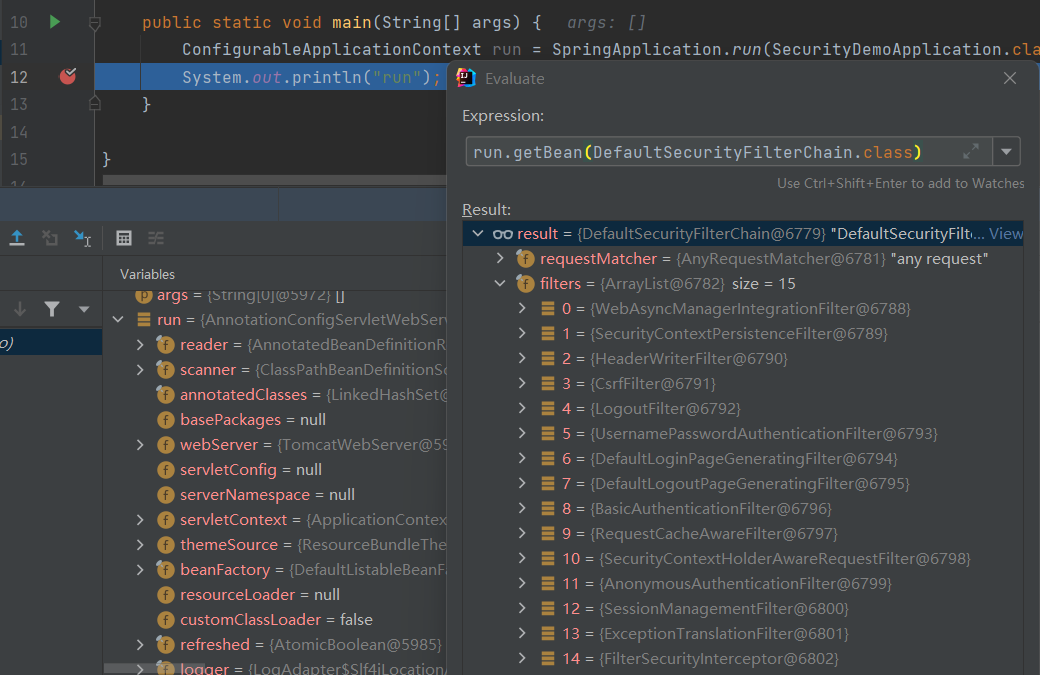
Spring Boot + Spring Security基础入门教程
Spring Security简介 Spring Security 是一个功能强大且高度可定制的身份验证和访问控制框架。Spring Security 致力于为 Java 应用程序提供身份验证和授权的能力。 Spring Security 两大重要核心功能:用户认证(Authentication)和用户授权&am…...

MySQL数据库,表的增删改查详细讲解
目录 1.CRUD 2.增加数据 2.1创建数据 2.2插入数据 2.2.1单行插入 2.2.2多行插入 3.查找数据 3.1全列查询 3.2指定列查询 3.3查询字段为表达式 3.3.1表达式不包含字段 3.3.2表达式包含一个字段 3.3.3表达式包含多个字段 3.4起别名 3.5distinct(去重) 3.6order …...
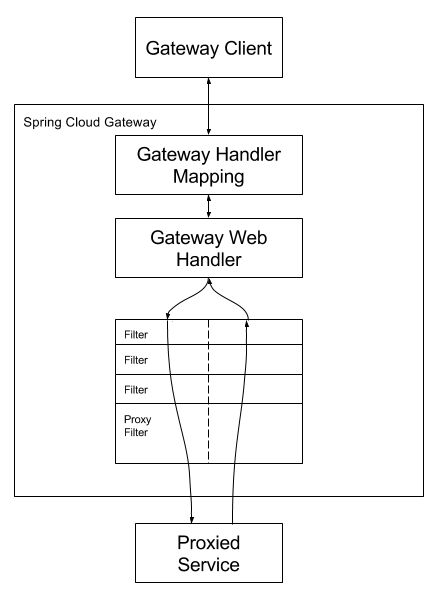
SpringCloud-Gateway实现网关
网关作为流量的入口,常用的功能包括路由转发、权限校验、限流等 Spring Cloud 是Spring官方推出的第二代网关框架,由WebFluxNettyReactor实现的响应式的API网关,它不能在传统的servlet容器工作,也不能构建war包。基于Filter的方式…...

Redis 如何配置读写分离架构(主从复制)?
文章目录 Redis 如何配置读写分离架构(主从复制)?什么是 Redis 主从复制?如何配置主从复制架构?配置环境安装 Redis 步骤 通过命令行配置从节点通过配置文件配置从节点Redis 主从复制优点Redis 主从复制缺点 Redis 如何…...

代码随想录二刷day05 | 哈希表之242.有效的字母异位词 349. 两个数组的交集 202. 快乐数 1. 两数之和
当遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了 二刷day05 242.有效的字母异位词349. 两个数组的交集202. 快乐数1. 两数之和 242.有效的字母异位词 题目链接 解题思路: class Solution { public:bool isAnagram(string s, string…...

2023年4月广东省计算机软考中/高级备考班招生简章
软考是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资格考试。 系统集成…...
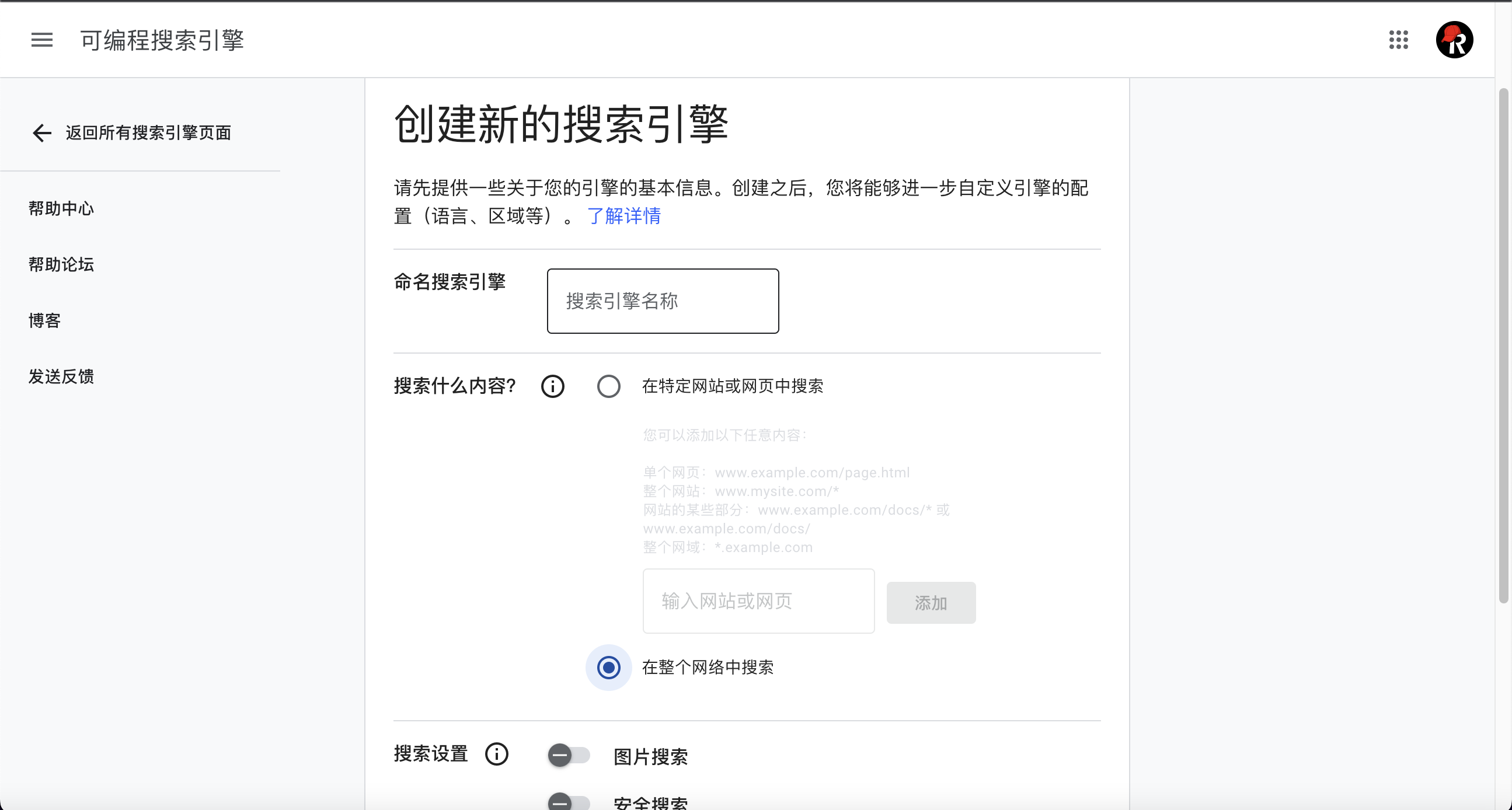
在Github中77k星的王炸AutoGPT,会独立思考,直接释放双手
文章目录 1 前言1.1 什么是AutoGPT1.2 为什么是AutoGPT 2 AutoGPT部分实例2.1 类似一个Workflow2.2 市场调研2.3 自己写播客2.4 接入客服 3 安装和使用AutoGPT3.1 安装3.2 基础用法3.3 配置OpenAI的API3.4 配置谷歌API3.5 配置Pinecone API 4.讨论 1 前言 迄今为止,…...
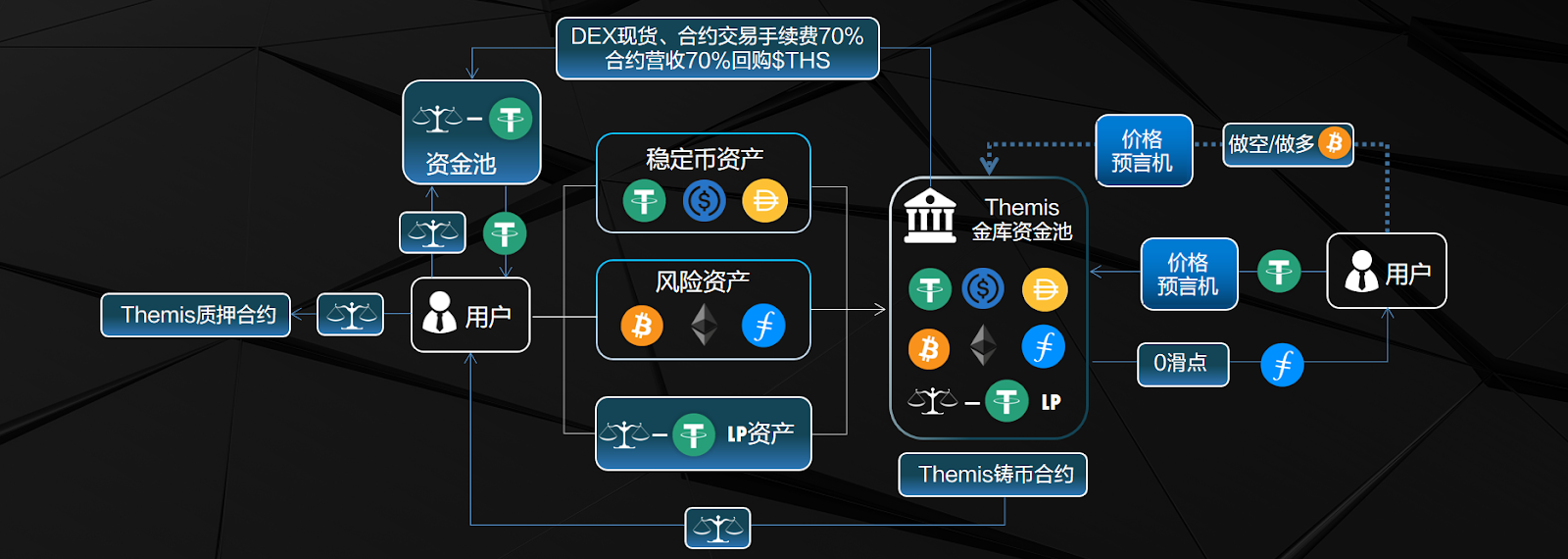
FVM链的Themis Pro,5日ido超百万美元
交易一直是 DeFi 乃至web3领域最经久不衰的话题,也因此催生了众多优秀的去中心化协议,如 Uniswap 和 Curve。这些协议逐渐成为了整个系统的基石。 在永续合约方面,DYDX 的出现将 WEB2 时代的订单簿带回了web3。其链下交易的设计,仿…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
