GD(兆易创新)系列FLASH进行FPGA和ZYNQ配置固化相操作
写在前面
本文主要针对使用GD(兆易创新)系列的FLASH做启动配置片时,遇到的相关问题进行简单整理复盘,避免后人踩坑。
本人操作固化芯片型号为:ZYNQ7045、690T(复旦微替代型号V7 690T)。
7系列FPGA固化
由于GD SPI Flash器件和进口器件的厂家ID不一致,而Vivado软件又不支持跳过ID检查,导致使用GD Flash做FPGA配置片时,无法通过Vivado软件直接烧录。
常见方法有两个,一个是通过TCL脚本加自定义桥接位流的方式,另外一个是通过ISE的IMPACT调过核查ID的操作。
通过TCL脚本加自定义桥接位流的方式,在Vivado平台上实现对FLASH配置片的直接烧录。该方法工作量较大,且不同国产芯片的相关修改配置不同,很难做到兼容处理,且需要相关公司的技术部门对相关操作(如烧写FLASH的相关文件进行替换)进行完善处理,操作难度较大。
通过ISE的IMPACT跳过核查ID的操作,只需要安装ISE版本(推荐安装14.7)的软件,添加环境变量进行固化操作即可。
添加跳过IDCODE核查环境变量
安装xilinx ISE14.7后,打开电脑的环境变量,配置IMPACT跳过ID核查,变量名输入:XIL_IMPACT_SKIPIDCODECHECK,变量值设置为1。
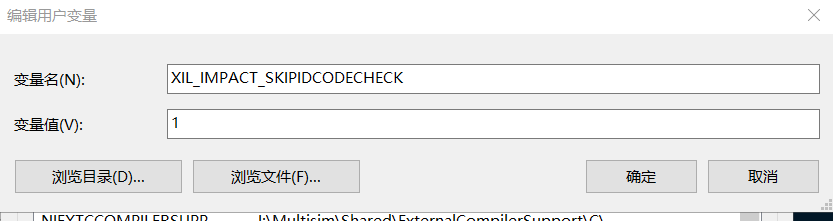
完成设置后重启电脑即可生效。
制作MCS文件
找到ISE的IMPACT,双击创建PROM文件,如选择SPI器件,如图示操作进行选择FLASH固化文件的配置。

点击OK后弹出以下界面。
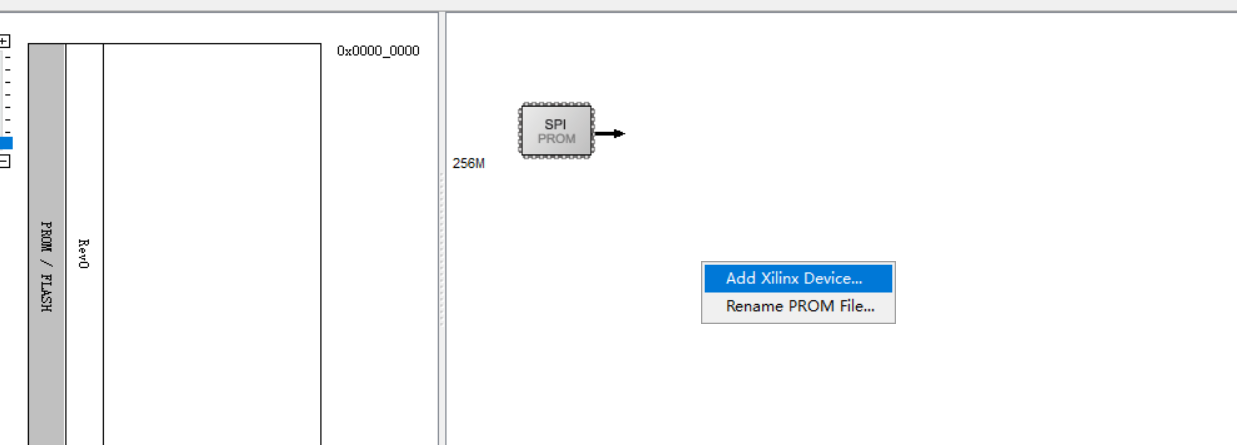
添加XILINX器件,添加固化所需要的bit文件,右键点击生成文件。
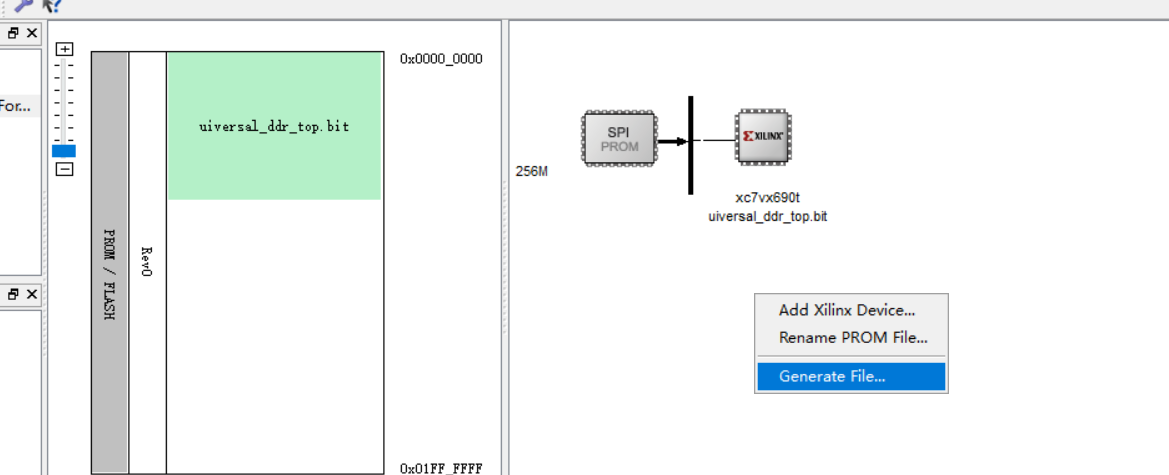
生成成功。
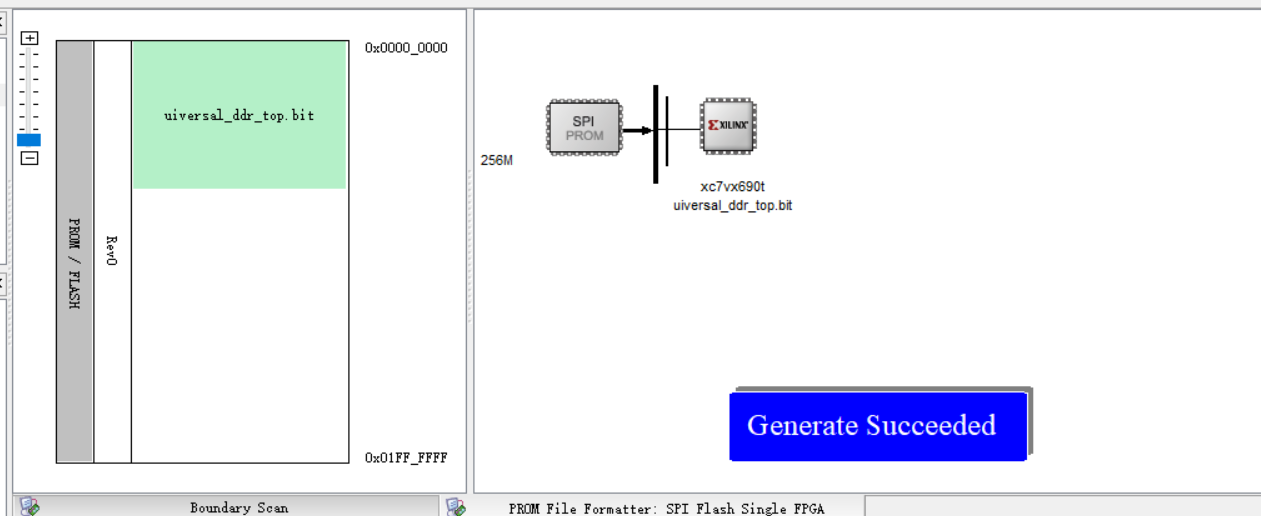
连接板卡后,选择初始化链路,添加xilinx器件,和固化的SPI或者BPI FLASH,操作步骤同ISE固化步骤。

选择下载固化的mcs文件,点击烧写固化。
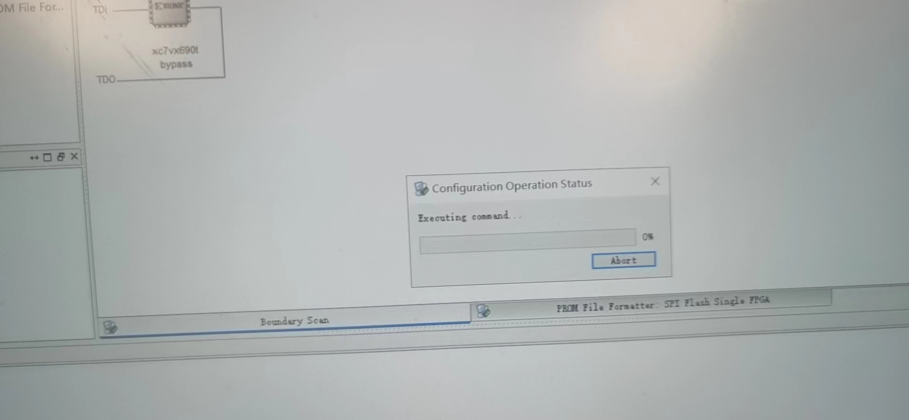
固化成功后应显示如下界面:
ZYNQ固化
ZYNQ固化参考提供的GD固化指导文件,将软件路径下的Uboot文件夹下的zynq_qspi_xx_xxxx.bin文件进行替换,本质应还是修改BIN文件后调过器件ID核查。

由于ZYNQ可以使用vivado进行固化,也可以使用SDK进行固化(高版本叫vitis,道理相同),所以根据使用软件替换掉相应的BIN文件,即可完成ZYNQ芯片的固化。
FSBL文件以及ZYNQ的镜像文件按正常步骤进行操作生成,无需进行额外修改。
找到软件安装路径,找到uboot文件夹,路径如下:
../../Xilinx/Vivado/2021.1/data/xicom/cfgmem/uboot
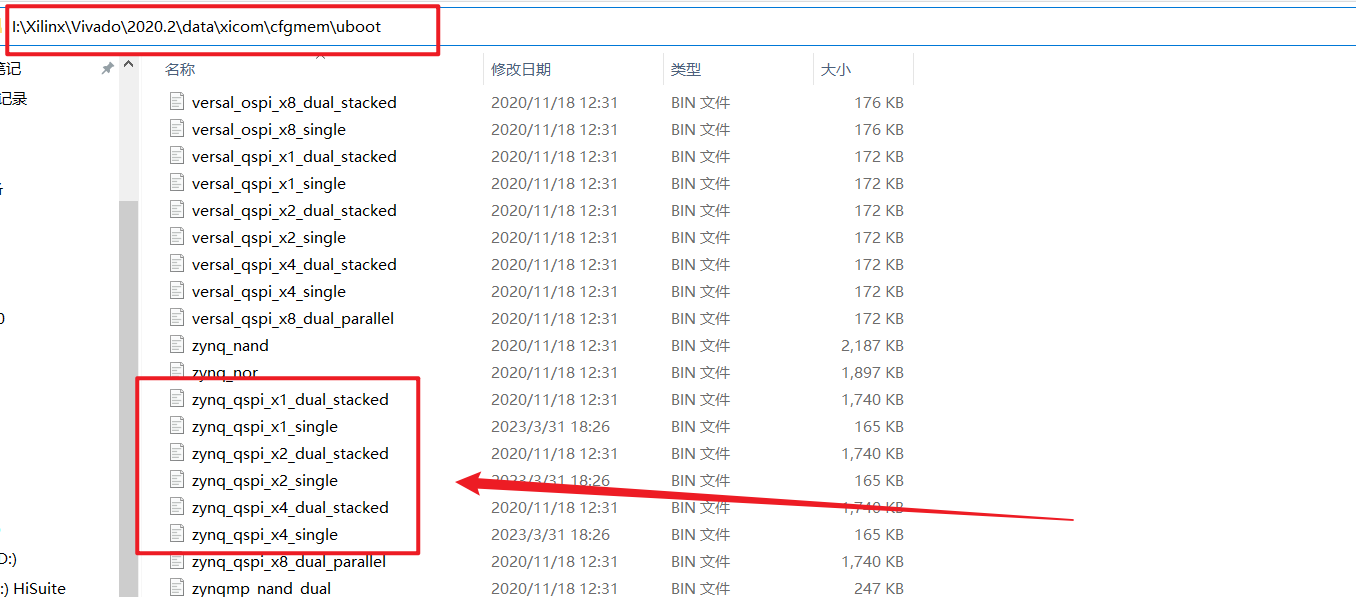
使用GD提供的qspi.bin文件替换掉软件自带的bin文件。
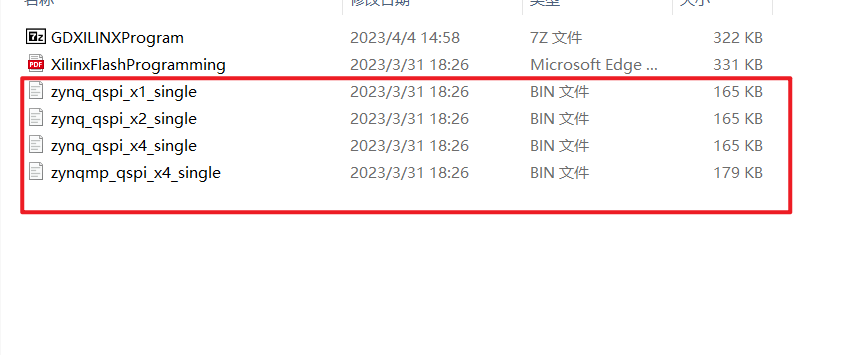
依据GD建议选择的MX型号的FLASH,选择相应容量的FLASH进行固化,即可。
如果使用SDK或者Vitis,选择相应版本的软件找到uboot路径,
Vitis路径如下:
../../Xilinx/Vitis/2021.1/data/xicom/cfgmem/uboot
SDK路径如下:
../../Xilinx/SDK/2018.3/data/xicom/cfgmem/uboot
完成替换后,使用SDK固化(vitis固化)操作同常规操作。
小结
GD系列FPGA和ZYNQ固化所需文件可私信交流获取。
相关文章:

GD(兆易创新)系列FLASH进行FPGA和ZYNQ配置固化相操作
写在前面 本文主要针对使用GD(兆易创新)系列的FLASH做启动配置片时,遇到的相关问题进行简单整理复盘,避免后人踩坑。 本人操作固化芯片型号为:ZYNQ7045、690T(复旦微替代型号V7 690T)。 7系列…...

通过一个小例子来看一下C语言指针 p、*p、p、*p、*p分别代表什么
前言 在C语言中,指针是非常重要的概念。指针是一个变量,其值为另一个变量的地址。使用指针可以直接访问内存中的数据,这使得C语言非常灵活和强大。在学习C语言时相比大家都已经知道了&和*的区别了,但是你知道*&p和&*…...

【内摹访谈】谈谈AI爆发前夜的B端设计
本文来自摹客产品设计团队(MPD)的设计专栏“内摹访谈”。专栏介绍:专栏名称来源于西方美学理论「内摹仿说」,意指审美活动与摹仿活动紧密相连,审美不只针对表象动作,其核心在于由物及我,从表观带…...

Redis—AOF持久化
一、AOF定义 保存写操作命令到日志的持久化方式,就是 Redis 里的 AOF(Append Only File) 持久化功能 定义:以日志的形式记录每个操作,记录写指令不记录读指令,只许追加⽂件不允许修改,AOF保存的是appendonly.aof⽂件…...
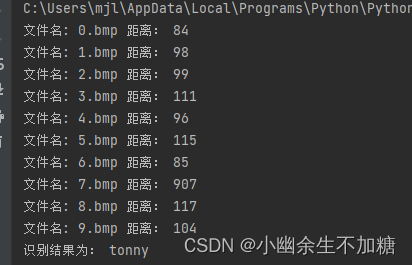
OpenCV实例(五)指纹识别
OpenCV实例(五)指纹识别 1.指纹识别概述1.1概述1.2原理 2.指纹识别算法2.1特征提取2.2MCC匹配方法2.3尺度不变特征变换(SIFT) 3.显示指纹的关键点4.基于SIFT的指纹识别 作者:Xiou 1.指纹识别概述 1.1概述 指纹识别&…...
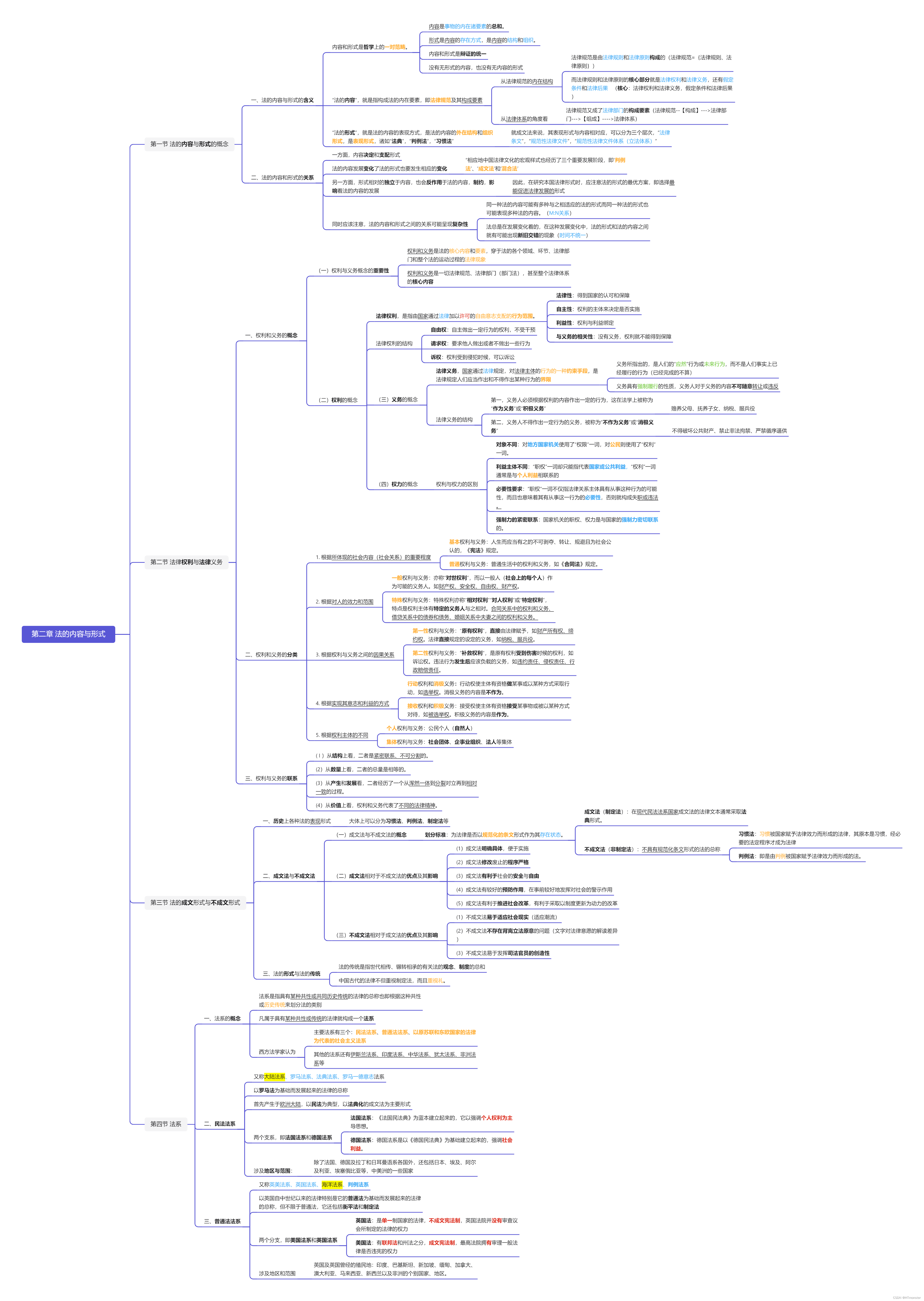
第二章 法的内容与形式
目录 第一节 法的内容与形式的概念 一、法的内容与形式的含义 二、法的内容和形式的关系 第二节 法律权利与法律义务 一、权利和义务的概念 二、权利和义务的分类 三、权利与义务的联系 第三节 法的成文形式与不成文形式 一、历史上各种法的表现形式 二、成文法与不成文…...

外包干了四年,感觉废了..
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
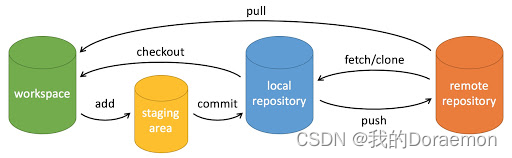
Git如何推送当前代码到远程仓库
第一种方法 (建立在已经配置好用户变量和ssh基础上) 在本地创建git仓库 git init 绑定远程仓库,origin是给远程仓库起的别名,也可以起其他名字,但是如果用origin,git push时可以不指出名字,如果…...

第五章 工厂模式
文章目录 一、简单工厂模式1、传统方式实现披萨订购( 可以忽略)披萨父类 Pizza子类胡椒披萨 PepperPizza子类印度披萨 GreekPizza订购披萨 OrderPizza订购披萨的 客户端 PizzaStore运行结果传统的方式的优缺点,新增子类需要修改的地方牵扯太多传统方式的究极耦合 2、…...
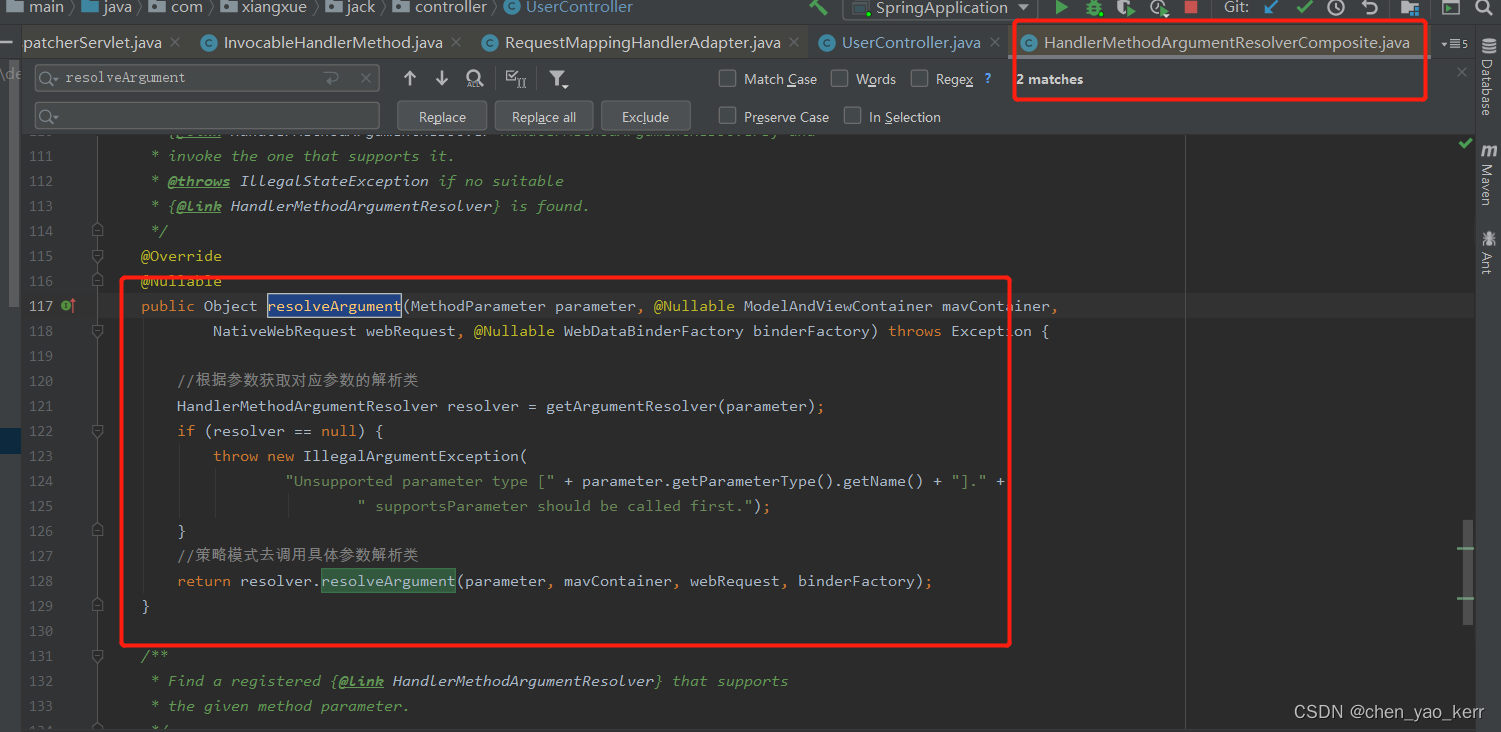
Spring MVC 参数解析(13)
目录 简介 调用流程 1. 首先,还是需要进行到前端控制器的doDispatch方法,这是我们的调用Spring MVC的核心入口方法 2. 在doDispatch方法内部,我们调用到了HandlerAdapter.handle(*****) 方法 3. 最终,我们会来到 RequestMappi…...

探索 Qt WebEngineWidgets:从底层原理到高级应用与技巧
探索 Qt WebEngineWidgets:从底层原理到高级应用与技巧 (Exploring Qt WebEngineWidgets: From Fundamentals to Advanced Applications and Techniques 一、Qt WebEngineWidgets 模块简介及原理 (Introduction and Principles of Qt WebEngineWidgets Module)1. Qt…...
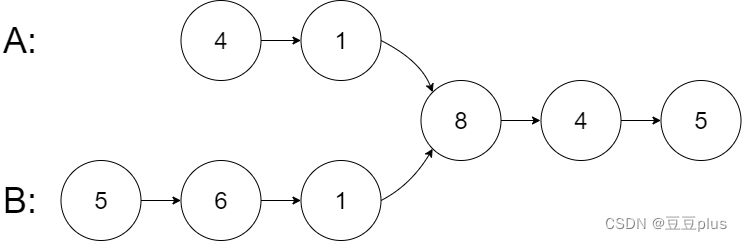
leetcode160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 图示两个链表在节点 c1 开始相交: 题目数据 保证 整个链式结构中不存在环。 注意,函数返回结果后&…...

核心业务7:放款实现
核心业务7:放款实现 1.放款实现流程 -------------------未完成生成借款人还款计划和投资人回款计划-------------- 2.数据库表 3.前端流程 4.汇付宝流程 5.尚融宝后端流程 -------------------未完成生成借款人还款计划和投资人回款计划-------------- -------------…...

STM32F4系列芯片RTC模块介绍
RTC是“实时时钟”的缩写,它是一种芯片,在计算机等电子产品中广泛应用。RTC提供了实时时钟计时功能和存储时间的能力,即时钟模块,常用于控制和记录时间的应用场合。 RTC的工作原理 RTC主要由时钟电路、电源管理电路、晶振电路、…...

MySQL 在线人数 场景分析
一般在直播或者游戏中经常会统计用户在线人数,主要分为求每个时刻的在线人数和求某个时刻的在线人数两种。 【场景】:某个时刻的在线人数、每个时刻的在线人数 【知识点】:窗口函数、时间函数、sum(tag) over (order by dt,tag desc rows b…...

使用mybatis和dynamic-datasource-spring-boot-starter动态切换数据源操作数据库
记录:415 场景:使用mybatis和dynamic-datasource-spring-boot-starter动态切换数据源操作数据库。 版本:JDK 1.8,Spring Boot 2.6.3,dynamic-datasource-spring-boot-starter-3.3.2,mybatis-3.5.9。 源码:https://github.com/b…...

【日常刷题】迷宫问题
描述 定义一个二维数组 N*M ,如 5 5 数组下所示: int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走…...

【Python童年游戏】满满的回忆杀—那些年玩过的童年游戏你还记得吗?那个才是你的菜?看到第一个我就泪奔了(致我们逝去的青春)
导语 滴一一学生卡🙌 结伴上车的学生仔子们 用笑声打破车厢的沉默 大人眼里的晚高峰 是给放学后快乐😀时光的加时 下车的学生匆匆起身带起 一阵熟悉的栀子香于💓 是关于校园的记忆 开始零零散散地闪现 放学后集合的秘密基地/跟着城…...

C++ | 认识标准库string和vector
本文概要 本篇文章主要介绍C的标准库类型string和vector,文中描述和代码示例很详细,看完即可掌握,感兴趣的小伙伴快来一起学习吧。 🌟🌟🌟个人简介 🌟🌟🌟 ☀️大家好&a…...
)
JAVA面试宝典: SpringCloud知识点(通俗易懂易背)
1、什么是 Spring Cloud? Spring Cloud 是基于 Spring Boot 的微服务架构开发工具箱,提供了在分布式系统中构建可靠的、弹性的、灵活的应用所需的大多数工具。Spring Cloud 中包含的子项目如下: Spring Cloud Config:配置管理工具…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
