NOIP模拟赛 T3区间
题目大意
有 n n n个数字,第 i i i个数字为 a i a_i ai。有 m m m次询问,每次给出 k i k_i ki个区间,每个区间表示第 l i , j l_{i,j} li,j到第 r i , j r_{i,j} ri,j个数字,求这些区间中一共出现了多少种不同的数字。部分数据强制在线。
时限1s,空间8MB。
输入格式
第一行包括三个整数 n , m , p n,m,p n,m,p, p p p为 0 0 0或 1 1 1表示是否强制在线。
第二行 n n n个正整数,第 i i i个表示 a i a_i ai。
接下来依次给出每个询问,每个询问第一行一个正整数,表示 k i k_i ki。接下来 k i k_i ki行,每行两个正整数,分别表示 l i , j l_{i,j} li,j和 r i , j r_{i,j} ri,j。
若 p = 1 p=1 p=1且这不是第一个询问,则输入的 l i , j l_{i,j} li,j和 r i , j r_{i,j} ri,j是经过加密的,你需要将这两个数字分别异或上上一个询问的答案,对 n n n取模后再加 1 1 1,两者的较小值为真实的 l i , j l_{i,j} li,j,较大值为真实的 r i , j r_{i,j} ri,j。
输出格式
对每个询问输出一行一个整数表示答案。
输入样例
3 2 0
1 2 1
1
1 2
2
1 1
3 3
输出样例
2
1
数据范围
1 ≤ n , m , ∑ k i , a i ≤ 1 0 5 , 1 ≤ l i , j ≤ r i , j ≤ n 1\leq n,m,\sum k_i,a_i\leq 10^5,1\leq l_{i,j}\leq r_{i,j}\leq n 1≤n,m,∑ki,ai≤105,1≤li,j≤ri,j≤n
题解
首先,我们考虑 p = 0 p=0 p=0的情况。
我们可以用 b i t s e t bitset bitset来维护每个点是否出现。先把各个区间离线下来,用莫队求出每个区间的 b i t s e t bitset bitset。把每个询问并起来。这样做的时间复杂度为 O ( n n + n m 64 ) O(n\sqrt n+\dfrac{nm}{64}) O(nn+64nm)。
空间开不下,我们考虑优化。
既然要用 b i t s e t bitset bitset,那么时间复杂度肯定是要带 n m 64 \dfrac{nm}{64} 64nm的了。我们不妨将每 n 64 \dfrac{n}{64} 64n个元素分一块,对于每次询问,非整块的暴力处理,再预处理整块到整块的 b i t s e t bitset bitset即可。
空间开不下,就对这 64 64 64个块建 S T ST ST表。建 S T ST ST表不用倍增,对每种长度从左到右推一遍即可。
在优化一下常数。只出现过一次的权值,把它们单独求一个前缀和,每次特殊处理即可。这样的话,每个权值至少出现两次,离散化之后权值个数能减少至少一半。
离散化的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),建 S T ST ST表的时间复杂度为 O ( n log 64 ) O(n\log 64) O(nlog64),查询的时间复杂度为 O ( n m 64 + 64 n ) O(\dfrac{nm}{64}+64n) O(64nm+64n),总时间复杂度为 O ( n m 64 ) O(\dfrac{nm}{64}) O(64nm)。因为权值个数减半,所以时间复杂度能降低到 O ( n m 128 ) O(\dfrac{nm}{128}) O(128nm)。
空间复杂度为 O ( n log 64 ) O(n\log 64) O(nlog64)。
这道题有一定的思维难度,可以结合代码帮助理解。
code
#include<bits/stdc++.h>
#define N 100032
#define K 1563
#define Z 782
using namespace std;
int n,m,p,c1=0,lst,ans,a[N+5],s[1<<16],t[105],c[N+5],sum[N+5];
struct pt{unsigned long long z[Z];void set(int x){z[x>>6]|=1ull<<(x&63);}void rev(int x){z[x>>6]^=1ull<<(x&63);}int count(){int re=0;for(int i=0;i<Z;i++){re+=s[z[i]>>48]+s[(z[i]>>32)&65535]+s[(z[i]>>16)&65535]+s[z[i]&65535];}return re;}
}v,b[6][70];//按颜色分成64块
struct node{int l,r;
}w[N+5];
bool cmp(node ax,node bx){if(ax.l!=bx.l) return ax.l<bx.l;return ax.r<bx.r;
}
void kuai(int l,int r){if(l>r) return;int x=t[r-l+1];for(int i=0;i<Z;i++){v.z[i]|=b[x][l].z[i]|b[x][r-(1<<x)+1].z[i];}
}//所有大块处理
void dd(int l,int r){if((l-1)/K==(r-1)/K){for(int i=l;i<=r;i++) v.set(a[i]);}else{for(int i=l;i<=(l-1)/K*K+K;i++) v.set(a[i]);kuai((l-1)/K+1,(r-1)/K-1);for(int i=(r-1)/K*K+1;i<=r;i++) v.set(a[i]);}
}//分块
int main()
{scanf("%d%d%d",&n,&m,&p);for(int i=2;i<=64;i++) t[i]=t[i>>1]+1;for(int i=1;i<1<<16;i++) s[i]=s[i>>1]+(i&1);for(int i=1;i<=n;i++){scanf("%d",&a[i]);++c[a[i]];}for(int i=1;i<=n;i++){sum[i]=sum[i-1];if(c[a[i]]==1){a[i]=0;++sum[i];}}//若只出现过一次,放到前缀和数组中for(int i=1;i<=n;i++){if(a[i]) c[++c1]=a[i];}sort(c+1,c+c1+1);c1=unique(c+1,c+c1+1)-c-1;for(int i=1;i<=n;i++){if(a[i]){a[i]=lower_bound(c+1,c+c1+1,a[i])-c;}}//离散化for(int i=0,x=K;i<6;i++,x<<=1){memset(v.z,0,sizeof(v.z));memset(c,0,sizeof(c));for(int j=1;j<=x;j++){if(!c[a[j]]) v.rev(a[j]);++c[a[j]];}b[i][0]=v;for(int j=K;j+x<=N;j+=K){for(int k=0;k<K;k++){if(!c[a[j+x-k]]) v.rev(a[j+x-k]);++c[a[j+x-k]];--c[a[j-k]];if(!c[a[j-k]]) v.rev(a[j-k]);}b[i][j/K]=v;}//按位置分成64块}//ST表for(int o=1,k,l,r;o<=m;o++){ans=0;memset(v.z,0,sizeof(v.z));scanf("%d",&k);for(int i=1;i<=k;i++){scanf("%d%d",&w[i].l,&w[i].r);if(p&&o>1){w[i].l=(w[i].l^lst)%n+1;w[i].r=(w[i].r^lst)%n+1;if(w[i].l>w[i].r) swap(w[i].l,w[i].r);}}sort(w+1,w+k+1,cmp);l=w[1].l;r=w[1].r;for(int i=2;i<=k;i++){if(w[i].l>r+1){ans+=sum[r]-sum[l-1];dd(l,r);l=w[i].l;}r=max(r,w[i].r);}ans+=sum[r]-sum[l-1];dd(l,r);//合并区间ans+=v.count()-(v.z[0]&1);//z[0]的第一个位置是为0的a值,不统计lst=ans;printf("%d\n",ans);//求答案}return 0;
}
相关文章:

NOIP模拟赛 T3区间
题目大意 有 n n n个数字,第 i i i个数字为 a i a_i ai。有 m m m次询问,每次给出 k i k_i ki个区间,每个区间表示第 l i , j l_{i,j} li,j到第 r i , j r_{i,j} ri,j个数字,求这些区间中一共出现了多少种不同的数字。部…...
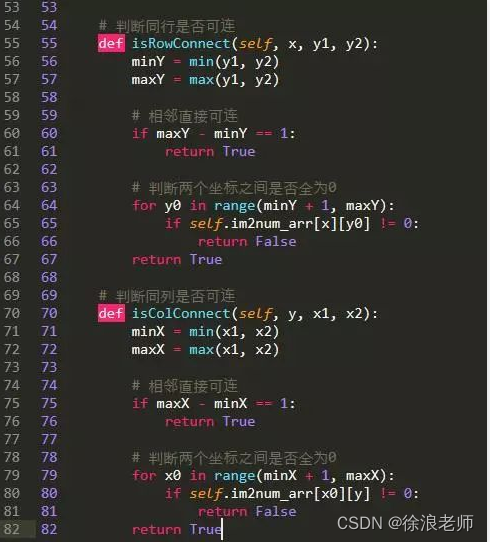
【Python】如何用pyth做游戏脚本(太简单了吧)
文章目录 前言一、开发前景二、开发流程3.1、获取窗口句柄,把窗口置顶3. 2、截取游戏界面,分割图标,图片比较 二、程序核心-图标连接算法(路径寻找)四、开发总结五、源码总结 前言 简述:本文将以4399小游戏…...
【Linux】磁盘与文件系统
目录 一、磁盘的物理结构 二、磁盘逻辑抽象 三、文件系统 1、Super Block 2、Group Descriptor Table 3、inode Table 4、Data Blocks 5、inode Bitmap 6、Block Bitmap 四、Linux下文件系统 1、inode与文件名 2、文件的增删查改 2.1、查看文件内容 2.2、删除文件…...
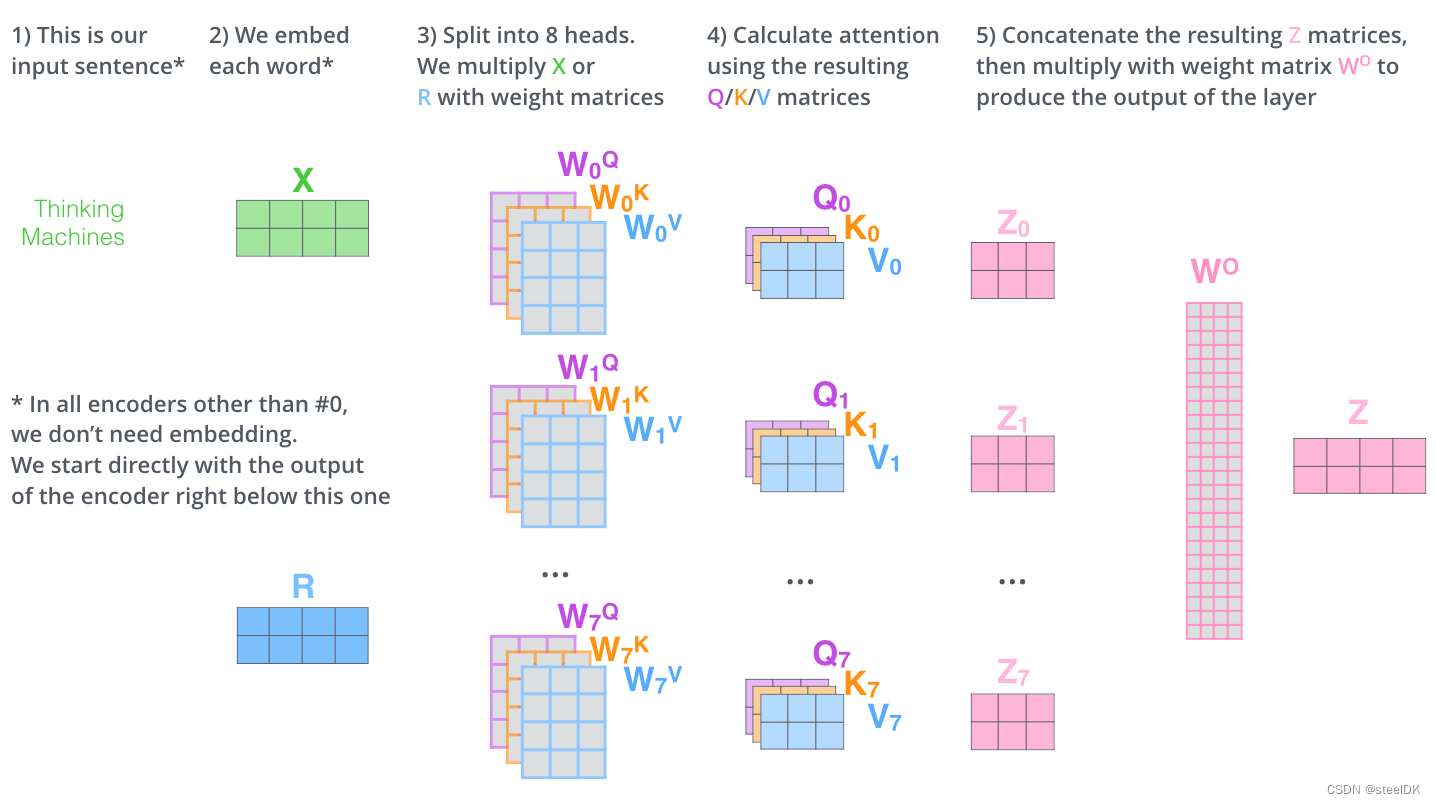
Transformer中的注意力机制及代码
文章目录 1、简介2、原理2.1 什么是注意力机制2.2 注意力机制在NLP中解决了什么问题2.3 注意力机制公式解读2.4 注意力机制计算过程 3、单头注意力机制与多头注意力机制4、代码4.1 代码14.2 代码2 1、简介 最近在学习transformer,首先学习了多头注意力机制…...

ChatGPT在连续追问下对多线程和双重检查锁模式的理解--已经超越中级程序员
一、问: private static final Map<Method, GZHttpClientResultModel> CACHE_RESULT_MODEL new ConcurrentHashMap<>();public void abc(Method method){cacheResultMode(method);GZHttpClientResultModel model CACHE_RESULT_MODEL.get(method);}pr…...

每天一道大厂SQL题【Day22】华泰证券真题实战(四)
每天一道大厂SQL题【Day22】华泰证券真题实战(四) 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题&…...
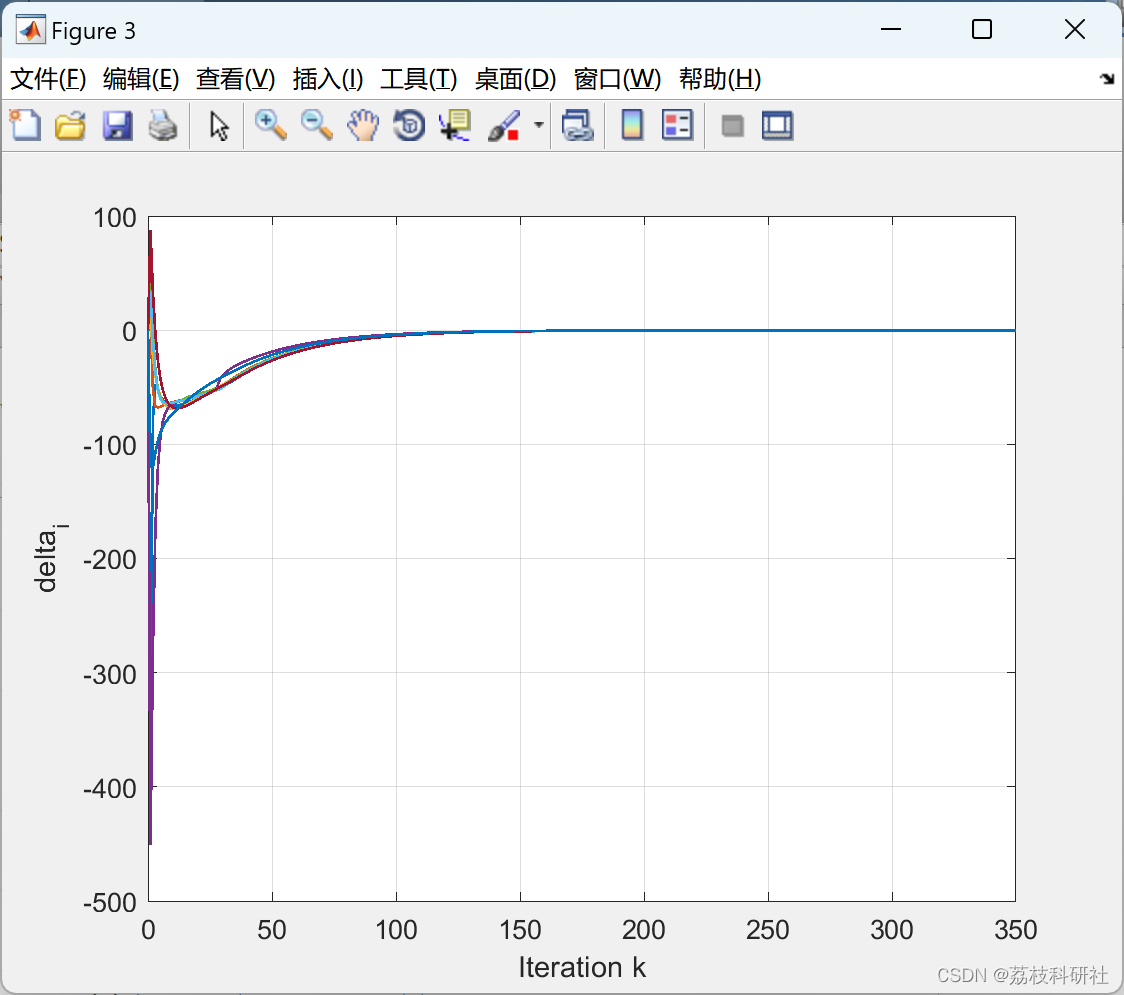
【智能电网】智能电网中针对DOS和FDIA的弹性分布式EMA(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

IDEA 创建微服务项目实例
🎈 作者:Linux猿 🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊! 🎈 关注专栏:C/C++面试通关【精讲】 优质好文持续更新中……🚀🚀🚀 🎈 欢迎小伙伴们点赞👍、收藏⭐、留…...

注册苹果开发者账号的方法
在2020年以前,注册苹果开发者账号后,就可以生成证书。 但2020年后,因为注册苹果开发者账号需要使用Apple Developer app注册开发者账号,所以需要缴费才能创建ios证书了。 所以新政策出来后,注册苹果开发者账号&#…...

OpenCV2 计算机视觉应用编程秘籍:1~5
原文:OpenCV2 Computer Vision Application Programming Cookbook 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线…...
Domino自带的JSON校验工具
大家好,才是真的好。 JSON数据在Notes/Domino已经变得非常重要。从Domino 10开始,在LotusScript语言中就加入了对JSON数据处理功能。在管理中,我们知道,从Domino 12版本开始就支持Domino自动化配置,也是使用JSON数据作…...
CentOS(linux)使用Docker安装nacos
1. 拉取nacos镜像 docker pull nacos/nacos-server:2.0.3 2. 创建所需文件夹(以安装在home目录下为例) 1) 创建conf文件夹 mkdir -p /home/nacos/conf a. 新增文件application.properties(或者不增加该文件,会使用默认的) 文件内容如下: # spring server.servlet.contextP…...

无线测温在线监测系统工作原理与产品选型
摘要:本文首先介绍了无线测温在线监测系统的基本工作原理以及软硬件组成,重点介绍了在线监测的无线测温技术特点。在此研究基础上,探讨了无线测温在线监测系统在实际工作场景中的应用案例,证明了其在温度检测方面的重要应用价值。…...
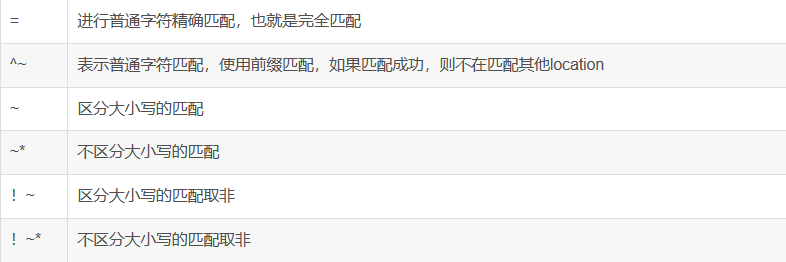
Nginx rewrite ——重写跳转
Nginx常见模块 http http块是Nginx服务器配置中的重要部分,代理、缓存和日志定义等绝大多数的功能和第三方模块的配置都可以放在这模块中。作用包括:文件引入、MIME-Type定义、日志自定义、是否使用sendfile传输文件、连接超时时间、单连接请求数上限等…...

【华为OD机试真题 C++】1038 - 全量和已占用字符集 | 机试题+算法思路+考点+代码解析
文章目录 一、题目🔸题目描述🔸输入输出🔸样例1二、代码参考作者:KJ.JK🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🍂个人博客首页: KJ.JK 💖系列专栏:华为OD机试真题(C++) 一、题目 🔸题目描述 所谓水仙花数,是指一个n位的正整数…...

网络中的网关和物联网的网关区别 局域网 路由器 交换机 服务器
网关:是个概念。连接两种不同的网络。例如局域网要与外部通信,需要经过网关。 设备和设备之间的通信,转换协议需要网关 路由器里有功能是对网关这个概念的实现。 所以网关它可以是路由器,交换机或者是PC。 路由器有网关功能&a…...

2023 年嵌入式世界的3 大趋势分析
目录 大家好,本文讲解了嵌入式发展的3个大趋势,分享给大家。 趋势#1 – Visual Studio Code Integration 趋势#2 –支持“现代”软件流程 趋势 #3 – 在设计中利用 AI 和 ML 结论 大家好,本文讲解了嵌入式发展的3个大趋势,分享…...

基于 DolphinDB 机器学习的出租车行程时间预测
DolphinDB 集高性能时序数据库与全面的分析功能为一体,可用于海量结构化数据的存储、查询、分析、实时计算等,在工业物联网场景中应用广泛。本文以纽约出租车行程时间预测为例,介绍如何使用 DolphinDB 训练机器学习模型,并进行实时…...

Python调用最小二乘法
文章目录 numpy实现scipy封装速度对比 所谓线性最小二乘法,可以理解为是解方程的延续,区别在于,当未知量远小于方程数的时候,将得到一个无解的问题。最小二乘法的实质,是保证误差最小的情况下对未知数进行赋值。 最小…...

15.数据表格.上
本节课我们来开始了解 Layui 的内置模块:table 数据表格。 一.基本使用 1. table 模块,通过异步加载数据来渲染表格来展现数据内容; <table id"table"></table> layui.use([table], () > { const table …...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
