【dp】最长递增子序列
文章目录
- 方法一:动态规划
- 方法二:贪心 + 二分查找
- 构造最长递增子序列

方法一:动态规划
- dp[i]:末尾元素为arr[i]的最长子序列的长度
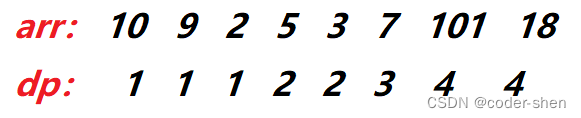
从0遍历到i - 1,若遍历到的元素小于当前值arr[i],表示当前值arr[i]可以和前面的某个值组成递增序列,则尝试更新dp[i]
int LIS(vector<int>& arr) {int n = arr.size();if(n == 0) return 0;vector<int> dp(n, 1);int ans = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(arr[j] < arr[i]){dp[i] = max(dp[i], dp[j] + 1);}}ans = max(ans, dp[i]);}return ans;
}
时间复杂度: O ( N 2 ) O(N^2) O(N2)
方法二:贪心 + 二分查找
我们考虑维护一个数组 min_tails,min_tails[i]表示长度为i + 1的递增子序列末尾元素的最小值,min_tails并不是记录arr中的递增子序列

看最后一个g数组,g[2]=3,表示长度为3的递增子序列末尾的最小值为3。长度为3的递增子序列有[1,6,7]、[1,2,4]、[1,2,5]、[1,2,3]
为什么min_tails数组中要维护各个不同长度递增子序列末尾元素的最小值呢?
min_tails数组中维护各个不同长度递增子序列末尾元素的最小值时,arr的后续元素可以和不同长度子序列末尾的最小值比较,从而确定后续元素可以加入哪个子序列,成为新的递增子序列

int LIS(vector<int>& arr) {int n = arr.size();if(n == 0) return 0;vector<int> tails(n);min_tails[0] = arr[0];int len = 1;for(int i = 1; i < n; i++){// 如果当前元素比长度为len的子序列末尾元素的最小值大,说明当前元素可以和长度为len的子序列组成新的递增子序列if(min_tails[len - 1] < arr[i]){min_tails[len] = arr[i];len++;continue;}// 二分:用arr[i]更新tails中最靠左侧的大于arr[i]的值int l = 0;int r = len;while(l < r){int mid = l + (r - l) / 2;if(min_tails[mid] < arr[i]) l = mid + 1; // 用l找第一个比arr[i]大的值,也可以找最后一个小于等于arr[i]的值else r = mid;}min_tails[l] = arr[i];}return len;
}
构造最长递增子序列
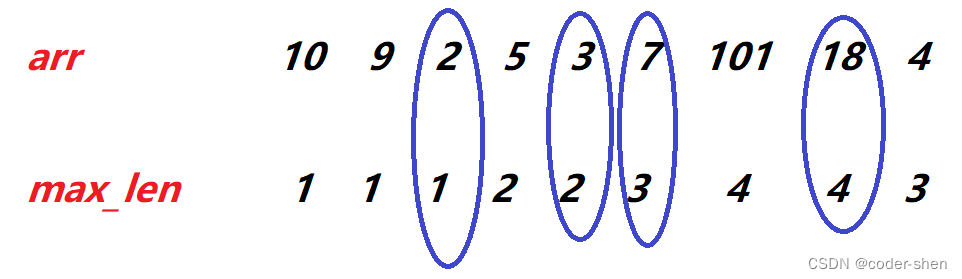
max_len相同时取最小的,ans初始化为len个元素,从后往前填写。如果max_len相同,靠后的arr[i]一定更小,若靠后的arr[i]更大,那max_len就不能相同了。比如:
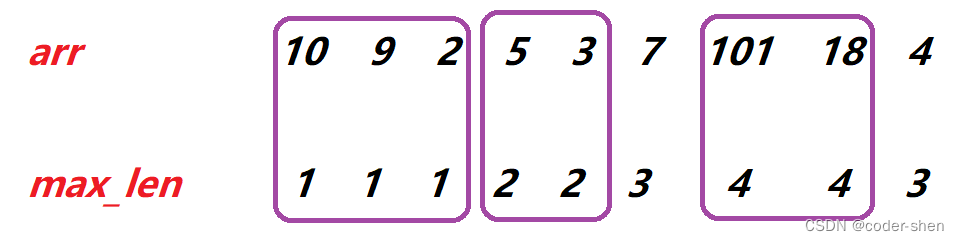
class Solution {
public:vector<int> LIS(vector<int>& arr) {int n = arr.size();if(n < 2) return arr;vector<int> min_tails(n); // min_tails[i]:长度为i+1的最长递增子序列末尾元素的最小值min_tails[0] = arr[0];int len = 1; // 当前最长递增子序列的长度vector<int> max_len(n); // max_len[i]:表示以arr[i]结尾的最长递增子序列的长度max_len[0] = 1;for(int i = 1; i < n; i++){// 当前元素arr[i]已经比当前最长递增子序列末尾元素的最小值要大,说明可以和当前递增子序列组成新的递增子序列if(arr[i] > min_tails[len - 1]){min_tails[len] = arr[i];max_len[i] = len + 1; // arr[i]可以增加最长递增子序列的长度len++;continue;}// arr[i]不能和当前最长递增子序列组成新的递增子序列,可以尝试用arr[i]和较短的递增子序列组成新的递增子序列(极端情况下,arr[i]自己组成长度为1的递增子序列)// 在[l, r)之间找第一个大于arr[i]的位置,说明arr[i]可以和前面较短的递增子序列组成新的递增子序列,用arr[i]更新第一个大于arr[i]的元素,即让某递增子序列的长度不变,而末尾元素变小int l = 0;int r = len;while(l < r){int mid = l + (r - l) / 2;if(min_tails[mid] < arr[i]) l = mid + 1;else r = mid; // 不能是r = mid - 1,因为要找第一个大于arr[i]的值,此时min_tails[mid] >= arr[i],r = mid - 1会跳过大于arr[i]的min_tails[mid]}min_tails[l] = arr[i];max_len[i] = l + 1; // arr[i]不能增加最长递增子序列的长度,min_tails[l]是第一个大于arr[i]的元素,即用arr[i]可以组成长度为l + 1的递增子序列}vector<int> ans(len);int idx = len - 1;// 只能按顺序填for(int i = n - 1; i >= 0; i--){// 遍历max_len数组,最大长度为idx + 1时才可填写ans[idx],max_len相同时必然取最靠后的arr[i],因为最靠后的最小if(max_len[i] == idx + 1){ans[idx] = arr[i];idx--;}}return ans;}
};
相关文章:

【dp】最长递增子序列
文章目录 方法一:动态规划方法二:贪心 二分查找构造最长递增子序列 方法一:动态规划 dp[i]:末尾元素为arr[i]的最长子序列的长度 从0遍历到i - 1,若遍历到的元素小于当前值arr[i],表示当前值arr[i]可以和…...

docker容器:Docker-Compose
目录 一、Docker-Compose 1、Docker-Compose使用场景 2、Docker-Compose简介 3、Docker-Compose安装部署 4、YML文件编写注意事项 5、Compose配置常用字段 6、 Docker Compose 常用命令 7、Docker Compose 文件结构 8、docker Compose撰写nginx 镜像 9、docker Compos…...

如何使用DNS实现融合CDN功能
将托管DNS解决方案与CDN配对可为您的网站提供额外的性能、可靠性和灵活性。 域名系统(DNS)是一种用于计算机、服务或连接到Internet或专用网络的任何资源的分层分布式命名系统,它将各种信息与分配给每个参与实体的域名相关联,它基…...
有关实现深拷贝的四种方法
深拷贝与浅拷贝: 在开始之前我们需要先了解一下什么是浅拷贝和深拷贝,其实深拷贝和浅拷贝都是针对的引用类型,JS中的变量类型分为值类型(基本类型)和引用类型;对值类型进行复制操作会对值进行一份拷贝,而对…...

Mysql 高可用部署实践
mysql主从是如何备份的? 在MySQL主从复制架构下,备份通常需要在主库和从库上分别进行。 主库备份: 在主库上进行备份时,可以使用mysqldump等命令生成SQL文件,并将其保存到本地或者远程服务器上。备份过程中需要注意以下几点&a…...

IEEE-TMI:张孝勇团队开发小鼠精细脑结构自动分割的深度学习算法
近日,复旦大学类脑智能科学与技术研究院青年研究员张孝勇课题组联合德国亥姆霍兹慕尼黑研究中心,在医学图像处理领域顶尖期刊《IEEE医学影像汇刊》(IEEE Transactions on Medical Imaging,TMI) 发表了题为《MouseGAN:用于小鼠大脑…...

八股文之面向对象和面向过程的区别
面向对象(Object-Oriented)和面向过程(Procedural)是两种不同的编程思想。 面向过程是以任务为中心,将程序分解成一系列步骤,在每个步骤中定义一个函数来完成特定的任务。它主要关注程序执行的过程和如何组…...

SpringBoot使用Redis实现分布式缓存
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
Three——二、加强对三维空间的认识
Three——二、加强对三维空间的认识 接上个例子我们接着往下看 辅助观察坐标系 THREE.AxesHelper()的参数表示坐标系坐标轴线段尺寸大小,你可以根据需要改变尺寸。 使用方法: // AxesHelper:辅助观察的坐标系 const axesHelper new THRE…...

【Java】Java8接口中方法区别和使用
Java接口说明 jdk1.8之前接口只能是抽象方法。实现接口必须重写所有方法,比较麻烦。在java8中,支持default和static方法,这样,实现接口时,可以选择是否对default修饰的方法重写。 抽象方法 接口当中的抽象方法&#x…...

WPF 控件库Live Charts 折线图多折线比较问题处理
使用Live Charts功能对比多条折线时当Label不是一一对应时会发现折线无法对比如 Labels List<double> list2 new List<double>(); list2.Add(2.1); //x为0.5时 list2.Add(2.2); //x为0.6时 …...
接口优化方案
前言 最近随着国产化热潮,公司的用于营业的电脑全部从windows更换成了某国产化电脑,换成国产化之后,我们系统的前台web界面也由之前的jsp页面重构成vue.所以之前的一体式架构也变成了前后端分离的架构。但是在更换过程后,发现一些…...

《商用密码应用与安全性评估》第二章政策法规2.1网络空间安全形式与商业密码工作
一、国际国内网络空间安全形势 网络空间已成为与陆地、海洋、天空、太空同等重要的人类第五空间。 1.国际形势 网络空间安全纳入国家战略 网络攻击在国家对抗中深度应用 网络空间已逐步深入网络底层固件 2.国内形势 核心技术仍受制于人 信息产品存在巨大安全隐患 关…...

C#实现将文件、文件夹压缩为压缩包
C#实现将文件、文件夹压缩为压缩包 一、C#实现将文件、文件夹压缩为压缩包核心 1、介绍 Title:“基础工具” 项目(压缩包帮助类) Description步骤描述: 1、创建 zip 存档,该文档包含指定目录的文件和子目录…...

程序员跳槽,要求涨薪50%过分吗?
如果问在TI行业涨工资最快的方式是什么? 回答最多的一定是:跳槽! 前段时间,知乎上这样一条帖子引发了不少IT圈子的朋友的讨论 ,有网友提问 “程序员跳槽要求涨薪50%过分吗?” 截图来源于知乎,…...
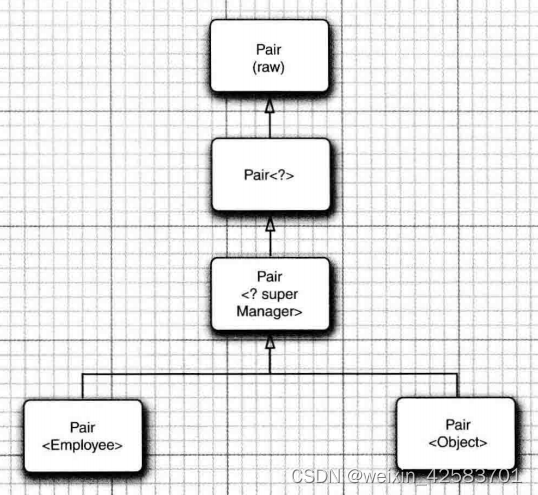
Java核心技术 卷1-总结-10
Java核心技术 卷1-总结-10 通配符类型通配符概念通配符的超类型限定无限定通配符通配符捕获 通配符类型 通配符概念 通配符类型中,允许类型参数变化。 例如,通配符类型Pair<? extends Employee>表示任何泛型Pair类型,它的类型参数是…...

React Props
state 和 props 主要的区别在于 props 是不可变的,而 state 可以根据与用户交互来改变。 所以,有些容器组件需要定义 state 来更新和修改数据。 而子组件只能通过 props 来传递数据。 props 使用 Demo.js : import React from reactfunct…...
【Hello Network】协议
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:简单介绍下协议并且设计一个简单的网络服务器 协议 协议的概念结构化数据传输序列化和反序列化网络版计算机服务端代码协议定制客户端代码服务线程执…...

零项目零科研,本科排名倒数,一战上岸上海交大电子与通信工程
笔者来自通信考研小马哥23上交819全程班学员 本科就读于哈工大(威海),本科成绩很差,专业排名62/99,没有科研,没有实验室,没有项目,连最基本大家都会参加的科技立项我四年也没有参与…...

NOIP模拟赛 T3区间
题目大意 有 n n n个数字,第 i i i个数字为 a i a_i ai。有 m m m次询问,每次给出 k i k_i ki个区间,每个区间表示第 l i , j l_{i,j} li,j到第 r i , j r_{i,j} ri,j个数字,求这些区间中一共出现了多少种不同的数字。部…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
