【Chatgpt4 教学】 NLP(自然语言处理)第九课 朴素贝叶斯分类器的工作原理 机器学习算法
我在起,点更新NLP自然语言处理==》《王老师带我成为救世主》
为啥为它单独开章,因为它值得,它成功的让我断了一更,让我实践了自上而下找能够理解的知识点,然后自下而上的学习给自己的知识升级,将自己提升到能够解决当前遇到的问题的水平。
(1)---------------------------------------------------------------------------------------
我:详细讲解朴素贝叶斯分类器的工作原理
AI:
朴素贝叶斯分类器(Naive Bayes Classifier)是一种基于贝叶斯定理和特征独立性假设的分类算法。它被广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。下面详细讲解朴素贝叶斯分类器的工作原理。
假设有一个包含N个文档的训练集,每个文档都属于一个类别。朴素贝叶斯分类器的目标是根据这个训练集,对新的文档进行分类。
1、特征提取
首先,需要将文档转换为特征向量。常见的方法是采用词袋模型,将每个文档表示为一个向量,向量中的每个元素表示一个词汇在该文档中出现的频率或者权重。
2、计算类别的先验概率
对于训练集中的每个类别c,计算该类别在训练集中的出现概率P(c),即P(c) = n_c / N,其中n_c表示属于类别c的文档数,N表示训练集中的文档总数。
3、计算特征的条件概率
对于每个类别c和每个特征f,计算在该类别下该特征的条件概率P(f|c),即在已知文档属于类别c的情况下,特征f出现的概率。
通常,采用朴素贝叶斯假设,即假设各个特征之间相互独立。根据该假设,可以将P(f|c)表示为各个特征独立事件的乘积:
P(f_1,f_2,...,f_n|c) = P(f_1|c) * P(f_2|c) * ... * P(f_n|c)
对于每个特征f,可以根据训练集中该特征在类别c中出现的频率计算P(f|c)。
4、计算后验概率
对于一个新的文档d,通过特征提取得到特征向量f(d),利用贝叶斯定理计算其属于类别c的后验概率P(c|f(d)):
P(c|f(d)) = P(f(d)|c) * P(c) / P(f(d))
其中,P(f(d)|c)是在类别c下,特征向量f(d)的条件概率,由于各个特征独立,可以表示为各个特征条件概率的乘积:
P(f(d)|c) = P(f_1(d)|c) * P(f_2(d)|c) * ... * P(f_n(d)|c)
P(f(d))是特征向量f(d)的先验概率,可以表示为所有类别的先验概率和条件概率之和:
P(f(d)) = ΣP(f(d)|c_i) * P(c_i)
最终,将文档d分类为具有最大后验概率的类别,即:
argmax P(c|f(d))
其中,argmax表示取得最大值的类别。
综上所述,朴素贝叶斯分类器的工作原理是,通过计算各个类别的先验概率和特征的条件概率,利用贝叶斯定理计算新文档属于各个类别的后验概率,最终将文档分类为具有最大后验概率的类别。由于朴素贝叶斯分类器假设各个特征之间相互独立,计算量较小,分类效果较好,被广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。
(2)---------------------------------------------------------------------------------------
我:朴素贝叶斯分类器的需不需要提供已经明确的分类标准集合?
AI:
是的,朴素贝叶斯分类器需要提供已经明确的分类标准集合,通常称为训练集。
在训练过程中,朴素贝叶斯分类器会利用训练集计算各个类别的先验概率和特征的条件概率,从而构建分类模型。
在测试时,朴素贝叶斯分类器会利用分类模型对新文档进行分类。
训练集通常由多个已经明确分类的文档组成,每个文档都被标注了对应的类别。在训练过程中,朴素贝叶斯分类器会利用这些文档计算各个类别的先验概率和特征的条件概率。
具体来说,对于每个类别,朴素贝叶斯分类器会统计训练集中该类别的文档数和各个特征在该类别下出现的频率,然后利用贝叶斯定理计算条件概率。
在测试时,朴素贝叶斯分类器会利用分类模型,计算新文档属于各个类别的后验概率,最终将文档分类为具有最大后验概率的类别。
因此,训练集是朴素贝叶斯分类器必不可少的一部分,它提供了分类器所需的先验概率和条件概率计算所需的信息。
在实际应用中,训练集的质量和规模对朴素贝叶斯分类器的分类效果影响很大,通常需要采用合适的数据预处理和特征选择方法,优化训练集的质量和规模,从而提高分类器的准确率和效率。
(3)---------------------------------------------------------------------------------------
我:
朴素贝叶斯分类器原理上面讲解的计算类别的先验概率部分, 训练集的类别的先验概率是不是都相等,因为假设了每个文档都属于一个类别
AI:
是的,由于朴素贝叶斯分类器假设每个文档都属于一个类别,因此训练集的类别的先验概率通常都是相等的。
在朴素贝叶斯分类器的计算过程中,会计算每个类别在训练集中出现的概率,即P(c),其中c表示类别。
由于训练集中的文档都被明确分类,因此对于每个文档,其属于某个类别的概率为1,属于其他类别的概率为0,因此所有类别在训练集中出现的概率都相等,即P(c) = 1/k,其中k表示类别的总数。
在实际应用中,如果训练集中某些类别的文档数量远远大于其他类别的文档数量,也可以通过调整先验概率,以反映实际情况。
例如,可以根据不同类别的文档数量,调整各个类别的先验概率,使其更准确地反映训练集中不同类别的分布情况,从而提高分类器的准确率和效率。
需要注意的是,如果训练集中存在未知的类别,例如新的文档属于之前未出现过的类别,那么朴素贝叶斯分类器的分类效果会受到影响,因为无法计算未知类别的先验概率。
因此,在实际应用中,需要保证训练集中覆盖了所有可能出现的类别,从而提高分类器的泛化能力和适用性。
(4)---------------------------------------------------------------------------------------
我:上面的“计算特征的条件概率”提到的特征f是指特征向量吗?
AI:
是的,上面提到的“计算特征的条件概率”中的特征f指的是文档的特征向量,其中每个特征表示一个词汇在文档中出现的频率或者权重。
特征向量是将文档表示为向量的一种方法,通过统计文档中各个词汇的出现频率或权重,将文档转换为一个高维向量。
在朴素贝叶斯分类器中,特征向量中的每个元素都表示一个特征,特征的条件概率指的是在已知文档属于某个类别的情况下,该特征在该类别中出现的概率。
例如,假设训练集中有1000篇文档,其中500篇属于类别A,500篇属于类别B,特征向量中的每个元素表示一个词汇在文档中出现的频率或权重,特征的条件概率指的是在已知文档属于类别A或B的情况下,该词汇在类别A或B中出现的概率。
(5)---------------------------------------------------------------------------------------
我:所以计算特征的条件概率是每个特征出现在已经类别的概率的乘积?
AI:
是的,计算特征的条件概率是指在已知文档属于某个类别的情况下,该类别下特征出现的概率,可以用各个特征条件概率的乘积来表示。
在朴素贝叶斯分类器中,特征的条件概率是指在已知文档属于某个类别c的情况下,特征f在该类别下出现的概率P(f|c),它可以通过在训练集中统计特征f在属于类别c的文档中出现的频率,再除以属于类别c的文档总数来估计。
假设特征向量f包含n个特征,那么在朴素贝叶斯分类器中,特征f出现的条件概率可以表示为各个特征条件概率的乘积:
P(f|c) = P(f_1|c) * P(f_2|c) * ... * P(f_n|c)
其中,P(f_i|c)表示在已知文档属于类别c的情况下,第i个特征f_i出现的概率。
需要注意的是,在朴素贝叶斯分类器中,特征之间相互独立的假设可能并不符合实际情况,因此在某些场景下,使用其他分类算法可能会得到更好的结果。
(6)---------------------------------------------------------------------------------------
我:如果当前特征未出现在这个类别岂不是乘积为0?
AI:
是的,如果某个特征在某个类别下从未出现过,那么按照上面的方式计算特征条件概率时,该特征的概率为0,最终得到的条件概率乘积也为0,这可能会导致朴素贝叶斯分类器的分类效果受到影响。
为了解决这个问题,通常会采用平滑技术,对特征出现的概率进行平滑,从而避免出现概率为0的情况。
其中最常用的平滑技术是拉普拉斯平滑(Laplace smoothing),也称为加1平滑,它将特征的出现次数加1,将类别下的特征总数加上词汇表的大小,从而保证了每个特征在每个类别下的概率都不为0。
具体来说,假设训练集中属于类别c的文档总数为N_c,词汇表的大小为V,特征f在属于类别c的文档中出现的次数为N_cf,那么在朴素贝叶斯分类器中,特征f出现的条件概率可以通过拉普拉斯平滑来计算:
P(f|c) = (N_cf + 1) / (N_c + V)
在使用拉普拉斯平滑后,每个特征在每个类别下的概率都不为0,从而避免了朴素贝叶斯分类器因概率为0而无法进行分类的问题。
(7)---------------------------------------------------------------------------------------
我:就是一旦有类别没包含该特征,所有类别内特征频率计数+1对么?
AI:
不完全是这样。
拉普拉斯平滑是为了避免特征在某个类别下从未出现过,导致条件概率为0的问题。
具体来说,拉普拉斯平滑是在估计条件概率时,在每个计数上都加上一个常数k,从而防止概率为0。
通常情况下,这个常数k取值为1,因为加1平滑是最常用的平滑技术之一。
具体来说,如果一个特征在训练集中从未出现在某个类别中,那么在计算条件概率时,直接将该特征的条件概率设为0是不合适的,因为这样会使得整个条件概率为0。
为了避免这种情况,拉普拉斯平滑会对特征的计数加上一个常数k,通常取值为1。
这样,在计算条件概率时,分子分母都会加上k,从而保证了特征的条件概率不为0。
具体来说,假设训练集中属于类别c的文档总数为N_c,词汇表的大小为V,特征f在属于类别c的文档中出现的次数为N_cf,那么在朴素贝叶斯分类器中,特征f出现的条件概率可以通过拉普拉斯平滑来计算:
P(f|c) = (N_cf + k) / (N_c + kV)
其中,k为常数,通常取值为1。
这样,在特征未出现在某个类别中时,计算出来的条件概率不会为0,而是一个很小的数值。
这种方式可以有效地避免概率为0的问题,并提高朴素贝叶斯分类器的分类效果。
---------------------------------------------------------------------------------------
至此,朴素贝叶斯分类器的工作原理我才全部理解,有疑问就要不断的问,希望与君共勉!
相关文章:
第九课 朴素贝叶斯分类器的工作原理 机器学习算法)
【Chatgpt4 教学】 NLP(自然语言处理)第九课 朴素贝叶斯分类器的工作原理 机器学习算法
我在起,点更新NLP自然语言处理》《王老师带我成为救世主》 为啥为它单独开章,因为它值得,它成功的让我断了一更,让我实践了自上而下找能够理解的知识点,然后自下而上的学习给自己的知识升级,将自己提升到能…...

基于html+css的图片展示17
准备项目 项目开发工具 Visual Studio Code 1.44.2 版本: 1.44.2 提交: ff915844119ce9485abfe8aa9076ec76b5300ddd 日期: 2020-04-16T16:36:23.138Z Electron: 7.1.11 Chrome: 78.0.3904.130 Node.js: 12.8.1 V8: 7.8.279.23-electron.0 OS: Windows_NT x64 10.0.19044 项目…...
Jupyter Notebook小知识
目录 1 快捷键1.1 常用快捷键1.2 魔法函数 2 常用快捷键2.1 模式切换2.2 命令模式快捷键2.3 编辑模式快捷键3 Matplotlib绘图 4 小技巧4.1 文件默认目录的查看以及更改4.2 更改主题颜色 5 其它5.1 python中 r, b, u, f 的含义5.2 f/format():格式化操作 6 常见问题6.1 查看模块…...
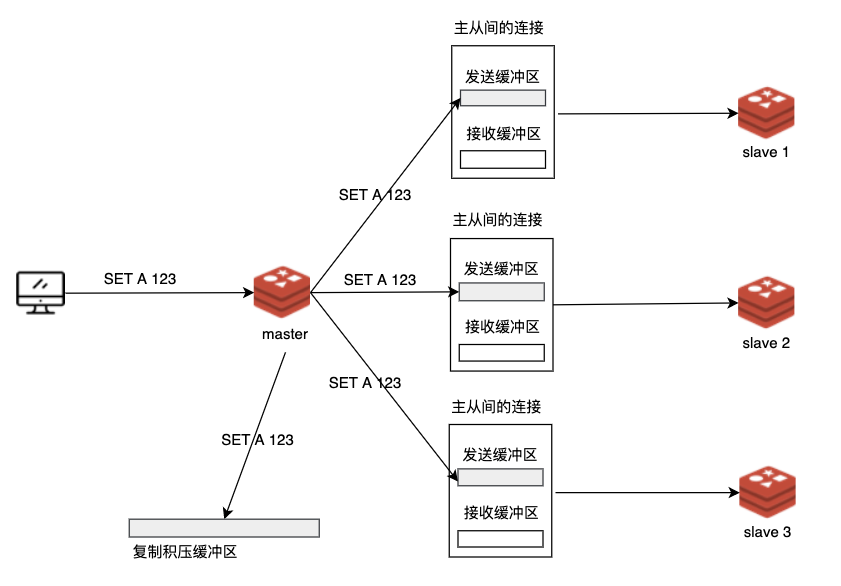
redis原理及进化之路
Redis 的主从复制经历了多次演进,本文将从最基本的原理和实现讲起,并层层递进,逐步呈现 Redis 主从复制的演进历史。大家将了解到 Redis 主从复制的原理,以及各个改进版本解决了什么问题,并最终看清 Redis 7.0 主从复制…...
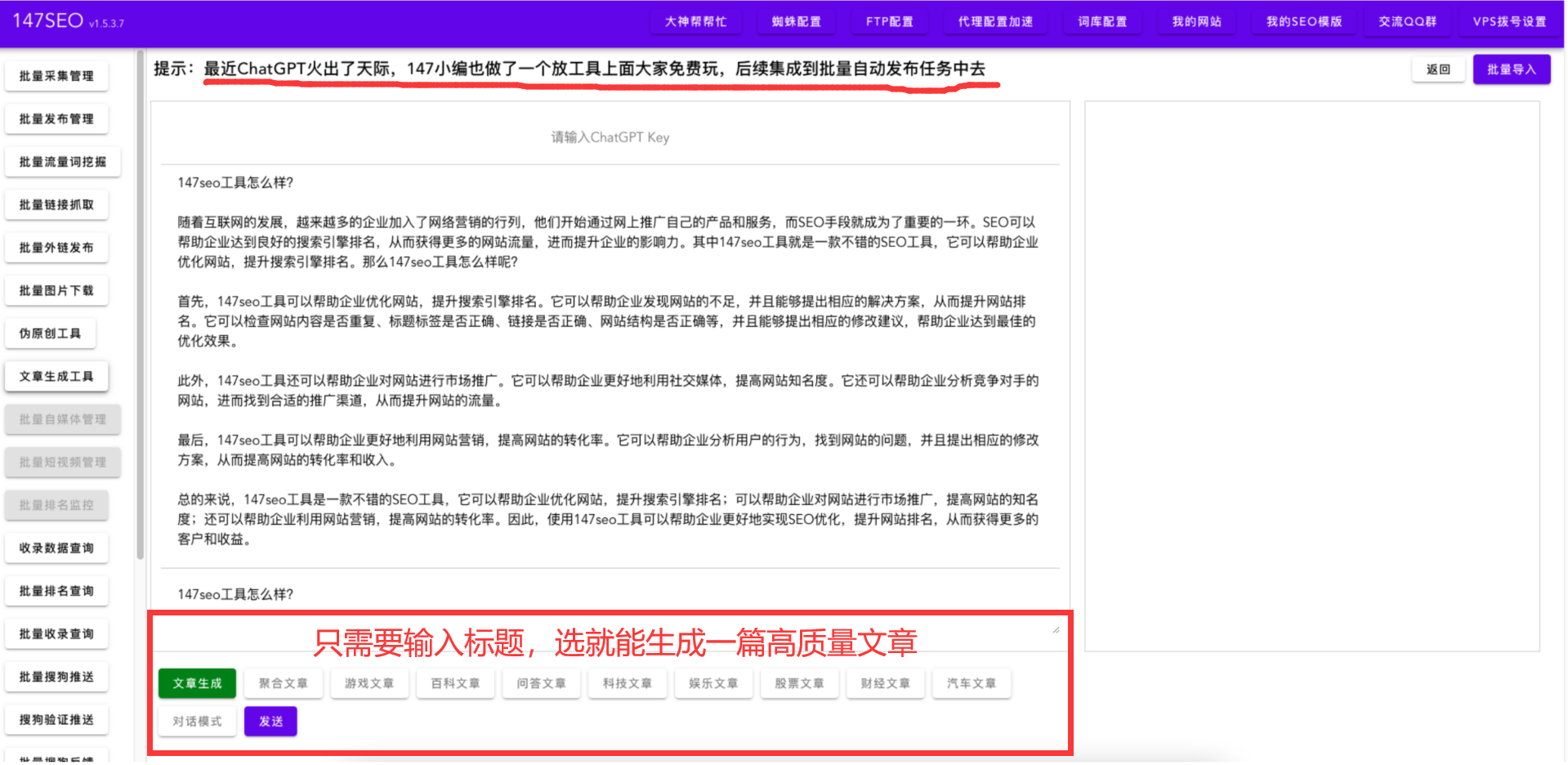
ai智能写作助手-ai自动写作软件
为什么要用ai智能写作工具 在数字化时代,AI(人工智能)技术已经被广泛应用于各种领域,其中之一是写作。AI智能写作工具是利用自然语言处理技术和机器学习算法来生成高质量的文章、博客、新闻稿等。这些工具不仅提供了便捷、高效的…...

redis持久化
redis提供两种方式进行持久化,一种是RDB持久化(原理是将Reids在内存中的数据库记录定时dump到磁盘上的RDB持久化),另外一种是AOF持久化(原理是将Reids的操作日志以追加的方式写入文件)。那么这两种持久化方…...
Vue项目基于driverjs实现新用户导航
引导页就是当用户第一次或者手动进行触发的时候,提示给用户当前系统的模块介绍,比如哪里是退出,哪里是菜单等等相应的操作。 无论是开发 APP 还是 web 应用,新手引导都是一个很常见的需求,一般在这2个方面需要新手引导…...
自编码器简单介绍—使用PyTorch库实现一个简单的自编码器,并使用MNIST数据集进行训练和测试
文章目录 自编码器简单介绍什么是自编码器?自动编码器和卷积神经网络的区别?如何构建一个自编码器?如何训练自编码器?如何使用自编码器进行图像压缩?总结使用PyTorch构建简单的自动编码器第一步:导入库和数…...
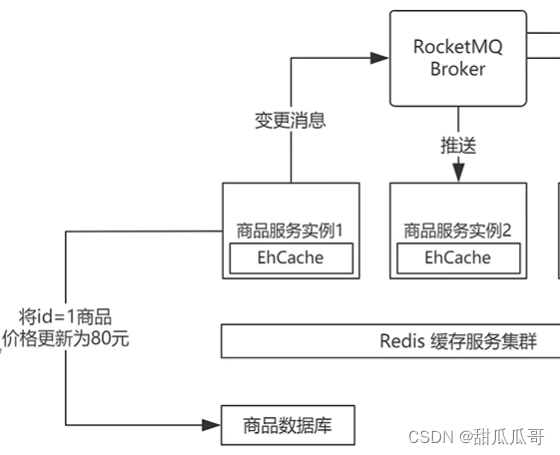
redis单机最大并发量
redis单机最大并发量 布隆过滤器多级缓存客户端缓存应用层缓存Expires和Cache-Control的区别Nginx缓存管理 服务层缓存进程内缓存进程外缓存 缓存数据一致性问题的解决引入多级缓存设计的时刻 Redis的速度非常的快,单机的Redis就可以⽀撑 每秒十几万的并发,相对于MySQL来说,性…...
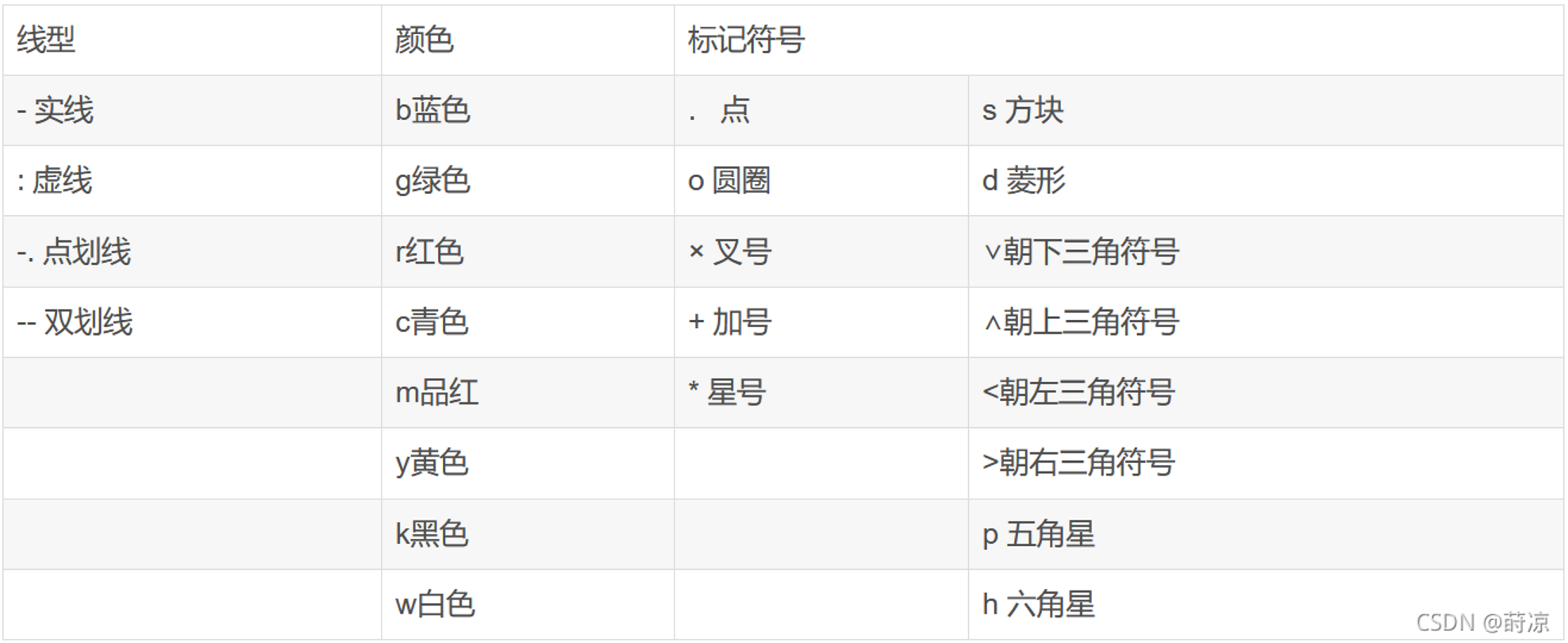
MTLAB绘图
这里写目录标题 一、图例1、散点图 二、绘图1、总体图形参数2、坐标、图框、网格图框去上右边框小刻度网格坐标范围和刻度控制旋转 坐标、刻度 3、图例图例位置和方向 Location和Orientation图例加标题 、分多列 4、文本 字、字体、字号5、线型 符号6、颜色栏 colorbar7、颜色8…...

自媒体必备素材库,免费、商用,赶紧马住~
自媒体经常需要用到各类素材,本期就给大家安利6个自媒体必备的素材网站,免费、付费、商用都有,建议收藏起来~ 1、菜鸟图库 https://www.sucai999.com/video.html?vNTYwNDUx 菜鸟图库可以找到设计、办公、图片、视频、音频等各种素材。视频素…...

ESP32设备驱动-BMP388气压传感器驱动
BMP388气压传感器驱动 文章目录 BMP388气压传感器驱动1、BMP388介绍2、硬件准备3、软件准备4、驱动实现1、BMP388介绍 BMP388 是一款非常小巧、低功耗和低噪声的 24 位绝对气压传感器。 它可以实现精确的高度跟踪,特别适合无人机应用。 BMP388 在 0-65C 之间的同类最佳 TCO,…...
攻防世界-Reversing-x64Elf-100
Reversing-x64Elf-100 18最佳Writeup由 yuchouxuan 提供 收藏 反馈 难度:1 方向:Reverse 题解数:15 解出人数:2460 题目来源: 题目描述: 暂无 note:undefined8 FUN_004006fd(long param_1){int local_2c;char *local_28 …...

C/C++每日一练(20230419)
目录 1. 插入区间 🌟🌟🌟 2. 单词拆分 🌟🌟 3. 不同路径 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日…...
[自注意力神经网络]Mask Transfiner网络-论文解读
本文为CVPR2022的论文。国际惯例,先贴出原文和源码: 原论文地址https://arxiv.org/pdf/2111.13673.pdf源码地址https://github.com/SysCV/transfiner 一、概述 传统的Two-Stage网络,如Mask R-CNN虽然在实例分割上取得了较好的效果ÿ…...

漫画:是喜,还是悲?AI竟帮我们把Office破活干完了
图文原创:亲爱的数据 国产大模型烈火制造。阿里百度字节美团各科技大佬不等闲。 大模型嘛,重大工程,对我等“怀保小民”来说,只关心怎么用,不关心怎么造。 我来介绍一下自己,我是一个写稿男团组合的成员&am…...

ChatGPT的原理分析
1.前言 ChatGPT是一种基于自然语言处理和人工智能技术的聊天机器人,它的基础是由OpenAI研发的GPT模型,其中GPT是Generative Pre-trained Transformer的缩写。GPT模型的训练使用了海量的语料库,可以预测下一个单词、短语、句子或文本…...
在线免费把Markdown格式文件转换为PDF格式
用CSDN的MarkDown编辑器在线转换 CSDN的MarkDown编辑器说实话还是挺好用的。 导出PDF操作步骤,图文配合看: 在MD编辑模式下写好MarkDown文章或者直接把要转换的MarkDown贴进来; 使用预览模式,然后在预览文件上右键选择打印&…...

R7-5 列车厢调度
R7-5 列车厢调度 分数 25 全屏浏览题目 切换布局 作者 周强 单位 青岛大学 1 <--移动方向/3 \2 -->移动方向 大家或许在某些数据结构教材上见到过“列车厢调度问题”(当然没见过也不要紧)。今天,我们就来实际操作一下列车…...
English Learning - L2 第 16 次小组纠音 弱读和语调 2023.4.22 周六
English Learning - L2 第 16 次小组纠音 弱读和语调 2023.4.22 周六 共性问题help /help/ 中的 e 和 lsorry /ˈsɒri/ 中的 ɒ 和 ilook out /lʊk aʊt/ 中的 ɒ 和 aʊdont /dəʊnt/ 中的 əʊemergency /ɪˈmɜːʤənsɪ/ 中的 ɜːname /neɪm/ 中的 eɪright /raɪt/…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
