DeepSORT中的卡尔曼滤波
本文是看了DeepSORT方法视频之后,关于其中使用的卡尔曼滤波的理解
DeepSORT视频链接
首先贴几个比较好的,与本文由有关的几个帖子
图说卡尔曼滤波,一份通俗易懂的教程
卡尔曼滤波(Kalman Filter)原理与公式推导
卡尔曼滤波:从入门到精通
协方差的计算:X,Y是随机变量,A,B是常数矩阵,如何证明cov(AX,BY)=Acov(X,Y)B’?
协方差的计算方法
矩阵求导
两个高斯分布乘积的理论推导
首先是视频中的一张图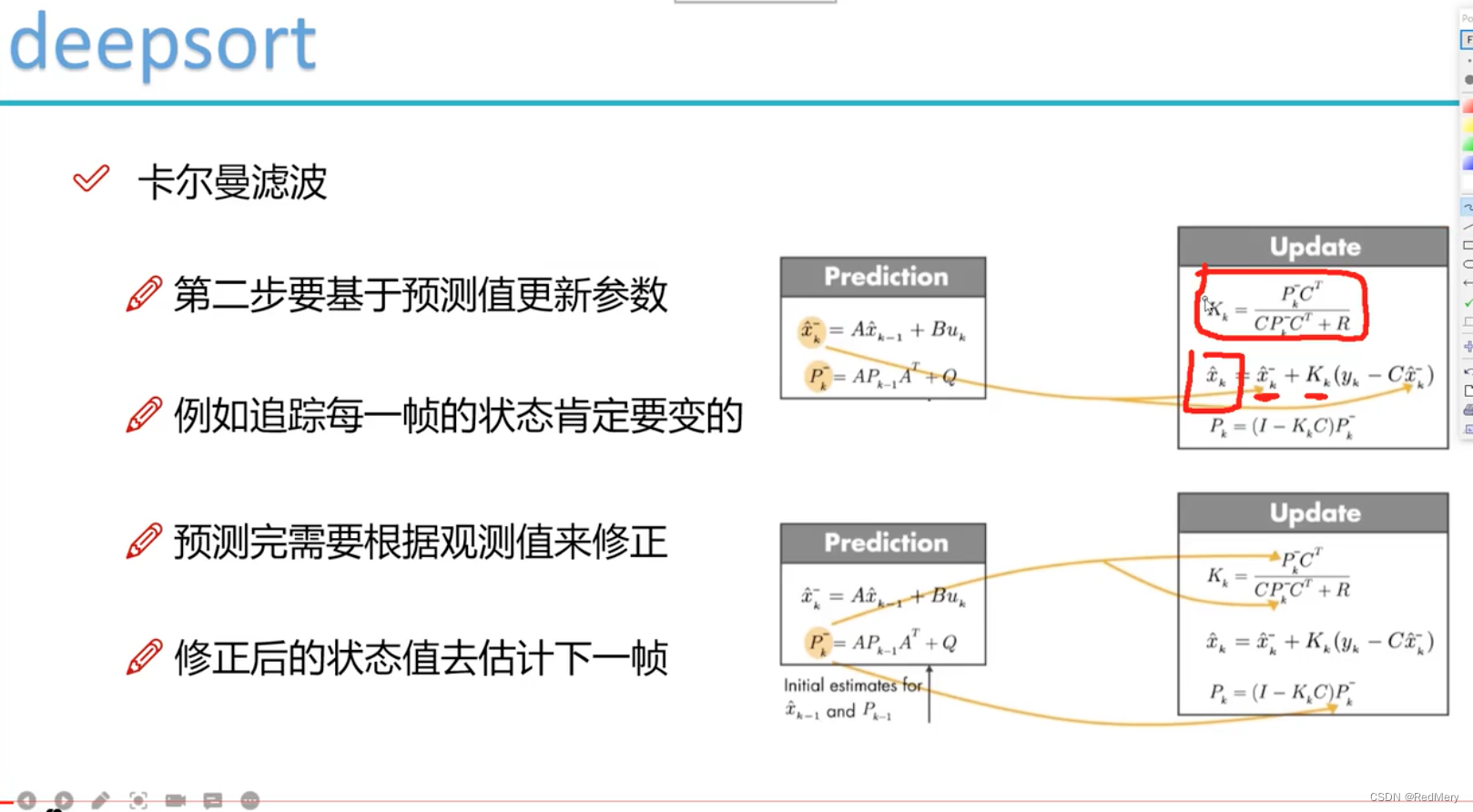
预测阶段
x ^ k − = A x ^ k − 1 \hat{x}_k^-=A\hat{x}_{k-1} x^k−=Ax^k−1
P k − = A P k − 1 A T + Q , P k − ∈ R 8 , 8 P_k^-=AP_{k-1}A^T+Q, P_k^- \in R^{8,8} Pk−=APk−1AT+Q,Pk−∈R8,8
更新阶段
K k = P k − C T C P k − C T + R , K k ∈ R 8 , 4 K_k=\frac{P_k^-C^T}{CP_k^-C^T+R}, K_k\in R^{8,4} Kk=CPk−CT+RPk−CT,Kk∈R8,4
x k ^ = x ^ k − + K k ( y k − C x ^ k − ) , C ∈ R 4 , 8 , x ^ k − ∈ R 8 , 1 , y k ∈ R 4 , 1 \hat{x_k}=\hat{x}_k^-+K_k(y_k-C\hat{x}_k^-), C\in R^{4,8}, \hat{x}_k^-\in R^{8,1}, y_k\in R^{4,1} xk^=x^k−+Kk(yk−Cx^k−),C∈R4,8,x^k−∈R8,1,yk∈R4,1
P k = ( I − K k C ) P k − P_k=(I-K_kC)P_k^- Pk=(I−KkC)Pk−
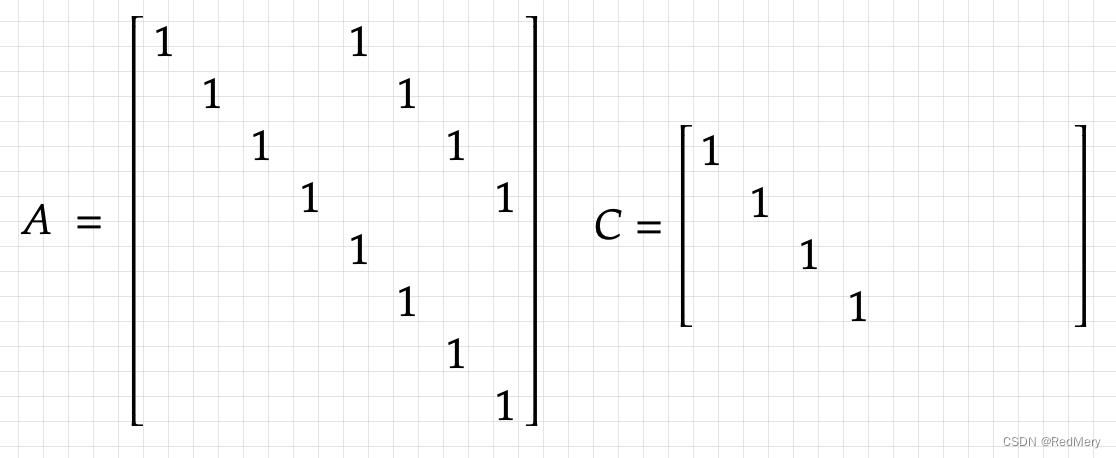
整个过程中,矩阵A和矩阵C保持不变,具体如下所示。C是状态观测矩阵,比如,如果我们现在的观测值是速度,而需要的是位置,那么C就是由速度变化到位置的变换矩阵。而在这里,C是由检测框变换到检测框的变换矩阵,因此C里都是1
 详细步骤:
详细步骤:
1.获得第一帧输出的检测框参数初始化
x ^ k − \hat{x}_k^- x^k−和 P k − P_k^- Pk−首先被初始化
x ^ 0 − = [ x , y , r , h , 0 , 0 , 0 , 0 ] , ∈ R 1 , 8 \hat{x}_0^-=[x,y,r,h,0,0,0,0], \in R^{1,8} x^0−=[x,y,r,h,0,0,0,0],∈R1,8
P k − P_k^- Pk−与 x ^ 0 − , ∈ R 8 , 8 \hat{x}_0^-, \in R^{8,8} x^0−,∈R8,8 有关,差了一个系数,代码如下所示
# self._std_weight_position = 0.05
# self._std_weight_velocity = 0.00625
std = [2 * self._std_weight_position * measurement[3], #2 * self._std_weight_position * measurement[3], 1e-2, 2 * self._std_weight_position * measurement[3], 10 * self._std_weight_velocity * measurement[3], 10 * self._std_weight_velocity * measurement[3], 1e-5, 10 * self._std_weight_velocity * measurement[3]]
covariance = np.diag(np.square(std))
2.预测下一时刻(第二帧中检测框的位置,图中的Prediction过程)
x ^ k − \hat{x}_k^- x^k−正常计算,
P k − 中的 Q P_k^-中的 Q Pk−中的Q是一个随机噪声,其为
std_pos = [ self._std_weight_position * mean[3], self._std_weight_position * mean[3], 1e-2, self._std_weight_position * mean[3]] std_vel = [self._std_weight_velocity * mean[3], self._std_weight_velocity * mean[3], 1e-5, self._std_weight_velocity * mean[3]] motion_cov = np.diag(np.square(np.r_[std_pos, std_vel])) mean = np.dot(self._motion_mat, mean)covariance = np.linalg.multi_dot(( self._motion_mat, covariance, self._motion_mat.T)) + motion_cov
3.完成配对,给每一个轨迹匹配一个检测框
4.更新过程(Update)
def project(self, mean, covariance): """Project state distribution to measurement space. Parameters ---------- mean : ndarray The state's mean vector (8 dimensional array). covariance : ndarray The state's covariance matrix (8x8 dimensional). Returns ------- (ndarray, ndarray) Returns the projected mean and covariance matrix of the given state estimate. """ std = [ self._std_weight_position * mean[3], self._std_weight_position * mean[3], 1e-1, self._std_weight_position * mean[3]] innovation_cov = np.diag(np.square(std)) mean = np.dot(self._update_mat, mean) covariance = np.linalg.multi_dot(( self._update_mat, covariance, self._update_mat.T)) return mean, covariance + innovation_covdef update(self, mean, covariance, measurement): """Run Kalman filter correction step. Parameters ---------- mean : ndarray The predicted state's mean vector (8 dimensional). covariance : ndarray The state's covariance matrix (8x8 dimensional). measurement : ndarray The 4 dimensional measurement vector (x, y, a, h), where (x, y) is the center position, a the aspect ratio, and h the height of the bounding box. Returns ------- (ndarray, ndarray) Returns the measurement-corrected state distribution. """ projected_mean, projected_cov = self.project(mean, covariance) #求解AX=b中的xchol_factor, lower = scipy.linalg.cho_factor(projected_cov, lower=True, check_finite=False) kalman_gain = scipy.linalg.cho_solve((chol_factor,lower), np.dot(covariance, self._update_mat.T).T, check_finite=False).T innovation = measurement - projected_mean new_mean = mean + np.dot(innovation, kalman_gain.T) new_covariance = covariance - np.linalg.multi_dot(( kalman_gain, projected_cov, kalman_gain.T)) return new_mean, new_covariance
本文在卡尔曼滤波:从入门到精通的基础上,又添加了一些个人的理解
导论
卡尔曼滤波本质上是一个数据融合算法,将具有同样测量目的、来自不同传感器、(可能) 具有不同单位 (unit) 的数据融合在一起,得到一个更精确的目的测量值。事实上,卡尔曼滤波是将两个高斯分布相乘而得到的一个新的高斯分布。
简述
首先考虑一个SLAM问题
- 运动方程: x t = F t ⋅ x t − 1 + B t ⋅ u t + ω t (1) x_t=F_t \cdot x_{t-1}+B_t\cdot u_t+\omega_t \tag{1} xt=Ft⋅xt−1+Bt⋅ut+ωt(1)
- 观测方程: z t = H t ⋅ x t + v t (2) z_t=H_t \cdot x_t+v_t \tag{2} zt=Ht⋅xt+vt(2)
其中:
x t x_t xt为 t t t 时刻的状态向量,包括了相机位姿、路标坐标等信息,也可能有速度、朝向等信息;
u t u_t ut为运动测量值,如加速度,转向等等;
F t F_t Ft为状态转换方程,将 t − 1 t-1 t−1 时刻的状态转换至 t t t 时刻的状态;
B t B_t Bt 是控制输入矩阵,将运动测量值 的作用映射到状态向量上;
ω t \omega_t ωt是预测的高斯噪声,其均值为0,协方差矩阵为 Q t Q_t Qt 。
z t z_t zt为传感器的测量值;
H t H_t Ht为转换矩阵,它将状态向量映射到测量值所在的空间中,由于估计值和预测值可能不同,单位也不同,因此需要 H t H_t Ht来进行变换。
v t v_t vt为测量的高斯噪声,其均值为0,协方差矩阵为 R t R_t Rt。
一个小例子:
用一个在解释卡尔曼滤波时最常用的一维例子:小车追踪。如下图所示:
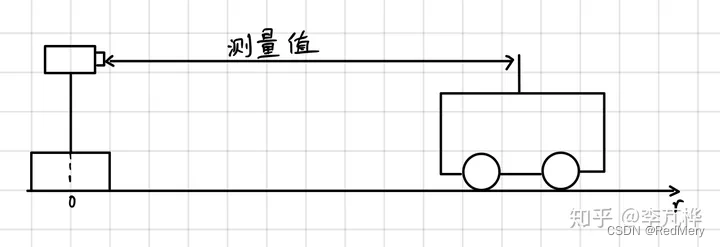
状态向量 x t x_t xt为小车的位置和速度:
x t = [ s t v t ] (3) x_t= \begin{bmatrix} s_t\\ v_t\\ \end{bmatrix} \tag{3} xt=[stvt](3)
其中, s t s_t st为t时刻的位移, v t v_t vt为t时刻的速度
{ s t = s t − 1 + v t ⋅ △ t + 1 2 ⋅ u t ⋅ △ t 2 v t = v t − 1 + u t ⋅ △ t (4) \begin{cases} s_t& =s_{t-1}+v_t\cdot \vartriangle t+\frac{1}{2}\cdot u_t\cdot \vartriangle t ^2\\ v_t& = v_{t-1} + u_t\cdot \vartriangle t \tag{4} \end{cases} {stvt=st−1+vt⋅△t+21⋅ut⋅△t2=vt−1+ut⋅△t(4)
写成矩阵的形式
[ s t v t ] = [ 1 △ t 0 1 ] [ s t − 1 v t − 1 ] + [ △ t 2 2 △ t ] ⋅ u t (5) \begin{bmatrix} s_t\\ v_t\\ \end{bmatrix}= \begin{bmatrix} 1&\vartriangle t\\ 0&1\\ \end{bmatrix} \begin{bmatrix} s_{t-1}\\ v_{t-1}\\ \end{bmatrix}+ \begin{bmatrix} \frac{\vartriangle t ^2}{2}\\ \vartriangle t\\ \end{bmatrix}\cdot u_t \tag{5} [stvt]=[10△t1][st−1vt−1]+[2△t2△t]⋅ut(5)
跟之前的运动方程对比,就知道
F t = [ 1 △ t 0 1 ] , B t = [ △ t 2 2 △ t ] F_t = \begin{bmatrix} 1&\vartriangle t\\ 0&1\\ \end{bmatrix},B_t= \begin{bmatrix} \frac{\vartriangle t ^2}{2}\\ \vartriangle t\\ \end{bmatrix} Ft=[10△t1],Bt=[2△t2△t]
上式就写为
x ^ t ∣ t − 1 = F t ⋅ x ^ t − 1 + B t ⋅ u t (6) \hat{x}_{t|t-1}=F_t\cdot\hat{x}_{t-1}+B_t\cdot u_t \tag{6} x^t∣t−1=Ft⋅x^t−1+Bt⋅ut(6)
与公式(1)的不同是,公式(1)中的值 x t x_t xt都是真实值,因此其中包含有误差,而公式(6)中的 x ^ t ∣ t − 1 \hat{x}_{t|t-1} x^t∣t−1是由运动学方程计算出来的,因此其中不包含误差。
联立公式(1)和(6)可得:
x t − x ^ t ∣ t − 1 = F ⋅ ( x t − 1 − x ^ t ∣ t − 1 ) + ω t x_t-\hat{x}_{t|t-1}=F\cdot (x_{t-1}-\hat{x}_{t|t-1})+\omega_t xt−x^t∣t−1=F⋅(xt−1−x^t∣t−1)+ωt
接下来计算真实值 x t x_t xt的协方差矩阵,首先明确一点矩阵 x t x_t xt是一个矩阵,它的形式如下所示:
x t = [ x 1 T , x 2 T , ⋯ , x n T ] = [ x 1 , 1 x 1 , 2 ⋯ x 1 , n − 1 x 1 , n x 2 , 1 x 2 , 2 ⋯ x 2 , n − 1 x 2 , n ⋮ ⋮ ⋮ ⋮ ⋮ x m , 1 x m , 2 ⋯ x 1 , m − 1 x 1 , m ] ∈ R m , n x_t=[x_1^T,x_2^T,\cdots,x_n^T]= \begin{bmatrix} x_{1,1}&x_{1,2}&\cdots&x_{1,n-1}&x_{1,n}\\ x_{2,1}&x_{2,2}&\cdots&x_{2,n-1}&x_{2,n}\\ \vdots&\vdots&\vdots&\vdots&\vdots\\ x_{m,1}&x_{m,2}&\cdots&x_{1,m-1}&x_{1,m}\\ \end{bmatrix}\in R^{m,n} xt=[x1T,x2T,⋯,xnT]= x1,1x2,1⋮xm,1x1,2x2,2⋮xm,2⋯⋯⋮⋯x1,n−1x2,n−1⋮x1,m−1x1,nx2,n⋮x1,m ∈Rm,n
也就是说 x t x_t xt中包含了n个状态量,并且每个状态量是一个m维向量,也就是存住了t个时刻的量。
还需要注意一点的是,且
x ^ t ∣ t − 1 \hat{x}_{t|t-1} x^t∣t−1为t时刻的状态矩阵 x t x_t xt 中不同状态量的均值。且
x ^ t ∣ t − 1 = [ m e a n ( x 1 ) m e a n ( x 2 ) ⋮ m e a n ( x n ) ] \hat{x}_{t|t-1}= \begin{bmatrix} mean(x_1)\\ mean(x_2)\\ \vdots\\ mean(x_n)\\ \end{bmatrix} x^t∣t−1= mean(x1)mean(x2)⋮mean(xn)
这也好理解,因为 x t x_t xt中应当是真实值,但是真实值事实上永远不可能知道的。不过呢,真实值的均值可以通过计算 x ^ t ∣ t − 1 \hat{x}_{t|t-1} x^t∣t−1得到,并且在均值的附近有误差,也就是一个在均值附近是一个高斯分布。那么接下来求矩阵 x t x_t xt的协方差矩阵就好理解了。
P t ∣ t − 1 = E [ ( x t − x ^ t ∣ t − 1 ) ( x t − x ^ t ∣ t − 1 ) T ] = E [ ( F ( x t − x ^ t ∣ t − 1 ) + ω t ) ⋅ ( F ( x t − x ^ t ∣ t − 1 ) + ω t ) T ] = F E [ ( x t − x ^ t ∣ t − 1 ) ⋅ ( x t − x ^ t ∣ t − 1 ) T ] F T + E [ F ( x t − x ^ t ∣ t − 1 ) ⋅ ω t T ] + E [ ω t ⋅ ( F ( x t − x ^ t ∣ t − 1 ) ) T ] + E [ ω t ⋅ ω t T ] \begin{equation} \begin{aligned} P_{t|t-1}&=E[(x_t-\hat{x}_{t|t-1})(x_t-\hat{x}_{t|t-1})^T] \\ & = E[(F(x_t-\hat{x}_{t|t-1})+\omega_t)\cdot (F(x_t-\hat{x}_{t|t-1})+\omega_t)^T] \\ & =FE[(x_t-\hat{x}_{t|t-1})\cdot (x_t-\hat{x}_{t|t-1})^T]F^T\\ &+E[F(x_t-\hat{x}_{t|t-1})\cdot \omega_t^T]+E[\omega_t\cdot (F(x_t-\hat{x}_{t|t-1}))^T] \\ &+E[\omega_t \cdot \omega_t^T] \end{aligned} \tag{} \end{equation} Pt∣t−1=E[(xt−x^t∣t−1)(xt−x^t∣t−1)T]=E[(F(xt−x^t∣t−1)+ωt)⋅(F(xt−x^t∣t−1)+ωt)T]=FE[(xt−x^t∣t−1)⋅(xt−x^t∣t−1)T]FT+E[F(xt−x^t∣t−1)⋅ωtT]+E[ωt⋅(F(xt−x^t∣t−1))T]+E[ωt⋅ωtT]()
其中 E [ F ( x t − x ^ t ∣ t − 1 ) ⋅ ω t T ] E[F(x_t-\hat{x}_{t|t-1})\cdot \omega_t^T] E[F(xt−x^t∣t−1)⋅ωtT]表示矩阵 F ( x t − x ^ t ∣ t − 1 ) F(x_t-\hat{x}_{t|t-1}) F(xt−x^t∣t−1) 与 ω t T \omega_t^T ωtT矩阵的协方差,且由于这两者这件并无关系,所以
E [ F ( x t − x ^ t ∣ t − 1 ) ⋅ ω t T ] = 0 E[F(x_t-\hat{x}_{t|t-1})\cdot \omega_t^T] =0 E[F(xt−x^t∣t−1)⋅ωtT]=0同理
E [ ω t ⋅ ( F ( x t − x ^ t ∣ t − 1 ) ) T ] = 0 E[\omega_t\cdot (F(x_t-\hat{x}_{t|t-1}))^T]=0 E[ωt⋅(F(xt−x^t∣t−1))T]=0
注意公式中的E表示的是期望,这里是由于协方差的计算方式不同,在matlab中的计算公式课本上的有所不同,这里知道就可以了。
因此就可以得到协方差的预测公式
P t ∣ t − 1 = F E [ ( x t − x ^ t ∣ t − 1 ) ⋅ ( x t − x ^ t ∣ t − 1 ) T ] F + E [ ω t ⋅ ω t T ] = F P t − 1 F T + Q t \begin{equation} \begin{aligned} P_{t|t-1}& =FE[(x_t-\hat{x}_{t|t-1})\cdot (x_t-\hat{x}_{t|t-1})^T]F+E[\omega_t \cdot \omega_t^T]\\ &=FP_{t-1}F^T+Q_t \end{aligned} \tag{} \end{equation} Pt∣t−1=FE[(xt−x^t∣t−1)⋅(xt−x^t∣t−1)T]F+E[ωt⋅ωtT]=FPt−1FT+Qt()
由以上的步骤,我们就得到了预测值和预测值的协方差矩阵,接下来就需要将预测值与观测值进行融合了。由于预测值是符合高斯分布,观测值也符合高斯分布,那么融合的本质就是将这个两个高斯分布乘起来,乘起来还是一个高斯分布,那么乘起来之后的高斯分布的均值和方差的公式推导,见帖子两个高斯分布乘积的理论推导
现在我们有n个预测量,假设有k个观测量为
x t − x ^ t ∣ t − 1 = F ⋅ ( x t − 1 − x ^ t ∣ t − 1 ) + ω t x_t-\hat{x}_{t|t-1}=F\cdot (x_{t-1}-\hat{x}_{t|t-1})+\omega_t xt−x^t∣t−1=F⋅(xt−1−x^t∣t−1)+ωt
接下来计算真实值 x t x_t xt的协方差矩阵,首先明确一点矩阵 x t x_t xt是一个矩阵,它的形式如下所示:
z t = [ z 1 z 2 ⋮ z n ] z_t= \begin{bmatrix} z_1\\ z_2\\ \vdots\\ z_n\\ \end{bmatrix} zt= z1z2⋮zn
x t x_t xt与 z t z_t zt 之间由于单位不同,因此需要使用一个转化矩阵H,即
z t = H ⋅ x t z_t=H\cdot x_t zt=H⋅xt写成矩阵形式就是
[ z 1 z 2 ⋮ z k ] = H ⋅ [ x 1 x 2 ⋮ x n ] \begin{bmatrix} z_1\\ z_2\\ \vdots\\ z_k\\ \end{bmatrix}= H\cdot \begin{bmatrix} x_{1}\\ x_{2}\\ \vdots\\ x_{n}\\ \end{bmatrix} z1z2⋮zk =H⋅ x1x2⋮xn
相关文章:

DeepSORT中的卡尔曼滤波
本文是看了DeepSORT方法视频之后,关于其中使用的卡尔曼滤波的理解 DeepSORT视频链接 首先贴几个比较好的,与本文由有关的几个帖子 图说卡尔曼滤波,一份通俗易懂的教程 卡尔曼滤波(Kalman Filter)原理与公式推导 卡尔…...
【Linux网络服务】SSH远程访问及控制
一、openssh服务器 1.1ssh协议 SSH(Secure Shell)是一种安全通道协议,主要用来实现字符界面的远程登录、远程 复制等功能; SSH 协议对通信双方的数据传输进行了加密处理,其中包括用户登录时输入的用户口令࿱…...
AutoGPT的出现,会让程序员失业吗?
最近,一个叫AutoGPT的模型火了,在GitHub上线数周Star数就直线飙升。截至目前,AutoGPT的Star数已经达到87k,马上接近90k,超过了PyTorch的65k。 根据AutoGPT的命名,就可以发现其神奇之处在于“auto”&#x…...
微信小程序php+vue 校园租房指南房屋租赁系统
本着诚信的原则,平台必须要掌握出租方必要的真实可信的信息,这样就可以防止欺诈事件的发生,事后也可以联系找到出租方。并且租金等各方面规范标准化,在这易租房诚信可信的平台让承租方与出租方充分有效对接,既方便了承…...
水果FL Studio21最新中文完整版下载更新及内容介绍
简单总结一下,本次小版本更新最重要的内容,我个人认为是对于M1芯片的适配。其余的比如EQ2,3x这些我们很熟悉的插件虽说也有更新,但是估计并没有特别大的改动。我个人的话会先放一段时间,等下次有其他更让我感兴趣的内容…...

springboot+vue小区物业管理系统(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的小区物业管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者:风…...
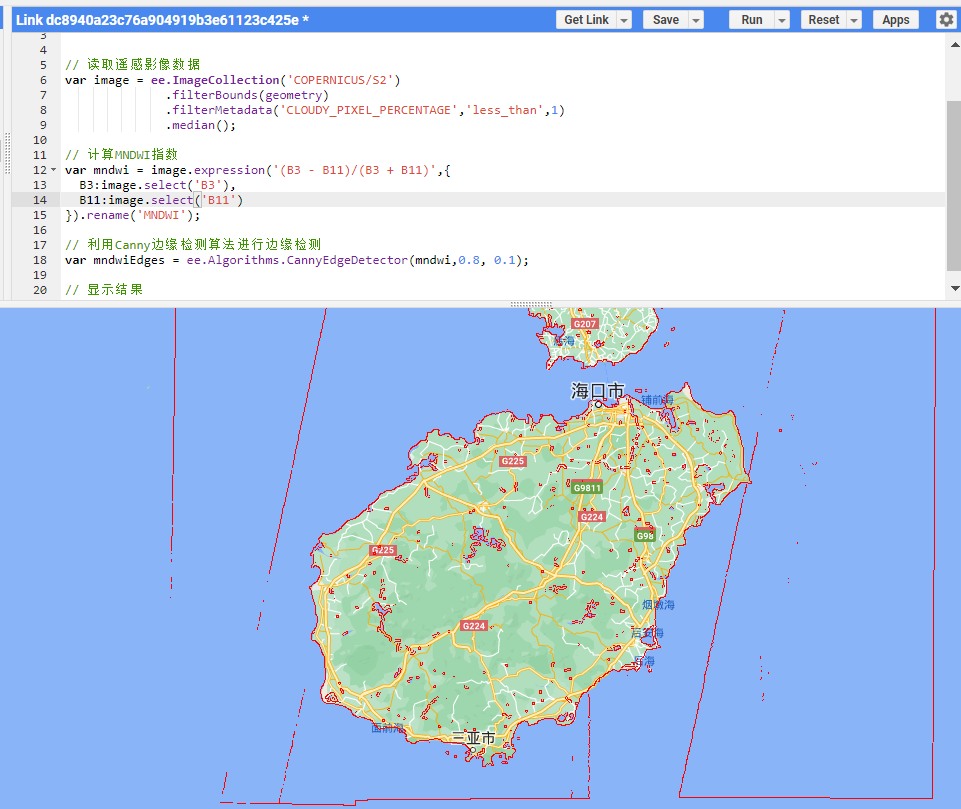
GEEer成长日记二十三:chatGPT可以帮我们提取水体边缘吗?
欢迎关注公众号:GEEer成长日记 目录 01 首先,chatGPT是什么? 02 进入正题,如何进行边缘检测? chatGPT推出之后,引发了激烈的讨论,今天带各位看看它在GEE方面能为我们做什么。原本想着它可以…...
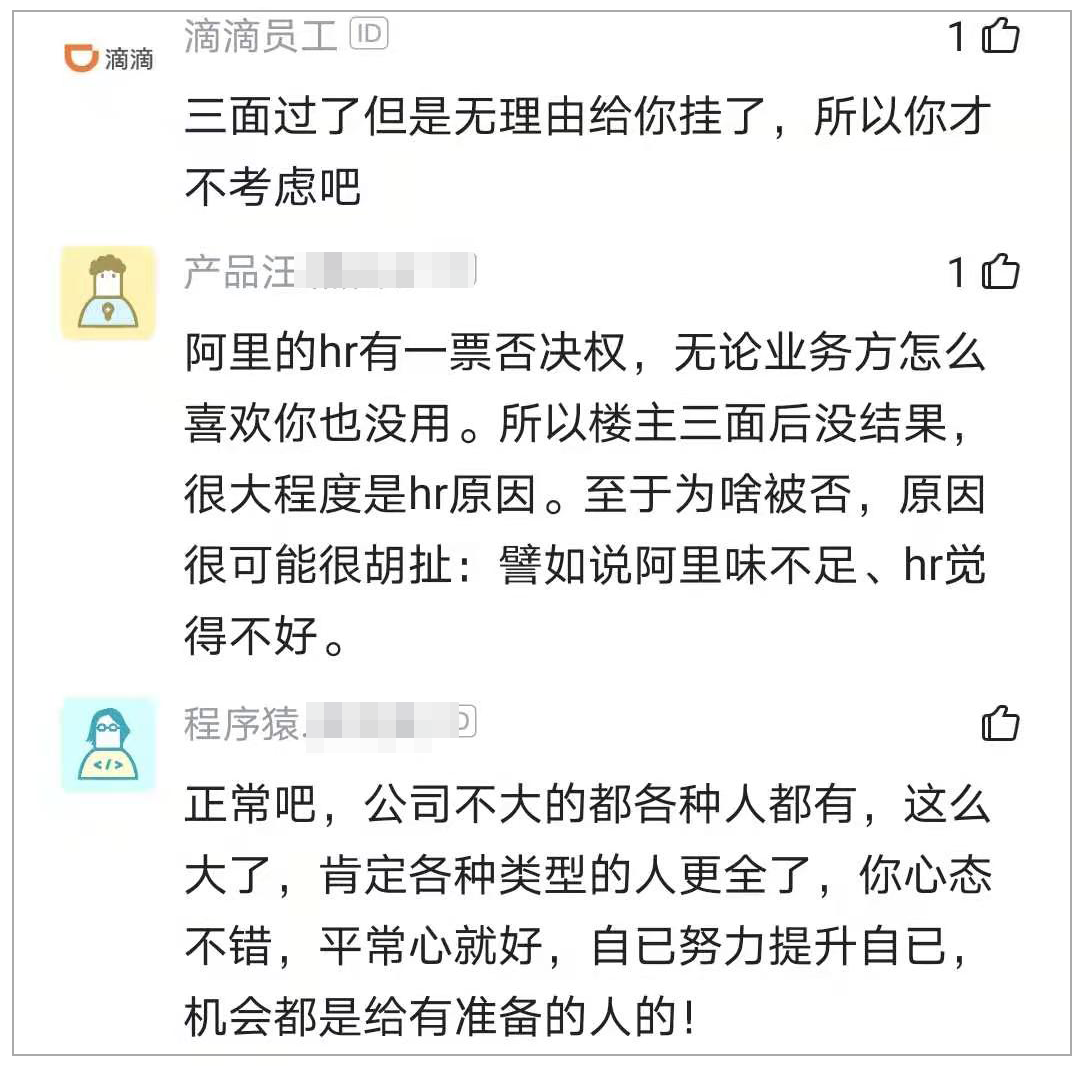
程序员阿里三面无理由挂了,被HR一句话噎死,网友:这可是阿里啊
进入互联网大厂一般都是“过五关斩六将”,难度堪比西天取经,但当你真正面对这些大厂的面试时,有时候又会被其中的神操作弄的很是蒙圈。 近日,某位程序员发帖称,自己去阿里面试,三面都过了,却被…...
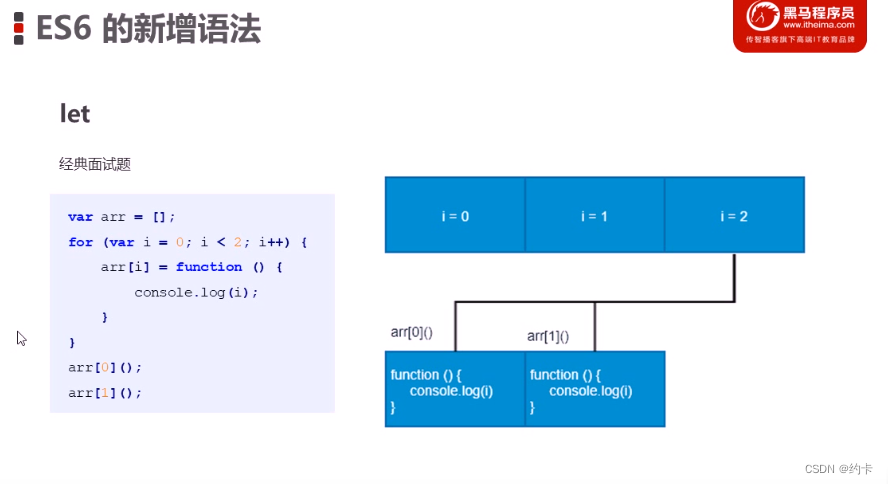
js面试题
在全局作用域下声明了一个变量 arr, 它的初始值是一个空数组 第二段代码,循环计数器变量i的初始值为0,循环条件是i的值小于2, 也就是说当i的值为0或者1时, 循环条件才能成立 才能够进入到循环体 当i的值为2时循环条件不成立&…...

SpringCloud --- Gateway服务网关
一、简介 Spring Cloud Gateway 是 Spring Cloud 的一个全新项目,该项目是基于 Spring 5.0,Spring Boot 2.0 和 Project Reactor 等响应式编程和事件流技术开发的网关,它旨在为微服务架构提供一种简单有效的统一的 API 路由管理方式。 二、为…...
【java】CGLIB动态代理原理
文章目录 1. 简介2. 示例3. 原理4. JDK动态代理与CGLIB动态代理区别(面试常问) 1. 简介 CGLIB的全称是:Code Generation Library。 CGLIB是一个强大的、高性能、高质量的代码生成类库,它可以在运行期扩展Java类与实现Java接口&a…...
ArcGIS Pro、Python、USLE、INVEST模型等多技术融合的生态系统服务构建生态安全格局
第一章、生态安全评价理论及方法介绍 一、生态安全评价简介 二、生态服务能力简介 三、生态安全格局构建研究方法简介 第二章、平台基础一、ArcGIS Pro介绍1. ArcGIS Pro简介2. ArcGIS Pro基础3. ArcGIS Pro数据编辑4. ArcGIS Pro空间分析5. 模型构建器6. ArcGIS Pro…...

openstack安装应答文件时报错处理
环境:centos7 在执行packstack --answer-file./answer.ini命令后,一般需要几分钟才能完成,如何在applying IP controler.pp时报错,需要注意以下几点: 0.关闭firewalld和selinux(必须) system…...
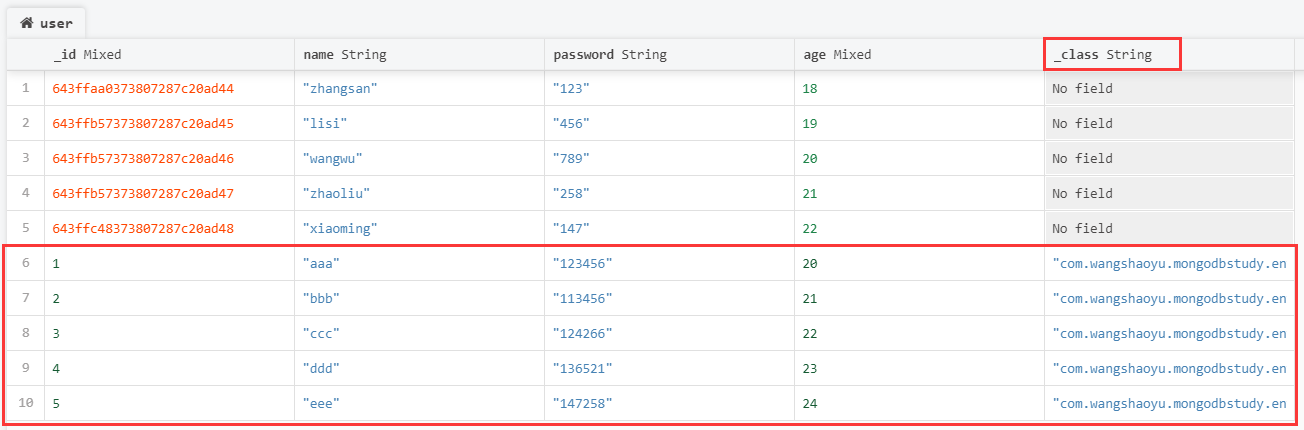
SpringBoot整合MongoDB
文章目录 一、环境准备二、集合操作三、文档操作3.1 实体类3.2 添加文档3.3 查询文档3.4 修改文档3.5 删除文档 提示:以下是本篇文章正文内容,MongoDB 系列学习将会持续更新 一、环境准备 ①添加 SpringData 依赖: <dependency><…...

线程同步机制与互斥锁
线程同步机制 在多线程编程,一些敏感数据不允许被多个线程同时访问,此时就使用同步访问技术,保证数据在任何时刻,最多有一个线程访问,以保证数据的完整性。也可以这里理解:线程同步,即当有一个线程在对内存…...

Python算法设计 - 编码加密
一、编码加密 编码加密应用十分广泛,特别是在大数据时代,也因此信息安全变得尤为重要 有时我会读到“OTP是一种无法被破解的加密方式”,当然,文末会附上一个完全被破解的OTP加密的例子 问题在于,人们经常会觉得完美的…...
数据结构和算法学习记录——平衡二叉树(基本介绍、平衡因子、平衡二叉树的定义、平衡二叉树的高度)
目录 基本介绍 平衡因子 平衡二叉树 平衡二叉树的高度 基本介绍 什么是平衡二叉树? 以一个例子来解释一下: 搜索树结点按不同的插入次序,将会导致不同的深度和平均查找长度ASL 在二叉搜索树中查找一个元素: (…...
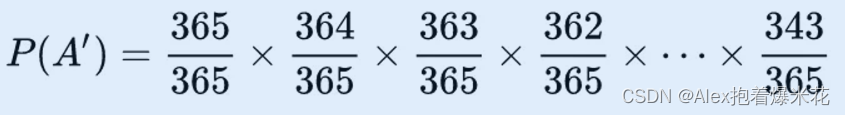
【浓缩概率】浓缩概率思想帮我蒙选择题的概率大大提升!
今天在学习的时候遇到一个很有趣的思想叫作浓缩概率,可以帮我们快速解决一下概率悖论问题! 什么是概率 计算概率有下面两个最简单的原则: 原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现…...
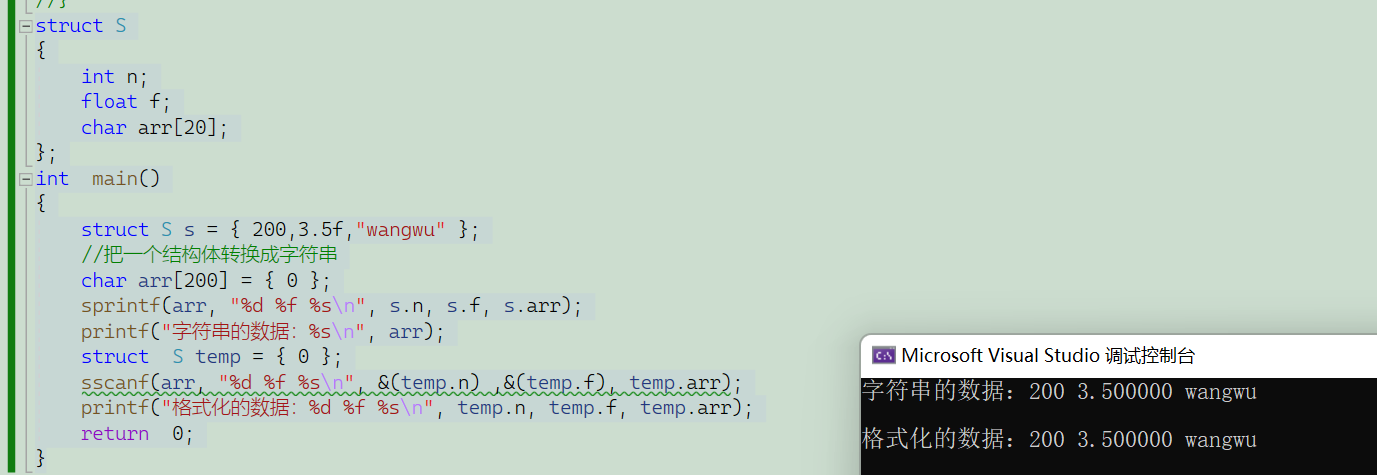
两小时让你全方位的认识文件(一)
想必友友们在生活中经常会使用到各种各样的文件,那么我们是否了解它其中的奥秘呢,今天阿博就带领友友们深入地走入文件🛩️🛩️🛩️ 文章目录 一.为什么使用文件二.什么是文件三.文件的打开和关闭四.文件的顺序读写 一…...

基于Java+Springboot+vue网上商品订单转手系统设计和实现
基于JavaSpringbootvue网上商品订单转手系统设计和实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
