数据结构和算法学习记录——平衡二叉树(基本介绍、平衡因子、平衡二叉树的定义、平衡二叉树的高度)
目录
基本介绍
平衡因子
平衡二叉树
平衡二叉树的高度
基本介绍
什么是平衡二叉树?
以一个例子来解释一下:
搜索树结点按不同的插入次序,将会导致不同的深度和平均查找长度ASL
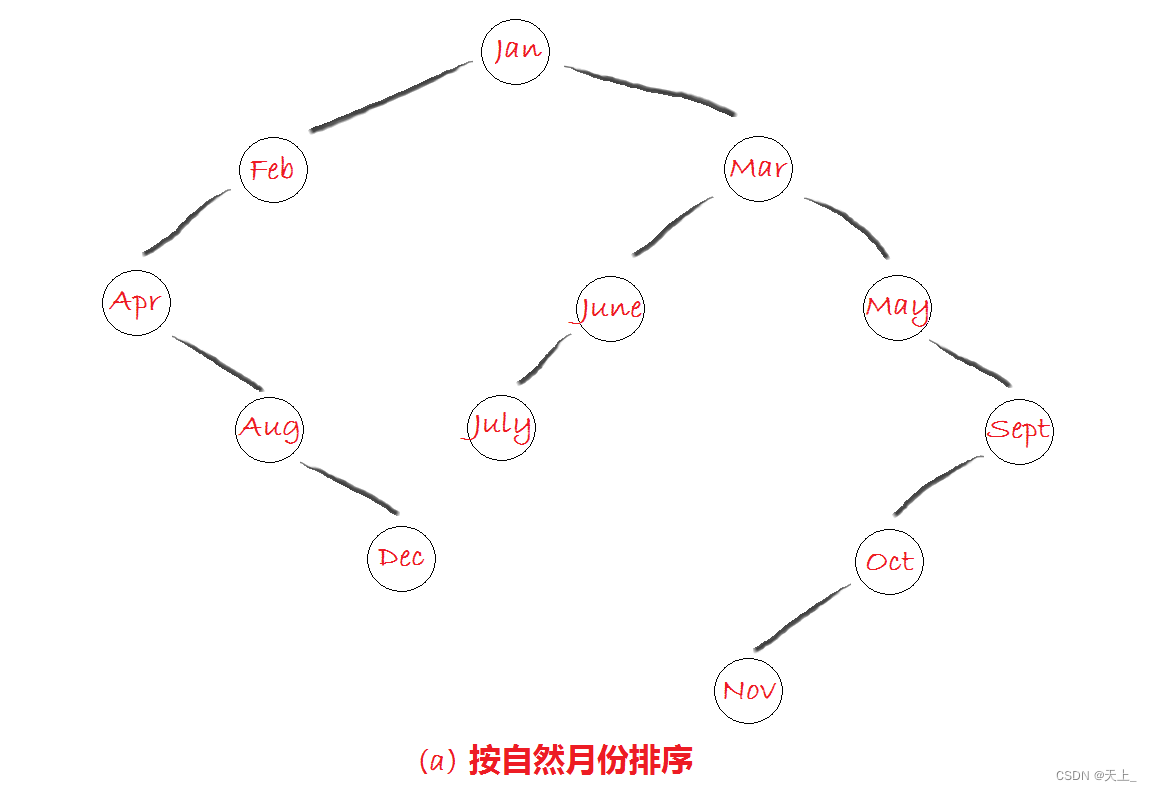
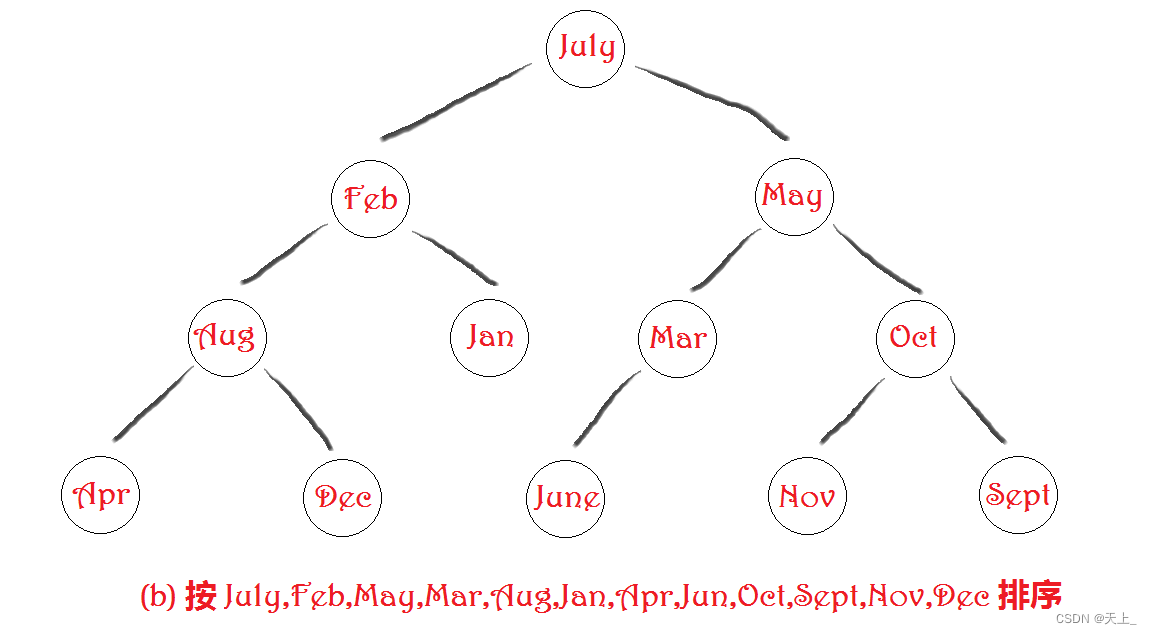

在二叉搜索树中查找一个元素:
(a)要找到Jan,需要查找一次;要找到Feb,需要查找两次;
要找到Mar,也需要查找两次......要找到Nov,需要查找六次。
把所有查找次数加起来,再除以12,
得到平均查找长度:ASL(a) = ( 1 + 2 * 2 + 3 * 3 + 4 * 3 + 5 * 2 + 6 * 1 ) / 12 = 3.5
(b)要找到July,需要查找一次;要找到Feb,需要查找两次;
要找到May,也需要查找两次......要找到Sept,需要查找四次。
算出平均查找长度:ASL(b) = (1 + 2 * 2 + 3 * 4 + 4 * 5) / 12 = 3.0
(c)要找到Apr,需要查找一次;要找到Aug,需要查找两次......
要找到Sept,需要查找十二次。
算出平均查找长度:ASL(c) = ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) / 12 = 6.5
通过上面的例子,我们可以看到方式b的平均查找长度最短,在观感上结点的分布也比较均匀。
所以二叉树,我们要求比较平衡,才能够让查找的长度更短一些。
而如何衡量一颗二叉树平衡不平衡呢?
- 是左右两边的结点数差不多
- 是左右两边的高度差不多
这样我们就认为基本上平衡,即为平衡二叉树。
平衡因子
平衡因子(Balance Factor,简称BF):
BF(T) =
-
, 其中
和
分别为T的左、右子树的高度。
平衡二叉树
平衡二叉树(Balanced Binary Tree) (AVL树)
空树,或者任一结点左、右子树高度差的绝对值不超过1,即
下面来判断一下以下几颗二叉树是否为平衡二叉树:
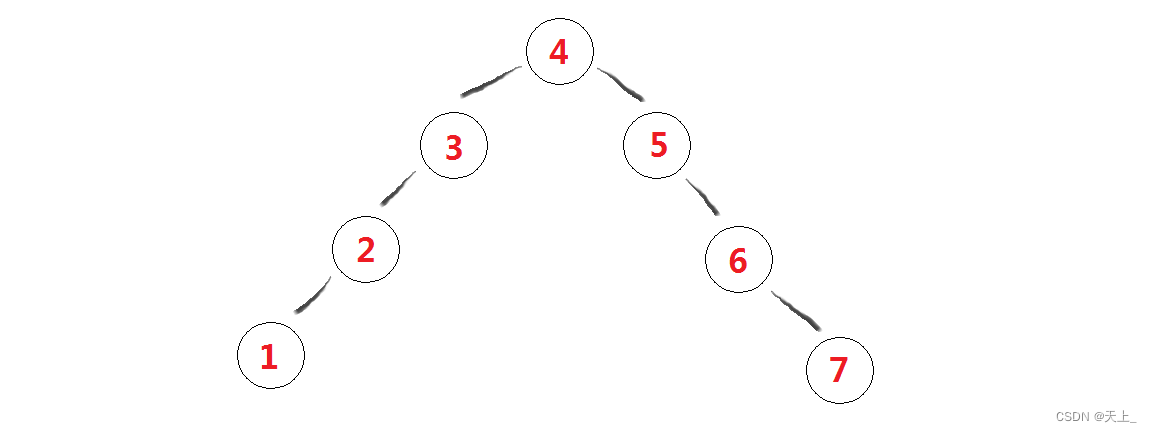
(1)
(2)
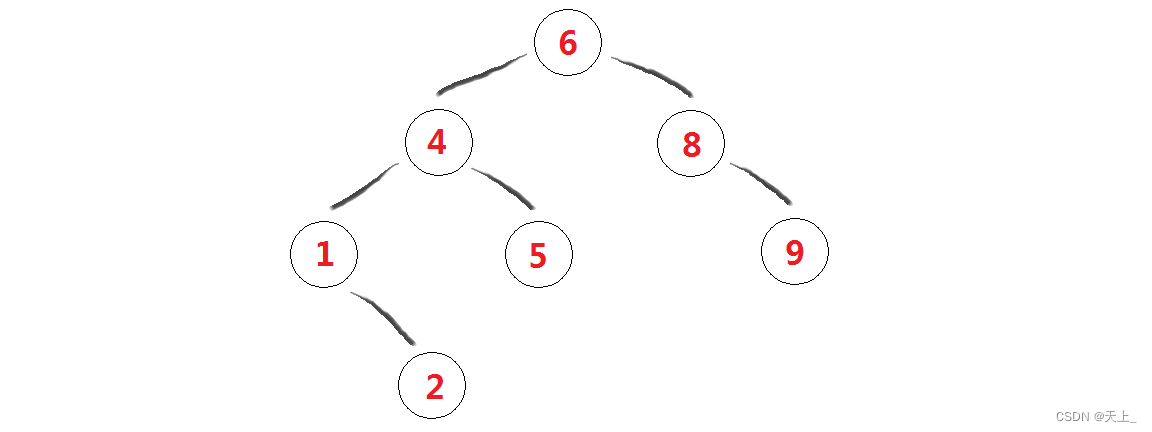
(3)
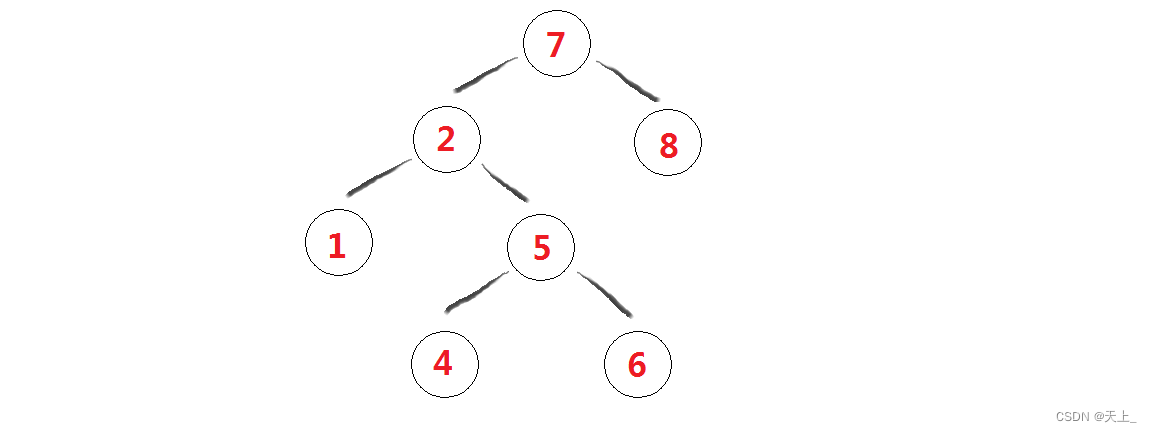
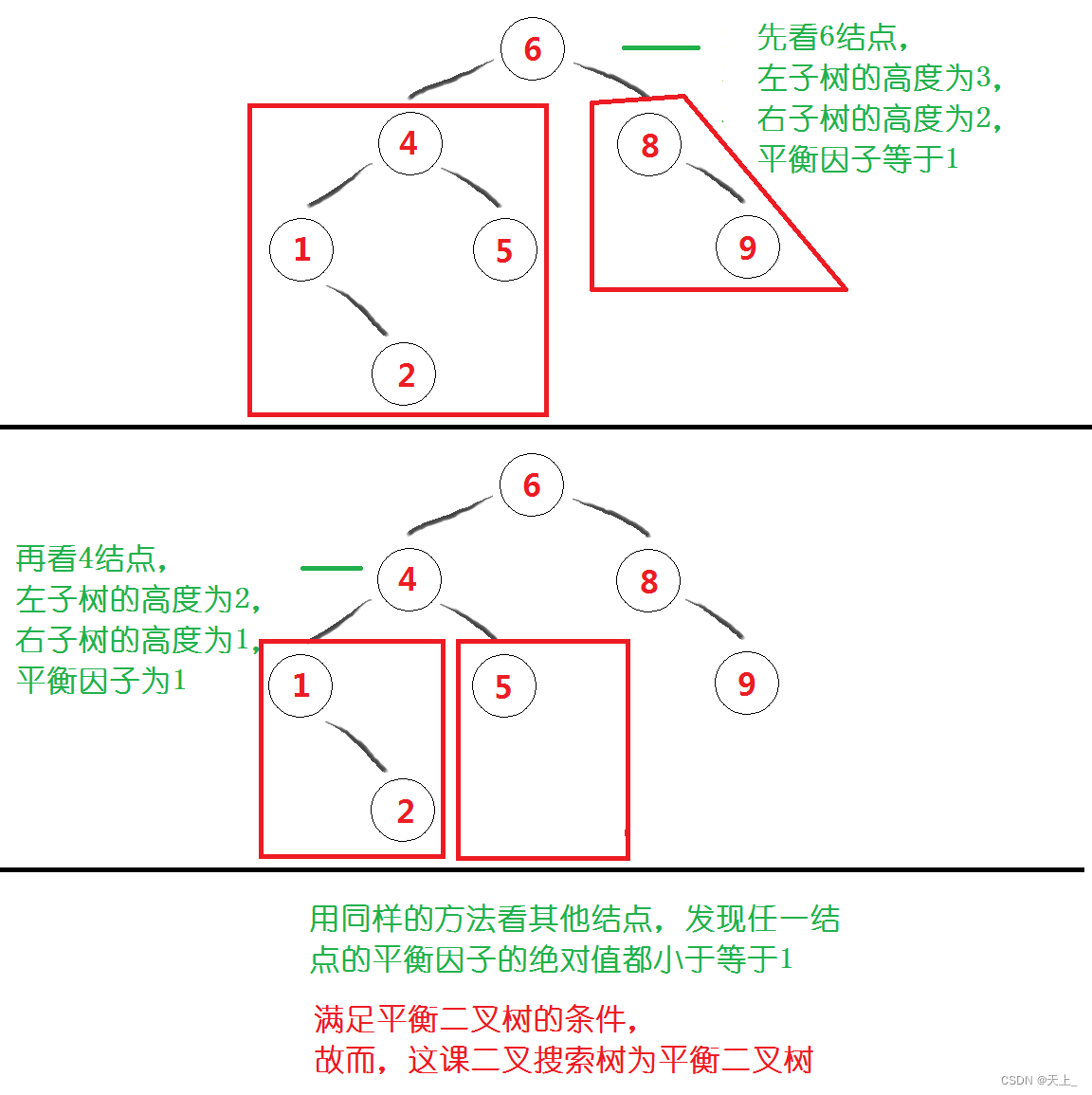
先来看第一棵二叉搜索树:

再来看第二棵二叉搜索树:
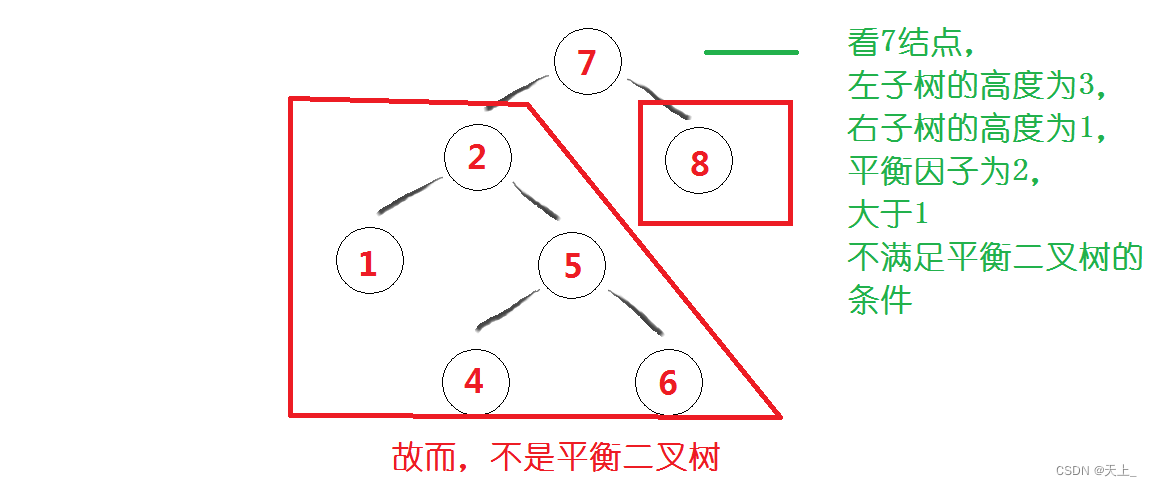
最后看第三棵二叉搜索树:
平衡二叉树的高度
我们要二叉树平衡,其目的是为了让二叉树的高度更低一些,
越平衡的二叉树高度就越低。
一棵结点总数为n的完全二叉树高度为 h = log2n,

那么平衡二叉树的高度是否能达到呢?
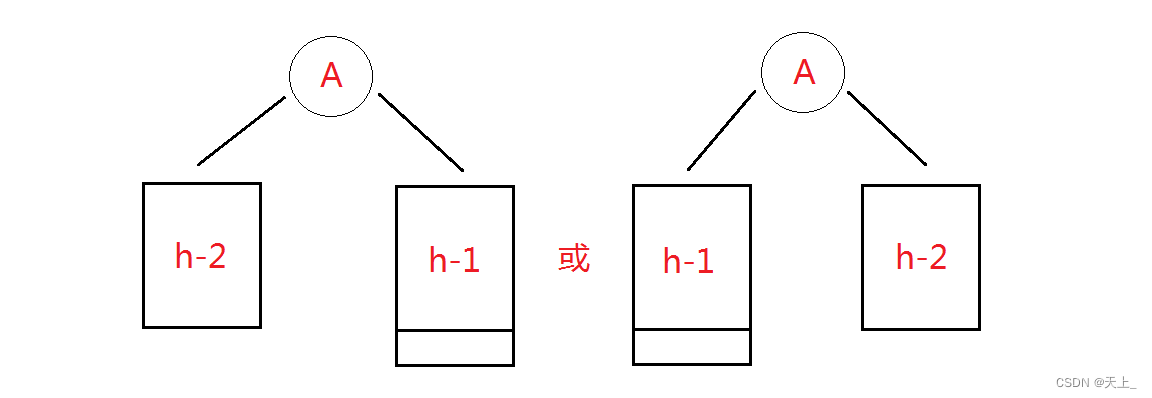
设为 高度为h的平衡二叉树的最少结点数。 结点数最少时:

总结出:
可以得到一个公式:
我们会发现,这个公式有点眼熟,是与斐波那契序列的公式有点像。
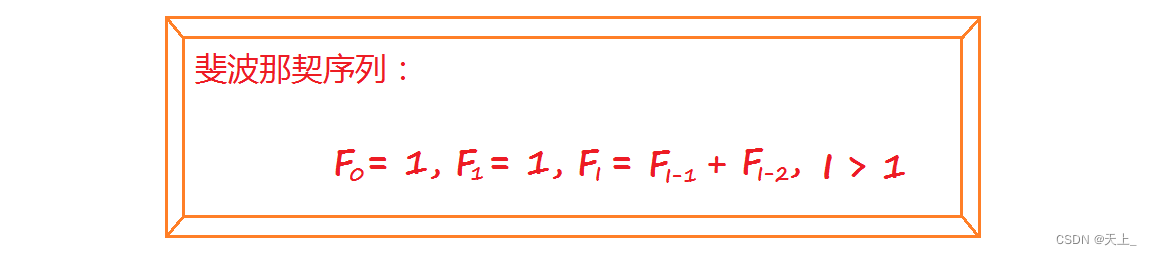
从这里我们就来分析一下nh跟斐波那契序列的有什么关系。
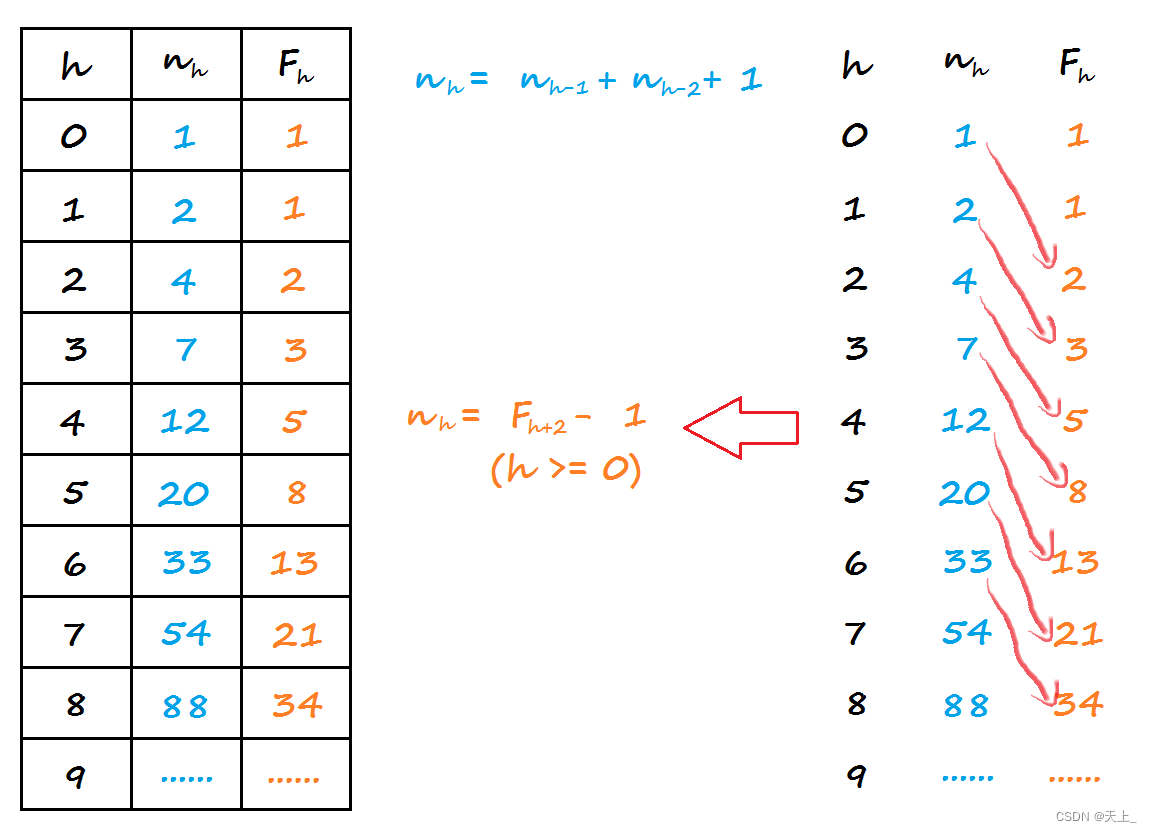
在数学上,有一个公式:
当i逐步增大时,大致等于公式算出来的值。
且是一个指数函数。
根据我们上面分析出来的和
的关系,就可以代入得到
的相关公式。
所以反过来我们就得到h的表达式:
用自己的想法把他推一遍:

综上所述,我们可以得到结论:
给定结点数为n的AVL树的最大高度为
end
学习自:MOOC数据结构——陈越、何钦铭
相关文章:
数据结构和算法学习记录——平衡二叉树(基本介绍、平衡因子、平衡二叉树的定义、平衡二叉树的高度)
目录 基本介绍 平衡因子 平衡二叉树 平衡二叉树的高度 基本介绍 什么是平衡二叉树? 以一个例子来解释一下: 搜索树结点按不同的插入次序,将会导致不同的深度和平均查找长度ASL 在二叉搜索树中查找一个元素: (…...
【浓缩概率】浓缩概率思想帮我蒙选择题的概率大大提升!
今天在学习的时候遇到一个很有趣的思想叫作浓缩概率,可以帮我们快速解决一下概率悖论问题! 什么是概率 计算概率有下面两个最简单的原则: 原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现…...
两小时让你全方位的认识文件(一)
想必友友们在生活中经常会使用到各种各样的文件,那么我们是否了解它其中的奥秘呢,今天阿博就带领友友们深入地走入文件🛩️🛩️🛩️ 文章目录 一.为什么使用文件二.什么是文件三.文件的打开和关闭四.文件的顺序读写 一…...

基于Java+Springboot+vue网上商品订单转手系统设计和实现
基于JavaSpringbootvue网上商品订单转手系统设计和实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式…...

旅游-商场购物
标题 前言必学场景词汇及用法售货员接待促销活动选购商品询问材质与质量试穿衣服杀价修改衣服结账售后服务退换货情境常用单词化妆品类别护肤品类别护肤品功能前言 加油 必学场景词汇及用法 售货员接待 1.be of service to sb 服务某人 Hello, ma’am. Could I be of serv…...

毕业论文用什么流程图软件比较好?
在写作论文的时候使用流程图,会让我们的论文看起来更加有逻辑。并且流程图的图片都可以在PPT中随意插入以及使用。 基础流程图作为最为基本和简单的的流程图方式,一般不区分用户角色和场景,适用于简单场景,梳理单一的流程情况&am…...
、322.零钱兑换、279.完全平方数)
算法刷题|70.爬楼梯(进阶)、322.零钱兑换、279.完全平方数
爬楼梯(进阶) 题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 思路:本题也可以抽象成完全背包的问题,背包就是总共多少阶台阶&am…...
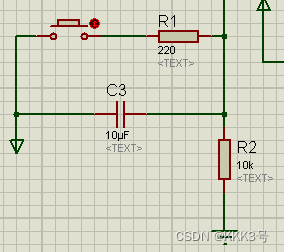
【MCS-51】51单片机结构原理
至今为止,MCS-51系列单片机有许多种型号的产品:其中又分为普通型51(8031、8051、89S51)和增强型52(8032、8052、89S52等)。它们最大的区别在于存储器配置各有差异。下面我举例子的都是8051这一系列的单片机…...
)
软件测试技术之如何编写测试用例(3)
14、对于类似于手机版淘宝这种软件,它拥有客户端,服务器端还有一个后台管理系统类似于进销存管理系统,我如何设计测试用例才能保证功能的完全覆盖?他们之间的交互如何设计测试用例? 专家分析:对于复合型的…...

移远通信笔试题
限时60分钟 1.下列关于栈叙述正确的是 A A) 栈顶元素最先能被删除 B)栈顶元素最后才能被删除 C)栈底元素永远不能被删除 D)以上三种都不对 在栈中,最后被压入的元素总是在栈顶上方,而栈顶元素总是最先被弹出的元…...
)
python算法中的机器学习算法之监督学习知识点(详解)
目录 学习目标: 学习内容: Ⅰ. 线性回归(Linear Regression) Ⅱ. 逻辑回归(Logistic Regression)...

Flink主要有两种基础类型的状态:keyed state
Flink主要有两种基础类型的状态:keyed state 和operator state。 Keyed State Keyed State总是和keys相关,并且只能用于KeyedStream上的函数和操作。 你可以将Keyed State视为是已经被分片或分区的Operator State,每个key都有且仅有一个状态分…...
js录音支持h5 pc ios android
最近在做h5录音的页面要求可暂停录音,继续录音,写好后发现不兼容ios,无奈只能找兼容方法,找了一天也没找到,后来看到一个网站在ios上可以暂停录音,后来引入他的js文件果然能用了 网站放下面了 Recorder H5: 用于html5网页中的前…...

mybatis04-mybatis缓存、分页插件、注解开发(一对一、多对一、多对多)
mybatis04 mybatis 缓存 一、mybatis 缓存概述 1、缓存 缓存 是存在于内存中的临时数据,使用缓存的目的是:减少和数据库的交互次数,提高执行效率。 2、mybatis 缓存 mybatis 与 大多数的持久层框架一样,提供了缓存策略…...

软件平台接口常见问题汇总
接口常见问题汇总 一、接口技术层面 1、输入参数验证校验不全面。如: 1.1入参数据类型长度边界,范围边界。 1.2 入参数据内容、成员内容,有效无效,合法非法。 1.3 入参数据 特殊字符 敏感字符过滤。 1.4 入参可否必选。 2、接口…...
SparkStreaming学习之——无状态与有状态转化、遍历kafka的topic消息、WindowOperations
目录 一、状态转化 二、kafka topic A→SparkStreaming→kafka topic B (一)rdd.foreach与rdd.foreachPartition (二)案例实操1 1.需求: 2.代码实现: 3.运行结果 (三)案例实操2 1.需求: 2.代码实现: 3.运行结果 三、W…...
)
上市公司碳排放测算数据(1992-2022年)
根据《温室气体核算体系》,企业的碳排放可以分为三个范围。 范围一是直接温室气体排放,产生于企业拥有或控制的排放源,例如企业拥有或控制的锅炉、熔炉、车辆等产生的燃烧排放;拥有或控制的工艺设备进行化工生产所产生的排放。 范…...
Springboot 整合 JPA 及 Swagger2
首先是官方文档: Spring Data JPA - Reference Documentationhttps://docs.spring.io/spring-data/jpa/docs/2.2.4.RELEASE/reference/html/#repositories.query-methods 1、JPA相关概念 2、创建 Springboot 项目 修改 pom 文件,可以直接进行复制粘贴&a…...
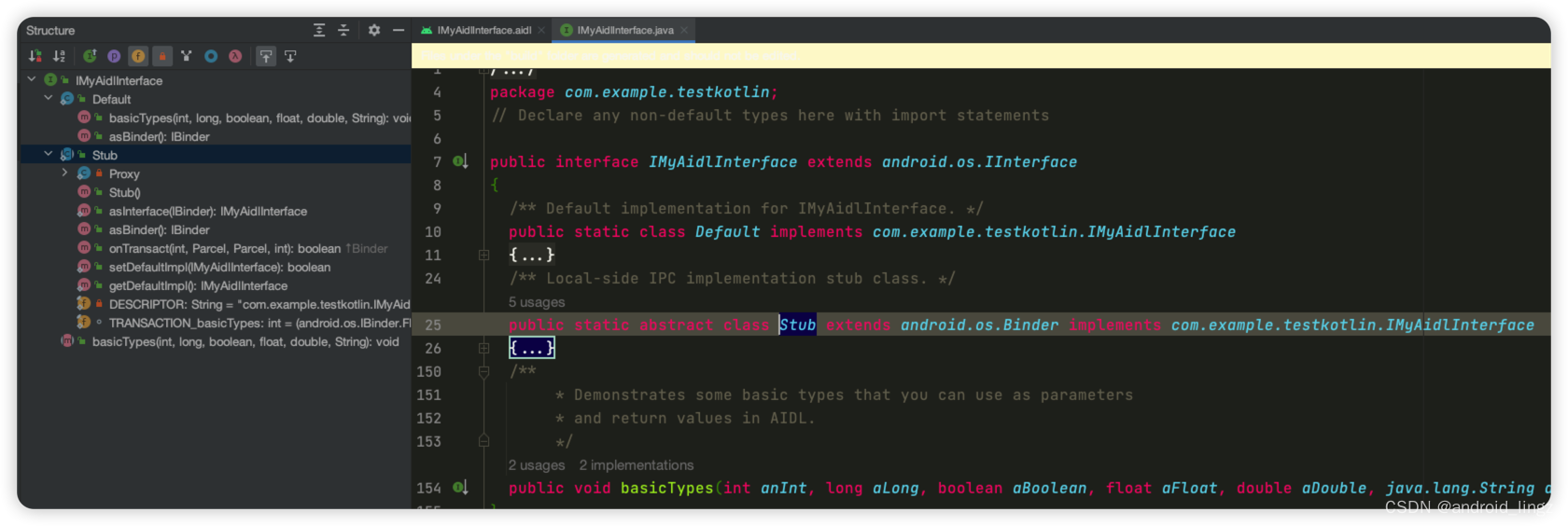
android aidl
本文只是记录个人学习aidl的实现,如需学习请参考下面两篇教程 官方文档介绍Android 接口定义语言 (AIDL) | Android 开发者 | Android Developers 本文参考文档Android进阶——AIDL详解_android aidl_Yawn__的博客-CSDN博客 AIDL定义:Android 接口…...
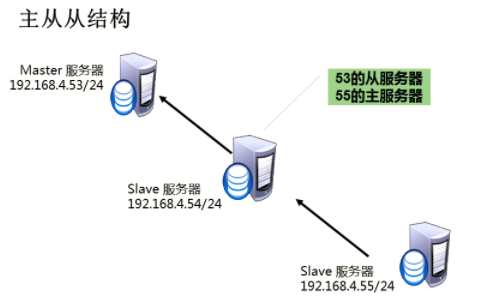
MYSQL---主从同步概述与配置
一、MYSQL主从同步概述 1、什么是MySQL主从同步? 实现数据自动同步的服务结构 主服务器(master): 接受客户端访问连接 从服务器(slave):自动同步主服务器数据 2、主从同步原理 Maste:启用binlog 日志 Slave:Slave_IO: 复制master主…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
