算法刷题|70.爬楼梯(进阶)、322.零钱兑换、279.完全平方数
爬楼梯(进阶)
题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
思路:本题也可以抽象成完全背包的问题,背包就是总共多少阶台阶,物品就是每次可以爬多少楼梯,可以爬1阶也可以爬2阶,和顺序有关系,所有是完全背包
- dp[i]的含义:爬i阶楼梯,总共有dp[i]种方法
- 递推公式:dp[i] += dp[i-j]
- dp初始化:dp[0] = 1
- 遍历顺序:先遍历背包,后遍历物品
- 打印dp数组
class Solution {public int climbStairs(int n) {// dp[i]表示:爬i阶台阶有dp[i]中方式int[] dp = new int[n+1];// 初始化dp[0] = 1;int[] weigth = {1,2};for(int i = 0;i<=n;i++){// 背包for(int j = 0;j<weigth.length;j++){// 物品if(i >= weigth[j]){dp[i] += dp[i-weigth[j]];}}}return dp[n];}
}
零钱兑换
题目:给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
- dp[j]的含义:凑成金额为j,最少需要dp[j]个硬币
- 递推公式:dp[j] = Math.min(dp[j],dp[j-coins[i]]+1)
- dp[j]不放当前硬币,因为是一维数组,所有这里用的是上一次遍历的结果
- dp[j-coins[i]]+1,放当前硬币;放了当前硬币,剩余的金额的最少硬币数+1(当前这个硬币)就是放当前硬币的最少硬币数
- dp数组初始化:dp[j] = Integer_MAX_VALUE,dp[0] = 0,因为取的是最小值,所有就不能全部初始化成0了,因为dp[0] = 0,所有就会一种都是0
- 遍历顺序:先遍历物品,后遍历背包
- 打印dp数组
class Solution {public int coinChange(int[] coins, int amount) {// dp[i]表示:凑成金额为i,最少需要dp[i]个硬币int[] dp = new int[amount+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0] = 0;for(int i = 0;i<coins.length;i++){// 物品for(int j = coins[i];j<=amount;j++){// 背包if(dp[j-coins[i]] != Integer.MAX_VALUE){// 如果遇到初始值则跳过dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 :dp[amount];}
}
完全平方数
题目:给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
思路:本题的物品就是1,4,9,16…等等完全平方数,背包就是n
- dp[i]的含义:dp[i]个完全平方数和为i
- 递推公式:dp[i] = Math.min(dp[i],dp[i-i*i]+1)
- dp数组初始化:dp[i]=Integer.MAX_VALUE,dp[0]=0
- 遍历顺序:先物品,后背包
- 打印dp数组
class Solution {public int numSquares(int n) {// dp[i]表示整数i,dp[i]个完全平方数和为iint[] dp = new int[n+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0] = 0;for(int i = 1;i*i<=n;i++){// 物品for(int j = i*i;j<=n;j++){// 背包if(dp[j-i*i] != Integer.MAX_VALUE){dp[j] = Math.min(dp[j],dp[j-i*i]+1);}}}return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];}
}
相关文章:
、322.零钱兑换、279.完全平方数)
算法刷题|70.爬楼梯(进阶)、322.零钱兑换、279.完全平方数
爬楼梯(进阶) 题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 思路:本题也可以抽象成完全背包的问题,背包就是总共多少阶台阶&am…...
【MCS-51】51单片机结构原理
至今为止,MCS-51系列单片机有许多种型号的产品:其中又分为普通型51(8031、8051、89S51)和增强型52(8032、8052、89S52等)。它们最大的区别在于存储器配置各有差异。下面我举例子的都是8051这一系列的单片机…...
)
软件测试技术之如何编写测试用例(3)
14、对于类似于手机版淘宝这种软件,它拥有客户端,服务器端还有一个后台管理系统类似于进销存管理系统,我如何设计测试用例才能保证功能的完全覆盖?他们之间的交互如何设计测试用例? 专家分析:对于复合型的…...

移远通信笔试题
限时60分钟 1.下列关于栈叙述正确的是 A A) 栈顶元素最先能被删除 B)栈顶元素最后才能被删除 C)栈底元素永远不能被删除 D)以上三种都不对 在栈中,最后被压入的元素总是在栈顶上方,而栈顶元素总是最先被弹出的元…...
)
python算法中的机器学习算法之监督学习知识点(详解)
目录 学习目标: 学习内容: Ⅰ. 线性回归(Linear Regression) Ⅱ. 逻辑回归(Logistic Regression)...

Flink主要有两种基础类型的状态:keyed state
Flink主要有两种基础类型的状态:keyed state 和operator state。 Keyed State Keyed State总是和keys相关,并且只能用于KeyedStream上的函数和操作。 你可以将Keyed State视为是已经被分片或分区的Operator State,每个key都有且仅有一个状态分…...
js录音支持h5 pc ios android
最近在做h5录音的页面要求可暂停录音,继续录音,写好后发现不兼容ios,无奈只能找兼容方法,找了一天也没找到,后来看到一个网站在ios上可以暂停录音,后来引入他的js文件果然能用了 网站放下面了 Recorder H5: 用于html5网页中的前…...

mybatis04-mybatis缓存、分页插件、注解开发(一对一、多对一、多对多)
mybatis04 mybatis 缓存 一、mybatis 缓存概述 1、缓存 缓存 是存在于内存中的临时数据,使用缓存的目的是:减少和数据库的交互次数,提高执行效率。 2、mybatis 缓存 mybatis 与 大多数的持久层框架一样,提供了缓存策略…...

软件平台接口常见问题汇总
接口常见问题汇总 一、接口技术层面 1、输入参数验证校验不全面。如: 1.1入参数据类型长度边界,范围边界。 1.2 入参数据内容、成员内容,有效无效,合法非法。 1.3 入参数据 特殊字符 敏感字符过滤。 1.4 入参可否必选。 2、接口…...
SparkStreaming学习之——无状态与有状态转化、遍历kafka的topic消息、WindowOperations
目录 一、状态转化 二、kafka topic A→SparkStreaming→kafka topic B (一)rdd.foreach与rdd.foreachPartition (二)案例实操1 1.需求: 2.代码实现: 3.运行结果 (三)案例实操2 1.需求: 2.代码实现: 3.运行结果 三、W…...
)
上市公司碳排放测算数据(1992-2022年)
根据《温室气体核算体系》,企业的碳排放可以分为三个范围。 范围一是直接温室气体排放,产生于企业拥有或控制的排放源,例如企业拥有或控制的锅炉、熔炉、车辆等产生的燃烧排放;拥有或控制的工艺设备进行化工生产所产生的排放。 范…...
Springboot 整合 JPA 及 Swagger2
首先是官方文档: Spring Data JPA - Reference Documentationhttps://docs.spring.io/spring-data/jpa/docs/2.2.4.RELEASE/reference/html/#repositories.query-methods 1、JPA相关概念 2、创建 Springboot 项目 修改 pom 文件,可以直接进行复制粘贴&a…...
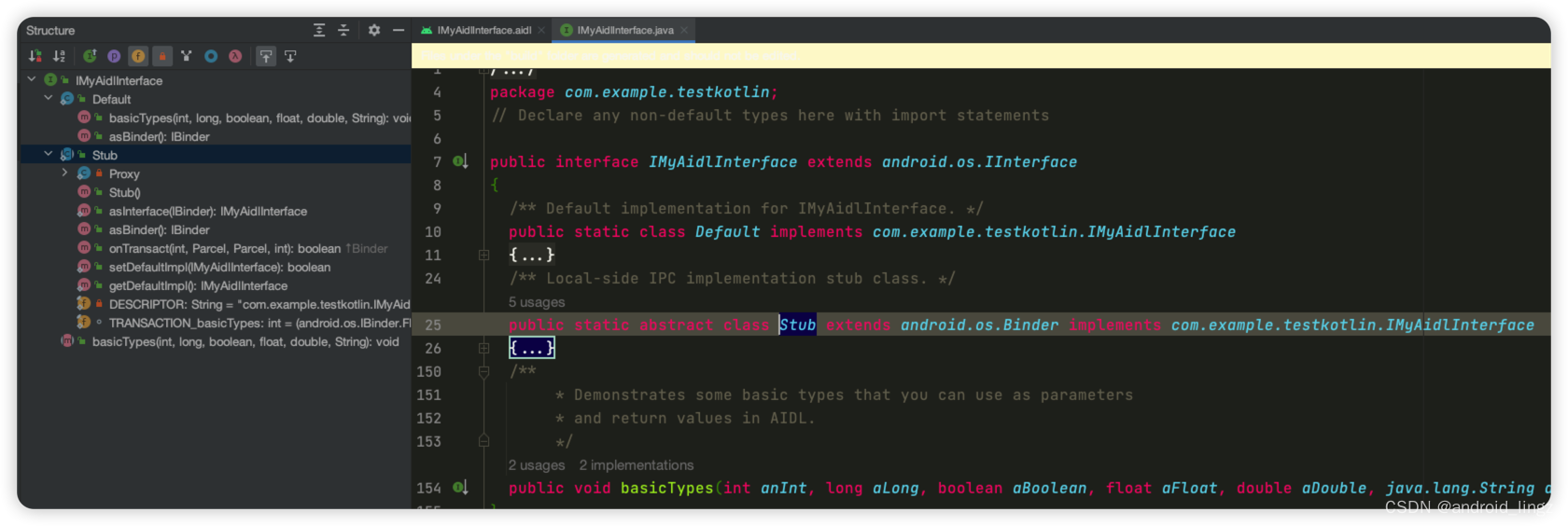
android aidl
本文只是记录个人学习aidl的实现,如需学习请参考下面两篇教程 官方文档介绍Android 接口定义语言 (AIDL) | Android 开发者 | Android Developers 本文参考文档Android进阶——AIDL详解_android aidl_Yawn__的博客-CSDN博客 AIDL定义:Android 接口…...
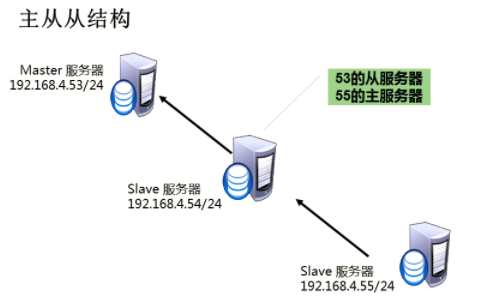
MYSQL---主从同步概述与配置
一、MYSQL主从同步概述 1、什么是MySQL主从同步? 实现数据自动同步的服务结构 主服务器(master): 接受客户端访问连接 从服务器(slave):自动同步主服务器数据 2、主从同步原理 Maste:启用binlog 日志 Slave:Slave_IO: 复制master主…...

WebClient学习
1. 介绍 Java中传统的RestTemplate 的主要问题在于不支持响应式流规范,也就无法提供非阻塞式的流式操作。而WebClient是响应式、非阻塞的客户端,属于Spring5中的spring-webflux库 2. 依赖 maven依赖 <dependency><groupId>org.springfra…...

「计算机控制系统」6. 直接设计法
特殊类型系统的最小拍无差设计 一般系统的最小拍无差设计 最小拍控制器的工程化改进 Dahlin算法 文章目录 特殊类型系统的最小拍无差设计理论分析典型输入函数的最小拍无差系统 一般系统的最小拍无差设计有波纹最小拍无差设计无波纹最小拍无差设计 最小拍控制器的工程化改进针对…...
什么是JWT?
起源 需要了解一门技术,首先从为什么产生开始说起是最好的。JWT 主要用于用户登录鉴权,所以我们从最传统的 session 认证开始说起。 session认证 众所周知,http 协议本身是无状态的协议,那就意味着当有用户向系统使用账户名称和…...

STM32—0.96寸OLED液晶显示
本文主要介绍基于STM32F103的0.96寸的OLED液晶显示,详细关于0.96寸OLED液晶屏幕的介绍可参考这篇博客:https://blog.csdn.net/u011816009/article/details/130119426 一、简介 OLED被称为有机激光二极管,也被称为有机激光显示,O…...

Mysql的简介和选择
文章目录 前言一、为什么要使用数据库 数据库的概念为什么要使用数据库二、程序员为什么要学习数据库三、数据库的选择 主流数据库简介使用MySQL的优势版本选择四、Windows 平台下安装与配置MySQL 启动MySQL 服务控制台登录MySQL命令五、Linux 平台下安装与配置MySQL总结 前言…...

3D视觉之深度相机方案
随着机器视觉,自动驾驶等颠覆性的技术逐步发展,采用 3D 相机进行物体识别,行为识别,场景 建模的相关应用越来越多,可以说 3D 相机就是终端和机器人的眼睛。 3D 相机 3D 相机又称之为深度相机,顾名思义&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
