Python算法设计 - 编码加密
一、编码加密
编码加密应用十分广泛,特别是在大数据时代,也因此信息安全变得尤为重要
有时我会读到“OTP是一种无法被破解的加密方式”,当然,文末会附上一个完全被破解的OTP加密的例子
问题在于,人们经常会觉得完美的加密方式就是不可破解的加密方式,如果密码是完美的(根据香农定理),则从不同的明文获得密文实例的概率分布必须是均匀的,换句话说,给定一些密码文本,任何纯文本都有相同的机会成为源
这样的话,即使是计算能力再厉害的对手也无法从纯密码文本中获取任何关于纯文本的信息
但这远不是牢不可破的,即使正确的使用OTP也很容易损坏,设想一家银行用OTP对数字支票进行加密,在众所周知的支票处重写100.0美元-999.99美元有多容易?
OTP是完美的密码?其实在大多数实现方式下不是的。当人们强调密钥的单一使用时,他们也会忘了密钥分配的一致性,这往往也是非常重要的
当我生成信息的时候,我违反了一次性规则,那么后果是不可避免的
二、Python算法实现
ciphertext = [b'm\x99QH\xfc\x99\xcel\xfc>\x11\xf81\xda:\x15"6\xd3b\x07\x7f\xed\x87\xd5\xd4\xf0\xbb',b'x\x96^\r\xb5\x83\x86u\xeel\x0e\xf8,\xce:\x06 6\xd0b\nx\xfd\x87\xd9\xc9\xe8',b'm\x90O^\xfc\x80\xd3f\xe7>\x16\xf46\x89w\x05r8\xcb-\x04',b'`\x97O\r\xbd\x9f\xc3%\xe1q\x0e\xb15\xdbu\x0e5y\xca*\x1c7\xec\xc2\xd2\xcb',b"m\x90[Y\xfc\x80\xdf%\xeb\x7f\x03\xe2b\xc1{\x167y\xdf'\x16y\xa8\xc6\x97\xc2\xed\xa9p(",b'`\x9dN\r\xb5\x8b\x86m\xe0n\x1f\xb1*\xc8i@45\xd25\x1d7\xe9\xd0\xd6\xdf',b'p\x96\x1aL\xfc\x83\xcfb\xe7jZ\xfe0\x89s\x0er8\x9d&\x12n',b'p\x96\x1aL\xfc\x9b\xcfv\xe6q\x14\xb1-\xdb:\t<y\xd3-\x1dr',b'p\x8b\x1aD\xa8\xcd\xd2m\xeal\x1f\xf7-\xdb\x7f@&1\xd8b\x1fr\xfb\xd4\x97\xc1\xf0\xa2t',b'x\x94V\r\xa8\x85\xc7q\xafi\x1f\xb11\xcc\x7f@=+\x9d1\x16r\xe5',b'p\x8b\x1aO\xa9\x99\x86d\xafz\x08\xf4#\xc4:\x17;-\xd5+\x1d7\xe9\x87\xd3\xd4\xfa\xad|',b'p\xd8IY\xbd\x83\xc2%\xees\x13\xf5b\xddr\x05r+\xd2#\x01',b'v\x9e\x1aL\xfc\x9e\xd3w\xe9>\x0e\xfe0\xc4\x7f\x0e&<\xd9b\x00\x7f\xe7\xd5\xd2',b'x\x96^\r\x95\xcd\xcej\xe3zZ\xe6+\xddr\t<y\xd0;S\x7f\xe9\xc9\xd3',b"~\x8a[D\xb2\x9e\x86j\xe9>\x0e\xf9'\x89}\x0f>=\xd8,Sd\xe9\xc9\xd3",b'q\x97M\r\xba\x88\xd1%\xf6{\x0e\xb1*\xc6m@&1\xd8;St\xfa\xc2\xd2\xd6',b'm\x90HB\xa9\x8a\xce%\xe2gZ\xf7+\xc7}\x05 *\x9d6\x1c7\xfc\xcf\xd2\x86\xfb\xa9t5',b'n\x90SA\xb9\xcd\xcf%\xf8{\x1f\xe1b\xder\t><\x9d\x0bS`\xed\xc2\xc7',b'9\xd8_I\xbb\x8c\xd4%\xeer\x16\xf0,\x89j\x0f7y\x9dbS7\xa8\x87\x97\x86\xbf',
]from string import ascii_lowercase #ASCII字符# 允许字符集
letters = set(ascii_lowercase + ' ')# 重构消息
plaintext = [''] * len(ciphertext)# 把所有代码放在同一位置
for messages in zip(*ciphertext):keys = set()# 找到可行密钥for key in range(256):for m in messages:if chr(m ^ key) not in letters:breakelse:keys.add(key)key = keys.pop() if len(keys) == 1 else None# 重构明文for i, m in enumerate(messages):if key is not None:plaintext[i] += chr(m ^ key)else:plaintext[i] += '?'print(plaintext)
- chr(i)函数返回整数i对应的ASCII字符,与ord()作用相反,参数取值范围[0,255]之间的正数。该函数在python2和python3各个版本中都可用。不存在兼容性问题
- key = keys.pop() if len(keys) == 1 else None是Python中高级且高效的写法,也可写成:
if len(keys) == 1:key = keys.pop()
else:key = None
类似于 x**2 for x in range(10),那么这种写法也可写为:
def multi(x):for x in range(10):x = x**2
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出元素下标和元素,一般用在 for 循环当中。
相关文章:

Python算法设计 - 编码加密
一、编码加密 编码加密应用十分广泛,特别是在大数据时代,也因此信息安全变得尤为重要 有时我会读到“OTP是一种无法被破解的加密方式”,当然,文末会附上一个完全被破解的OTP加密的例子 问题在于,人们经常会觉得完美的…...
数据结构和算法学习记录——平衡二叉树(基本介绍、平衡因子、平衡二叉树的定义、平衡二叉树的高度)
目录 基本介绍 平衡因子 平衡二叉树 平衡二叉树的高度 基本介绍 什么是平衡二叉树? 以一个例子来解释一下: 搜索树结点按不同的插入次序,将会导致不同的深度和平均查找长度ASL 在二叉搜索树中查找一个元素: (…...
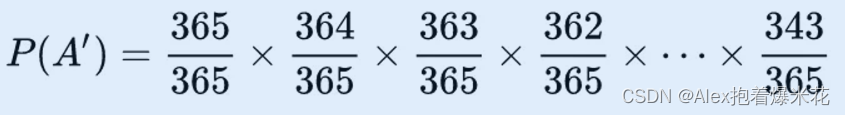
【浓缩概率】浓缩概率思想帮我蒙选择题的概率大大提升!
今天在学习的时候遇到一个很有趣的思想叫作浓缩概率,可以帮我们快速解决一下概率悖论问题! 什么是概率 计算概率有下面两个最简单的原则: 原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现…...
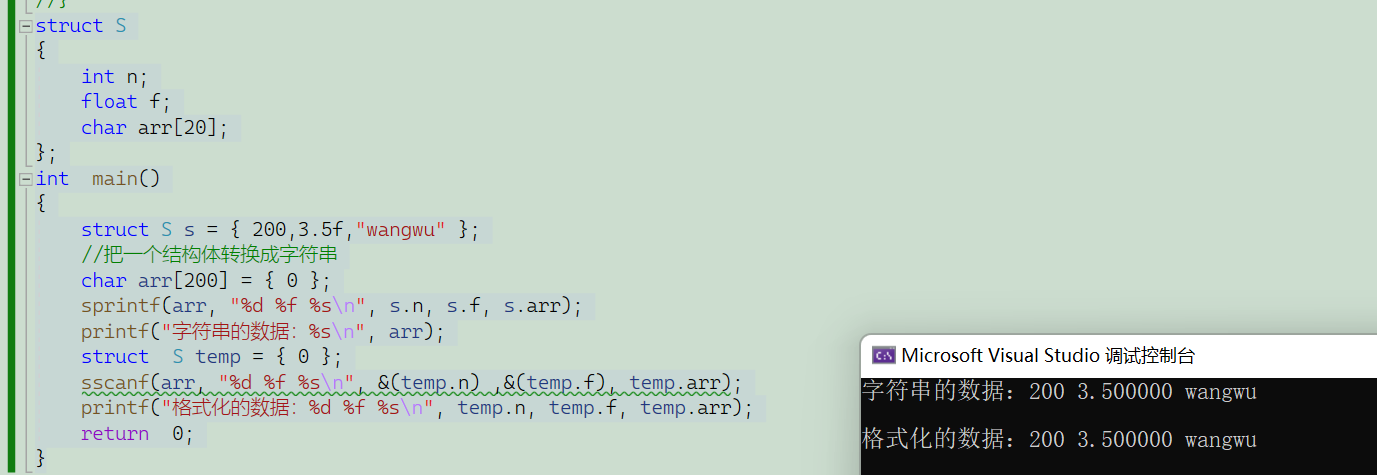
两小时让你全方位的认识文件(一)
想必友友们在生活中经常会使用到各种各样的文件,那么我们是否了解它其中的奥秘呢,今天阿博就带领友友们深入地走入文件🛩️🛩️🛩️ 文章目录 一.为什么使用文件二.什么是文件三.文件的打开和关闭四.文件的顺序读写 一…...

基于Java+Springboot+vue网上商品订单转手系统设计和实现
基于JavaSpringbootvue网上商品订单转手系统设计和实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式…...

旅游-商场购物
标题 前言必学场景词汇及用法售货员接待促销活动选购商品询问材质与质量试穿衣服杀价修改衣服结账售后服务退换货情境常用单词化妆品类别护肤品类别护肤品功能前言 加油 必学场景词汇及用法 售货员接待 1.be of service to sb 服务某人 Hello, ma’am. Could I be of serv…...

毕业论文用什么流程图软件比较好?
在写作论文的时候使用流程图,会让我们的论文看起来更加有逻辑。并且流程图的图片都可以在PPT中随意插入以及使用。 基础流程图作为最为基本和简单的的流程图方式,一般不区分用户角色和场景,适用于简单场景,梳理单一的流程情况&am…...
、322.零钱兑换、279.完全平方数)
算法刷题|70.爬楼梯(进阶)、322.零钱兑换、279.完全平方数
爬楼梯(进阶) 题目:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 思路:本题也可以抽象成完全背包的问题,背包就是总共多少阶台阶&am…...
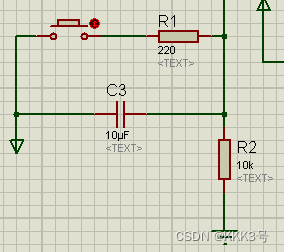
【MCS-51】51单片机结构原理
至今为止,MCS-51系列单片机有许多种型号的产品:其中又分为普通型51(8031、8051、89S51)和增强型52(8032、8052、89S52等)。它们最大的区别在于存储器配置各有差异。下面我举例子的都是8051这一系列的单片机…...
)
软件测试技术之如何编写测试用例(3)
14、对于类似于手机版淘宝这种软件,它拥有客户端,服务器端还有一个后台管理系统类似于进销存管理系统,我如何设计测试用例才能保证功能的完全覆盖?他们之间的交互如何设计测试用例? 专家分析:对于复合型的…...

移远通信笔试题
限时60分钟 1.下列关于栈叙述正确的是 A A) 栈顶元素最先能被删除 B)栈顶元素最后才能被删除 C)栈底元素永远不能被删除 D)以上三种都不对 在栈中,最后被压入的元素总是在栈顶上方,而栈顶元素总是最先被弹出的元…...
)
python算法中的机器学习算法之监督学习知识点(详解)
目录 学习目标: 学习内容: Ⅰ. 线性回归(Linear Regression) Ⅱ. 逻辑回归(Logistic Regression)...

Flink主要有两种基础类型的状态:keyed state
Flink主要有两种基础类型的状态:keyed state 和operator state。 Keyed State Keyed State总是和keys相关,并且只能用于KeyedStream上的函数和操作。 你可以将Keyed State视为是已经被分片或分区的Operator State,每个key都有且仅有一个状态分…...
js录音支持h5 pc ios android
最近在做h5录音的页面要求可暂停录音,继续录音,写好后发现不兼容ios,无奈只能找兼容方法,找了一天也没找到,后来看到一个网站在ios上可以暂停录音,后来引入他的js文件果然能用了 网站放下面了 Recorder H5: 用于html5网页中的前…...

mybatis04-mybatis缓存、分页插件、注解开发(一对一、多对一、多对多)
mybatis04 mybatis 缓存 一、mybatis 缓存概述 1、缓存 缓存 是存在于内存中的临时数据,使用缓存的目的是:减少和数据库的交互次数,提高执行效率。 2、mybatis 缓存 mybatis 与 大多数的持久层框架一样,提供了缓存策略…...

软件平台接口常见问题汇总
接口常见问题汇总 一、接口技术层面 1、输入参数验证校验不全面。如: 1.1入参数据类型长度边界,范围边界。 1.2 入参数据内容、成员内容,有效无效,合法非法。 1.3 入参数据 特殊字符 敏感字符过滤。 1.4 入参可否必选。 2、接口…...
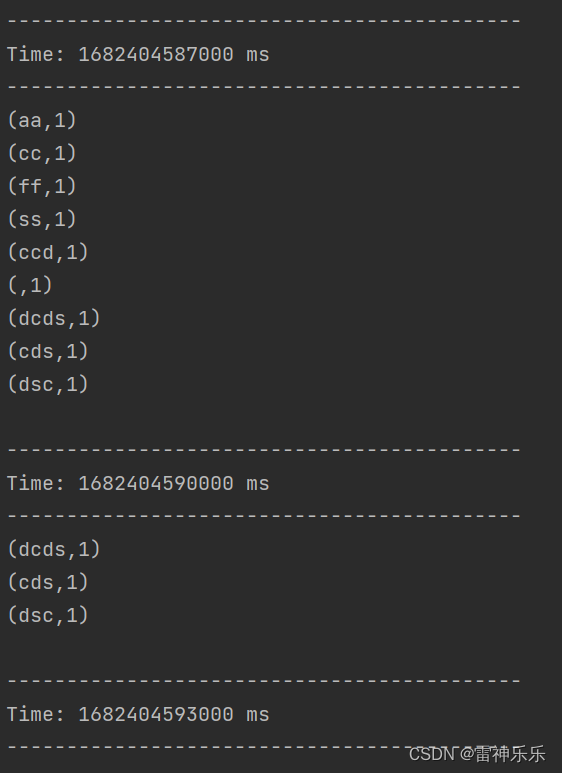
SparkStreaming学习之——无状态与有状态转化、遍历kafka的topic消息、WindowOperations
目录 一、状态转化 二、kafka topic A→SparkStreaming→kafka topic B (一)rdd.foreach与rdd.foreachPartition (二)案例实操1 1.需求: 2.代码实现: 3.运行结果 (三)案例实操2 1.需求: 2.代码实现: 3.运行结果 三、W…...
)
上市公司碳排放测算数据(1992-2022年)
根据《温室气体核算体系》,企业的碳排放可以分为三个范围。 范围一是直接温室气体排放,产生于企业拥有或控制的排放源,例如企业拥有或控制的锅炉、熔炉、车辆等产生的燃烧排放;拥有或控制的工艺设备进行化工生产所产生的排放。 范…...
Springboot 整合 JPA 及 Swagger2
首先是官方文档: Spring Data JPA - Reference Documentationhttps://docs.spring.io/spring-data/jpa/docs/2.2.4.RELEASE/reference/html/#repositories.query-methods 1、JPA相关概念 2、创建 Springboot 项目 修改 pom 文件,可以直接进行复制粘贴&a…...
android aidl
本文只是记录个人学习aidl的实现,如需学习请参考下面两篇教程 官方文档介绍Android 接口定义语言 (AIDL) | Android 开发者 | Android Developers 本文参考文档Android进阶——AIDL详解_android aidl_Yawn__的博客-CSDN博客 AIDL定义:Android 接口…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
