【故障检测】基于 KPCA 的故障检测【T2 和 Q 统计指数的可视化】（Matlab代码实现）

💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥


🏆 博主优势： 🌞 🌞 🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

📋 📋 📋 本文目录如下： 🎁 🎁 🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现

💥1 概述

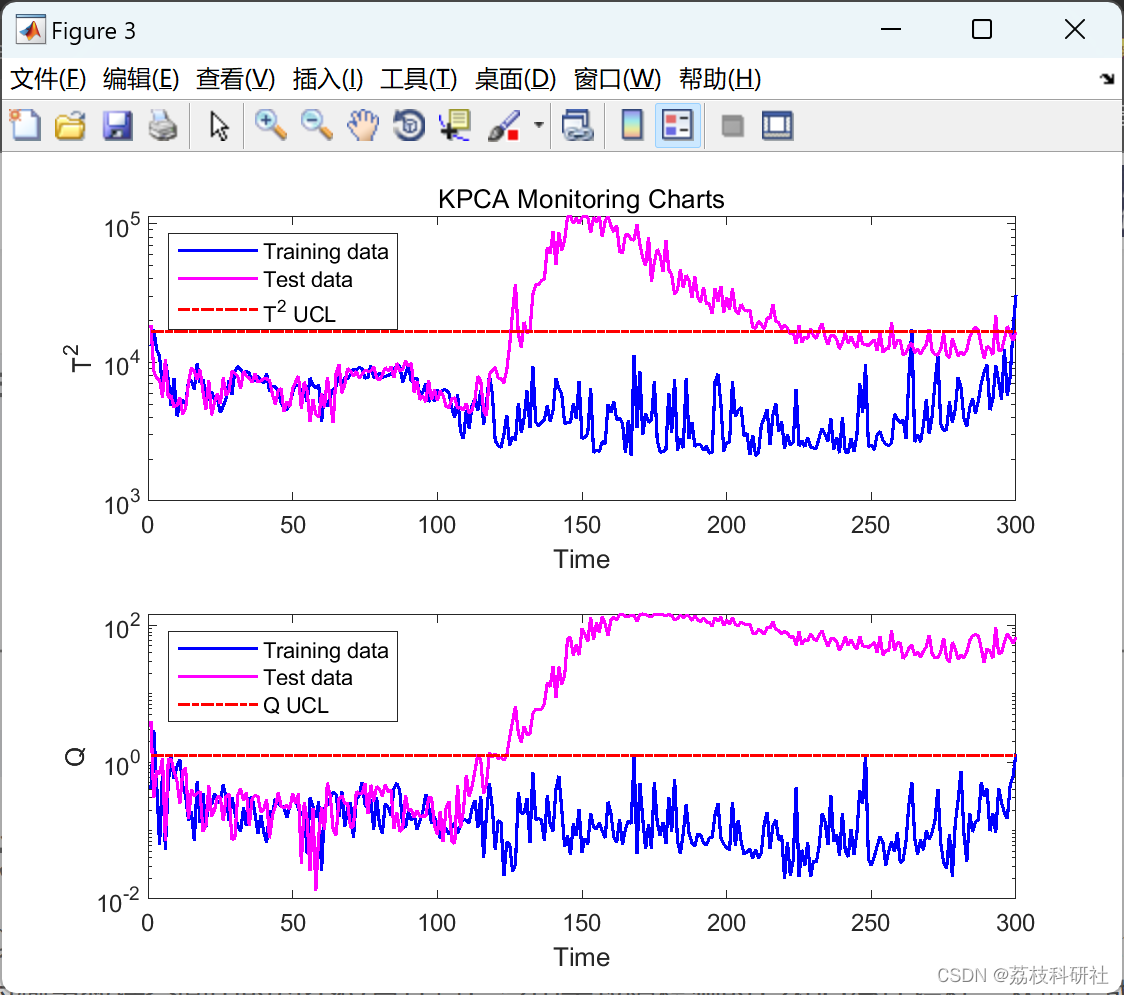
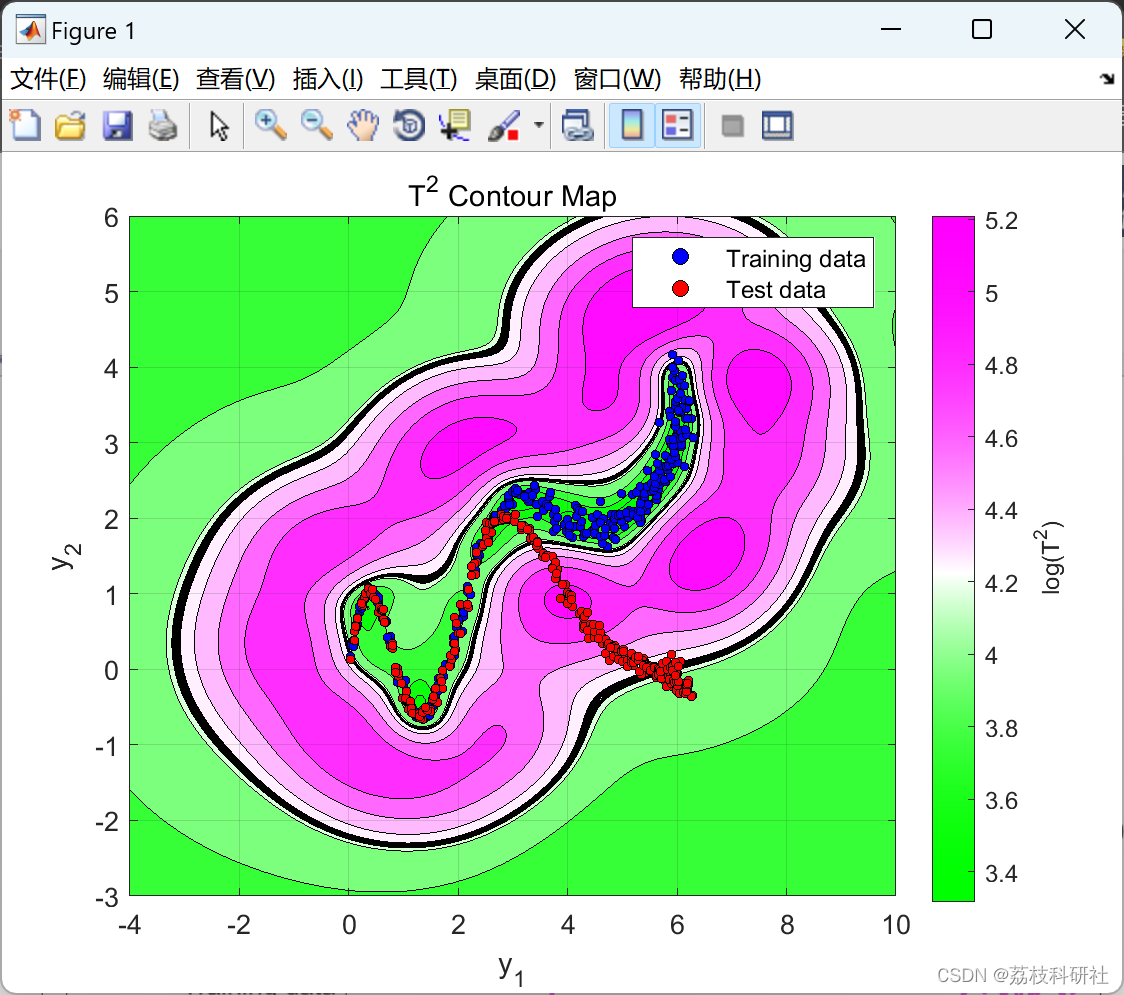
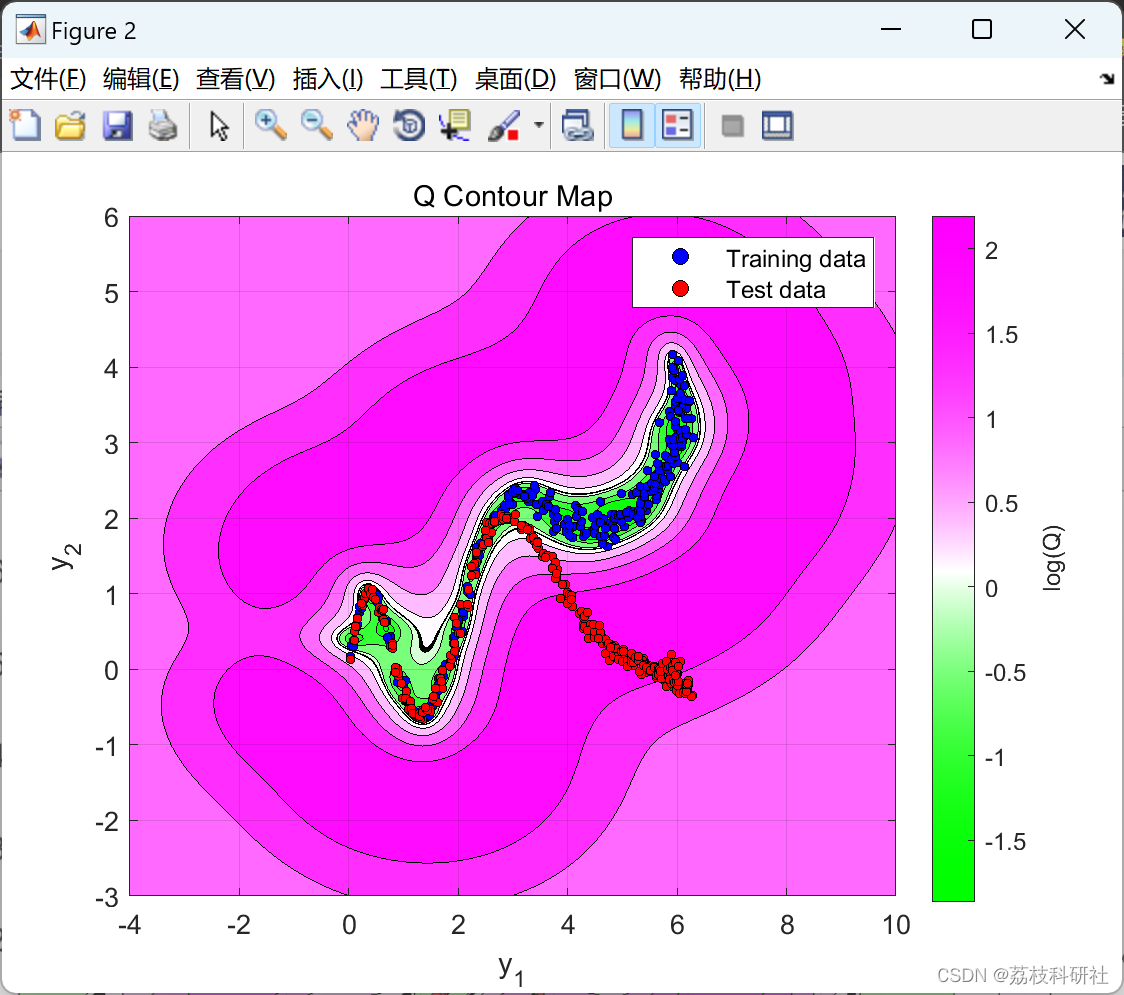
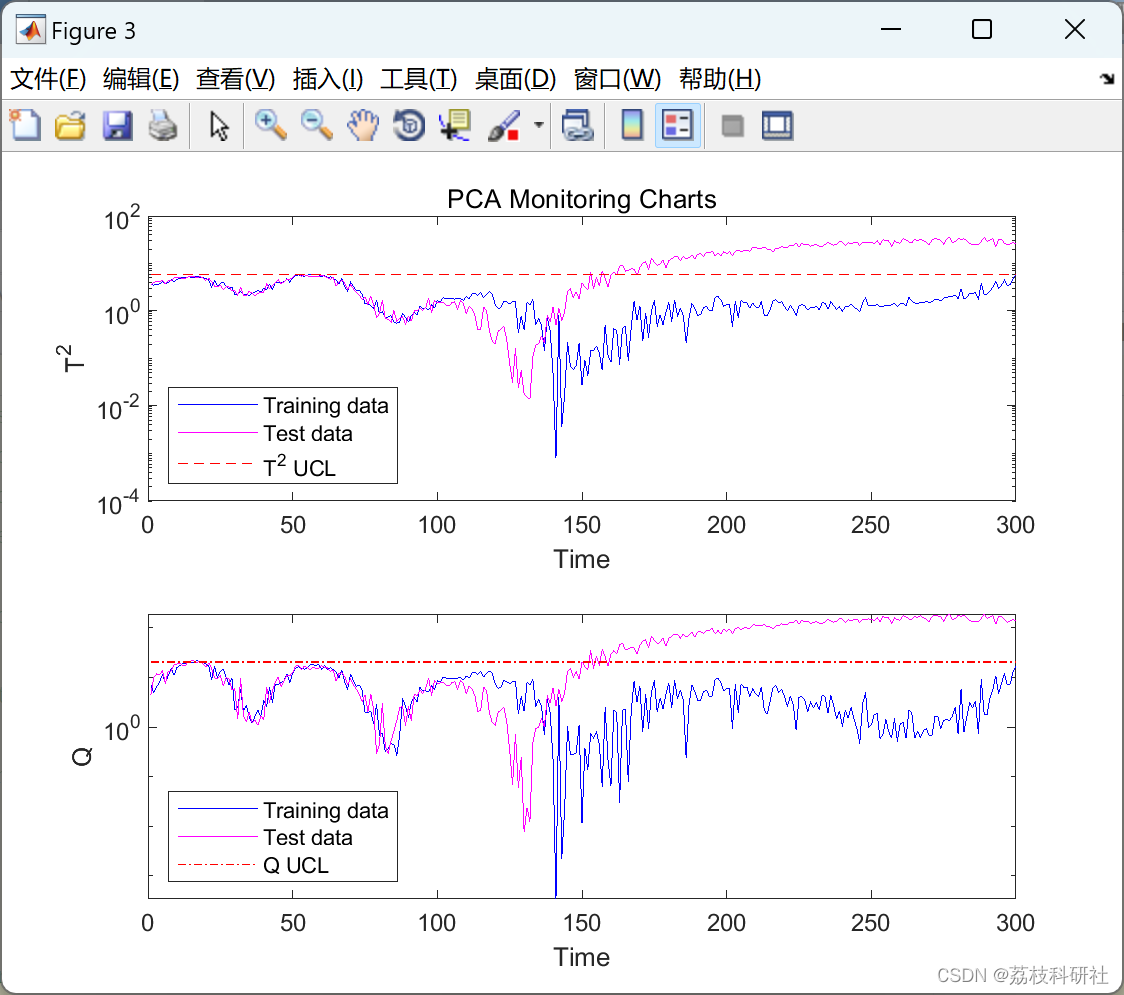
数据包含取自模拟流程示例的二维数据集。此数据用于训练和测试内核 PCA 以进行故障检测。训练后，针对输出数据空间中的每个位置计算广泛用于故障检测的T2和Q统计指标，从而生成等高线图。然后将 2% 显著性水平检测限叠加在地图上，作为数据空间的正常（绿色）和错误（洋红色）区域之间的边界。

使用等高线图，可以将各种核类型和参数选择对正常和错误过程状态之间的决策边界的影响可视化。

📚2 运行结果

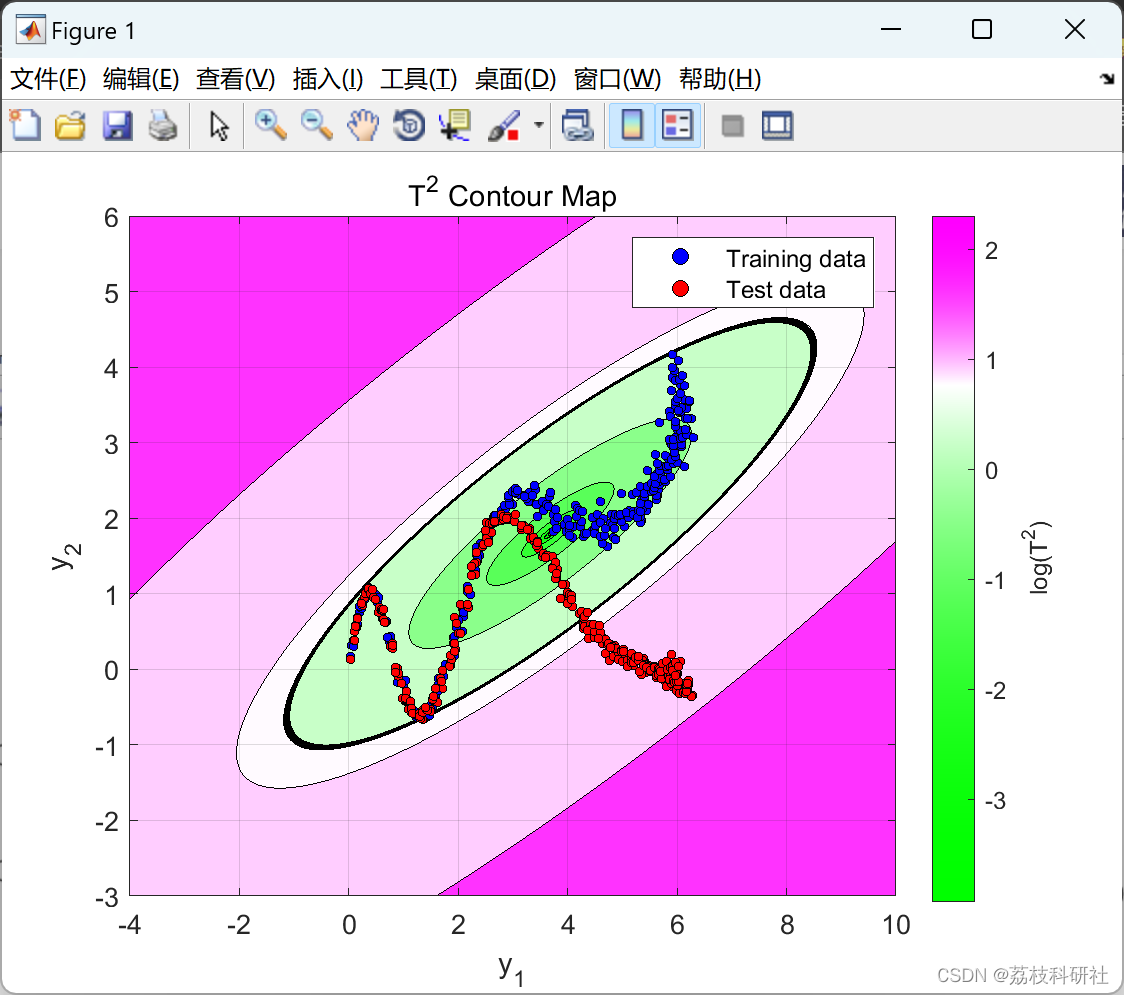
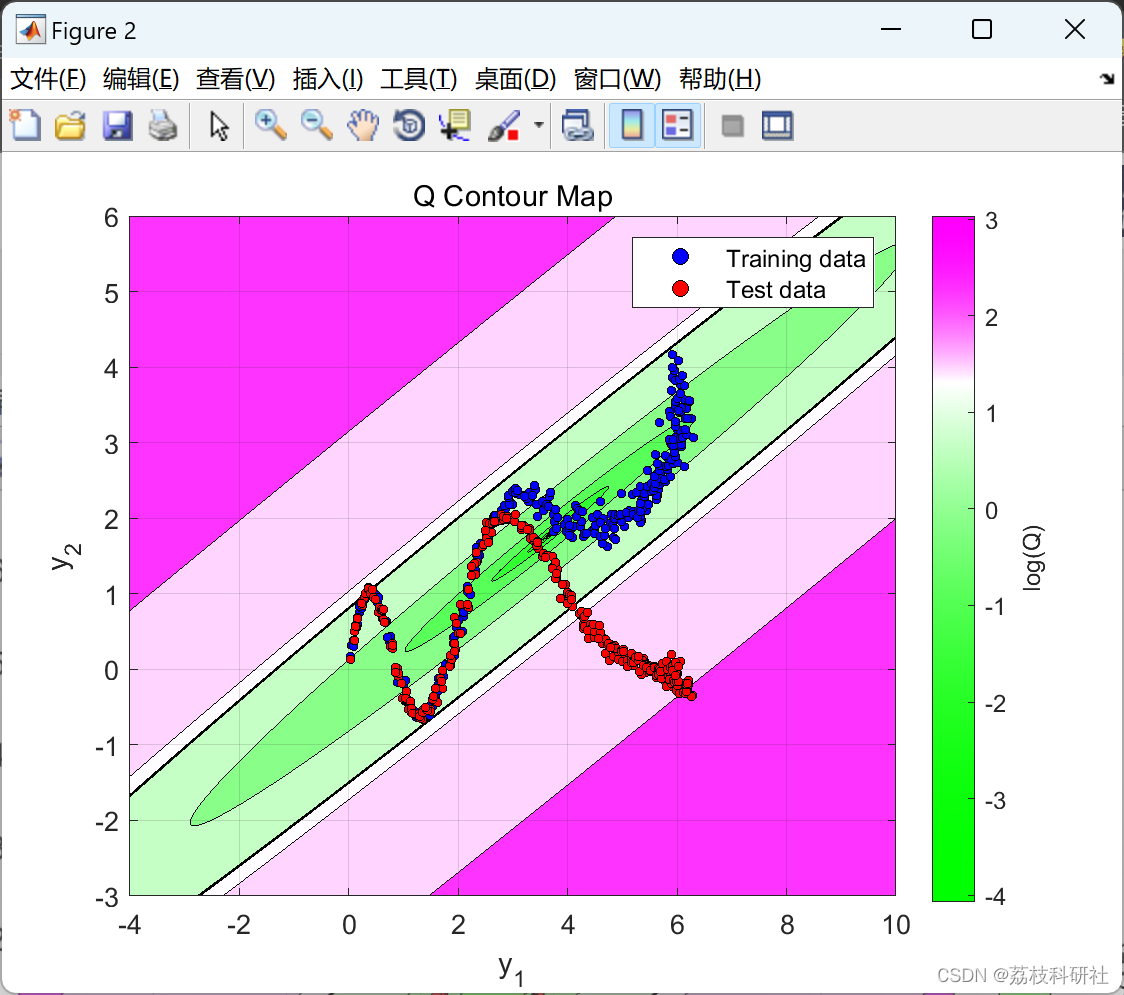
部分代码：

%% Get 2D data

close all; clc; tic;

if nargin == 0

load dataset.mat p;

train = p{1}; test = p{2};

% Kernel types and parameters:

ktype = 'rbf'; kpar = 1; % RBF kernel

%ktype = 'rbf'; kpar = 10; % RBF kernel

%ktype = 'rbf'; kpar = 0.9; % RBF kernel

%ktype = 'rbfpoly'; kpar = [1 1 0.65]; % mixed kernel

%ktype = 'poly'; kpar = 2; % polynomial kernel

%ktype = 'imquad'; kpar = 10; % inverse multiquadric kernel

%ktype = 'cauchy'; kpar = 5; % Cauchy kernel

end

%lax = [-15 15 -15 15];

lax = [-4 10 -3 6]; % Axes limits

N = length(train); M = length(test);

z0T = train; z1T = test; % Training and Test data

[xx,yy] = meshgrid(lax(1):0.05:lax(2),... % Meshgrid for contours

lax(3):0.05:lax(4));

z2T = [xx(:) yy(:)]; L = length(z2T); % Vectorize meshgrid points

K.type = ktype; K.p = kpar; % Kernel type and parameters

set(0,'defaultfigurecolor',[1 1 1]); % Set fig color to w

conf = 0.99; % Significance level (*100%)

% Normalize 2D Data

zm = mean(z0T); zs = std(z0T);

z0 = (z0T - zm(ones(N,1),:))./zs(ones(N,1),:); % Normalize training z

z1 = (z1T - zm(ones(N,1),:))./zs(ones(M,1),:); % Normalize test z

z2 = (z2T - zm(ones(L,1),:))./zs(ones(L,1),:); % Normalize surf z

%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% KERNEL PRINCIPAL COMPONENTS ANALYSIS %

[K0c,K0,U0] = kerneltrain(z0,K); % Populate kernel matrix

K1c = kerneltest(z1,z0,K0,U0,K); % Project test data to RKHS

K2c = kerneltest(z2,z0,K0,U0,K); % Project surf data to RKHS

[V,D] = eig(K0c/N); % Eigenvalue decomposition

[S,sj] = sort(diag(D),'descend'); % Sort eigenvalues

V = V(:,sj); S = S'; % Re-arrange eigenvectors

S(S < 1e-7) = []; % Remove eigenvalues <= 0

P = V(:,1:length(S))*diag(S.^-0.5); % Projection matrix

if ~isreal(S)

disp('Complex eigenvalues detected.'); % Warn about complex eigs

end

%% Perform KPCA Monitoring

CS = cumsum(S)/sum(S)*100;

RP = find(CS >= 99.9,1); % Get eigenvalues by %CPV

disp([num2str(RP) ' principal'...

' components chosen.']);

t0 = K0c*P(:,1:RP); % Kernel subspace (train)

t1 = K1c*P(:,1:RP); % Kernel subspace (test)

t2 = K2c*P(:,1:RP); % Kernel subspace (surf)

T2 = sum((t0.^2)./S(ones(N,1),1:RP),2); % T2 statistics (train)

t0n = K0c*P; % Full kernel space

Q = abs(sum(t0n.^2,2) - sum(t0.^2,2)); % Q statistics (train)

if strcmp(ktype,'rbf') == 1

fprintf('\n At infinite fault magnitude:\n');

U1 = ones(1,N)/N;

tt = U1*K0*(U0 - eye(N))*P(:,1:RP);

fprintf(' T2 limit: %.2f\n',...

sum((tt.^2)./S(1:RP),2)); % Limit of T2 for RBF

tu = U1*K0*(U0 - eye(N))*P;

fprintf(' Q limit: %.2f\n\n',...

abs(sum(tu.^2,2) - sum(tt.^2,2))); % Limit of Q for RBF

end

T2t = sum((t1.^2)./S(ones(M,1),1:RP),2); % T2 statistics (test)

T2u = sum((t2.^2)./S(ones(L,1),1:RP),2); % T2 statistics (surf)

t1n = K1c*P; t2n = K2c*P;

Qt = abs(sum(t1n.^2,2) - sum(t1.^2,2)); % Q statistics (test)

Qu = abs(sum(t2n.^2,2) - sum(t2.^2,2)); % Q statistics (surf)

%% Plot monitoring charts

figure(3); subplot(211);

semilogy(1:N,T2,'b',1:M,T2t,'m','linewidth',1.2); % T2 monitoring chart

xlabel('Time'); ylabel('T^2'); subplot(212);

semilogy(1:N,Q,'b',1:M,Qt,'m','linewidth',1.2); % Q monitoring chart

xlabel('Time'); ylabel('Q');

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] K.E.S. Pilario, Y. Cao, and M. Shafiee. Mixed Kernel Canonical Variate Dissimilarity Analysis for Incipient Fault Monitoring in Nonlinear Dynamic Processes. Comput. and Chem. Eng., 123, 143-154. 2019. doi: 10.1016/j.compchemeng.2018.12.027

🌈4 Matlab代码实现