[NSSRound#11] 密码学个人赛
这个比赛没有参加,跟别人要了些数据跑一下,其实交互这东西基本上一样,跑通就行.
ez_enc
这题有点骗人,给了一堆AB串,一开始以为是培根密码,结果出来很乱.再看长度:192 应该就是01替换
a = 'ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAAABBAABBBABABABAAAABBAAABABAABABBABBBABBAAABBBAABABAABBAAAABBBAAAABAABBBAABBABABAABABAAAAABBBBABAABBBBAAAABBBBBAB'
long_to_bytes(int(a.replace('A','0').replace('B','1'),2))
#NSSCTF{mS4gT1Kv9L8NjPzx}ez_fac
从名字可以看出来这是个分解题,关于RSA大数分解有好多论文,没见过的估计打死也作不出来,毕竟不是数学家.
from Crypto.Util.number import *
import random
from secret import flag,a0,a1,b0,b1p = getPrime(512)
q = getPrime(512)
e = getPrime(128)
n = p*q
assert pow(a0,2) + e * pow(b0,2) == n
assert pow(a1,2) + e * pow(b1,2) == n
m = bytes_to_long(flag)
c = pow(m,e,n)print("c=",c)
print("n=",n)
print("a0=",a0)
print("a1=",a1)
print("b0=",b0)
print("b1=",b1)
这个论文好像不很新,关于
可以得到 p = gcd(N,a0*b1-a1*b0)
c= 34007465638566836660852768374211870538357285529060206826620688555044780516477877596651414637089490522614456532732711803500304737160162560168303462221485961593760966240770414498297915175227814336224871400766371471776600674705757656616409870237891336752248110367865552469248343708419900511716030176178698949179
n= 70043427687738872803871163276488213173780425282753969243938124727004843810522473265066937344440899712569316720945145873584064860810161865485251816597432836666987134938760506657782143983431621481190009008491725207321741725979791393566155990005404328775785526238494554357279069151540867533082875900530405903003
a0= 8369195163678456889416121467476480674288621867182572824570660596055739410903686466334448920102666056798356927389728982948229326705483052970212882852055482
a1= 8369195163678456889416121462308686152524805984209312455308229689034789710117101859597220211456125364647704791637845189120538925088375209397006380815921158
b0= 25500181489306553053743739056022091355379036380919737553326529889338409847082228856006303427136881468093863020843230477979
b1= 31448594528370020763962343185054872105044827103889010592635556324009793301024988530934510929565983517651356856506719032859from gmpy2 import *e = (n - a0*a0)//b0//b0
#e = 255348562315891975282864504628198394319
'''
当 N = m*a^2 + n*b^2 时有 p = gcd(N, a0*b1 - a1*b0)
'''
p = gcd(n, a0*b1 - a1*b0)
d = invert(e, (p-1)*(n//p-1))
m = pow(c,d,n)
long_to_bytes(m)
#NSSCTF{ee7f5bf0-13b9-4a61-9b1b-243f2edef2e8}ez_signin
这题有两个点,一个是二项式定理,一个是rabin加密
from Crypto.Util.number import *
from secret import flagp = getPrime(512)
q = getPrime(512)
assert p > q
n = p*q
e = 65536
m = bytes_to_long(flag)
num1 = (pow(p,e,n)-pow(q,e,n)) % n
num2 = pow(p-q,e,n)
c = pow(m,e,n)print("num1=",num1)
print("num2=",num2)
print("n=",n)
print("c=",c)
题目给出 num1 = p^e -q^e %n ; num2 = (p-q)^e %n
二式可转化为p^e + q^e %n 中间项同时带pq被模掉.所以两式相加与n取gcd可以得到p
第二步由于 e=0x1000 是个rabin加密 ,这个直接用个模板
num1= 134186458247304184975418956047750205959249518467116558944535042073046353646812210914711656218265319503240074967140027248278994209294869476247136854741631971975560846483033205230015783696055443897579440474585892990793595602095853960468928457703619205343030230201261058516219352855127626321847429189498666288452
num2= 142252615203395148320392930915384149783801592719030740337592034613073131106036364733480644482188684184951026866672011061092572389846929838149296357261088256882232316029199097203257003822750826537629358422813658558008420810100860520289261141533787464661186681371090873356089237613080052677646446751824502044253
n= 154128165952806886790805410291540694477027958542517309121222164274741570806324940112942356615458298064007096476638232940977238598879453357856259085001745763666030177657087772721079761302637352680091939676709372354103177660093164629417313468356185431895723026835950366030712541994019375251534778666996491342313
c= 9061020000447780498751583220055526057707259079063266050917693522289697419950637286020502996753375864826169562714946009146452528404466989211057548905704856329650955828939737304126685040898740775635547039660982064419976700425595503919207903099686497044429265908046033565745195837408532764433870408185128447965
e = 65536'''
n1 = p^e - q^e
n2 = (p-q)^e = p^e + q^e
n1+n2 | n
'''
from gmpy2 import *p = gcd(num1+num2,n)
q = n//p
phi = (p-1)*(q-1)#e = 0x1000 rabin
x0=invert(p,q)
x1=invert(q,p)
cs = [c]
for i in range(16):ms = []for c2 in cs:r = pow(c2, (p + 1) // 4, p)s = pow(c2, (q + 1) // 4, q)x = (r * x1 * q + s * x0 * p) % ny = (r * x1 * q - s * x0 * p) % nif x not in ms:ms.append(x)if n - x not in ms:ms.append(n - x)if y not in ms:ms.append(y)if n - y not in ms:ms.append(n - y)cs = msfor m in ms:flag = long_to_bytes(m)if b'nss' in flag:print(flag)#nssctf{W3lc0me_t0_nssctf_R0undll_w15h_U_can_have_Fun_t0day!!!#0919}
myGame
这个题应该放前边,内容很简单,有两个菜单项,一个是加密一个是读flag,加密用相同的n和flag但是用不同的e,这样就是个很标准的共模攻击
from Crypto.Util.number import *
import os
import random
import stringflag = os.getenv('FLAG')def menu():print('''=---menu---=
1. Guess
2. Encrypt
''')p = getPrime(512)
q = getPrime(512)
n = p*qdef randommsg():return ''.join(random.choices(string.ascii_lowercase+string.digits, k=30))mymsg = randommsg()
def guess():global mymsgmsg = input()if msg == mymsg:print(flag)else:print(mymsg)mymsg = randommsg()def encrypt():e = random.getrandbits(8)c = pow(bytes_to_long(mymsg.encode()), e, n)print(f'Cipher_{e}: {c}')def main():print(f'n: {n}')while True:opt = int(input())if opt == 1:guess()elif opt == 2:encrypt()main()
由于没有远端没有数据,就直接把板子放上,应该问题不大
n,e1,e2,c1,c2 = ...g, x1, x2 = gcdext(e1,e2) #e1,e2不互素时,最后公约数g开根号,一般如果m不是很大可直接开
m = pow(c1,x1,n)*pow(c2,x2,n) % n
print(long_to_bytes(int(irrot(m,g)[0])))
myMessage
同样是没有远端,也同样是板子题,e=127 每次的n不同,取e组数据求crt然后开根号.
from Crypto.Util.number import *
import osflag = os.getenv('FLAG')e = 127def sign():msg = input("Input message:")p = getPrime(512)q = getPrime(512)n = p*qc = pow(bytes_to_long((msg + flag).encode()), e, n)print(f"n: {n}")print(f"Token: {hex(c)}")def main():while True:sign()main()举个栗子
#sage
def get_nc():...return n,c for i in range(e):tn,tc = get_nc()ns.append(tn)tc.append(tc)m127 = crt(c,n)
m = iroot(m127,e)[0]
print(long_to_bytes(int(m)))
NTR
最后一题同样是板子题,只是参数没有按原来的命名
import gmpy2
from flag import flag
from Crypto.Util.number import *def init():p = getPrime(2048)while True:x = getRandomNBitInteger(1024)y = getPrime(768)z = gmpy2.invert(x, p) * y % preturn (p, x, y, z)def encrypt(cipher, p, z):message = bytes_to_long(cipher)r = getRandomNBitInteger(1024)c = (r * z + message) % preturn cp, x, y, z = init()
c = encrypt(flag, p, z)
with open("cipher.txt", "w") as f:f.write("binz = " + str(bin(z)) + "\n")f.write("binp = " + str(bin(p)) + "\n")f.write("binc = " + str(bin(c)) + "\n")
这里定义了两个式子:
c = r*z +m (mod p)
z = y * x^-1 (mod p)
跟原行NTRU的式子: c = r*h + m (mod p) 几乎一样,只需要改下xy
#---------- NTRU -------------
binz = 0b10000100100000110000100001011001100110110111111110101001011100111001101101100100010010100110111010000001000001100011111011011000110000000111011100100010010001100110101001001110011000110000100101111001101010000101001101010001111001110000010100011001101010111000110111011111100101100100101100111000101011111101111011000101000100000010100100000110000001011100011100010001101001100101100100000101101101001100110100100101110000011001000000000010100010100011001100110101011000010000001111100101001001110111000110010001101111111110000111100001110011100001101010001101010011011110101100100110110011001111110111100100000011101000000100010011101110111100111100111100011001000111010110100101100110111101010010111110000100100001110101011000010101110010010100101110001001101010101001100000111010011110001000010100000100010000010000110011100111100110011100110111101011101001000110110011001011010101100110111111110001011110000100100011110111100011111011111011100110011011100010111010110010111101010001100010001010010111111101110011010101000010000011100000110001100110100001010011010111000000110001010110000110000000100111000101010000010100000110111111111001100100101001111001010010101101101100111010000001100101100100101010111010000011101000100011011111010101100000011100100101110001100100010010010100010000100100100111101101110110111101011001111011011101001110110100101111110001010110010000101111011110111011100111100110000110000010101001101001101000111010100110011000101010001110100110101101110011111010110010010111110111101100111100101110110011110100100000101000101100111000100011001111110001000010010001010101110001110000111100110001101111110110001001001100101110001010111111000111000100011001110001010101000100110001000101110110101000000001100010001000101110000000010001001001100110100100011100101101010010100001011111001011010011001000101101101001111001100101011101111110111101101100111110000100110110011110000111111011010010010011011100100101000000111110110010101110010011000111101101011111110001100101100011111110111111100111001011001010010101000011001110binp = 0b10011001100000011101010111000011011000001101101000010101101110001111101010101100110000100111101101000100011101001011001100101000110010001000100001010011011100110011001110111001101010000111100000111110110101011101110000010111111101101111001011111111101100010011010001000011000100000010111111001000100000010001010001110101101011001100110001100000001100111010010011010101000011001101111011001110101111111011111101010100100000111101010101001101110000010101100011111001111100001100111010000111100110000001010001001101111111111100010010010001100110000011100110100100001000001001011010000000010100100011001000000000000010100111010011000111011010001010111010001000101100101011001001101101001101101001110101111011010110100101000000001111000001100101000000010101011011011100000001010001111000000100110011011001010011101000010101100101001000001100111001101000111101000000111001110010100001111100101001001101001101000011111001001000101001100101010001011010101111001001101110011101011001011110000001000100100110110001011010101000111001111001011001000001011111110000111000001100011110000011001110000010110101010000000101001111111011100010000000111001110100000010001101100110111010100000011101000100111011111011110001011001110000010001101010011110100110100111001000100010000110110110010111100101111010011110011110100000001001110111100111101000100011011100011101111100101100110110100011101110001111111110010001000001101111100100101011111110111110010100101010110111010111110010110111101011101111110110110101001111101101000010010100000101111000100010110100010011101000100111000011111100111010011010011101110110000100101100101010111111000110100010010101001000001111001100100110101000100110101001011110111101010101110001111101111001110000101000001010110011111000000010010100010000111011001000111000011000011110100000111101101011100000101000111011101110101100101001110001101000111100111011110000110010101010000100110100011010111110111100010111111101010110001000010010011110111101000110001100101111000111101010101101101100100010110011101111101000011101100000101001111001binc = 0b1111010111110100110011100100001100111101111000010010000010010011101110101000101000100011111101011100110010010111111010000111001101010101010111100000000100111111001111110001111011110100001111001001010001000000011110000001001000011010100111100011110011011010011010011011111111100100110000110010011101110111001001011010101001101011100110101110001111111100100111011010011001001001100010110100000011100000000100110010101100000001010000101000100010000101101111010101000001000110011101100101010111110111000100001011110101010011010010110111010010100101001001010011000100110010010010110100101001111001111000011011000000110000111111001101001111010011110101001001111111110001001100011100101100011110110101000110010110110110101110110110111010110111100101101000111101101011000010011001111111010111000001100101001010010110111100100100100011110101010010010010010100100011001100011111010011101101101101000010101101011000100101101100001000000001101111111100100101111000101011001010010011000011001101101110101001011111010110000111111111011000101100000000011001010000000111110000001101101100101010010001101101010101000010010010110101110100100110011001001011101011111110011100000100001100010100000101011100001110101101011011110000101110011011100010100101010011101011001011011111100001100010000010110010001111010000110010000011100010010101110000101011110000111101001110001111111111101011000110001111011100100111000010110001111110100100011110000100010000011101110101111101000110100110111101110001011101110100001101101100011111000010101111100011100011011001011110010000000001010010101100111001111110110101000010110101110001011000101101110100110111100000110101101010010111001101000010001101110011101010111111011001110000001110000110001000101110110010001001001101010011110100000010100000100010110000001000011001011010000010111010100100101010100010011001100111011110111100101111100000100110110110101101110100011011101101100000101111000011110011000010000000100010000011110110010000010101001110000111110111110001001101000010011101010101101111101010100001101010111010000010000h = binz
c = binc
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);# Solve SVP. f*h = g (mod p) 求f,g
f,g = m.LLL()[0]
mf = f*c % p % g
m = mf * inverse_mod(f, g) % g
long_to_bytes(m)
#NSSCTF{c6ff8aba-fda9-497a-91a7-ee1ac5da68ab}
相关文章:
[NSSRound#11] 密码学个人赛
这个比赛没有参加,跟别人要了些数据跑一下,其实交互这东西基本上一样,跑通就行. ez_enc 这题有点骗人,给了一堆AB串,一开始以为是培根密码,结果出来很乱.再看长度:192 应该就是01替换 a ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAA…...

玩转树莓派四、修改国内源提高更新速度
树莓派的软件包源默认连接的是官方源,速度不是很快,我们可以更换为第三方源以提高下载速度和体验。 首先通过命令 lsb_release -a 获取到版本号为 bullseye piRpi4B2G:/etc/apt $ lsb_release -a No LSB modules are available. Distributor ID: Debian Descripti…...
苹果手机网速慢怎么办?这些方法帮你解决网速慢的问题!
案例:苹果手机数据网络信号差,怎么解决? 【家人们,苹果手机不知咋回事,网速很慢,想要在某宝买个东西都得卡个半天。哭了!有没有什么方法解决?】 苹果手机作为一款高端智能手机&…...
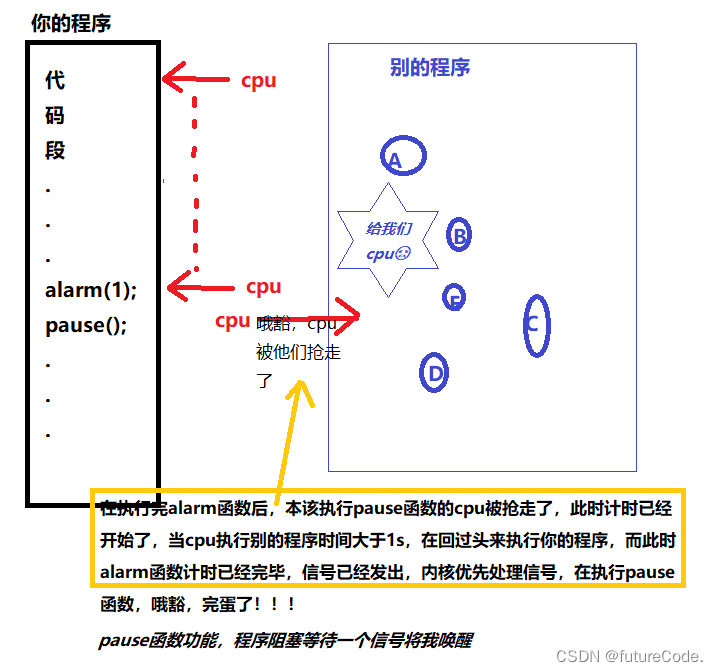
linux_时序竞态-pause函数-sigsuspend函数-异步I/O-可重入函数-不可重入函数
接上一篇:linux_信号捕捉-signal函数-sigaction函数-sigaction结构体 今天来分享时序竞态的知识,关于时序竞态的问题,肯定会和cpu有关,也会学习两个函数,pause函数,sigsuspend函数, 也会分享什么…...

Tomcat的负载均衡和动静分离
---------------------NginxTomcat负载均衡、动静分离------------------------- Nginx 服务器:192.168.80.10:80 Tomcat服务器1:192.168.80.100:80 Tomcat服务器2:192.168.80.101:8080 192.168.80.101:8081 1.部署Nginx 负载均衡器 system…...
C++每日一练:最长递增区间 阿波罗的魔力宝石 投篮
文章目录 前言一、最长递增区间二、阿波罗的魔力宝石三、投篮总结 前言 今天的题太简单,甚至 “最长递增区间” 和 “投篮” 就是一个问题。实在没事干,也给做了!直接上代码算了… 提示:以下是本篇文章正文内容 一、最长递增区间…...
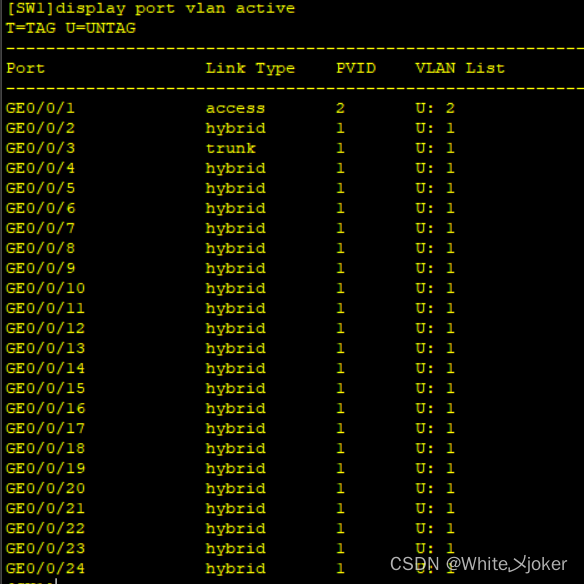
HCIP之VLAN
目录 网络的三层架构 接入层 无线的缺陷: 上网用户数量增多,网络卡顿的原因 CSMA/CD --- 载波侦听多路访问/冲突检测 CSMA/CA --- 载波侦听多路访问/冲突避免 无线网络没有使用冲突检测技术的原因 汇聚层 连接两条线路的原因 核心层 VLAN VLAN配…...
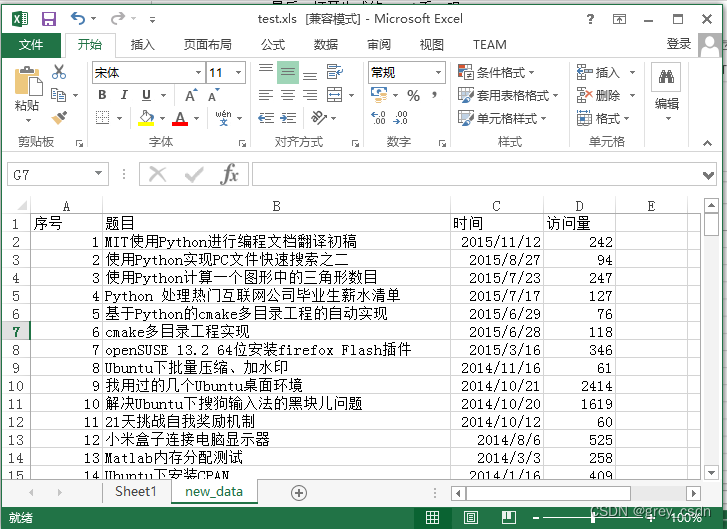
1686_MATLAB处理Excel文件
全部学习汇总: GreyZhang/g_matlab: MATLAB once used to be my daily tool. After many years when I go back and read my old learning notes I felt maybe I still need it in the future. So, start this repo to keep some of my old learning notes servral …...

亿发软件:中大型仓库进出货管理系统解决方案,定制软件让仓储作业高效便捷
中大型仓库出入库管理是传统厂家供应链管理流程的重要部分,直接关乎货物在仓库当中存储的安全,和员工工作的效率。一旦仓库管理当中出现了疏漏,那么货物的信息数据就会发生变动,导致实际与账目不符。人工带来的低效与不可控是传统…...
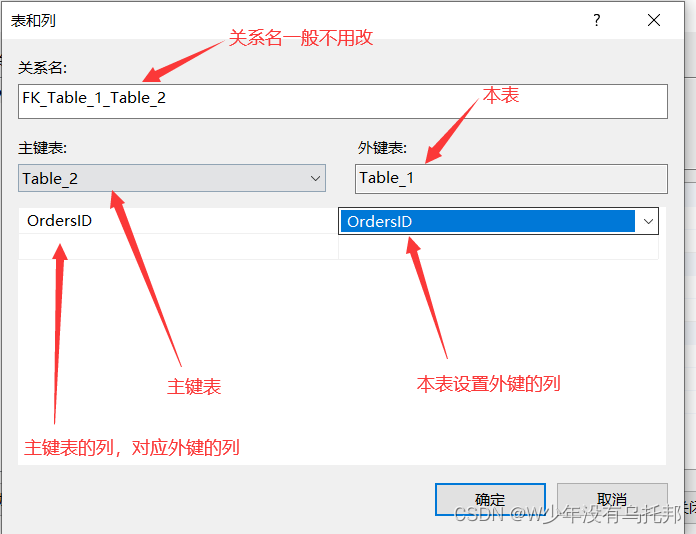
SQL Server基础 第二章 表结构管理
目录 一、数据类型 1,字符类数据类型 2,数值型数据类型 3,日期/时间型数据类型 二、主键(Primary key) 三、默认值 四、唯一键(Unique) 五、自增标识 六、约束 七、外键 一、数据类型 …...

华为OD机试真题(Java),最小步骤数(100%通过+复盘思路)
一、题目描述 一个正整数数组 设为nums,最大为100个成员,求从第一个成员开始正好走到数组最后一个成员所使用的最小步骤数。 要求: 第一步 必须从第一元素起 且 1<第一步步长<len/2 (len为数组长度);从第二步开始只能以所…...

3分钟搞懂:JavaScript 和 ECMAScript
JavaScript 和 ECMAScript ECMAScript 是 JavaScript 语言的国际标准,JavaScript 是 ECMAScript 的一种实现(Adobe ActionScript 和 JScript 同样实现了 ECMAScript)。 ECMAScript 是欧洲计算机制造商协会 ECMA(European Comput…...

Bito:一款 iead/webstorm 神级插件,由 ChatGPT 团队开发,堪称辅助神器
前言: idea(后端),webstorm(前端)中可以用的一款辅助插件:Bito 个人尝试体验效果: 优点是:可以自动完成一些场景代码。 缺点:太慢了,大部分时间一直转圈 摘取文档: 什么是Bito&…...

[ 云原生 | Docker ] 构建高可用性的 SQL Server:Docker 容器下的主从同步实现指南
文章目录 一、前言二、SQL Server 主从同步的原理介绍三、具体的搭建过程3.1 准备工作3.1.1 卸载旧版本(如果有,可选,非必须)3.1.2 安装 Docker3.1.3 验证本地 Docker 是否安装成功 3.2 创建 Docker 网络3.3 创建主从节点的 SQL S…...

Binary Utilities非默认目录构建和安装
在AppArmor零知识学习六、源码构建(3)中,详细介绍了libapparmor的构建步骤,但那完全使用的是官网给出的默认参数。如果需要将目标文件生成到指定目录而非默认的/usr,则需要进行一些修改,本文就来详述如何进…...

【故障检测】基于 KPCA 的故障检测【T2 和 Q 统计指数的可视化】(Matlab代码实现)
💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥 🏆 博主优势: 🌞 🌞 🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 …...

从“捐赠openEuler”到“向openEuler捐赠”,openEuler生态走入高速发展期
【中国,上海,2023年4月21日】openEuler Developer Day 2023于4月20-21日在线上和线下同步举办。本次大会由开放原子开源基金会指导,中国软件行业协会、openEuler社区、边缘计算产业联盟共同主办,以“万涓汇流,奔涌向前…...
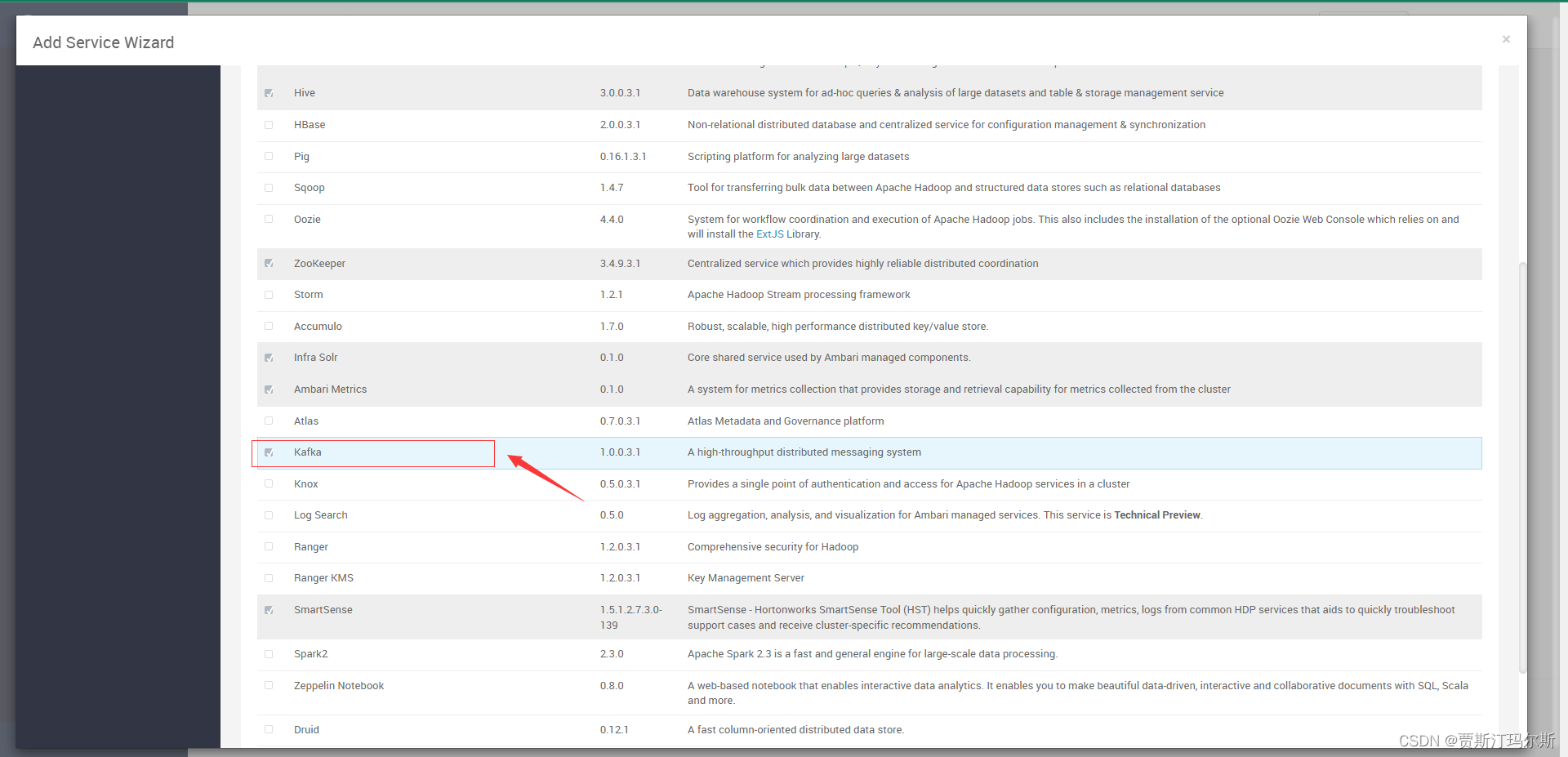
ambari的kafka服务开启sasl
添加 sasl 配置⽂件 集群部署 Kafka2.2下载地址 http://archive.apache.org/dist/kafka/2.2.1/kafka_2.11-2.2.1.tgz 解压安装包 tar -zxvf kafka_2.11-2.2.1.tgz 部署略 ambari 数据kafka服务 在kafka的conf目录下创建sasl_conf目录,将kafka_client_jaas.conf/kafka_se…...
改善内部客户服务的 3 个技巧
在当今世界,许多公司都专注于改善客户关系管理,公司管理层面临的挑战是他们不仅拥有外部客户,员工也是有痛点和需求的内部客户。正如糟糕的客户服务会导致客户流失一样,糟糕的内部客户服务会增加员工流动率。在当今瞬息万变的就业…...

使用Apache POI的SXSSFworkbook实现大量数据导出到Excel文件
Apache POI是一个开源的、用来读写微软Excel文件的Java工具包,一般用来读取Excel文件中的数据或者将数据导出到Excel文件。HSSFWorkbook用来处理早期版本的Excel文件(xls格式),而XSSFWorkbook用来处理新版本Excel文(xl…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
