代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离
代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离
- 583. 两个字符串的删除操作
- 72. 编辑距离
583. 两个字符串的删除操作
题目链接:583. 两个字符串的删除操作,难度:中等
【实现代码】
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) {dp[i][0] = i;}for (int j = 0; j <= word2.size(); j++) {dp[0][j] = j;}for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp.back().back();}
};
【解题思路】
动规五部曲
- 确定dp数组(dp table)以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
- 确定递推公式:当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
a) 情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1;
b) 情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1;
c) 情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);- dp数组如何初始化:dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。dp[0][j]的话同理
- 确定遍历顺序:遍历的时候一定是从上到下,从左到右
- 举例推导dp数组
72. 编辑距离
题目链接:72. 编辑距离,难度:困难
【实现代码】
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) {dp[i][0] = i;}for (int j = 0; j <= word2.size(); j++) {dp[0][j] = j;}for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}) + 1;}}}return dp.back().back();}
};
【解题思路】
动规五部曲
- 确定dp数组(dp table)以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
- 确定递推公式:当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
a)word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作,即 dp[i][j] = dp[i - 1][j] + 1
b) 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。即 dp[i][j] = dp[i][j - 1] + 1;
word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word1删除元素’d’ 和 word2添加一个元素’d’,变成word1=“a”, word2=“ad”, 最终的操作数是一样
c) 只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。所以 dp[i][j] = dp[i - 1][j - 1] + 1;- dp数组如何初始化:dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。dp[0][j]的话同理
- 确定遍历顺序:遍历的时候一定是从上到下,从左到右
- 举例推导dp数组
相关文章:

代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离
代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离 583. 两个字符串的删除操作72. 编辑距离 583. 两个字符串的删除操作 题目链接:583. 两个字符串的删除操作,难度:中等 【实现代码】 class Solution { publi…...
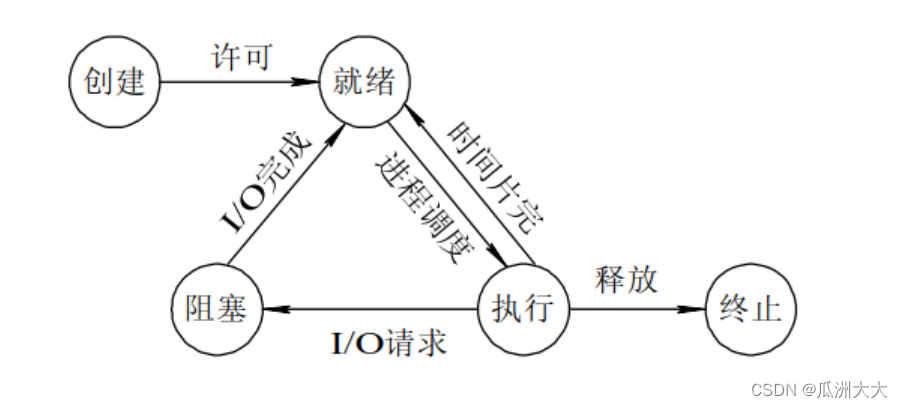
【嵌入式笔/面试】嵌入式软件基础题和真题总结——操作系统
在学习的时候找到几个十分好的工程和个人博客,先码一下,内容都摘自其中,有些重难点做了补充! 才鲸 / 嵌入式软件笔试题汇总 嵌入式与Linux那些事 阿秀的学习笔记 小林coding 百问网linux 嵌入式软件面试合集 2022年春招实习十四面…...
)
2023浙江省赛“信息安全管理与评估“--Web渗透测试(高职组)
2022全国职业技能大赛“信息安全管理与评估”(高职组)任务书 2022全国职业技能大赛“信息安全管理与评估”任务书第一阶段竞赛项目试题第二阶段竞赛项目试题第三阶段竞赛项目试题任务2:Web渗透测试2022全国职业技能大赛“信息安全管理与评估”任务书 第一阶段竞赛项目试题 …...

垃圾收集器面试总结(二)
G1 收集器 G1 (Garbage-First) 是一款面向服务器的垃圾收集器,主要针对配备多颗处理器及大容量内存的机器。 以极高概率满足 GC 停顿时间要求的同时,还具备高吞吐量性能特征。 被视为 JDK1.7 中 HotSpot 虚拟机的一个重要进化特征。它具备以下特点: 并行与并发&am…...

语音交友app开发中的用户积分系统
引言 在当今数字时代,语音交友app已成为一种流行的社交工具。它们给用户提供了一个平台,在这里他们可以结交新朋友,分享他们的生活和信仰,并建立深厚的人际关系。然而,市场上存在大量的语音交友app,这使得…...

Nature:惊人的突破!科学家们成功破译人类嗅觉感应机制的奥秘!
加州大学旧金山分校(UCSF)的科学家们创造了第一张关于气味分子如何激活人类气味受体的分子水平的3D图片,这是破译嗅觉的关键一步,该成果打破了长期以来研究人员对嗅觉理解的僵局。 该研究成果于2023年3月15日发表在《Nature》&…...
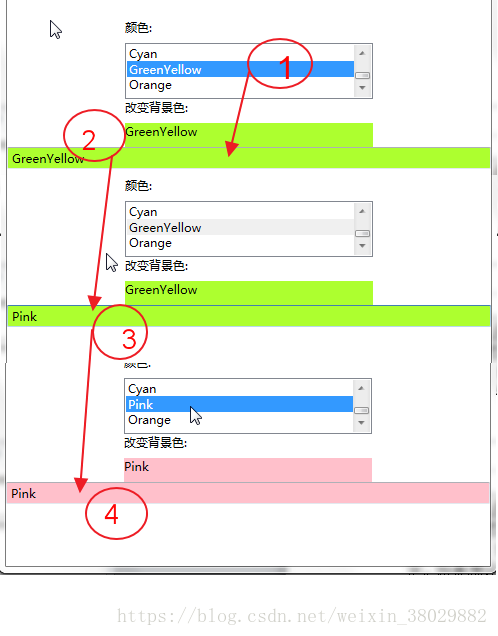
WPF教程(九)--数据绑定(2)--绑定模式
一、绑定模式 绑定模式以及模式的使用效果。 示例如下是根据ListBox中的选中项,去改变TextBlock的背景色。将 TextBlock 的背景色绑定到在 ListBox 中选择的颜色。在下面的代码中针对TextBlock的 Background 属性使用绑定语法绑定从 ListBox 中选择的值。代码如下。…...
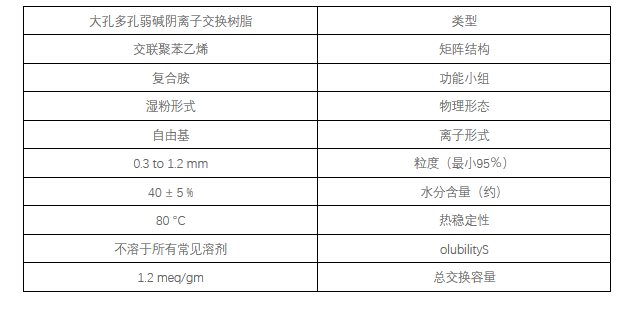
湿法冶金以及铼提取工艺,湿法冶金工艺特点及工艺流程
湿法冶金是利用浸出剂在一定温度压力下与矿石接触,把矿石中有用的金属溶解后再从溶液中回收有价金属的一种工艺,因为其过程大都是在水溶液中进行,所以又被称为“水法冶金”。 01 湿法冶金工艺特点及工艺流程 湿法冶金作为解决我国金属矿产资…...

kafka集群搭建
1.本次搭建涉及3台centos7主机,防火墙与selinux服务均关闭 2.主机参数如下表所示 nameIPportserviceA10.1.60.1122128、2888、3888、9092kafka、zookeeperB10.1.60.1142128、2888、3888、9092kafka、zookeeperC10.1.60.1152128、2888、3888、9092kafka、zookeeper…...
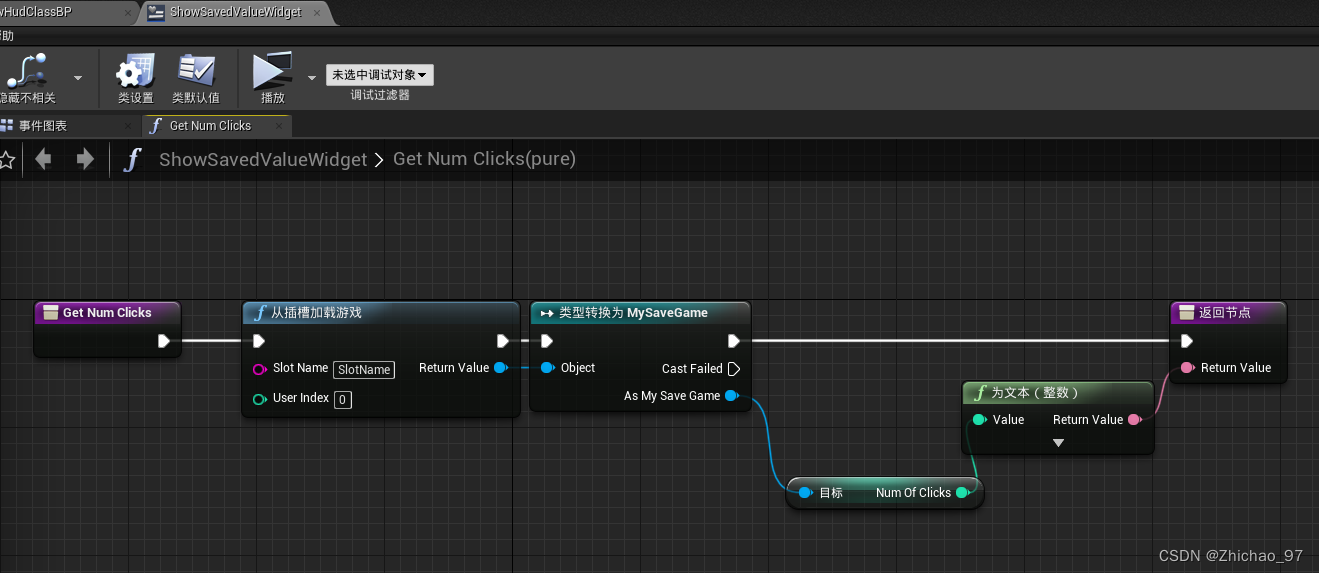
【UE】将存档的值显示在控件蓝图上
上一篇博客(【UE】保存游戏的demo)已经实现了存档功能,本篇博客介绍的是如何将存档的值显示在控件蓝图上。 效果 可以看到我们存档的值显示在文本控件上 步骤 1. 新建一个蓝图类,父类为“HUD” 命名为“NewHudClassBP” 2. 在世…...

考研数据结构代码篇
文章目录 数据结构线性表基本操作顺序表的定义顺序表基本操作 单纯上传一下数据结构中可能考察的代码,规格很乱,过几天改规格,提前水一篇 数据结构 线性表 基本操作 InitList(&L) // 初始化表。构造一个空的线性表L࿰…...

css-设置单行文本溢出省略号,使用overflow:hidden属性之后的出现的问题几解决办法。
1 设置单行文本溢出后出现省略号 必要:需要设置固定宽度,不允许换行 width: 200px; white-space: nowrap; overflow: hidden; text-overflow: ellipsis; display: -webkit-box; -webkit-line-clamp: 1; -webkit-box-orient: vertical; 2 设置N行文本…...

js的方法
字符串方法: substring(startIndex, endIndex):从指定的字符串中提取字符并返回新字符串,不包括结束位置的字符。substr(startIndex, length):从指定字符串中提取指定长度的字符并返回新字符串。indexOf(searchValue, startIndex…...
[NSSRound#11] 密码学个人赛
这个比赛没有参加,跟别人要了些数据跑一下,其实交互这东西基本上一样,跑通就行. ez_enc 这题有点骗人,给了一堆AB串,一开始以为是培根密码,结果出来很乱.再看长度:192 应该就是01替换 a ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAA…...

玩转树莓派四、修改国内源提高更新速度
树莓派的软件包源默认连接的是官方源,速度不是很快,我们可以更换为第三方源以提高下载速度和体验。 首先通过命令 lsb_release -a 获取到版本号为 bullseye piRpi4B2G:/etc/apt $ lsb_release -a No LSB modules are available. Distributor ID: Debian Descripti…...
苹果手机网速慢怎么办?这些方法帮你解决网速慢的问题!
案例:苹果手机数据网络信号差,怎么解决? 【家人们,苹果手机不知咋回事,网速很慢,想要在某宝买个东西都得卡个半天。哭了!有没有什么方法解决?】 苹果手机作为一款高端智能手机&…...
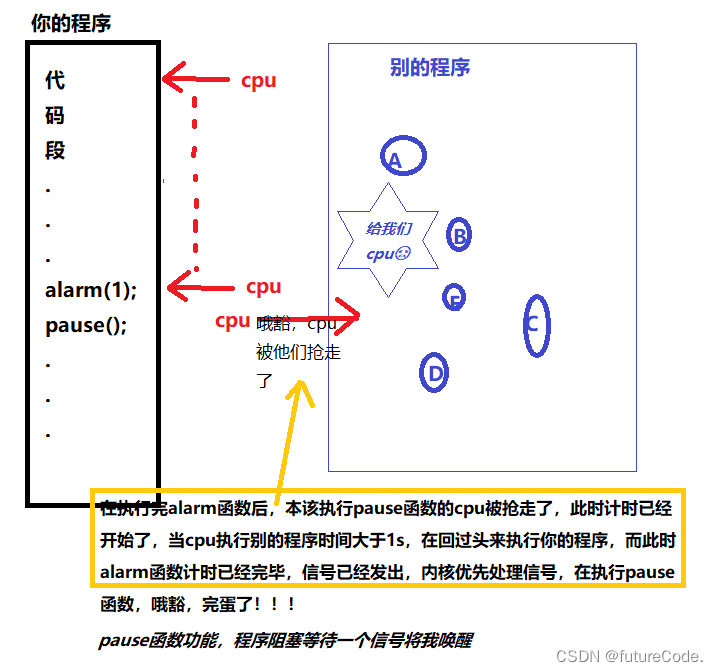
linux_时序竞态-pause函数-sigsuspend函数-异步I/O-可重入函数-不可重入函数
接上一篇:linux_信号捕捉-signal函数-sigaction函数-sigaction结构体 今天来分享时序竞态的知识,关于时序竞态的问题,肯定会和cpu有关,也会学习两个函数,pause函数,sigsuspend函数, 也会分享什么…...

Tomcat的负载均衡和动静分离
---------------------NginxTomcat负载均衡、动静分离------------------------- Nginx 服务器:192.168.80.10:80 Tomcat服务器1:192.168.80.100:80 Tomcat服务器2:192.168.80.101:8080 192.168.80.101:8081 1.部署Nginx 负载均衡器 system…...
C++每日一练:最长递增区间 阿波罗的魔力宝石 投篮
文章目录 前言一、最长递增区间二、阿波罗的魔力宝石三、投篮总结 前言 今天的题太简单,甚至 “最长递增区间” 和 “投篮” 就是一个问题。实在没事干,也给做了!直接上代码算了… 提示:以下是本篇文章正文内容 一、最长递增区间…...
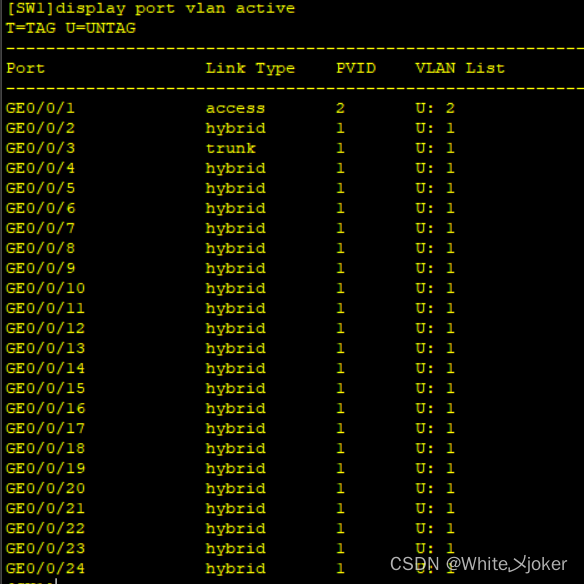
HCIP之VLAN
目录 网络的三层架构 接入层 无线的缺陷: 上网用户数量增多,网络卡顿的原因 CSMA/CD --- 载波侦听多路访问/冲突检测 CSMA/CA --- 载波侦听多路访问/冲突避免 无线网络没有使用冲突检测技术的原因 汇聚层 连接两条线路的原因 核心层 VLAN VLAN配…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
