leetcode (重排数组使得)连续子数组的权值和最小
- 题目描述:请重新排列某个仅包含2和3的数组,使得数组的所有连续子数组权值之和最小
- 数组的权值定义为,数组中所有元素之积的因子个数,例如:rank([2,3])=4
x = p 1 c 1 × p 2 c 2 × p 3 c 3 ⋅ ⋅ ⋅ × p k c k r a n k = ( c 1 + 1 ) × ( c 2 + 1 ) × ( c 3 + 1 ) ⋅ ⋅ ⋅ × ( c 2 + 1 ) x = p_1^{c_1} \times p_2^{c_2}\times p_3^{c_3} \cdot\cdot\cdot \times p_k^{c_k}\\ rank = (c_1+1)\times (c_2+1) \times (c_3+1) \cdot\cdot\cdot \times (c_2+1) x=p1c1×p2c2×p3c3⋅⋅⋅×pkckrank=(c1+1)×(c2+1)×(c3+1)⋅⋅⋅×(c2+1)
- 本题 P1=2 ,P2 =3,2和3互质,所以子数组的权值为(2的个数+1)*(3的个数+1)
2 n + 1 个数字, n + 1 个 2 , n 个 3 ,长度为 2 n 的连续子数组的权值 顺序的情况 : ( n + 1 + 1 ) ∗ ( n − 1 + 1 ) + ( n + 1 + 1 ) ∗ ( n − 1 + 1 ) = ( n + 2 ) ∗ ( n ) + ( n + 2 ) ∗ ( n ) 乱序为 : ( n + 1 ) ∗ ( n + 1 ) + ( n + 1 ) ∗ ( n + 1 ) 2n+1个数字,n+1个2,n个3,长度为2n的连续子数组的权值\\ 顺序的情况 : \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (n+1+1)*(n-1+1)+ (n+1+1)*(n-1+1)\\ = (n+2)*(n)+ (n+2)*(n)\\ 乱序为: \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (n+1)*(n+1)+(n+1)*(n+1) 2n+1个数字,n+1个2,n个3,长度为2n的连续子数组的权值顺序的情况: (n+1+1)∗(n−1+1)+(n+1+1)∗(n−1+1)=(n+2)∗(n)+(n+2)∗(n)乱序为: (n+1)∗(n+1)+(n+1)∗(n+1)
例如:[2,2,2,3,3]和[2,2,3,3,2]的长度为4的连续子数组
- 所以在和的个数相同的情况下,越分散乘积就越大,越集中乘积就越小,排列应为顺序的情况
对于某个权值为 K 的数组,将 2 换成 3 的权值为 K ∗ ( N 2 − 1 ) + 1 N 2 + 1 ∗ ( N 3 + 1 ) + 1 N 3 + 1 对于某个权值为K的数组,将2换成3的权值为\\ K*\frac{(N_2-1) +1}{ N_2+1}*\frac{(N_3+1)+1}{N_3+1} 对于某个权值为K的数组,将2换成3的权值为K∗N2+1(N2−1)+1∗N3+1(N3+1)+1
例如:[2,2,2],K=(3+1) * (0+1)=4,
[2,2,3]K= (2+1) * (1+1)=6 = 4* 3 4 \frac{3}{4} 43* 2 1 \frac{2}{1} 12
CG
- 参考: 权值不超过K的连续子数组的数量
- 本题的解答,右边界从0到n,对于每个右边界,左边界从0开始,如果窗口中的因子数量满足条件(大于或等于K),则收缩左边界直到不满足条件,这样可以得出有几个满足条件的连续子数组。
- 注:在每次重新计算时,作者并没有将j,即左窗口放回到0,因为有边界扩大,之前的j个窗口满足条件,再窗口中加入数值只能增加权值
- 注:作者使用了匿名函数来计算当前窗口的权值: lambda 表达式——匿名函数 auto i= [ ] () { };, 填入 & 时,代表通过引用传递捕捉父作用域的变量 https://blog.csdn.net/lievech/article/details/121393346
#include <stdio.h>
#include<unordered_map>
#include<iostream>
#include<vector>
#define ll long long
using namespace std;
int main() {int n, k;cout<<"N长度的vector有多少连续子数组的权值不小于K"<<endl;cin >> n >> k;vector<int> a(n);unordered_map<int, int> mp;ll cnt = 1, res = 0;//因子数量(cnt)auto addv = [&](int x, int t) {for (int i = 2; i * i <= x; i++) {while (x % i == 0) {cout<<i<<" "<<mp[i]<<endl;cnt /= (mp[i] + 1);cout<<"cnt"<<"<-->"<<cnt<<endl;mp[i] += t;cnt *= (mp[i] + 1);cout<<"cnt"<<"<-->"<<cnt<<endl;x /= i;}}if (x > 1) {cnt /= (mp[x] + 1);cout<<"cnt"<<"-->"<<cnt<<endl;mp[x] += t;cnt *= (mp[x] + 1);}};for (int i = 0, j = 0; i < n; i++) {cin >> a[i];addv(a[i], 1);while (j <= i && cnt >= k) {addv(a[j], -1);j++;}res += j;}cout<<"----->";cout << res << "\n";
}N长度的vector有多少连续子数组的权值不小于K
3
4
6
2 0
cnt<-->1
cnt<-->2
cnt-->2
2 1
cnt<-->2
cnt<-->2
cnt-->1
N长度的vector有多少连续子数组的权值不小于K
3
4
9
3 0
cnt<-->1
cnt<-->2
3 1
cnt<-->1
cnt<-->3
6
2 0
cnt<-->3
cnt<-->6
cnt-->2
3 3
cnt<-->2
cnt<-->6
3 2
cnt<-->2
cnt<-->4
2 1
cnt<-->2
cnt<-->2
cnt-->1
2
cnt-->1
----->4
相关文章:
连续子数组的权值和最小)
leetcode (重排数组使得)连续子数组的权值和最小
题目描述:请重新排列某个仅包含2和3的数组,使得数组的所有连续子数组权值之和最小数组的权值定义为,数组中所有元素之积的因子个数,例如:rank([2,3])4 x p 1 c 1 p 2 c 2 p 3 c 3 ⋅ ⋅ ⋅ p k c k r a n k ( c 1 1 ) ( c …...
)
JSP计算机等级考试查询系统(源代码+论文+答辩PPT)
第一章 引言 计算机等级考试查询系统是有其开发的必要性的,它的应用将大大节省了学校的人力资源,从而从人工劳动中解脱出来。我们这次开发的软件系统一共包括了三个部分:等级考试的报名系统、查询系统和管理系统。其中管理系统是另外两部分…...

python 基础系列篇:七、以函数方式编写一个数字华容道
python 基础系列篇:七、以函数方式编写一个数字华容道 数字华容道游戏分析开始编写完整代码代码解说定义方法的规律 小结 数字华容道 嗯,就是一个简单的益智游戏,把数字按照特定规律排列,并比矩阵少一个格,用来进行移…...

2023年前端面试题
1.position都有哪些属性 2.1px等于多少rem,rem根据根元素的大小,根元素是谁 3.Es6操作数组的方法 4.防抖和节流以及应用场景 5.Vue和ajax最大的区别是什么(Vue和ajax怎么操作dom的,vue虚拟dom) 6.js数据类型有哪些&…...

快速入门量化交易
本文首发自「慕课网」,想了解更多IT干货内容,程序员圈内热闻,欢迎关注"慕课网"! 原作者:袁霄|慕课网讲师 近来“量化交易”这个词听得越来越频繁,多数人对量化交易的第一印象是“高大上的技术”…...

Mongodb oplog
在MongoDB复制集中,oplog信息存储在oplog.rs集合中。 oplog.rs集合是一个固定大小的集合(capped collection),它位于local数据库中。 当我们在源MongoDB实例上启用了复制(replication)功能,MongoDB会自动在local数据库中创建oplog.rs集合。此后,所有在该实例上的写操作都会生…...

python基础篇: python字符串方法都有哪些?你知道多少?
❝ Python提供了丰富的字符串处理方法,可以方便地对字符串进行操作、处理和转换。在本文中,我们将介绍Python中常用的字符串方法。 ❞ python中字符串内置方法很多,可以通过dir()方式查看具体有哪些方法,下表是python字符串的全部…...
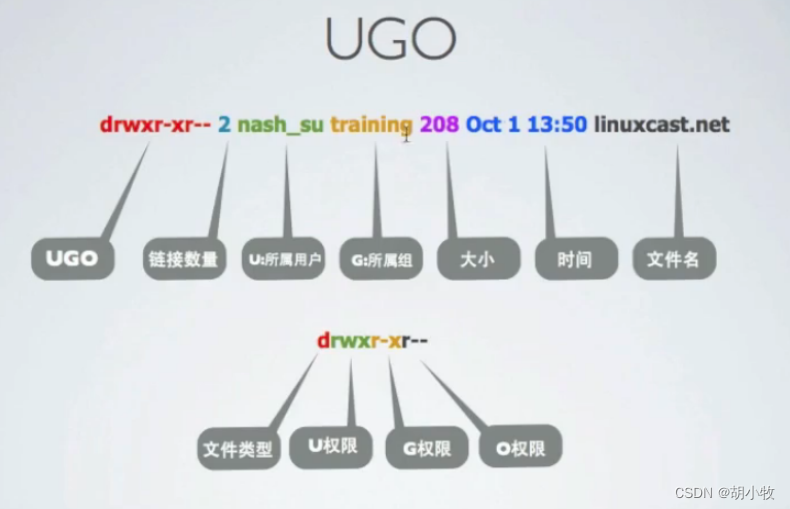
chmod 命令 (chmod 0660)
chmod的作用: 用于设置文件所有者和文件关联组的命令,就是控制用户的权限命令 注意事项: chown 需要超级用户 root 的权限才能执行此命令。 自己常用chmod 命令是 chmod 777 * 给所有文件权限 chmod 777 文件名 给单独文件权限 这个777 是怎么来的, 或者chmod 0660 这…...

Qt应用开发常用功能
Qt判断当前操作系统? #ifdef Q_OS_MAC //mac ... #endif#ifdef Q_OS_LINUX //linux ... #endif#ifdef Q_OS_WIN32 //win ... #endif#ifdef __arm__ //arm ... #endifQt实现应用程序关闭和重启? //关机按钮-点击槽函数 void SystemD::on_shutdownButton…...

麻了,部门新来的00后给我卷崩溃了...
今天上班开早会就是新人见面仪式,听说来了个很厉害的大佬,年纪还不大,是上家公司离职过来的,薪资已经达到中高等水平,很多人都好奇不已,能拿到这个薪资应该人不简单,果然,自我介绍的…...

代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离
代码随想录算法训练营第56天|583. 两个字符串的删除操作,72. 编辑距离 583. 两个字符串的删除操作72. 编辑距离 583. 两个字符串的删除操作 题目链接:583. 两个字符串的删除操作,难度:中等 【实现代码】 class Solution { publi…...
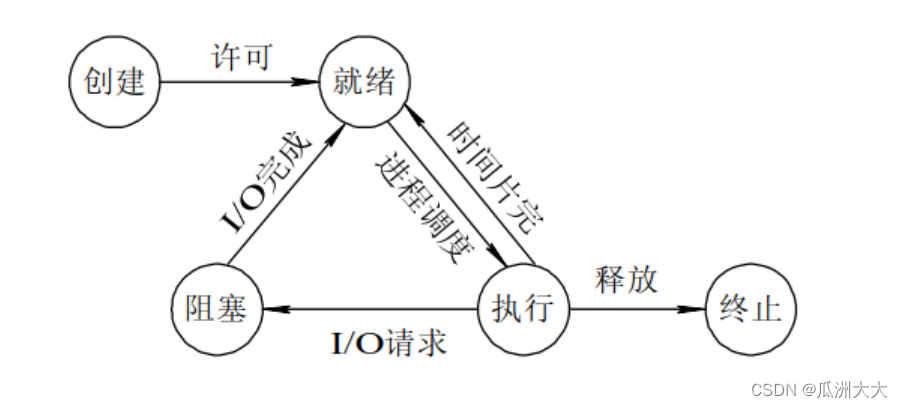
【嵌入式笔/面试】嵌入式软件基础题和真题总结——操作系统
在学习的时候找到几个十分好的工程和个人博客,先码一下,内容都摘自其中,有些重难点做了补充! 才鲸 / 嵌入式软件笔试题汇总 嵌入式与Linux那些事 阿秀的学习笔记 小林coding 百问网linux 嵌入式软件面试合集 2022年春招实习十四面…...
)
2023浙江省赛“信息安全管理与评估“--Web渗透测试(高职组)
2022全国职业技能大赛“信息安全管理与评估”(高职组)任务书 2022全国职业技能大赛“信息安全管理与评估”任务书第一阶段竞赛项目试题第二阶段竞赛项目试题第三阶段竞赛项目试题任务2:Web渗透测试2022全国职业技能大赛“信息安全管理与评估”任务书 第一阶段竞赛项目试题 …...

垃圾收集器面试总结(二)
G1 收集器 G1 (Garbage-First) 是一款面向服务器的垃圾收集器,主要针对配备多颗处理器及大容量内存的机器。 以极高概率满足 GC 停顿时间要求的同时,还具备高吞吐量性能特征。 被视为 JDK1.7 中 HotSpot 虚拟机的一个重要进化特征。它具备以下特点: 并行与并发&am…...

语音交友app开发中的用户积分系统
引言 在当今数字时代,语音交友app已成为一种流行的社交工具。它们给用户提供了一个平台,在这里他们可以结交新朋友,分享他们的生活和信仰,并建立深厚的人际关系。然而,市场上存在大量的语音交友app,这使得…...

Nature:惊人的突破!科学家们成功破译人类嗅觉感应机制的奥秘!
加州大学旧金山分校(UCSF)的科学家们创造了第一张关于气味分子如何激活人类气味受体的分子水平的3D图片,这是破译嗅觉的关键一步,该成果打破了长期以来研究人员对嗅觉理解的僵局。 该研究成果于2023年3月15日发表在《Nature》&…...
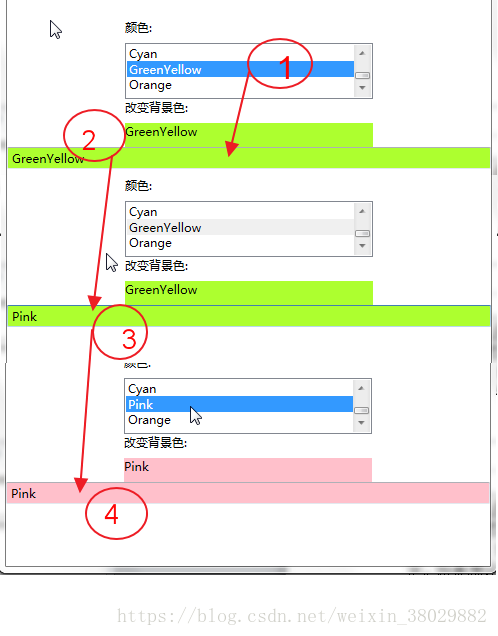
WPF教程(九)--数据绑定(2)--绑定模式
一、绑定模式 绑定模式以及模式的使用效果。 示例如下是根据ListBox中的选中项,去改变TextBlock的背景色。将 TextBlock 的背景色绑定到在 ListBox 中选择的颜色。在下面的代码中针对TextBlock的 Background 属性使用绑定语法绑定从 ListBox 中选择的值。代码如下。…...
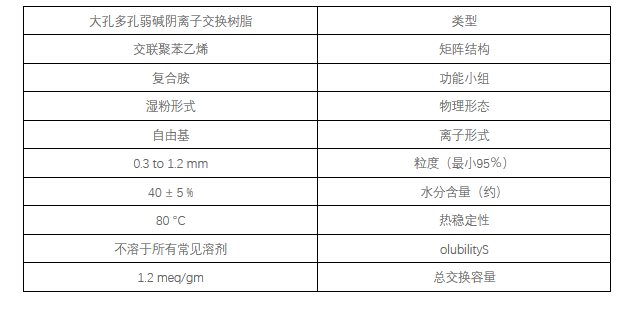
湿法冶金以及铼提取工艺,湿法冶金工艺特点及工艺流程
湿法冶金是利用浸出剂在一定温度压力下与矿石接触,把矿石中有用的金属溶解后再从溶液中回收有价金属的一种工艺,因为其过程大都是在水溶液中进行,所以又被称为“水法冶金”。 01 湿法冶金工艺特点及工艺流程 湿法冶金作为解决我国金属矿产资…...

kafka集群搭建
1.本次搭建涉及3台centos7主机,防火墙与selinux服务均关闭 2.主机参数如下表所示 nameIPportserviceA10.1.60.1122128、2888、3888、9092kafka、zookeeperB10.1.60.1142128、2888、3888、9092kafka、zookeeperC10.1.60.1152128、2888、3888、9092kafka、zookeeper…...
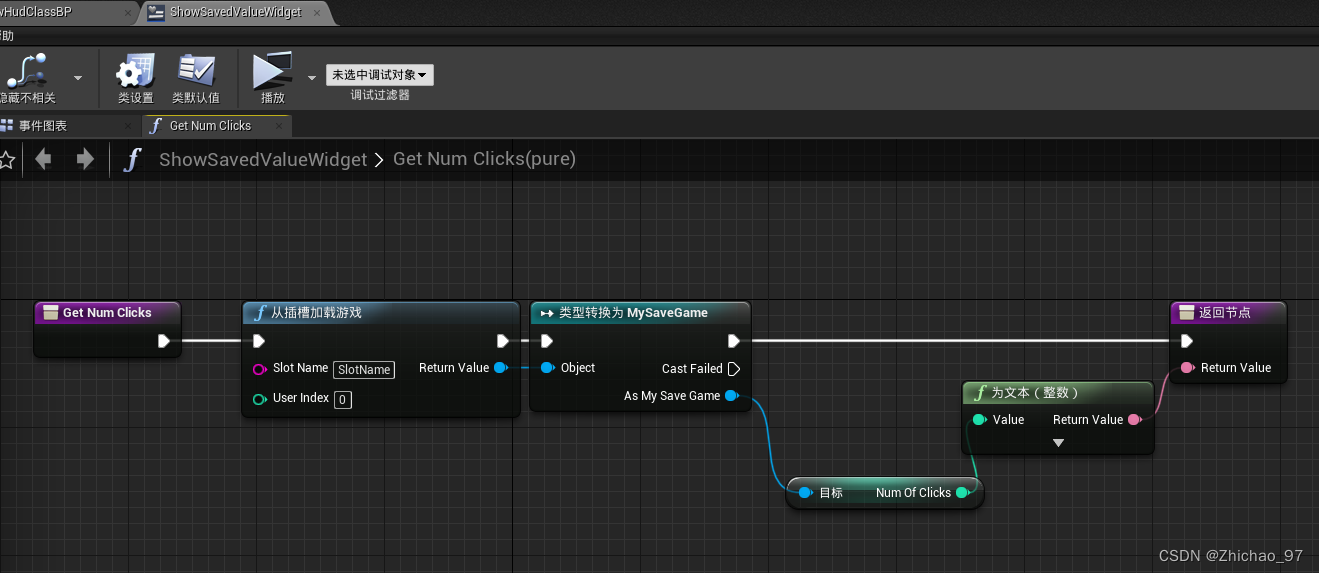
【UE】将存档的值显示在控件蓝图上
上一篇博客(【UE】保存游戏的demo)已经实现了存档功能,本篇博客介绍的是如何将存档的值显示在控件蓝图上。 效果 可以看到我们存档的值显示在文本控件上 步骤 1. 新建一个蓝图类,父类为“HUD” 命名为“NewHudClassBP” 2. 在世…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
