Python数据结构与算法-欧几里算法(p95)
一、欧几里算法原理
欧几里得公式
欧几里得算法:gcd(a,b) = gcd(b, a mod b) ; mod是指模,即a/b取余数。
运算示例: gcd(60,21)= gcd(21,18) = gcd(18,3)=gcd(3,0)
证明略
最大公约数-欧几里得求解
(1)最大公约数定理
约数:如果整数a能被整数b整除,那么a叫做b的倍数,b叫做a的约数。
给定两个整数a,b,两个数的所有公共约数中的最大值即为最大公约数 (Greatest Common Divisor, GCD)
例:12与16的最大公约数是4。
最大公约数求解:
欧几里得,又叫辗转相除法
《九章算术》:更相减损术
(2)最大公约数求解-欧几里得算法实现
def gcd_1(a,b): # 最大公约数-递归,a,b是两个数值if b == 0: # 递归终止条件return aelse:return gcd_1(b, a % b) # 公式gcd(a,b) = gcd(b, a mod b)print(gcd_1(12,16))def gcd_2(a, b): # 最大公约数-非递归,a,b是两个数值while b > 0: # b = 0时就得的a就是最后求的值r = a % b # 循环中a,b值一直在变化,需要先存储在一个变量中,不能直接用a%ba = bb = rreturn aprint(gcd_2(12,16))输出结果
4
4二、欧几里得算法应用——分数计算
1、提出问题
利用欧几里得算法实现一个分数类,支持分数的四则运算。
2、分数计算代码实现
(1)知识点—__add__()函数
__add__()方法是python的内置方法之一, 是一个一元函数。作用相当于求和运算。
1)__add__(self, other)是同一个类,两个对象相加的实现逻辑:
class Myclass(object):def __init__(self,value):self.value = valuedef __add__(self, other):return self.value + other.value
a = Myclass(1)
b = Myclass(2)
print(a + b) # 实现加法运算以上代码中,self 只本身对象,other 指另一个对象(同属于Myclass 类)
2)类外部加法使用
class Num:def __init__(self, x):self.x = xnumber = Num(5)
print(number.x.__add__(6))# 输出结果
113) __add__属性-拼接操作
可以进行拼接操作,拼接list和tuple。
b = [7, 8, 9, 10, 11, 12]
d = [19, 20, 21, 22, 23, 24]# 执行了拼接动作,拼接后的值被return出来
g = b.__add__(d)
print(g)# 输出结果
[7, 8, 9, 10, 11, 12, 19, 20, 21, 22, 23, 24](2)代码实现-加法
# 分数运算
class Fraction(): # 分数运算的类def __init__(self,a,b): # 传入参数属性,a,b是数字self.a = a # 分子self.b = b # 分母x = self.gcd(a, b) # 分子分母的最大公约数,x不是属性,不需要加self# 约分,分子和分母都除以最大公约数self.a = a / x # 分子化简self.b = b /x # 分母化简def gcd(self, a, b): # a,b最大公约数while b > 0:r = a % ba = b b = rreturn adef lcm(self, a, b): # 最小公倍数# 12 ,16 最大公约数为4# LCM = (12/4) * (16/4) * 4x = self.gcd(a, b)return a / x * b # (a / x) * (b / x) * x 的化简def __add__(self, other): # 加法,是内置函数# 1/12 + 1/20# 分母化成最小公倍数a = self.a # 分子b = self.b # 分母c = other.a # 分子d = other.b # 分母den = self.lcm(b, d) # 找到分母的最小功倍数,作为分母num_a = den / b * a # 换算分子anum_c = den / d * c # 换算分子cnum = num_a + num_c # 分子相加return Fraction(num, den) # 分子分母化简def __str__(self) -> str: # 类中的字符串显示的函数return "%d/%d" %(self.a, self.b) # %d表示十进制的整数f = Fraction(30,16) # 实例化类
print(f)a = Fraction(1, 12) # 1/12 实例化类
b = Fraction(1, 20) # 1/20 实例化类
print(a + b)输出结果
15/8
2/15相关文章:
)
Python数据结构与算法-欧几里算法(p95)
一、欧几里算法原理 欧几里得公式 欧几里得算法:gcd(a,b) gcd(b, a mod b) ; mod是指模,即a/b取余数。 运算示例: gcd(60,21) gcd(21,18) gcd(18,3)gcd(3,0) 证明略 最大公约数-欧几里得求解 (…...

【故障诊断】用于轴承故障诊断的性能增强时变形态滤波方法及用于轴承断层特征提取的增强数学形态算子研究(Matlab代码实现)
💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥 🏆 博主优势: 🌞 🌞 🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 …...

水羊转债,超达转债,晓鸣转债上市价格预测
水羊转债 基本信息 转债名称:水羊转债,评级:A,发行规模:6.94987亿元。 正股名称:水羊股份,今日收盘价:13.94元,转股价格:13.71元。 当前转股价值 转债面值 /…...
从数据管理到数据资产管理
数据已经与土地、劳动力、资本、技术并称为五种生产要素,数据的价值是毋庸置疑的。数据甚至成为了国家的基础性战略资源,数字经济也正在成为经济增长的强大创新动力。那么—— 数据到底指的是什么? 数据管理又是怎么回事? 数据如何…...

RabbitMQ【#1】是什么,有什么用
RabbiMQ是什么? RabbitMQ是一种开源的消息队列软件,它实现了高级消息队列协议(AMQP)并支持多种编程语言。它可以用于将消息从一个应用程序传递到另一个应用程序或进程,并支持分布式系统中的异步消息通信。RabbitMQ的主…...

RabbitMQ防止消息丢失
生产者没有成功把消息发送到MQ 丢失的原因 :因为网络传输的不稳定性,当生产者在向MQ发送消息的过程中,MQ没有成功接收到消息,但是生产者却以为MQ成功接收到了消息,不会再次重复发送该消息,从而导致消息的丢…...
)
ImageJ用户手册——第二部分(ImageJ操作)
ImageJ用户手册-第二部分 ImageJ的使用4. 使用键盘快捷键5. 查找命令6. 撤消和重做7. 图像类型和格式原生格式非原生格式 8. 堆栈、虚拟堆栈、超堆栈Stacks(堆栈)Virtual Stacks(虚拟堆栈)Hyperstacks(超堆栈ÿ…...

Java中Lambda表达式(面向初学者)
目录 一、Lambda表达式是什么?什么场景下使用Lambda? 1.Lambda 表达式是什么 2.函数式接口是什么 第二章、怎么用Lambda 1.必须有一个函数式接口 2.省略规则 3.Lambda经常用来和匿名内部类比较 第三章、具体使用场景举例() …...

2023年淮阴工学院五年一贯制专转本数字电子技术考试大纲
2023年淮阴工学院五年一贯制专转本数字电子技术考试大纲 一、考核对象 本课程的考核对象是五年一贯制高职专转本电子科学与技术专业普通在校生考生。 二、考试目的及总体要求 通过本课程的考试,检查学生对掌握数字电路的基础理论知识的掌握程度,是否…...

使用 GO 编写 Web 应用:学习如何使用 GO 语言编写 Web 应用,包括使用 HTTP 路由、模板引擎等。
GO 语言是一个高效、可靠和简洁的编程语言,越来越多的开发者开始选择 GO 语言来编写 Web 应用。本文将介绍如何使用 GO 语言编写 Web 应用,并且将重点关注使用 HTTP 路由和模板引擎。 使用 HTTP 路由 HTTP 路由是 Web 应用中非常重要的一个概念。它可以帮助我们将请求路由到…...
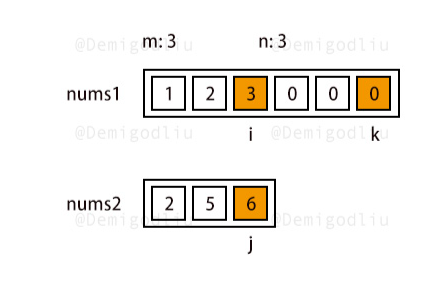
Leetcode-day4【88】【167】【125】【345】
文章目录 88. 合并两个有序数组题目解题思路解题思路【学习】尾插入法 167. 两数之和 II - 输入有序数组题目解题思路 125. 验证回文串题目解题思路 345. 反转字符串中的元音字母题目解题思路 88. 合并两个有序数组 题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums…...
【IoT】如何使用软件加密(文件夹加密工具.exe),并破解工具
目录 第一步:显示隐藏的文件。 第二步:将隐藏文件变成文件夹。 第三步:解密文件。 有时候出差或者有些商务场合,需要对一些敏感文件做一下简单的加密,这样在分享内容的时候,可以起到初步的保护作用。 当…...

Spring Boot——优雅的参数校验
🎈 概述 当我们想提供可靠的 API 接口,对参数的校验,以保证最终数据入库的正确性,是 必不可少 的活。比如下图就是 我们一个项目里 新增一个菜单校验 参数的函数,写了一大堆的 if else 进行校验,或者基础校…...
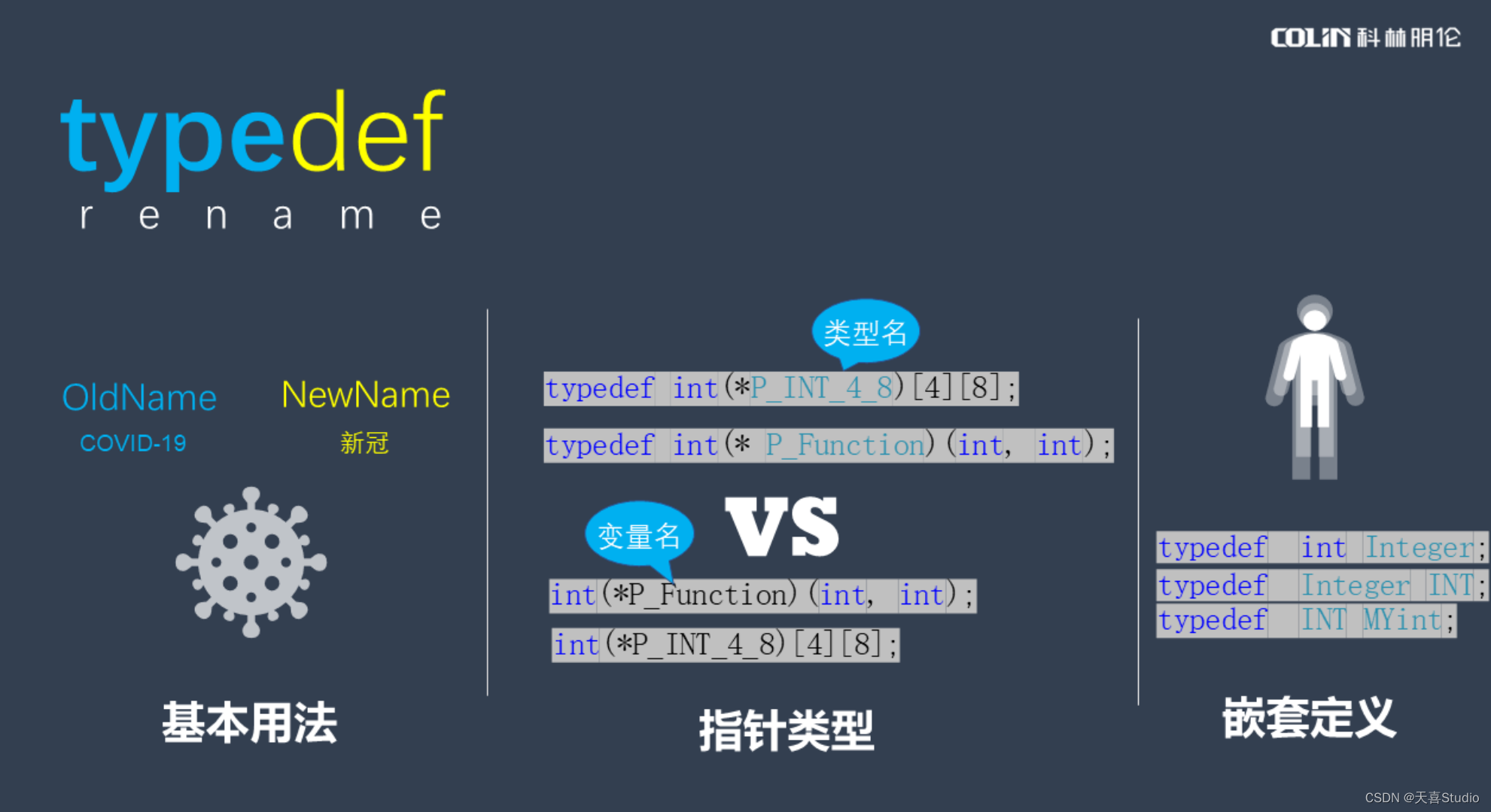
【c语言】typedef的基本用法 | 定义格式
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
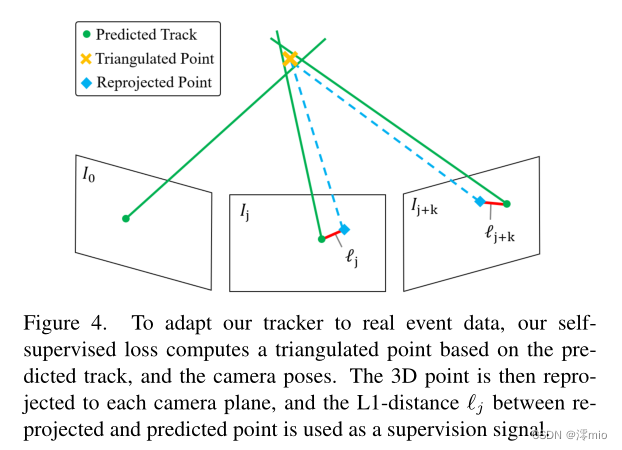
深度学习论文分享(二)Data-driven Feature Tracking for Event Cameras
深度学习论文分享(二)Data-driven Feature Tracking for Event Cameras(CVPR2023) 前言Abstract1. Introduction2. Related Work3. Method3.1. Feature Network3.2. Frame Attention Module3.3. Supervision 4. Experiments5. Con…...
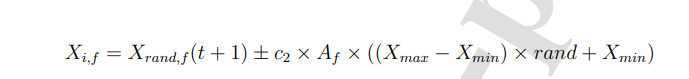
蛇优化算法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 蛇优化算法算法流程图初始化进化操作搜索阶段(无食物)——全局搜索搜索阶段(有食物)——局部搜索战斗模式交配模式 备…...
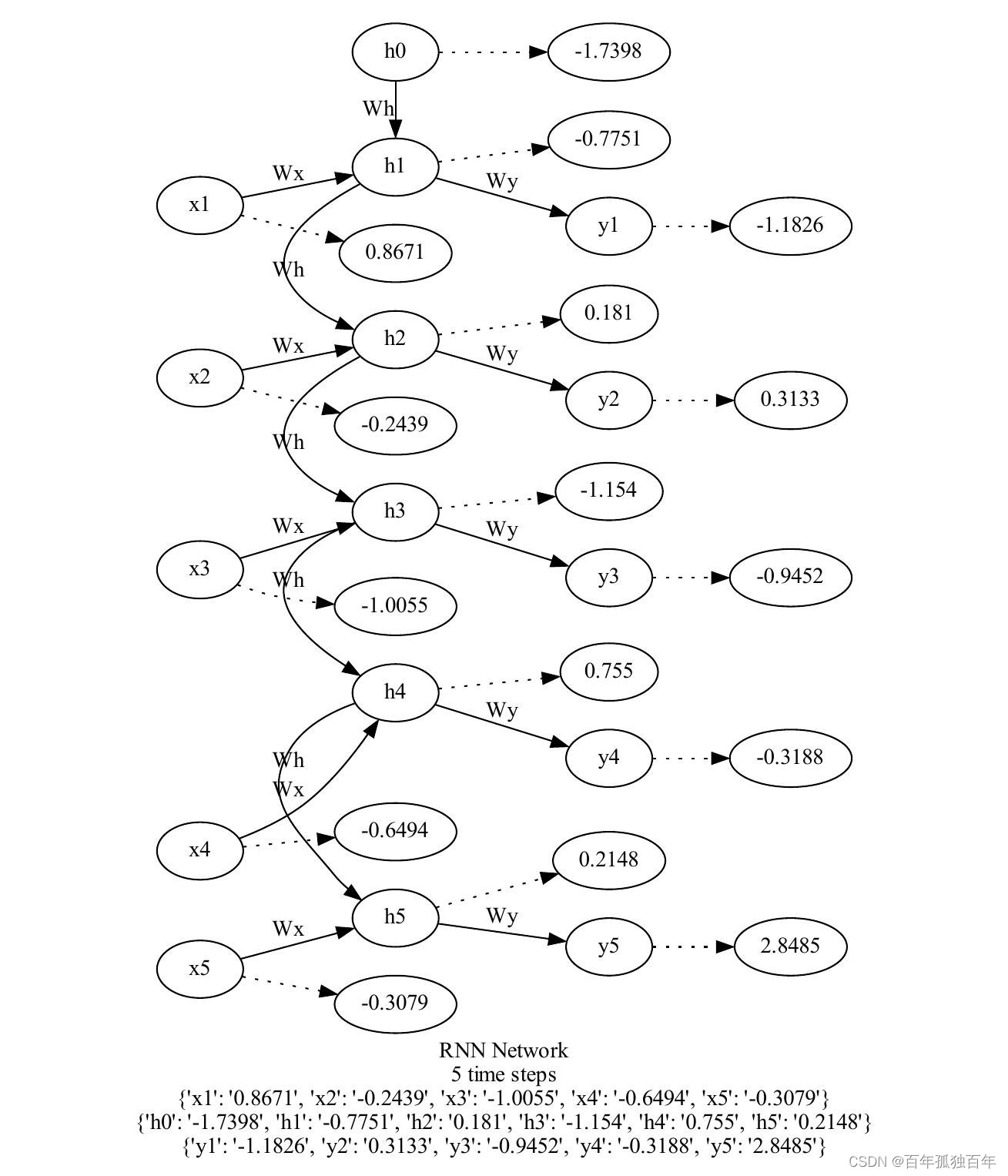
循环神经网络(RNN)简单介绍—包括TF和PyTorch源码,并给出详细注释
文章目录 循环神经网络(RNN)入门教程1. 循环神经网络的原理2. 循环神经网络的应用3. 使用keras框架实现循环神经网络3.1导入对应的库及加载数据集3.2.数据预处理3.3定义RNN模型3.4训练模型3.5测试模型 4.使用PyTorch框架实现上述功能—注释详细5.结论 循…...

Struts2 快速入门
Struts2 是一个基于 MVC 设计模式的 Java Web 应用程序框架,它可以帮助我们更加有效地开发 Web 应用程序。Struts2 采用了前端控制器模式,通过核心控制器 DispatchServlet 将所有请求进行集中处理,然后将请求分发到指定的 Action 中ÿ…...

关于PullToRefreshView下拉刷新失效问题
一、问题原因 昨天,突然一个问题丢在了我的头上,用户反馈说某某界面下拉刷新不好使啊,怎么回事。二话不说直接运行项目,经过测试,发现果然不好使。一看代码提交日期好家伙2020年,百思不得其解,…...

JAVA开发中的六大原则
JAVA开发中的六大原则,也被称为SOLID原则,是软件开发中常用的一组设计原则。这些原则提供了实现高质量、易于维护和可扩展软件的基本策略。 以下是JAVA开发中的六大原则以及它们的详细说明: 单一职责原则(Single Responsibility…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
