[LeetCode复盘] LCCUP‘23春季赛 20230422
[LeetCode复盘] LCCUP'23春季赛 20230422
- 一、总结
- 二、 1. 补给马车
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、2. 探险营地
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、 3. 最强祝福力场
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、 4. 传送卷轴
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、 5. 魔法棋盘(以后补)
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 七、参考链接
一、总结
- 半年前秋季赛3题,这次春季赛4题,有进步!
- T1 模拟。
- T2 模拟。
- T3 暴力枚举/扫描线。
- T4 最短路+二分。
- T5 状压DP。

二、 1. 补给马车
链接: 1. 补给马车
1. 题目描述

2. 思路分析
按题意模拟即可。
- py的话,可以直接切片赋值,非常方便。
- 复杂度n方。
3. 代码实现
class Solution:def supplyWagon(self, a: List[int]) -> List[int]:n = len(a)if n <= 3:return [sum(a)]d = n - n // 2 for _ in range(d):i = 0mx = a[0]+a[1]for j in range(1,len(a)-1):s = a[j]+a[j+1]if s < mx:mx = s i = j a[i:i+2] = [mx]return a
三、2. 探险营地
链接: 2. 探险营地
1. 题目描述

2. 思路分析
贴模板。
- 都乘到一起找质因数就是分别找质因数然后去重,因此用set记录并集即可。
3. 代码实现
class Solution:def adventureCamp(self, a: List[str]) -> int:s = set(x for x in a[0].split('->') if x)# print(s)ans = -1 mx = 0for i in range(1,len(a)):p = set(x for x in a[i].split('->') if x)x = len(s)s |= padd = len(s) - x if add > mx:mx = add ans = i return ans
四、 3. 最强祝福力场
链接: 3. 最强祝福力场
1. 题目描述

2. 思路分析
- 扫描线不会,但这题n=100,因此可以暴力。
- 由于最优矩形一定是切出来的,因此左边一定是某个矩形的左边,下边一定是某个矩形的下边。
- 那么最优矩形的左下角是可以枚举的。具体见代码。
- 枚举每个左下角,计算它在几个矩形里即可。
- 每个数据都乘2,避免浮点运算。
3. 代码实现
class Solution:def fieldOfGreatestBlessing(self, a: List[List[int]]) -> int:for i,(x,y,d) in enumerate(a):a[i] = (x*2,y*2,d*2)xx = []yy = []for x,y,d in a:xx.append(x-d//2)yy.append(y-d//2)ans = 1for x1 in xx:for y1 in yy:cnt = 0for x,y,d in a:if x-d//2<=x1<=x+d//2 and y-d//2<=y1<=y+d//2:cnt += 1ans = max(ans,cnt)return ans
五、 4. 传送卷轴
链接: 4. 传送卷轴
1. 题目描述

2. 思路分析
- 题目只问传送后到T的步数,因此可以直接先从T出发计算最短路,如果到不了S直接返回-1。
- 这个最短路作为玩家被传送后,带着debuff到T的步数。
- 魔王可以在s-t的任意格子上使玩家传送到镜像,注意,必须是玩家在’.‘(不包括S),镜像的位置必须是’.'/‘S’。
- 那么可以预处理每个位置的权值p,玩家经过这个位置的话,魔王的操作可以让玩家步骤变成max{镜像位置的dis},若这个位置不能进行传送,则p=0,因为只计算传送后的距离。
- 预处里完P后,玩家需要找一条s->t的连通路径,魔王可以选这个路径上的最大位置。那么玩家的目的就是最小化路径上的最大值。警觉,可以二分。
- 设这个最大值是x,那么路径上的所有值需要<=x,显然x越大越能满足;x越小越不可以满足。
- 或者可以dij,直接用堆,玩家每次都选最小的相邻位置并更新mx,走到T即可。代码会短一些
3. 代码实现
DIRS = [(0,1),(0,-1),(1,0),(-1,0)]
class Solution:def challengeOfTheKeeper(self, g: List[str]) -> int:m,n = len(g),len(g[0])dis = [[inf]*n for _ in range(m)]def inside(x,y):return 0<=x<m and 0<=y<n def find_t():for i in range(m):for j in range(n):if g[i][j] == 'T':return i,j def find_s():for i in range(m):for j in range(n):if g[i][j] == 'S':return i,j tx,ty = find_t()sx,sy = find_s()dis[tx][ty] = 0q = deque([(tx,ty)])while q:x,y = q.popleft()d = dis[x][y] + 1for dx,dy in DIRS:a,b = x+dx,y+dyif inside(a,b) and dis[a][b] > d and g[a][b] != '#':dis[a][b] = dq.append((a,b))if dis[sx][sy] == inf:return -1def get(x,y):if g[x][y] != '.':return 0 r = 0if g[x][n-y-1] != '#':r = max(r,dis[x][n-y-1])if g[m-x-1][y] != '#':r = max(r,dis[m-x-1][y])return rans = 0 top = 0p = [[inf]*n for _ in range(m)]for i in range(m):for j in range(n):if dis[i][j] < inf:p[i][j] = get(i,j)if p[i][j] < inf:top = max(top,p[i][j])q = [(0,sx,sy)]vis = [[False]*n for _ in range(m)]vis[sx][sy] = Truewhile q:d,x,y = heappop(q)ans = max(ans,d)for dx,dy in DIRS:a,b = x + dx, y + dyif a==tx and b ==ty:return ansif not inside(a,b) or g[a][b] == '#' or vis[a][b] or p[a][b] == inf:continuevis[a][b] = Trueheappush(q,(p[a][b],a,b))return -1# # 二分做法
# vis = [[-10]*n for _ in range(m)]
# # 是否存在路径,路径上的权值都<=x
# def ok(z):
# vis[sx][sy] = z
# def dfs(x,y):
# if x==tx and y == ty:
# return True
# for dx,dy in DIRS:
# a,b = x+dx,y+dy
# if not inside(a,b) or g[a][b] == '#':
# continue
# if p[a][b] > z:
# continue
# if a==tx and b == ty:
# return True
# if vis[a][b] != z:
# vis[a][b] = z
# if dfs(a,b):
# return True
# # print(x,y)
# return False# return dfs(sx,sy)
# # print(p)
# # print(ok(7))
# ans = bisect_left(range(top+1),True,key=ok)
# # print(top,ans) # if ans == top+1:
# return -1
# return ans
六、 5. 魔法棋盘(以后补)
链接: 5. 魔法棋盘
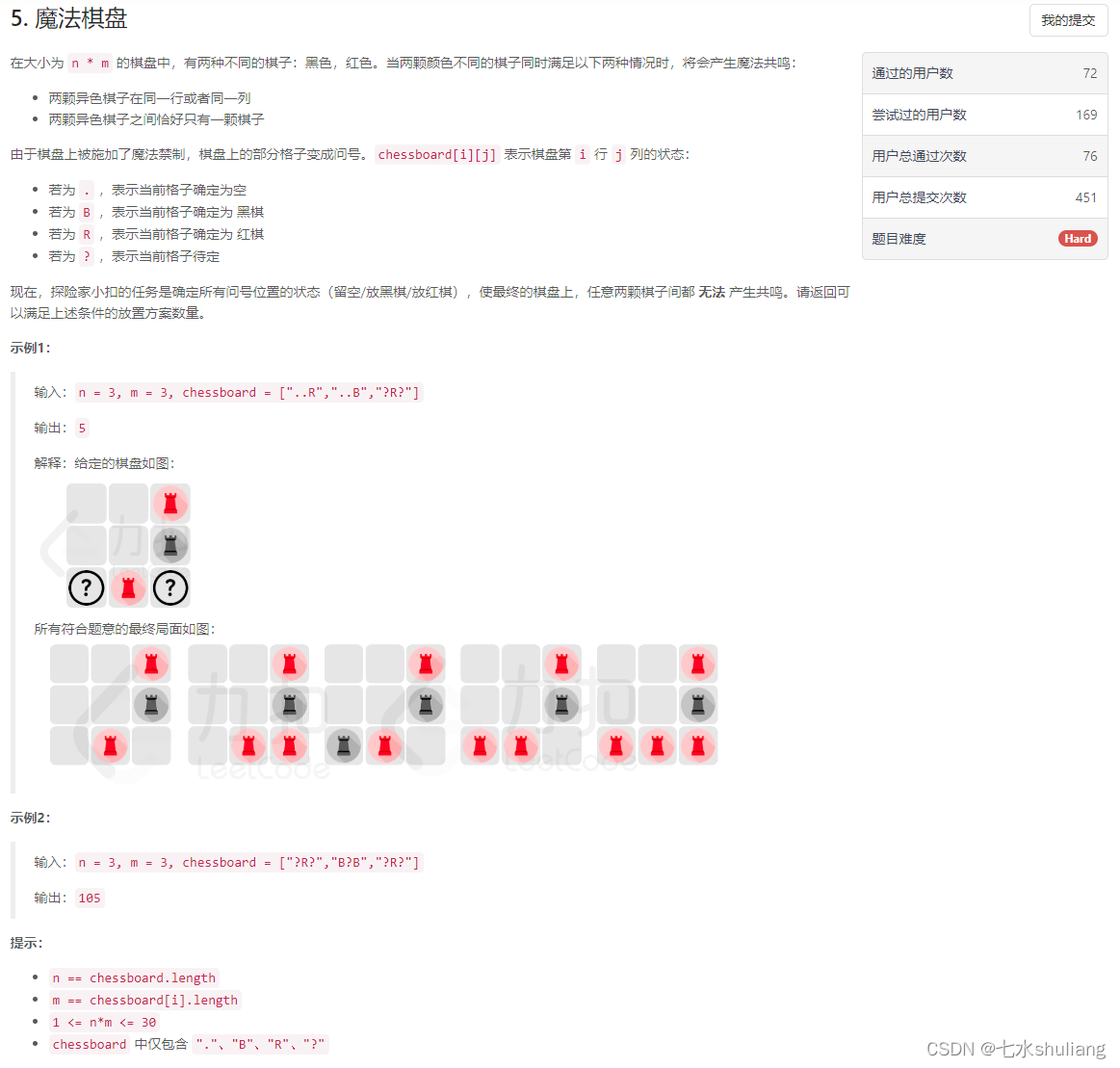
1. 题目描述
2. 思路分析
- 直接暴力状压,但是TLE了。想想也是,全问号的情况下,每个位置枚举空和R就2^30次方了。
- 等听完课再补。
3. 代码实现
class Solution:def getSchemeCount(self, n: int, m: int, g: List[str]) -> int: stat = []for i in range(n):for j in range(m):stat.append(g[i][j])@cache def dfs(i,stat):if i == n*m:return 1if stat[i] != '?':return dfs(i+1,stat) def check(a): # check一个一个方向上的一条是否合法z = []for c in a:if c in 'RB?':z.append(c)if len(z) <= 2:return True# if len(set(z)) == 1:# return True for i in range(2,len(z)):x,y = z[i],z[i-2]if x != y and x != '?' and y !='?' and z[i-1] !='?': return Falsereturn Truedef ok(x,y): # check这个点所在的行列是否合法a =[]for i in range(n):if p[i][y] in 'RB?':a.append(p[i][y])if len(a)>=3 and a[-1]!='?' and a[-2]!='?' and a[-3]!='?' and a[-1]!=a[-3]:return False a = []for j in range(m):if p[x][j] in 'RB?':a.append(p[x][j])if len(a)>=3 and a[-1]!='?' and a[-2]!='?' and a[-3]!='?' and a[-1]!=a[-3]:return Falsereturn Truep = [['']*m for _ in range(n)] # 还原出棋盘s = list(stat)for x in range(n):for y in range(m):p[x][y] = s[x*m + y]ans = 0 x,y = divmod(i,m)for c in 'RB.':p[x][y] = cif ok(x,y) :s[i] = cans += dfs(i+1,tuple(s)) return ans return dfs(0,tuple(stat))
七、参考链接
相关文章:

[LeetCode复盘] LCCUP‘23春季赛 20230422
[LeetCode复盘] LCCUP23春季赛 20230422 一、总结二、 1. 补给马车1. 题目描述2. 思路分析3. 代码实现 三、2. 探险营地1. 题目描述2. 思路分析3. 代码实现 四、 3. 最强祝福力场1. 题目描述2. 思路分析3. 代码实现 五、 4. 传送卷轴1. 题目描述2. 思路分析3. 代码实现 六、 5…...

传统燃油车的智控App远控响应速度优化方向几点思考
一、分析当前问题及其影响因素 网络延迟:燃油车的App远控响应速度受到网络延迟的影响。网络延迟可能是由于网络拥堵或服务器响应速度慢等原因导致的。 用户设备:用户设备的性能也会影响燃油车的App远控响应速度。例如,设备的内存不足或存在故…...
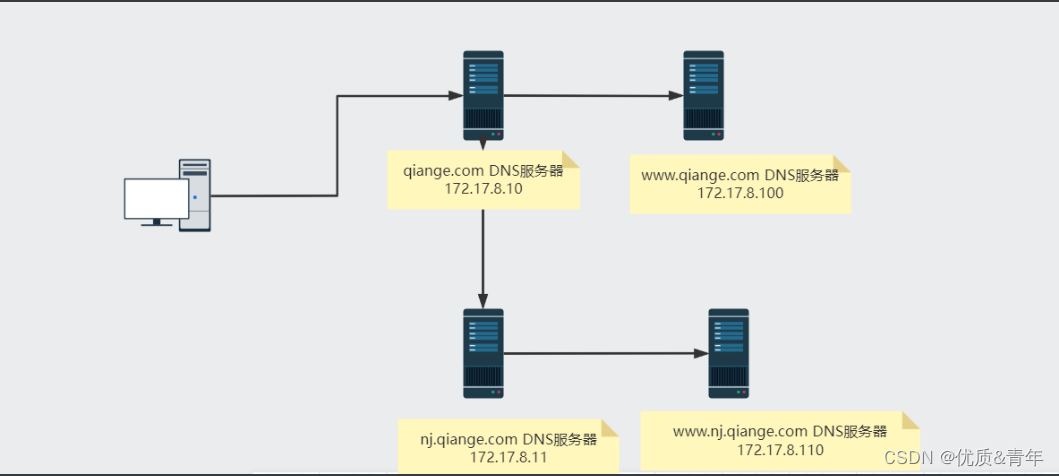
回炉重造九---DNS服务器
1、DNS服务器的相关概念和技术 1.1 DNS服务器的类型 主DNS服务器从DNS服务器缓存DNS服务器(forward DNS服务器{转发器}) 1.1.1 主DNS服务器的作用 管理和维护所负责解析的域内解析库的服务器1.1.2 从DNS服务器的作用 从主服务器或从服务器“复制”解…...
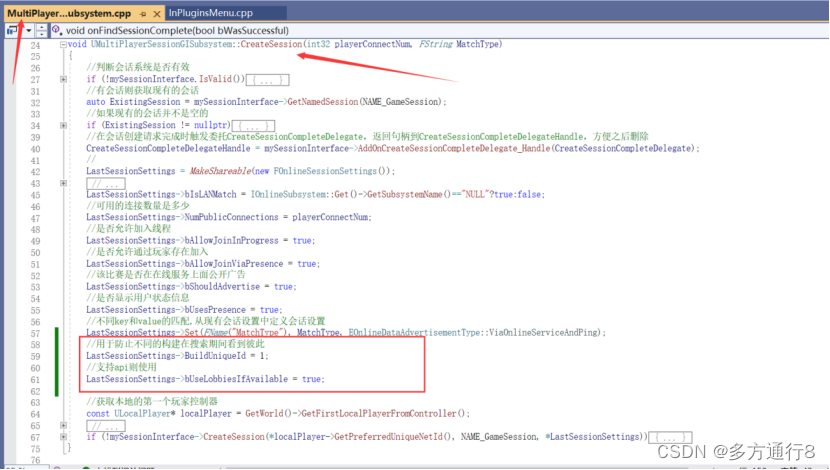
UE4/5多人游戏详解(七、自定义委托,实现寻找会话和加入会话的函数,通过Steam进行两台电脑的联机)
目录 可能出现问题(在六部分的测试可能无法连接的问题【在末尾加上了,怕有人没看见在这里写一下】) 自定义委托 调整位置 创建更多的委托和回调函数给菜单: 多播和动态多播 代码: 委托变量 代码: 回…...
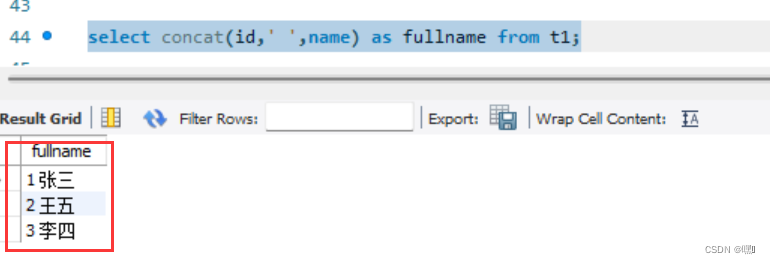
【数据库多表操作】sql语句基础及进阶
常用数据库: 数据库(Database)是按照数据结构来组织、存储和管理数据的仓库,它是长期存储在计算机内、有组织、有结构的数据集合。数据库是信息系统的核心部分,现代软件系统中大量采用了数据库管理系统(DBM…...

DPDK和RDMA的区别
网络的发展好像在各方面都是滞后于计算和存储,时延方面也不例外,网络传输时延高,逐渐成为了数据中心高性能的瓶颈。因为传统两个节点间传输数据的网络路径上有大量的内存拷贝,导致网络传输效率低下,网络数据包的收发处…...

体验 Google Bard
环境 windows 10 64bitGoogle Bardpython 3.8 简介 本篇介绍一个开源的 Google 聊天机器人Bard 的 API 逆向工程,使用它,可以免费的使用 Bard 服务,项目地址:https://github.com/acheong08/Bard 安装及使用 通过 pip 来安装 pip &…...

MITA触摸屏维修WP4053米塔工控机控制屏维修
MITA-TEKNIK米塔触摸屏维修工控机工控屏控制器维修DISPLAY 2COM全系列型号 Mita-Teknik触摸屏维修常见故障:上电无显示,运行报故障,无法与电脑通讯,触摸无反应,触控板破裂,触摸玻璃,上电黑屏&a…...
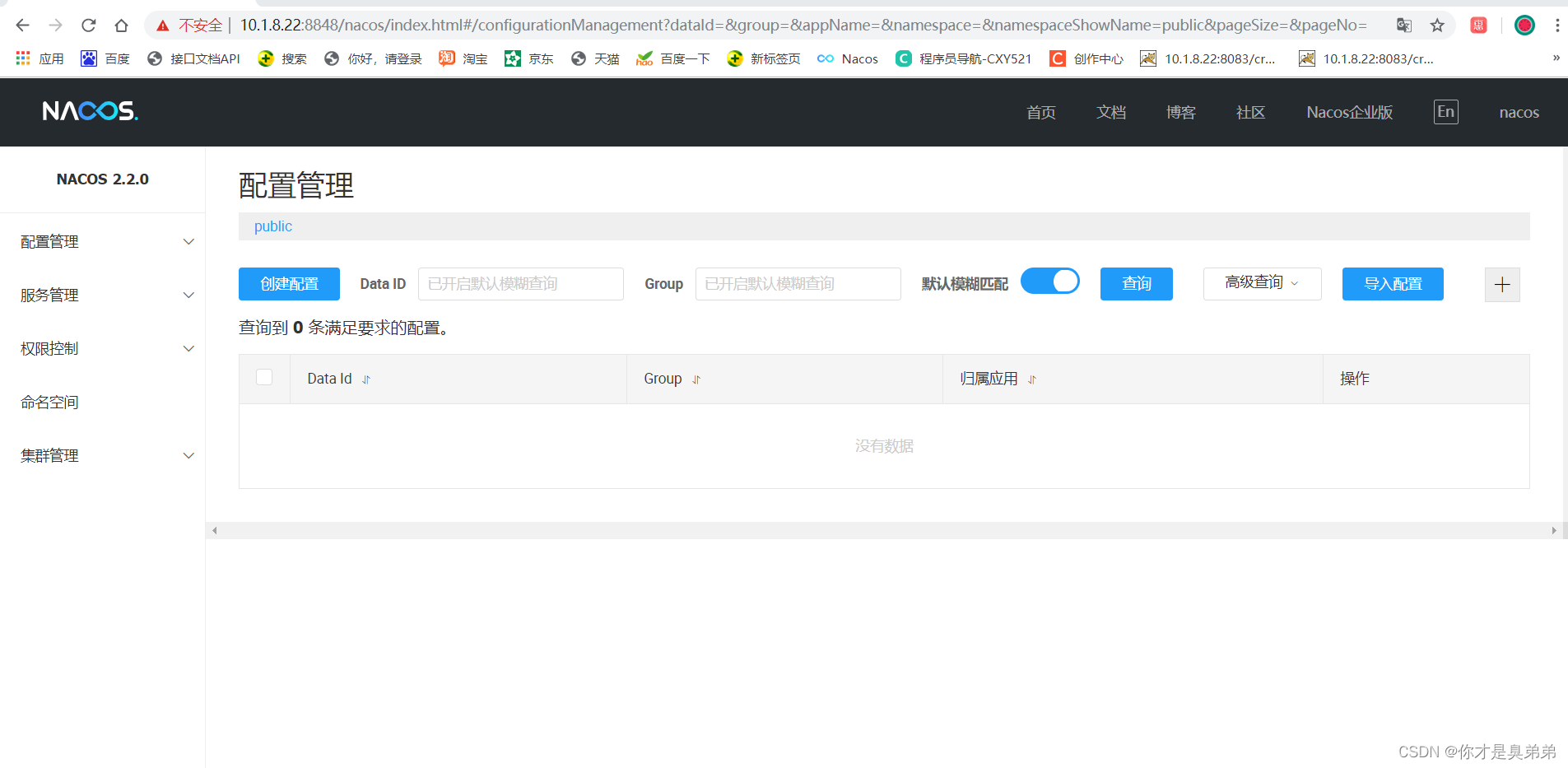
Nacos简介 安装 配置
简介 什么是注册中心 注册中心在微服务项目中扮演着非常重要的角色,是微服务架构中的纽带,类似于通讯录,它记录了服务和服务地址的映射关系。在分布式架构中,服务会注册到这里,当服务需要调用其它服务时,…...
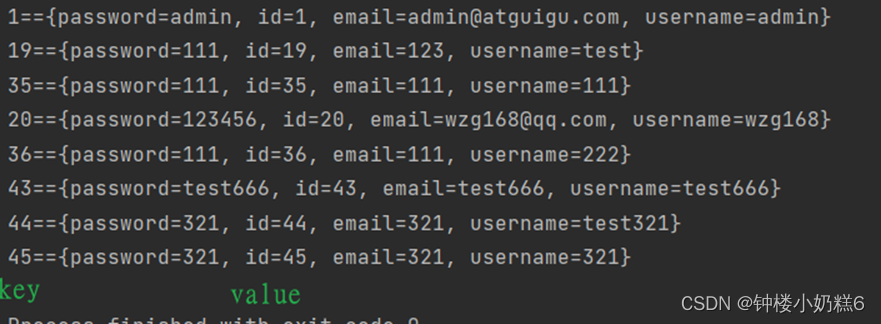
五、MyBatis各种查询功能
MyBatis的各种查询功能 如果查询出的数据只有一条,可以通过 实体类对象接收List集合接收Map集合接收 如果查询出的数据有多条,一定不能用实体对象接收,会抛TooManyResultsException,可以通过 实体类类型的List集合接收Map类型…...

uni-app——picker组件的用法、时间、日期、地区选择器等
1、uniapp–picker组件 <template><view class"signUp"><view class"signUp_dv1"><u-form :model"form" ref"uForm" label-width"95px"><u-form-item label"日期" :required"tr…...

什么情况需要考虑 mysql 分表
最近看到公司的其中一个数据库用户表每个月都要几百万的新用户数据增加,目前单表已经是两千多万了。所以找了 DBA 讨论,发现以前学的知识,以及网上的一些资料其实说的并不是很正确,比如 mysql 单表不建议超过一千万,我…...

系统架构师02-架构设计 20分
1.架构基本概念 *质量属性效用树:是对系统质量属性进行识别和优先级排序的重要工具 。 包括: 性能:效率指标,处理任务所需时间或单位时间内的处理量。 可用性: 可靠性: 容错:出现错误后人能保…...
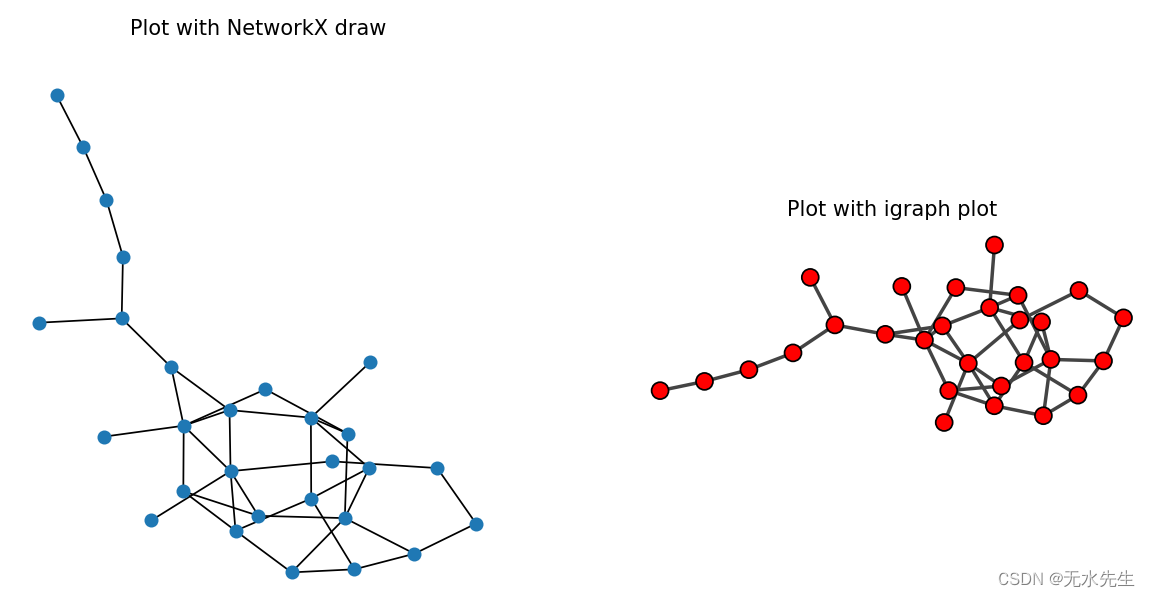
【python视图3】networkx图操作示例
一、说明 根据定义,图是节点(顶点)以及已识别的节点对(称为边、链接等)的集合。在 NetworkX 中,节点可以是任何可哈希对象,例如文本字符串、图像、XML 对象、另一个图形、自定义节点对象等。 如…...
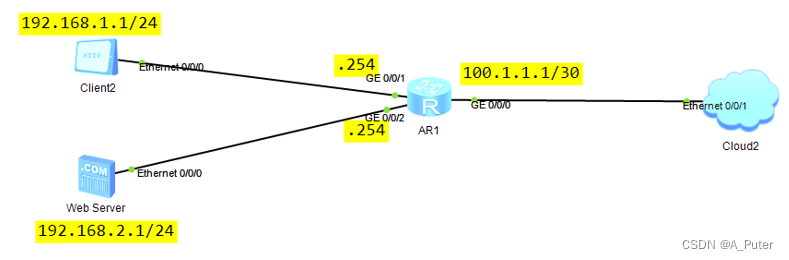
网络地址转换应用
如图所示,企业使用一台AR 路由器作为出口设备,路由器配置NAT Outbound为私网用户提供访问Internet服务,同时配置NAT Server将私网WEB服务器发布到公网上,对外网用户提供服务。运营商仅为该单位分配了一个公网IP,此地址既作为AR出接口的IP地址,也作为NAT Outbound和NAT Se…...
强化学习-Double DQN、竞争网络结构和Rainbow(第4章)
来源书籍: TENSORFLOW REINFORCEMENT LEARNING QUICK START GUIDE 《TensorFlow强化学习快速入门指南-使用Python动手搭建自学习的智能体》 著者:[美]考希克巴拉克里希南(Kaushik Balakrishnan) 译者:赵卫东 出版…...

Unity 性能优化锦集
Unity作为一款主流的游戏开发引擎,不仅提供了强大的编辑器和开发工具,还可以让开发者轻松地实现高质量的3D游戏。但是,随着游戏规模的不断扩大和玩家需求的增加,游戏的性能问题也变得越来越重要。因此,在使用Unity进行…...
JS之Map的基本使用
一、Map的基本API 创建: const map new Map()插入:map.set("name", "郑建")读取:map.get("name")判断:map.has("name")删除:map.delete大小:map.size遍历&#…...
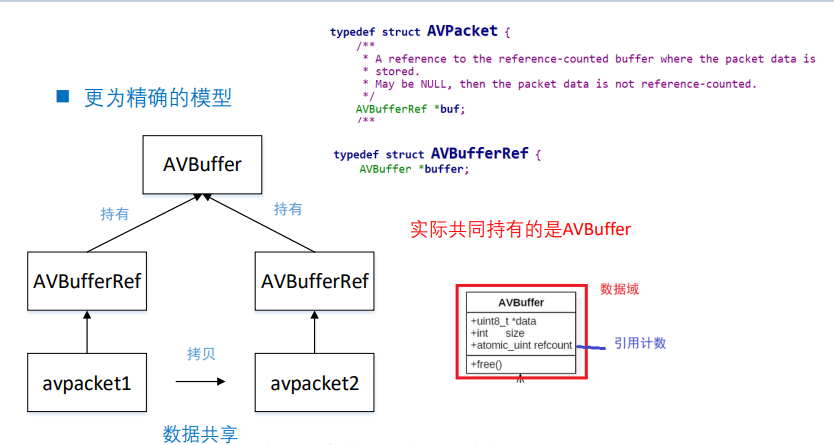
音视频八股文(6)-- ffmpeg大体介绍和内存模型
播放器框架 常用音视频术语 • 容器/文件(Conainer/File):即特定格式的多媒体文件, 比如mp4、flv、mkv等。 • 媒体流(Stream):表示时间轴上的一段连续数据,如一 段声音…...

4.25~~~~~
接着之前PE文件结构的预习 DOS 定位到NT 怎么操作的? 用的是e_lfanew,然后是相对于文件头的偏移量(也就是raw表示方法) 现在有个问题,为什么e_lfanew 这个变量不直接存储PE头 的绝对地址呢? 比如说&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
