偏好强化学习概述
文章目录
- 为什么需要了解偏好强化学习
- 什么是偏好强化学习
- 基于偏好的马尔科夫决策过程(Markov decision processes with preferences,MDPP)
- 反馈类型分类
- 学习算法分类
- 近似策略分布(Approximating the Policy Distribution)
- 比较和排序策略(Comparing and Ranking Policies)
- 学习偏好模型(Learning a Preference Model)
- 学习奖励函数(Learning a Utility Function)
- 近期工作
- Deep Reinforcement Learning from Human Preference(2023)
- Preference Transformer: Modeling Human Preferences using Transformers for RL(2023)
- 更多相关文章
为什么需要了解偏好强化学习
为什么需要了解偏好强化学习?目前强化学习主流的方法都是基于奖励的,强化学习优化目标是长期的累计奖励。而如何设计一个好的奖励函数通常需要大量专家领域知识。并且需要考虑提出的奖励函数是否会影响学习过程,比如学习速度等等问题。在有些场景也并不是能够很好地去定义出这样一个奖励。
对于实际业务问题,业务本身比较复杂,传统解决方法(比如行为树)如果不好,那也不能基于数据去做一些offline RL。并且如果不好给定奖励函数的话,通常会采用模仿学习的方法。但是也存在一些场景人类专家也不能给出一些确切的行为,因此也不能去做一些模仿学习,比如在机器人领域控制电机的电流进而控制机械臂,人类专家无法直接给出电流的参考示例。直接人类给出动作的代价相比于给出偏好的代价是更高的。还有一些场景动作空间巨大,比如电网调度领域,动作空间高达几万个等等的一些传统解决方案很棘手的场景中,可以考虑去采用偏好强化学习来作为一种初始化网络参数,或者微调修复性能的方法。
随着生产物质的丰富,用户对于个性化追求将愈发强烈。如何将用户的个性化偏好进行量化,进而更好地服务用户(比如用GPT作为智能家居中控,给用户提供个性化的全家智能)。比如在游戏AI领域,如何基于用户反馈,设计出拟人性的智能体,或者是符合玩家兴趣爱好的智能体,或者依据玩家偏好变化而变化的NPC都是未来的发展趋势。
什么是偏好强化学习
想要去解决一个问题,首先需要去寻找的就是优化目标。在强化学习里面的优化目标就是奖励函数,因此想要待解决的问题用强化学习方法来求解,就需要将优化目标与奖励函数挂钩。而基于专家经验设计的奖励函数通常会面临四个问题:1. Reward Hacking: 只管最大化奖励分数,不考虑实际情况。2. Reward Shaping: 平衡goal definition和guidance task。3. Infinite Rewards: 存在一些case,是坚决不允许发生的。虽然现在有mask可以去做,但是也有一些问题其实是没有办法用mask去做的,只有做了之后才能验证是否违反了硬约束条件。4. Multi-objective Trade-off: 如果需要考虑多个优化目标
当然也有一些方法在设计一些内在的奖励,来处理这样一个问题。然而设计一个好的内在奖励其实也是很困难的。
偏好强化学习(Preference-Based Reinforcement Learning, PbRL)直接基于专家的反馈进行学习,并不需要设计奖励函数,并且对于人类对于专业领域的需求也比较少,因为给一个确切的数值奖励给智能体,而是一个比较值。PbRL的关键在于说把强化学习里面,对于奖励,从一个数值的反馈信号变成了一个偏好的反馈信号。想要构建偏好强化学习的优化过程,我们还需要去定义一些符号,和我们能够拿到的数据集合:
- z i ≻ z j z_{i} \succ z_{j} zi≻zj: 数据 z i z_{i} zi是strictly preferred。
- z i ∼ z j z_{i} \sim z_{j} zi∼zj: 数据偏好是无法区分的 indifferent。
- z i ⪰ z j z_{i} \succeq z_{j} zi⪰zj: 数据 z i z_{i} zi是weakly preferred。
基于偏好的马尔科夫决策过程(Markov decision processes with preferences,MDPP)
一个MDPP可以定义成 ( S , A , μ , δ , γ , ρ ) (S, A, \mu, \delta, \gamma, \rho) (S,A,μ,δ,γ,ρ):
- S S S 状态空间
- A A A 动作空间
- μ ( s ) \mu(s) μ(s) 初始状态分布
- δ \delta δ 状态转移模型 δ ( s ′ ∣ s , a ) \delta(s^{\prime} | s, a) δ(s′∣s,a)
- γ \gamma γ 折扣因子
一条采样的轨迹(trajectory)可以表示为:
τ = { s 0 , a 0 , s 1 , a 1 , … , s n − 1 , a n − 1 , s n } \boldsymbol{\tau}=\{s_0,a_0,s_1,a_1,\ldots,s_{n-1},a_{n-1},s_n\} τ={s0,a0,s1,a1,…,sn−1,an−1,sn}
ρ ( τ i ≻ τ j ) \rho(\tau_{i} \succ \tau_{j}) ρ(τi≻τj)定义为给定轨迹 ( τ i , τ j ) (\tau_{i}, \tau_{j}) (τi,τj)下, τ i ≻ τ j \tau_{i} \succ \tau_{j} τi≻τj的概率。智能体可以接收到一个偏好集合:
ζ = { ζ i } = { τ i 1 ≻ τ i 2 } i = 1... N \zeta=\{\zeta_i\}=\{\tau_{i1}\succ\tau_{i2}\}_{i=1...N} ζ={ζi}={τi1≻τi2}i=1...N
并且假设偏好是严格偏好,也就是有:
ρ ( τ i ≻ τ j ) = 1 − ρ ( τ j ≻ τ i ) \rho(\boldsymbol\tau_i \succ \boldsymbol\tau_j) = 1 - \rho(\boldsymbol{\tau}_j \succ \boldsymbol{\tau}_{i}) ρ(τi≻τj)=1−ρ(τj≻τi)
注意:这里并没有假设一个奖励的数值信号 r ( s , a ) r(s, a) r(s,a)。
如何基于人类反馈的偏好来优化策略呢?
基于人类反馈的优化框架如下图所示:
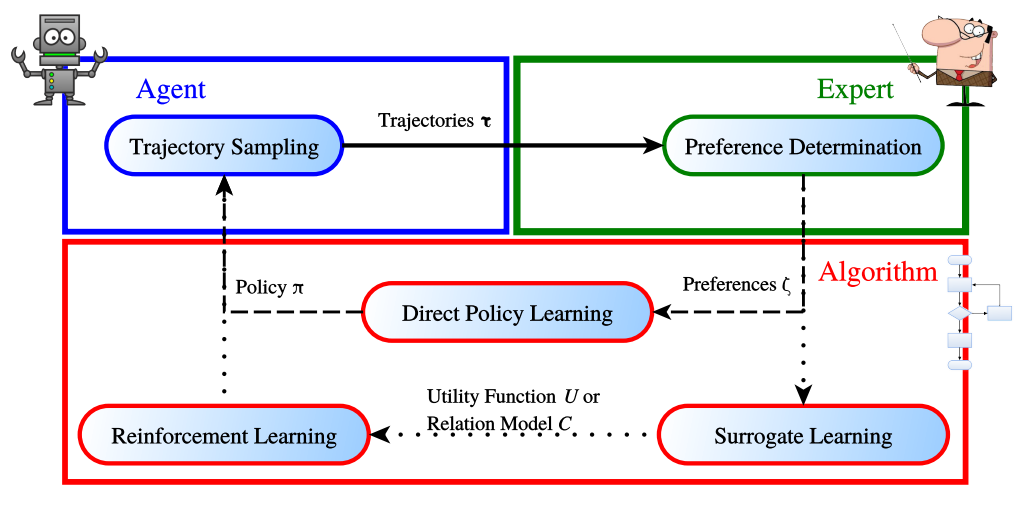
对于一个智能体来说,一个通用的目标是,在一个给定的集合 ζ \zeta ζ中去寻找到一个策略 π ∗ \pi^{*} π∗,能够最大化人类偏好。 τ 1 ≻ τ 2 ∈ ζ \tau_{1} \succ \tau_{2} \in \zeta τ1≻τ2∈ζ需要满足的条件是:
τ 1 ≻ τ 2 ⇔ Pr π ( τ 1 ) > Pr π ( τ 2 ) \boldsymbol{\tau_1}\succ \boldsymbol{\tau_2}\Leftrightarrow\operatorname*{Pr}_\pi(\boldsymbol{\tau}_1)>\operatorname{Pr}_\pi({\boldsymbol\tau}_2) τ1≻τ2⇔πPr(τ1)>Prπ(τ2)
其中
Pr π ( τ ) = μ ( s 0 ) ∏ t = 0 ∣ τ ∣ π ( a t ∣ s t ) δ ( s t + 1 ∣ s t , a t ) \Pr_{\pi}(\boldsymbol{\tau})=\mu(s_0)\prod\limits_{t=0}^{|\boldsymbol{\tau}|}\pi(a_t\mid s_t)\delta(s_{t+1}\mid s_t,a_t) πPr(τ)=μ(s0)t=0∏∣τ∣π(at∣st)δ(st+1∣st,at)
基于轨迹(trajectory)的最大化偏好问题可以描述为:
τ 1 ≻ τ 2 ⇔ π ∗ = arg max π ( Pr π ( τ 1 ) − Pr π ( τ 2 ) ) \pmb\tau_1\succ\pmb\tau_2\Leftrightarrow\pi^*=\arg\max\limits_{\pi}\left(\Pr_\pi(\pmb\tau_1)-\Pr_\pi(\pmb\tau_2)\right) τ1≻τ2⇔π∗=argπmax(πPr(τ1)−πPr(τ2))
到此,我们就可以定义出一个最小化偏好损失函数:
L ( π , τ 1 ≻ τ 2 ) = − ( Pr π ( τ 1 ) − Pr π ( τ 2 ) ) L(\pi,\boldsymbol{\tau_1} \succ \boldsymbol{\tau_2}) = - \left(\Pr_\pi(\boldsymbol{\tau}_1) -\Pr_\pi({\boldsymbol\tau_2})\right) L(π,τ1≻τ2)=−(πPr(τ1)−πPr(τ2))
在有多个偏好相互比较的关系下,损失函数可以表示为:
L ( π , ζ ) = ( L ( π , ζ 0 ) , L ( π , ζ 1 ) , … , L ( π , ζ n ) ) \boldsymbol{L}(\pi,\zeta)=(L(\pi,\zeta_{0}),L(\pi,\zeta_1),\dots,L(\pi,\zeta{_n})) L(π,ζ)=(L(π,ζ0),L(π,ζ1),…,L(π,ζn))
表示为权重加和的方式则为:
L ( π , ζ ) = ∑ i = 1 N α i L ( π , ζ i ) \mathcal{L}(\pi,\zeta)=\sum_{i=1}^N\alpha_i L(\pi,\zeta_i) L(π,ζ)=i=1∑NαiL(π,ζi)
反馈类型分类
- 动作偏好(action preference): 对于给定的相同状态,比较两个动作。这种方法无法处理短期偏好与长期偏好的关系。
- 状态偏好(state preference): s i 1 ≻ s i 2 s_{i1} \succ s_{i2} si1≻si2表示相比于状态 s i 2 s_{i2} si2,人类更偏好状态 s i 1 s_{i1} si1。
- 轨迹偏好(trajectory preference): τ i 1 ≻ τ i 2 \tau_{i1} \succ \tau_{i2} τi1≻τi2表示轨迹 τ i 1 \tau_{i1} τi1优于轨迹 τ i 2 \tau_{i2} τi2。轨迹偏好里一个重要问题就是信用分配问题(temporal credit assignment problem)。
学习算法分类
近似策略分布(Approximating the Policy Distribution)
对于给定的trajectory ζ \zeta ζ,基于参数化的策略分布 Pr ( π ∣ ζ ) \Pr(\pi | \zeta) Pr(π∣ζ)产生不同的策略 π 1 , π 2 \pi_{1}, \pi_{2} π1,π2,再基于产生的不同的策略来产生不同的trajector τ 1 , τ 2 \tau_{1}, \tau_{2} τ1,τ2, 再给定人类评判偏好,存储偏好轨迹。最后产生能够最大化轨迹偏好的策略 a r g m a x π P r ( π ∣ ζ ) argmax_{\pi}Pr(\pi | \zeta) argmaxπPr(π∣ζ)。

比较和排序策略(Comparing and Ranking Policies)
给定策略集合,在策略集合中直接进行偏好排序,选取获取偏好排序最大的策略作为最终策略进行输出:

学习偏好模型(Learning a Preference Model)
直接学一个偏好模型: C ( a ≻ a ′ ∣ s ) C(a \succ a^{\prime} | s) C(a≻a′∣s),策略为贪婪策略。类似DQN,在这里是直接计算偏好函数,然后基于偏好函数来直接求解策略。

学习奖励函数(Learning a Utility Function)
基于偏好计算一个奖励函数 U ( τ ) U(\tau) U(τ),在许多场景中可以拆分为 U ( s , a ) U(s, a) U(s,a)。策略求解即为最大化奖励的过程。 这也是目前主流的求解方案:

总结这四类方法就是:1. 构建一个产生策略的函数 θ \theta θ,一最大化偏好轨迹来优化 θ \theta θ。2. 给定一个策略集合,基于偏好,直接在策略集合中选取能够产生人类偏好最大的策略。3. 学习一个偏好模型 C ( a ≻ a ′ ∣ s ) C(a \succ a^{\prime} | s) C(a≻a′∣s), 基于这个偏好模型直接贪婪产生策略。4. 学习奖励函数,策略基于奖励函数进行优化。
近期工作
Deep Reinforcement Learning from Human Preference(2023)
- Deep Reinforcement Learning from Human Preference
这篇文章主要贡献是用于比较困难的游戏场景中:

奖励预测器损失函数可以表示为:
P ^ [ σ 1 ≻ σ 2 ] = exp ∑ r ^ ( a t 1 , a t 1 ) exp ∑ r ^ ( o t 1 , a t 1 ) + exp ∑ r ^ ( o t 2 , a t 2 ) \hat{P}\bigl[\sigma^1\succ\sigma^2\bigr]=\frac{\exp\sum\hat{r}\bigl(a_t^1,a_t^1\bigr)}{\exp\sum\hat{r}(o^1_t,a_t^1)+\exp\sum{\hat{r}(o_t^2,a_t^2)}} P^[σ1≻σ2]=exp∑r^(ot1,at1)+exp∑r^(ot2,at2)exp∑r^(at1,at1)
log ( r ^ ) = − ∑ ( σ 1 , σ 2 , μ ) ∈ D μ ( 1 ) log P ^ [ σ 1 ≻ σ 2 ] + μ ( 2 ) log P ^ [ σ 2 ≻ σ 1 ] \log(\hat r)=-\sum_{(\sigma^1,\sigma^2,\mu)\in\mathcal D}\mu(1)\log\hat P\big[\sigma^1\succ\sigma^2\big]+\mu(2)\log\hat P\bigl[\sigma^2\succ\sigma^1\bigr] log(r^)=−(σ1,σ2,μ)∈D∑μ(1)logP^[σ1≻σ2]+μ(2)logP^[σ2≻σ1]
人类偏好的不稳定性,会导致奖励预测器的偏差和方差都受到一定的影响。
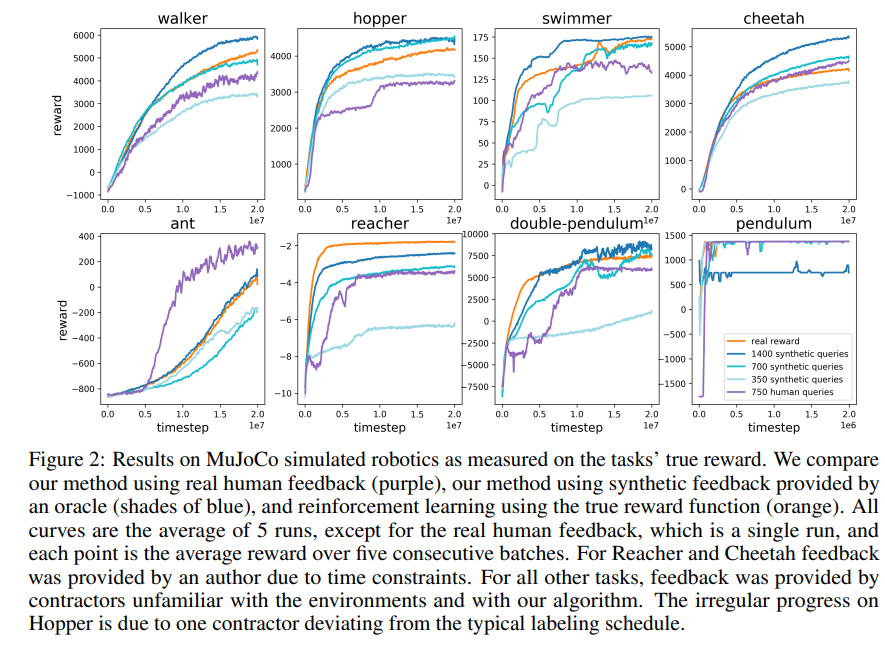
实验结果:
Preference Transformer: Modeling Human Preferences using Transformers for RL(2023)
- Preference Transformer: Modeling Human Preferences using Transformers for RL
这篇文章主要用于解决非马尔科夫性
整体框架图:
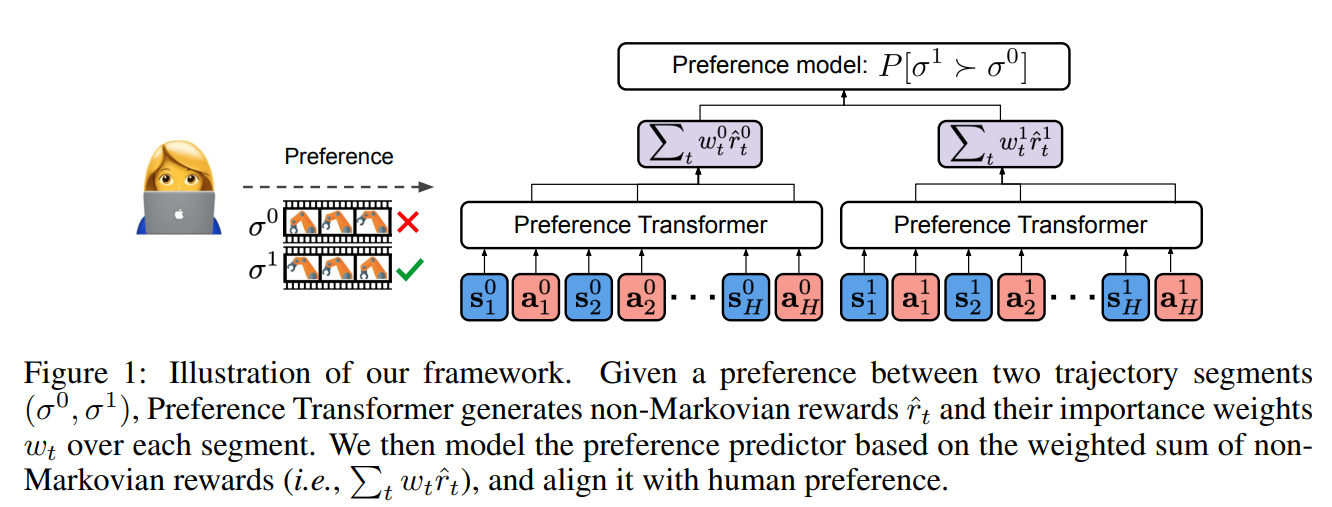
Preference Transformer局部:
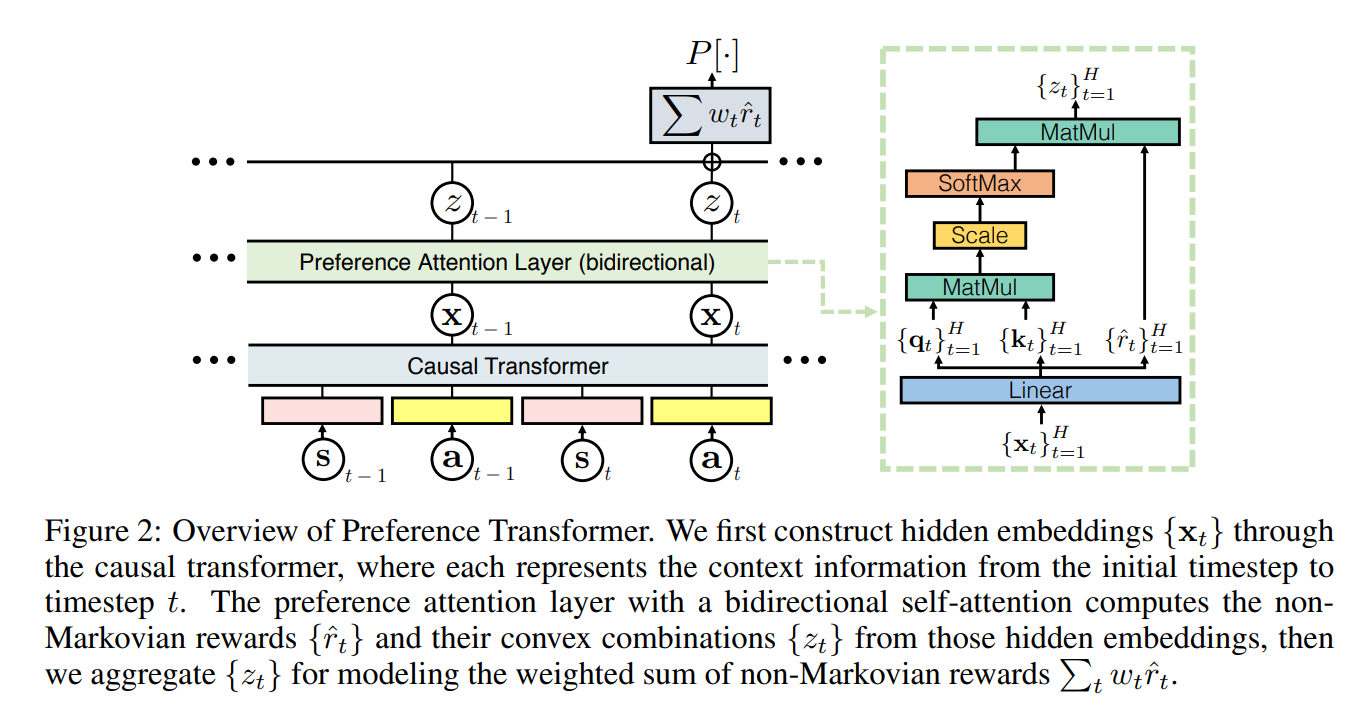
注意奖励在Linear层就已经进行了预测,后续输出是对trajectory奖励的加权。
在实验部分,作者设计了一系列的评估指标,用于确定Preference Transformer确实是学到了中间的关键步骤奖励,也就是确实进行了置信分配。
更多相关文章
- Tencent AI Lab:DEPLOYING OFFLINE REINFORCEMENT LEARNING WITH HUMAN FEEDBACK(2023)
- UC Berkeley:Principled Reinforcement Learning with Human Feedback from Pairwise or K-wise Comparisons(2023)
- OpenAI: Deep reinforcement learning from human preferences (2023)
- UC Berkeley:Preference Transformer: Modeling Human Preferences using Transformers for RL(2023)
- DeepMind: Improving Multimodal Interactive Agents with Reinforcement Learning from Human Feedback(2022)
- Humans are not Boltzmann Distributions: Challenges and Opportunities for Modelling Human Feedback and Interaction in Reinforcement Learning(2022)
- Google:Offline Reinforcement Learning from Human Feedback in Real-World Sequence-to-Sequence Tasks(2021)
- Explore, Exploit or Listen: Combining Human Feedback and Policy Model to Speed up Deep Reinforcement Learning in 3D Worlds (2021)
- Human feedback in continuous actor-critic reinforcement learning(2019)
- Stanford: Deep Reinforcement Learning from Policy-Dependent Human Feedback (2019)
- A Survey of Preference-Based Reinforcement Learning Methods (2017)
- Nature: Reinforcement learning improves behaviour from evaluative feedback(2015)
- Augmenting Reinforcement Learning with Human Feedback(2011)
相关文章:

偏好强化学习概述
文章目录 为什么需要了解偏好强化学习什么是偏好强化学习基于偏好的马尔科夫决策过程(Markov decision processes with preferences,MDPP) 反馈类型分类学习算法分类近似策略分布(Approximating the Policy Distribution)比较和排序策略(Comp…...

苹果笔到底有没有必要买?苹果平板电容笔排行榜
事实上,Apple Pencil与市场上普遍存在的电容笔最大的区别,就是两者的重量以及所具有的压感都互不相同。但是,苹果原有的电容笔因其昂贵的价格而逐步被平替电容笔所替代,而平替电容笔所具备的各种性能也在逐步提高。接下来…...
learn_C_deep_6 (布尔类型、布尔与“零值“、浮点型与“零值“、指针与“零值“的比较)
目录 语句和表达式的概念 if语句的多种语法结构 注释的便捷方法(环境vs) if语句执行的过程 逻辑与&& 逻辑或|| 运算关系的顺序 else的匹配原则 C语言有没有布尔类型 C99标准 sizeof(bool)的值为多少? _Bool原码 BOOL…...
JavaScript日期库之date-fn.js
用官网的话来说,date-fn.js 就是一个现代 JavaScript 日期实用程序库,date-fns 为在浏览器和 Node.js 中操作 JavaScript 日期提供了最全面、但最简单和一致的工具集。那实际用起来像它说的那么神奇呢,下面就一起来看看吧。 安装 安装的话就…...

五一假期出游攻略【诗与远方】
原文在:PUSDN 可以导入作为模板引用。 五一旅行计划 假期倒计时 [该类型的内容暂不支持下载] 本次目标:五一旅行计划【画饼版】 前言 任何一个地方,一个城市,都有可观赏的地方,如果没去过邢台的,建议五一去…...
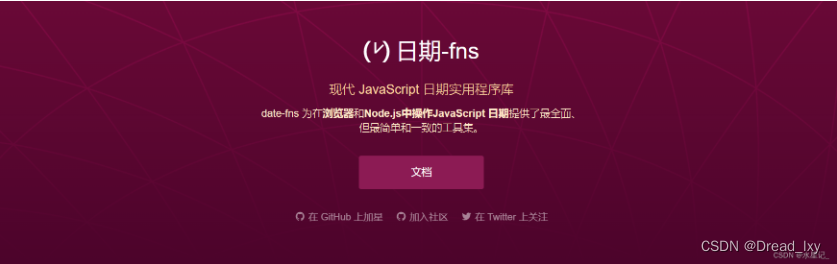
怎样正确做web应用的压力测试?
web应用,通俗来讲就是一个网站,主要依托于浏览器实现其功能。 提到压力测试,我们想到的是服务端压力测试,其实这是片面的,完整的压力测试包含服务端压力测试和前端压力测试。 下文将从以下几部分内容展开:…...

Hibernate的持久化类
Hibernate是一个开源的ORM(对象关系映射)框架,用于将Java程序中的对象映射到数据库中的关系型数据。在Hibernate中,持久化类是用来映射Java对象和关系型数据库表的类。 编写Hibernate持久化类需要遵循以下规则: 持久…...
【c语言】enum枚举类型的定义格式 | 基本用法
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...

Python数据挖掘与机器学习
近年来,Python编程语言受到越来越多科研人员的喜爱,在多个编程语言排行榜中持续夺冠。同时,伴随着深度学习的快速发展,人工智能技术在各个领域中的应用越来越广泛。机器学习是人工智能的基础,因此,掌握常用…...

Java有用的书籍2
. 1.《Effective Java》是由Joshua Bloch撰写的一本Java编程规范和最佳实践指南,第三版是最新版。它涵盖了Java编程中一些常见问题和技巧,以及如何编写更加优雅、健壮和高效的Java代码。 该书共分为15章,每一章都涵盖了Java编程中的一个关键…...

CTA进网测试《5G消息 终端测试方法》标准依据:YDT 3958-2021
GB 21288-2022 强制国标要求变化 与GB 21288-2007相比, 新国标主要有以下变化: 1. 增加职业暴露定义: 2. 增加吸收功率密度定义: 3. 增加不同频率、不同人体部位适用的暴露限值: 4. 增加产品说明书的注释:…...
[LeetCode复盘] LCCUP‘23春季赛 20230422
[LeetCode复盘] LCCUP23春季赛 20230422 一、总结二、 1. 补给马车1. 题目描述2. 思路分析3. 代码实现 三、2. 探险营地1. 题目描述2. 思路分析3. 代码实现 四、 3. 最强祝福力场1. 题目描述2. 思路分析3. 代码实现 五、 4. 传送卷轴1. 题目描述2. 思路分析3. 代码实现 六、 5…...

传统燃油车的智控App远控响应速度优化方向几点思考
一、分析当前问题及其影响因素 网络延迟:燃油车的App远控响应速度受到网络延迟的影响。网络延迟可能是由于网络拥堵或服务器响应速度慢等原因导致的。 用户设备:用户设备的性能也会影响燃油车的App远控响应速度。例如,设备的内存不足或存在故…...
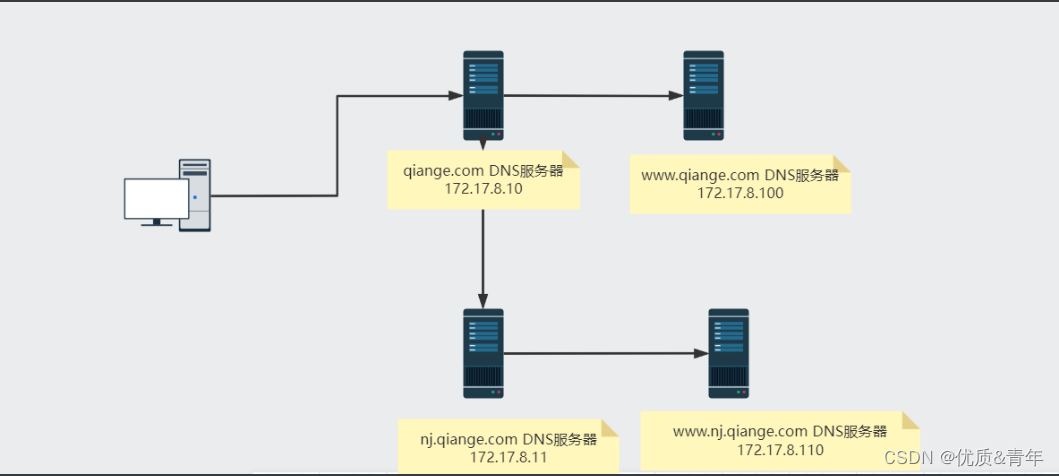
回炉重造九---DNS服务器
1、DNS服务器的相关概念和技术 1.1 DNS服务器的类型 主DNS服务器从DNS服务器缓存DNS服务器(forward DNS服务器{转发器}) 1.1.1 主DNS服务器的作用 管理和维护所负责解析的域内解析库的服务器1.1.2 从DNS服务器的作用 从主服务器或从服务器“复制”解…...
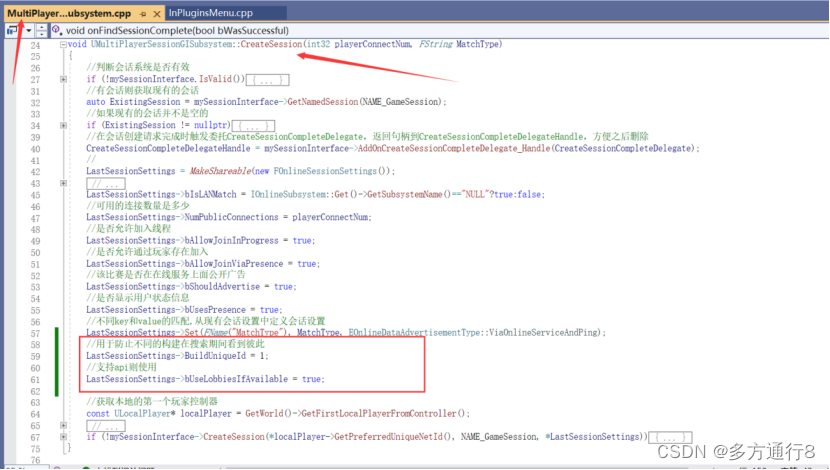
UE4/5多人游戏详解(七、自定义委托,实现寻找会话和加入会话的函数,通过Steam进行两台电脑的联机)
目录 可能出现问题(在六部分的测试可能无法连接的问题【在末尾加上了,怕有人没看见在这里写一下】) 自定义委托 调整位置 创建更多的委托和回调函数给菜单: 多播和动态多播 代码: 委托变量 代码: 回…...
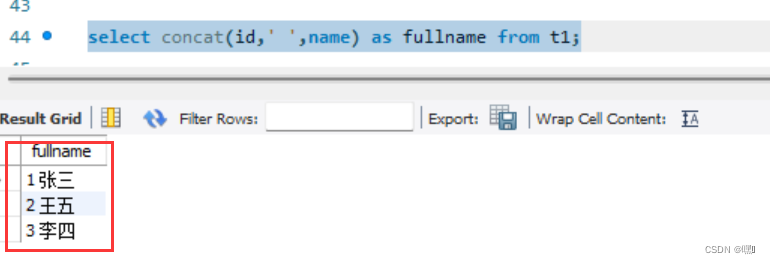
【数据库多表操作】sql语句基础及进阶
常用数据库: 数据库(Database)是按照数据结构来组织、存储和管理数据的仓库,它是长期存储在计算机内、有组织、有结构的数据集合。数据库是信息系统的核心部分,现代软件系统中大量采用了数据库管理系统(DBM…...

DPDK和RDMA的区别
网络的发展好像在各方面都是滞后于计算和存储,时延方面也不例外,网络传输时延高,逐渐成为了数据中心高性能的瓶颈。因为传统两个节点间传输数据的网络路径上有大量的内存拷贝,导致网络传输效率低下,网络数据包的收发处…...

体验 Google Bard
环境 windows 10 64bitGoogle Bardpython 3.8 简介 本篇介绍一个开源的 Google 聊天机器人Bard 的 API 逆向工程,使用它,可以免费的使用 Bard 服务,项目地址:https://github.com/acheong08/Bard 安装及使用 通过 pip 来安装 pip &…...

MITA触摸屏维修WP4053米塔工控机控制屏维修
MITA-TEKNIK米塔触摸屏维修工控机工控屏控制器维修DISPLAY 2COM全系列型号 Mita-Teknik触摸屏维修常见故障:上电无显示,运行报故障,无法与电脑通讯,触摸无反应,触控板破裂,触摸玻璃,上电黑屏&a…...
Nacos简介 安装 配置
简介 什么是注册中心 注册中心在微服务项目中扮演着非常重要的角色,是微服务架构中的纽带,类似于通讯录,它记录了服务和服务地址的映射关系。在分布式架构中,服务会注册到这里,当服务需要调用其它服务时,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
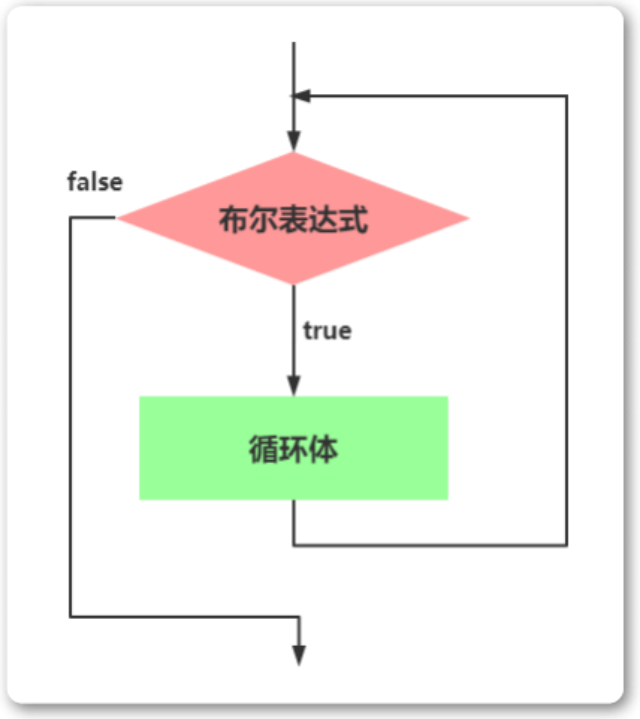
循环语句之while
While语句包括一个循环条件和一段代码块,只要条件为真,就不断 循环执行代码块。 1 2 3 while (条件) { 语句 ; } var i 0; while (i < 100) {console.log(i 当前为: i); i i 1; } 下面的例子是一个无限循环,因…...
