如何在比特币系统内创造人工生命

信息来源:coingeek.com
自2015年以来,关于比特币能否进行复杂计算以及比特币是否“图灵完备”的争论一直在持续。不幸的是,现在存在着一种流传甚广的谬论,有人说比特币并非图灵完备的,它不能像以太坊区块链那样进行复杂的计算。在本文中,我们将对比特币图灵完备性的历史进行考察,然后我们将创造出可在比特币系统内永生的人工生命。
比特币图灵完备性的历史
2015年,Craig S. Wright博士首次被比特币世界所了解,当时他参加了一场圆桌讨论,身份是“前学者”,从事着“无人知晓的商业研究”。他在自我介绍时说他自己是“很久以前”就挖过比特币的人,对于一个当时还不为业内人士所熟知的人来说,这是一段非常神秘的登场介绍。与他一起参加圆桌讨论的嘉宾可以说是星光熠熠,其中有美国铸币局前局长Ed Moy、新自由美元项目创始人Joseph Vaughn Perling、比特币早期投资者Trace Meyer以及Bit Gold创始人Nick Szabo。
对于任何有兴趣回顾比特币发展史的人来说,这是一场不可错过的圆桌讨论。在讨论开始后不久,Wright博士就针对比特币提出了一个令人惊讶的说法,让与会专家都感到困惑不已。他声称,比特币和比特币脚本,即由中本聪创建的编程语言,能够进行复杂的计算,并且是图灵完备的。
计算系统的图灵完备性是指该系统能够解决任何计算层面的问题。用计算机科学中更简单的术语来说,如果一个系统可以“循环”,那么它就是图灵完备的。由于比特币脚本是否能够进行循环并非一眼就能看出来,因此大众普遍认为比特币不是一个图灵完备的系统。为了理解Wright博士当时的大胆主张,我们必须回顾“区块链”和“加密货币”的现代历史。
2013年,Vitalik Buterin发布了题为《以太坊:下一代智能合约和去中心化应用平台》的白皮书,世界首次了解到了以太坊。Buterin提到了以太坊的必要性,因为“在比特币中的脚本语言实施方案面临多项重大限制”,首当其冲的便是“缺乏图灵完备性”。此后不久,在以太坊白皮书中,以太坊被称为“一种内置了图灵完备编程语言的区块链,允许任何人编写智能合约和去中心化应用。”
到2015年展开上述圆桌讨论时,比特币仍被视为功能严重受限的区块链,以太坊则被视为可用于复杂智能合约的区块链。“比特币具有局限性”这种观念导致了“第二代”和“第三代”区块链这类更加荒谬的构想的诞生。这种做法暗示着,虽然比特币是一个很好的起点,但在创造一个可以处理所有交易的全球级区块链的道路上,比特币只是迈出了第一步。
Nick Szabo显然对Craig的说法感到困惑,他立即对Wright博士的说法做出了回应。他表示,Wright所说的东西“略为深奥”了,如果比特币“不是图灵完备的,那么无论它能否处理部分的循环,它也不是像以太坊那样的通用编程语言。”详情请见后附的视频。
圆桌讨论没有再就这一话题进行更深入的交流,我们在接下来的几年里都没听说过比特币有能力进行复杂计算。碰巧的是,我们又一次从Wright博士本人那里听到了这种说法。
到2017年7月,比特币处于大分叉的前夜。有一部分人正确认识到了的比特币规模是被人为限制了,这些人聚集在阿纳姆(Arnhem),召开了“The Future of Bitcoin”大会,就比特币的前进之路进行着讨论。Wright博士原本未被安排在这次会议上发言,但幸运的是,比特币基金会的前董事Jon Matonis放弃了自己的发言时间,选择了让一位他认为是中本聪的人代替他发言。在被认为是比特币的创造者之后,这算得上是Wright博士的首次公开露面。他发表了一场充满激情的演讲,讲述了他对比特币未来几十年的展望。
演讲第26分钟,一张标题为“图灵完备性”的幻灯片弹了出来。他叹了口气说:“关于这个问题,我真是不想再说了。你们猜怎么着?你们都错了,它是(图灵完备的)”。

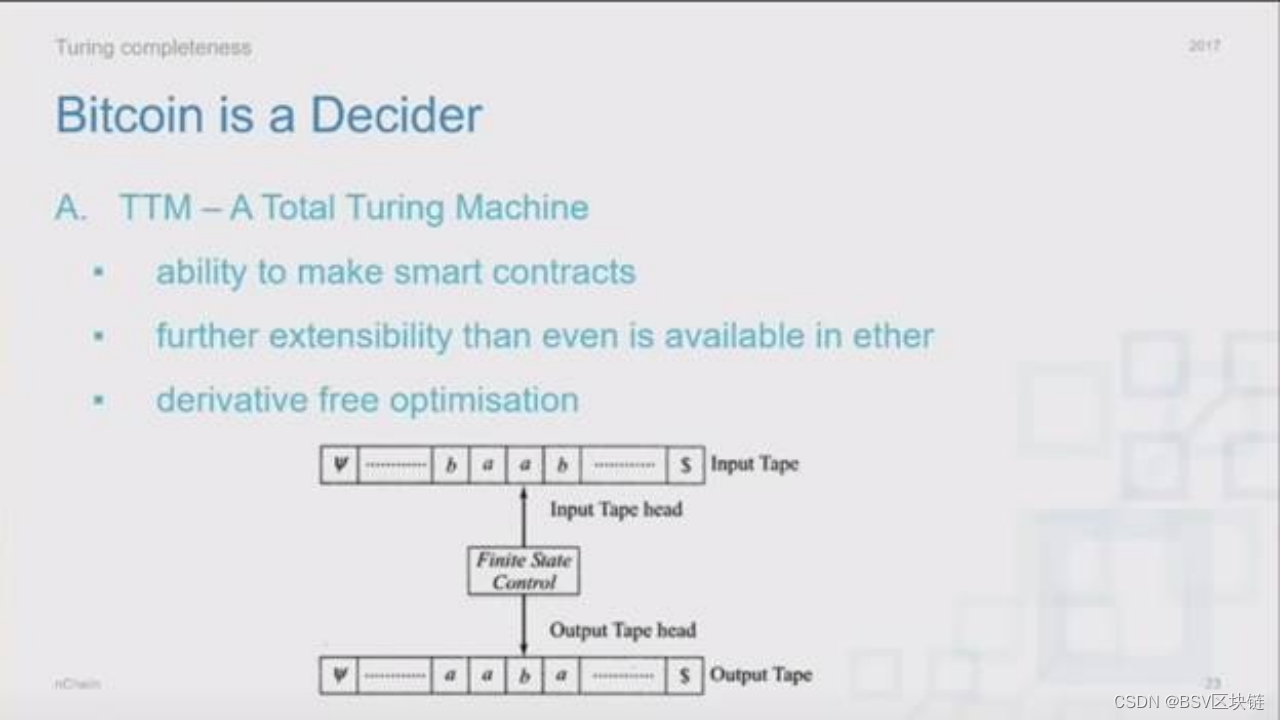
当他在讨论比特币的脚本系统如何构成了一种名为“判定机(decider)”的特殊图灵机的基础时,他翻到了一张幻灯片,上面展示了一个有趣的图案,数学家们马上就能认出这就是Wolfram 110元胞自动机:
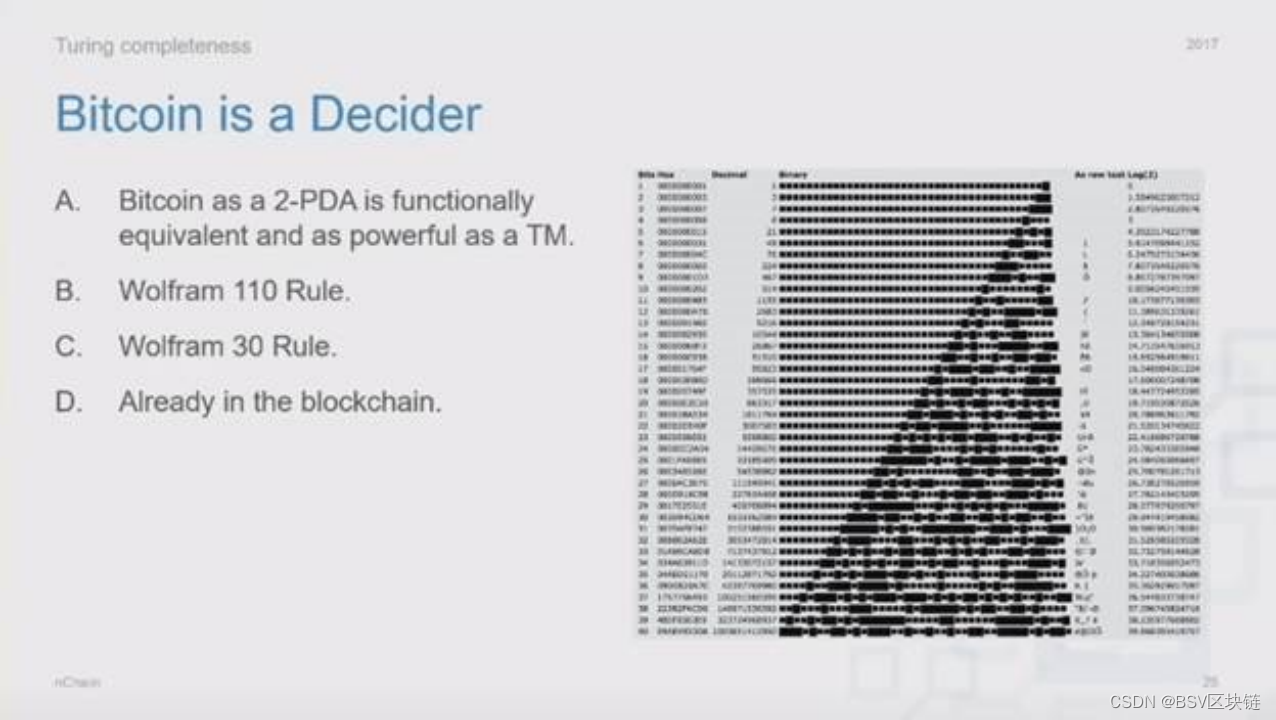
元胞自动机是由Stanislaw Ulam和John Von Nuemann发现的,这是一个引人入胜的研究领域,与数学家Stephen Wolfram的关系最大,他所从事的是一维元胞自动机的系统研究。我鼓励你去了解一下这个迷人的研究领域,但对于元胞自动机,我们有一种简单的思考方式:给定一个初始状态和一个简单的规则集,元胞自动机可以进化出复杂的系统。在20世纪70年代,二维元胞自动机康威《生命游戏(Conway’s Game of Life)》吸引了学术领域之外人士的兴趣,从这时开始,元胞自动机开始普及开来。我们还会再次谈到康威《生命游戏》,但需要注意的是,Wolfram在20世纪80年代开始了元胞自动机的研究,并在这些一维元胞自动机,或者说初级元胞自动机中发现了复杂的行为。
由Wolfram发现的“规则110(Rule 110)”是一种初级元胞自动机,它展现出了非常有趣的行为,并且观察者很难定义这些行为是稳定的还是混沌的。“规则110”已被认为是图灵完备的,这意味着任何计算或计算机程序都可以用这种自动机来模拟。
Wright博士称“规则110”为“最简单的图灵完备系统”,并在阿纳姆的演讲中揭示了一项令人震惊的事实。“这是在比特币上运行的……我们在比特币上运行了粒子群优化(PSO)。”他非常遗憾地表示,当时比特币高昂的手续费扼杀了这个研究项目。“我们在比特币上运行了第一段可自我演化的代码,持续了两年。”他接着说道,随后再次提到BTC链的高昂费用扼杀了这个项目。
这本应该是一条更加劲爆的新闻,因为这个项目证明了,在比特币中,图灵完备计算是可能的。然而,出于某种原因,所谓的区块链行业对这种观点置之不理。在2017年的加密货币热潮中,大众媒体市场反复强调以太坊是“可编程版”的比特币。
2018年3月,Clemens Ley第一个站出来公开支持Wright博士的说法,并在东京中本聪愿景大会上做了题为“为什么比特币是图灵完备”的演讲。Clemens的专业是自动机理论,他独立撰写了一篇与这一论点相关的证明,并给出了证明的相关解释。他在演讲开始时指出,“许多人认为在比特币中不可能实现的事情实际上是可以做到的。”随后他进行了实际的演示,展示了如何将区块链用作图灵完备计算所需的纸带。在撰写本文时,他的演讲仅获得了3479次观看。对于任何怀疑比特币能否实现图灵完备计算的人而言,这段演讲都值得仔细研究。同样是在2017年,Wright博士的说法得到了另一位独立研究者Konstantinos Sgantzos的验证,他发表了一篇论文,题为《在区块链上实现丘奇-图灵-多伊奇原理机器》。
比特币的创造者在试图向世界宣传自己的发明时竟然被视为了异教徒,这真是讽刺。虽然我曾公开对此表示过不解,但我承认,在Wright博士所创造的这个领域中,他确实颇具争议。尽管我个人非常感谢他花了无数时间在公共论坛上向我和其他人传授与比特币本质相关的知识,但很少有人去愿意验证他的说法。虽然我们可以坐等更多学者来验证Wright博士的说法,但也有一些人愿意亲自进行验证。
《生命游戏》
我有幸在2019年旧金山的BSV聚会活动上见到了刘晓晖。我们寒暄了几句,简单地探讨了一下我们希望用比特币来解决的、硅谷公司内在的诸多问题。
我回到家后,收到了晓晖给我发的一条消息,其中是他的sCrypt项目的链接。他说他已经用C++构建了一个功能完整的比特币脚本编译器,就好像这个项目对他来说根本不费吹灰之力一样。晓晖是我在比特币领域中最喜欢的创新者之一,他一直在使用普通的C++语言向其他程序员展示比特币脚本的可能性。
想要验证Wright博士的观点说来也简单,那就是使用比特币脚本来复制一个图灵完备系统,比如说前面提到的规则110或者康威生命游戏。晓晖用C++发布了康威《生命游戏》的代码模板,这让我们的工作轻松了许多。生命游戏是一种在二维网格上进行的元胞自动机。
生命游戏相对来说是比较简单的,由四条规则组成。前三条规则适用于黄色活细胞,最后一条规则适用于灰色死细胞:
1.周围只有一个邻居或没有邻居的活细胞都会死亡,就像是孤独而终一样。
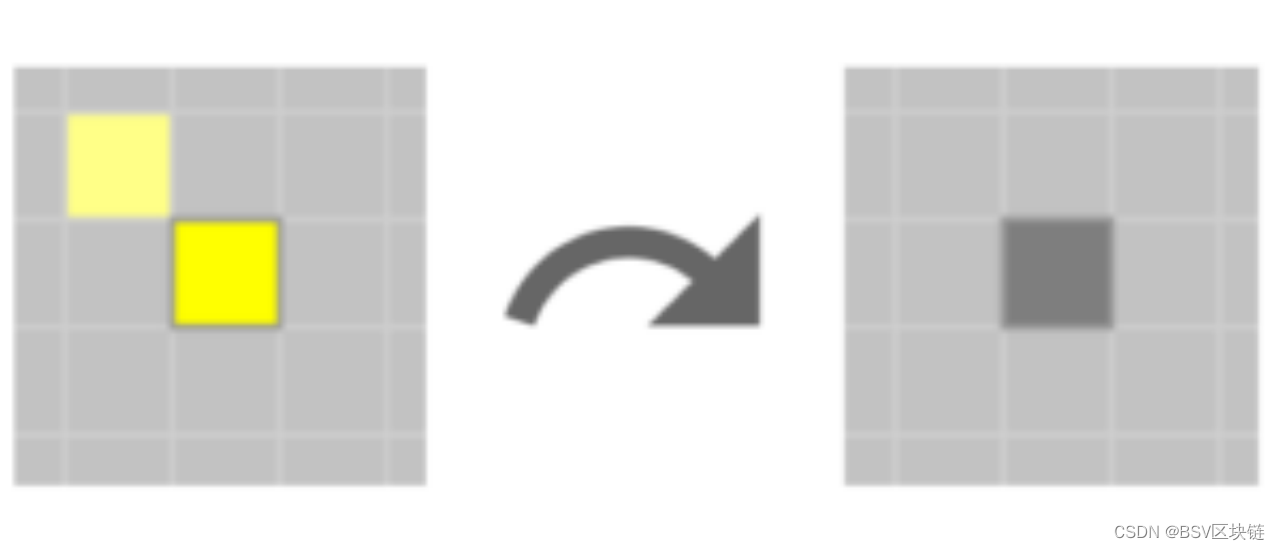
2.周围有四个或更多邻居的活细胞都会死亡,就如同人口过剩一样。

3.周围有两到三个邻居的细胞可以继续存活。

4.周围恰好有三个邻居的死细胞可以复活。

你可以用这个小程序玩一玩《生命游戏》。生命游戏对于学者和普通观察者来说都很有趣,因为只需基于这个简单的规则集进行初始配置,就可以创建出各种复杂的模式和“生命形式”。“积木”、“蜂箱”、“独木舟”等等都是可以在《生命游戏》中存在的静态物体。我们甚至也能看到像“滑翔机枪”一样的动态“生命”的出现。这个元胞自动机中的世界非常奇特,你越深入了解,就会越觉得它越奇特。
通过在区块链上创建一个初始配置,我们就可以观察它的演变方式。由于康威《生命游戏》是图灵完备的,如果我们可以在比特币区块链上复制这款游戏,那么我们就可以切实证明,比特币实际上在所有方面都是图灵完备的。如果你想知道为何比特币上未曾有过这样的项目,你只需快速看一下比特币脚本中的代码,就会恍然大悟了。这是一个体积相当大的脚本,在BTC链上是不可能实现的。因为BSV是唯一一个实现了中本聪原始设计的区块链,这个项目只有在BSV上才有实现的可能。
我们决定对此进行测试。我们能让康威《生命游戏》存在于区块链之上吗?
是的,我们可以!在这里,我们公布了4×4棋盘上康威《生命游戏》的初始配置。我们的起始配置是3个细胞:

看过上述链接中交易脚本的人会发现,我们使用了一个看起来像这样的游戏棋盘:
00000000
00000100
00010100
00000000
你可以查看这个脚本的脚本哈希,了解一下游戏二次迭代的情况。根据《生命游戏》的规则,在这笔交易中,我们最终会得到一种名为方块的“静态物体”:

或者你也只可以使用下面这种棋盘:
00000000
00010100
00010100
00000000
在游戏中迭代5次以上,便可在《生命游戏》中保存所见到的这种稳态静物。我们在区块链上创造了永恒的生命!阻止我们创造更复杂系统的唯一原因是所涉及到的经济因素。中本聪的天才之处在于将经济学纳入了这个系统!只要有资金支持,我们的游戏就能持续进行下去。
我们可以看到,比特币内部是能够运行一个图灵完备的系统的,这证明了比特币本身就是图灵完备的。只要再多做一点工作,我们就可以创建一个互动生命游戏棋盘,玩家可以与之互动,并为其注资以维持其生命活力。
这些有什么意义呢?首先,这完全否定了试图贬低比特币的复杂计算能力的人的观点。在BTC上,他们删除了必需的操作码、限制了交易和脚本的规模以及区块的大小,进而故意削弱了比特币的计算能力。因为BTC支持者的误导性言论,将他们的区块链称为比特币,所以人们普遍认为比特币不能进行复杂的计算。但对于BSV生态中的许多人来说,这并非什么出乎意料的事情,这也证明了Craig Wright博士的正确性。
Wright博士是比特币的创造者,这一点不容否认。他曾多次对比特币的本质做出过令人难以置信的断言,而这些断言后来都被证明是正确的。无论是比特币网络拓扑结构的小世界网络的性质、保护网络安全的经济激励因素,还是系统本身的图灵完备性,Wright博士一再证明,对于自己所发明的技术,他是不折不扣的专家。
一方面,以太坊无法实施任何真正有意义的扩容举措;而在另一方面,BSV却正在快速向TB级、甚至更大体积的区块扩容。比特币具备以太坊的所有功能,但比特币同时还拥有中本聪设想中的大规模可扩容性。
Craig Wright在比特币的图灵完备性问题上的正确性得到了证明,这件事对我们Britevue来说并不奇怪。我们在基于比特币构建未来的线上评论应用时,这个复杂的系统就需要比特币的智能合约和通证化功能,但这两项都是之前被认为在比特币中不可能实现的功能。
我要向刘晓晖表示感谢,感谢他在部署《生命游戏》合约方面提供的帮助,同时也要大力感谢Dylan Murray为比特币注入生命。
目前,全球已有超过400个项目构建于BSV区块链之上。凭借坚如磐石的协议及超高的网络性能,BSV生态系统迅猛发展,我们期待未来出现更多前所未有的商业应用。
- 对BSV区块链开发感兴趣的朋友,可以前往我们的中文开发者专区:BSV区块链
相关文章:

如何在比特币系统内创造人工生命
信息来源:coingeek.com 自2015年以来,关于比特币能否进行复杂计算以及比特币是否“图灵完备”的争论一直在持续。不幸的是,现在存在着一种流传甚广的谬论,有人说比特币并非图灵完备的,它不能像以太坊区块链那样进行复杂…...
除了Figma,再给你介绍10款好用的协同设计软件
组织结构越来越复杂,团队中的每个人都有独特的技能、经验和专业知识。我们怎样才能让团队更好地合作?在这种情况下,协同设计应运而生。 UI的未来是协同设计!如果你想把握未来的设计趋势,不妨从使用高效的协同设计软件…...
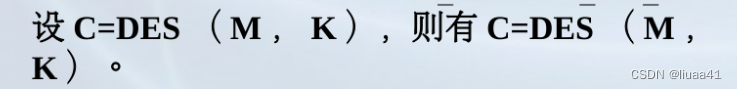
信息安全复习五:数据加密标准(DES)
一、本章梗概 1.主要内容:分组密码、分组密码用到的关键技术和结构、对称密钥密码典型算法DES 2.思考问题: ①按照明文被处理的形式,DES属于标准的分组密码 ②根据密钥的使用数量,DES属于标准的对称密码 3.内容回顾: …...

Java ---包装类
(一)包装类概念 官方说法: Java是面向对象的语言,但是为了便于开发者的使用,Java中却沿用了C语言的基本数据类型,在进行基本的数据计算时,开发者可以直接使用基础类。但是当需要和Java其他对象…...
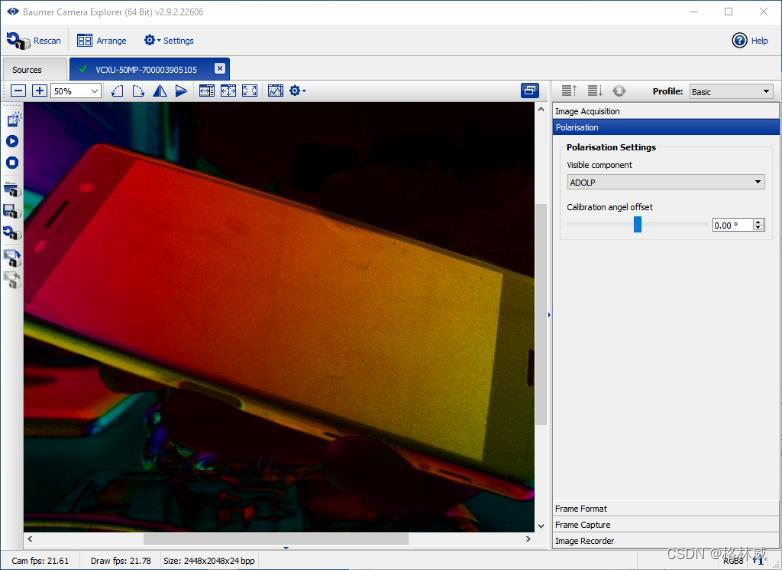
Baumer工业相机中偏振相机如何使用Baumer堡盟GAPI SDK来进行偏振数据的计算转换输出(C#)
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...
 中运行库的链接方式MD和MT的区别)
MSVC(Microsoft Visual C++) 中运行库的链接方式MD和MT的区别
问题描述 MSVC(Microsoft Visual C) 中运行库的链接方式MD和MT的区别 问题解答 在MSVC编译器中,运行库(Runtime Library)有两种链接方式:MD(Multithread-DLL)和MT(Multithread)。这两种链接方式的主要区…...

设计模式之解释器模式(C++)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 一、解释器模式是什么? 解释器模式是一种行为型的软件设计模式,定义了一个解释器,来解释给定语…...

基于MATLAB编程的粒子群算法优化BP神经网络风电功率预测,基于PSO-BP的风电功率预测
目录 摘要 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络的激活函数, BP神经网络的传递函数 粒子群算法的原理及步骤 基于粒子群算法改进优化BP神经网络的风电功率 matlab代码 代写下载链接:https://download.csdn.net/download/a…...

开心档之C++ 字符串
C 字符串 目录 C 字符串 C 风格字符串 实例 实例 C 中的 String 类 实例 C 提供了以下两种类型的字符串表示形式: C 风格字符串C 引入的 string 类类型 C 风格字符串 C 风格的字符串起源于 C 语言,并在 C 中继续得到支持。字符串实际上是使用 …...

Java Collection源码分析(JDk corretto 11)
文章目录 Collection 系列源码分析 (JDK Amazon corretto 11)Collection接口Iterable接口 子接口 QueueQueue的子接口 Deque双端队列 子接口ListArrayList 实现类序列化与反序列化(后续解决)获取Calss对象的方式 主要有三种:Arrays工具类System类 LinkedList实现类t…...
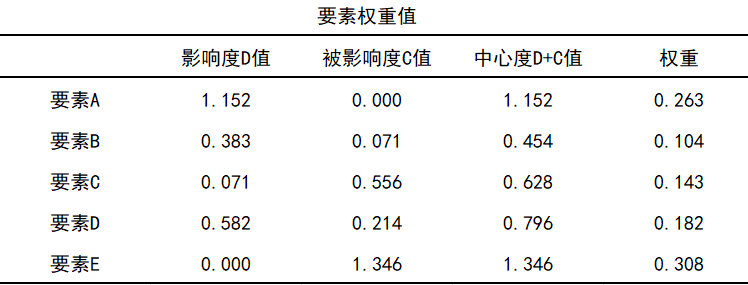
13种权重的计算方法
权重计算方法有很多种,不同的方法有不同的特点和适用情况。AHP层次分析法和熵值法在权重计算中属于比较常用的方法。除此之外,还有一些与权重计算相关的方法,今天一文总结了13种与权重计算相关的方法,大家可以对比选择使用。 一、…...
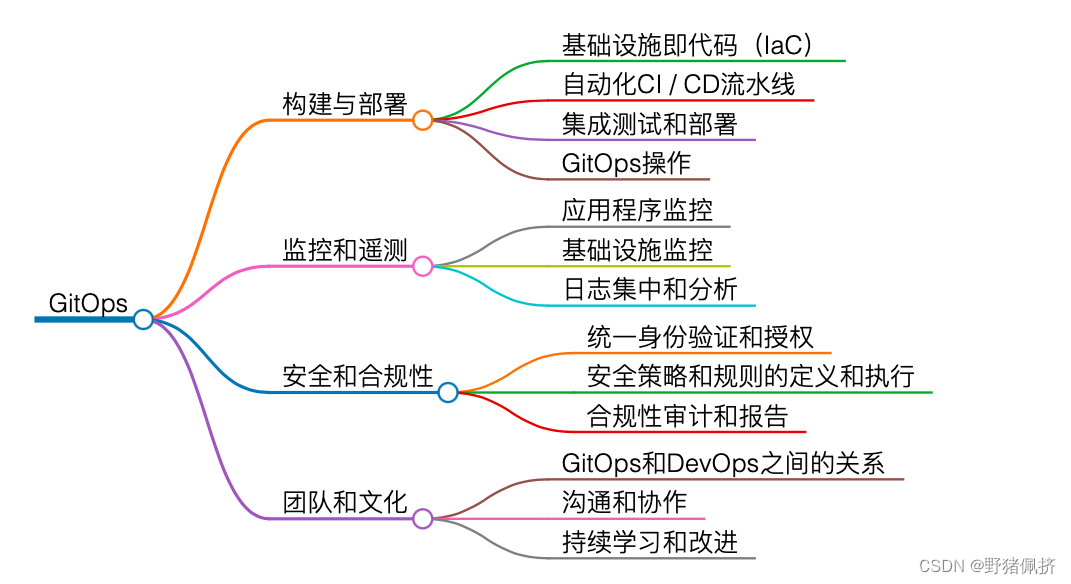
Devops和Gitops区别
一. 什么是devops DevOps 是一种开发(Dev)和运维(Ops)之间协作和沟通的文化、流程和工具的实践方法。它强调迭代、快速交付和持续集成/持续交付,旨在加速软件交付的速度、质量和稳定性。 DevOps 的核心目标是通过自动…...

拿下多家车企定点!4D毫米波雷达「域」系统首发出道
从1R、2R、3R到整车360感知方案,毫米波雷达的前装市场需求量依然保持着快速增长的态势。 高工智能汽车研究院监测数据显示,2022年中国市场(不含进出口)前装标配搭载ADAS毫米波雷达(前向后向盲区)交付1795.…...
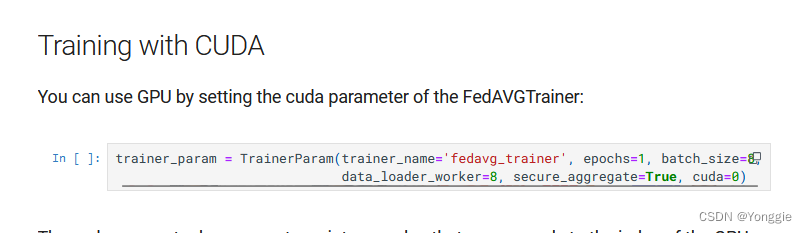
【FATE联邦学习】FATE联邦学习使用GPU、指定cuda下标
问题 FATE框架1.x支持GPU训练吗? 寻找 先看了官网,搜官网,发现还是有的。 打开第一个后,里面可以用training param指定各个client的训练GPU,但是好像都是在large language model的。 而在文档中搜寻到的gpu…...

英文数字表达
1基数词 0 nought;zero;O 1 one 2 two 3 three 4 four 5 five 6 six 7 seven 8 eight 9 nine 10 ten 11 eleven 12 twelve 13 thirteen 14 fourteen 15 fifteen 16 sixteen 17 seventeen 18 eighteen 19 nineteen 20 twenty21 twenty-one 22 twenty-two 23 twenty-three 30 th…...
第11届蓝桥杯省赛真题剖析-2020年6月21日Scratch编程初中级组
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第125讲。 第11届蓝桥杯省赛,这是2020年6月21日举办的省赛Scratch考试真题,原定于2020年3月7日…...
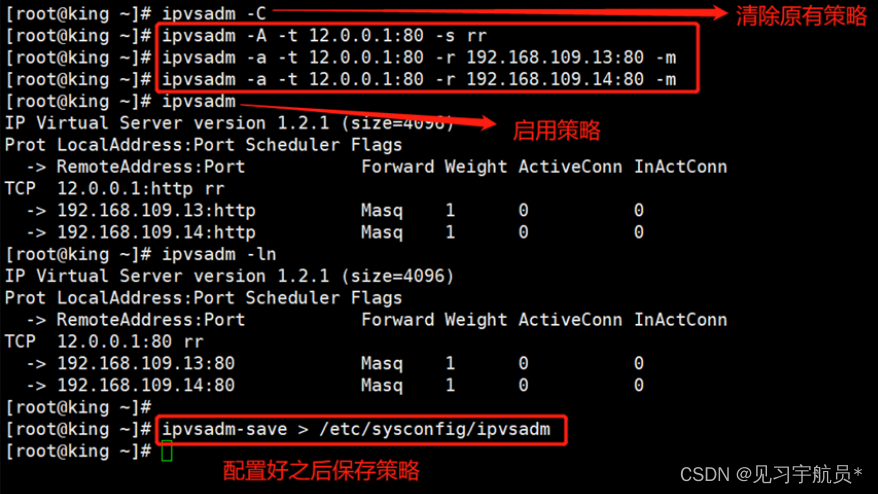
部署LVS-NAT群集实验
一、 实验准备 负载调度器:内网关 ens33:192.168.109.12,外网关 ens37:12.0.0.1外网 Web节点服务器1:192.168.109.13 Web节点服务器2:192.168.109.14 NFS服务器:192.168.109.11 客户端…...

对待工作的九个级别
只要是职场人,每天都要开展本职工作,有的人在职场上混得风生水起、平步青云,有的人却总是在原地踏步踏,总有一种怀才不遇的感叹,为什么呢?其实,差距就在于对待工作的态度上。 今天我们一起与各位…...

第四章 存储结构与管理硬盘
第四章 存储结构与管理硬盘 一、一切从“/”开始 1、Linux系统中常见的目录名称以及相应内容 目录名称应放置文件的内容/boot开机所需文件——内核、开机菜单以及所需配置文件等/dev以文件形式存放任何设备与接口/etc配置文件/home用户主目录/bin存放单用户模式下还可以操作…...

【腾讯云-2】极简搭建边缘集群
1 创建 流程和https://blog.csdn.net/qq_47058489/article/details/130347795差不多,可参考 查看基本信息: 创建边缘集群的过程中会初始化master,说明包含一个托管master节点 但是没有其他节点 2 开启节点远程登录 通过 SSH 的方式远…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
