【最优化方法】1-最优化方法介绍
文章目录
- 1 最优化起源
- 2 最优化发展
- 3 运筹学在国外
- 4 运筹学在国内
- 5 什么是最优化?
- 6 为什么要研究最优化问题?
- 7 最优化问题
- 8 最优化问题分类
- 9 最优化研究内容
- 理论
- 算法
- 应用
1 最优化起源
中国古代优化思想–田忌赛马(公元前340年)
18世纪L.Euler,J.L.Lagrange等对与力学相关的极值问题或者变分问题统一处理方法的研究。
线性规划与单纯形法—George Dantzig 1947,线性规划之父,师从著名统计学家J. Neyman
一个人的潜能是难以预料的,成功的障碍往往来自于心理上的畏难情绪;一定要相信自己,保持积极的态度。
2 最优化发展
Dantzig,Fulkerson和Johnson在1950年研究旅行商问题时提出了线性整数规划问题。
随后,Gomory提出的割平面方法则奠定了现代整数规划算法的基础。
1951年Kuhn和Tucker提出了约束最优化问题必要条件,后称为Karush-Kuhn-Tucker (KKT)条件,标志着现代非线性规划理论研究的开端。
1970年,Victor Klee & George Minty给出实例证明了单纯形方法不是多项式时间的,而是指数级O(2n)O(2^n)O(2n)。
3 运筹学在国外
英国称为 Operational Research,美国称为 Operations Research
起源于二战期间的军事问题,如雷达的设置、运输船队的护航舰队的规模、反潜作战中深水炸弹的深度、飞机出击队型、军事物资的存储等。二战后运筹学应用于经济管理领域(LP、计算机)
1948年英国首先成立运筹学会。
1952年美国成立运筹学会。
1952年,Morse 和 Kimball出版《运筹学方法》。
1959年成立国际运筹学联合会。
4 运筹学在国内
1956年成立运筹学小组。(1955年钱学森回国)
1958年提出运输问题的图上作业法。
1962年提出中国邮路问题。
1964年华罗庚推广统筹方法。
1982年加入国际运筹学联合会,并于1999年8月组织了第15届大会。
5 什么是最优化?
根据国际数学优化学会定义,最优化是指在一定约束条件下极大化或极小化某一目标函数的问题,其变量可能是连续或离散或随机的。
通俗解释,在所有可能中挑选最好的。
6 为什么要研究最优化问题?
最优化问题无处不在。
早在18世纪,著名数学家欧拉就曾说:宇宙万物无不与最小化或最大化的原理有关系。
可以说,最优化的原理渗入到社会发展的各个方面,甚至在我们的日常生活里也有各种各样的最优化问题。
经济金融: 最大利润、最小风险。
交通运输: 列车运行图、物流。
信息科学: 数据挖掘、图像处理。
生命科学: DNA 序列、蛋白质折叠。
工程力学: 最大载重、结构最优。
军事国防: 摆兵布阵、后勤保障。
7 最优化问题
向量优化
互补与均衡问题
组合优化
随机优化
半定规划
鲁棒优化
稀疏优化
统计优化
张量与多项式优化
非光滑优化
8 最优化问题分类
CONSTRAINED AND UNCONSTRAINED OPTIMIZATION
GLOBAL AND LOCAL OPTIMIZATION
STOCHASTIC AND DETERMINISTIC OPTIMIZATION
CONTINUOUS VERSUS DISCRETE OPTIMIZATION
9 最优化研究内容
理论
线性规划
非线性规划
一阶/二阶最优性条件
对偶理论
鞍点问题
灵敏度分析
复杂性分析
算法
最速下降方法
共轭梯度方法
牛顿方法
拟牛顿方法
投影方法
罚函数方法
应用
建立模型
理论分析
编程计算
解决实际问题
相关文章:

【最优化方法】1-最优化方法介绍
文章目录1 最优化起源2 最优化发展3 运筹学在国外4 运筹学在国内5 什么是最优化?6 为什么要研究最优化问题?7 最优化问题8 最优化问题分类9 最优化研究内容理论算法应用1 最优化起源 中国古代优化思想–田忌赛马(公元前340年) 18世纪L.Euler࿰…...

数据结构 | 树 | 二叉树
🔥Go for it!🔥 📝个人主页:按键难防 📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀 📖系列专栏:数据结构与算法 ὒ…...

笔记:使用 unbuild 搭建 JavaScript 构建系统笔记
使用 unbuild 搭建 JavaScript 构建系统jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 简介: 本文是笔者阅读分析 elementPlus 项目时记录的。该项目用到了一个完全没有文档和资料的工具 unbu…...
【SpringBoot3.0源码】启动流程源码解析 •下
文章目录初始化DefaultBootstrapContext开启Headless模式获取监听器并启动封装命令行参数准备环境打印Banner创建上下文容器预初始化上下文容器刷新Spring容器打印启动时间发布事件执行特定的run方法上一篇《【SpringBoot3.0源码】启动流程源码解析 • 上》,主要讲解…...
QT(56)-动态链接库-windows-导出变量-导出类
1.导出变量 1.1不使用_declspec(dllimport) _declspec(dllexport) 使用_declspec(dllimport) _declspec(dllexport) 1.2win32 mydllwin32 myexe 1.3win32 mydllqt myexe 2.导出类 使用_declspec(dllimport) _declspec(dllexport) 2.1不用关键…...
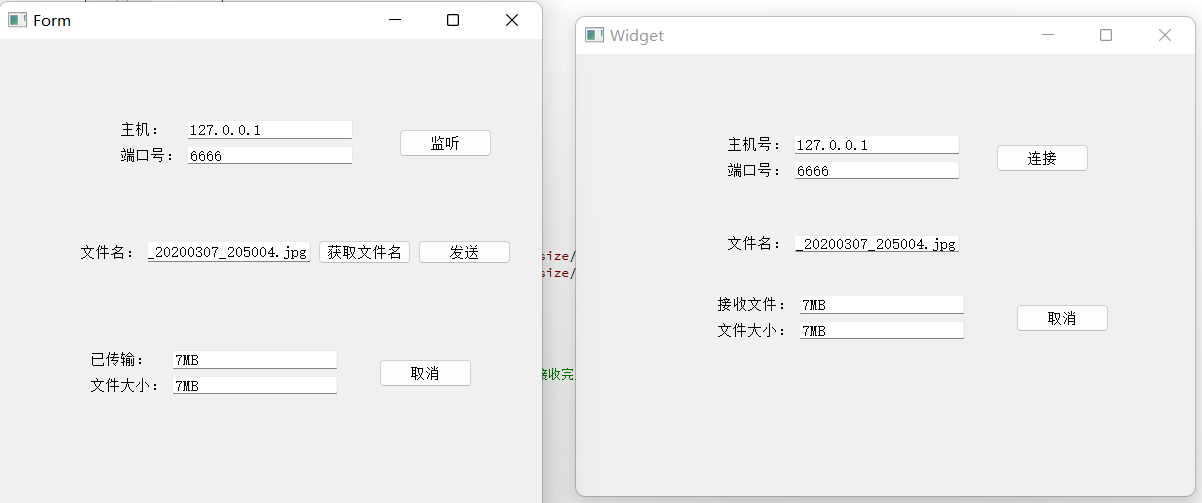
TCP传输文件
传输文件和传输信息的区别: 传输信息,只是一条数据,传输文件是多条数据传输信息传输过去一般都会显示,传输文件一般不会显示,一般只是存放在文件中传输文件需要传输,文件大小和文件名称(不然不知…...
vue3:加载本地图片等静态资源
背景 在我们用 vue2 webpack 的时候,加载图片资源是这样用的: <img :src"require(/assets/test.png)" />这样打包后就会触发 file-loader 打包图片资源,在 dist 文件夹中就可以看到这个图片(如果图片较小会打包…...

工作记录------数据库group_concat函数长度问题
工作记录------group_concat函数长度问题 背景:页面在数据展示时,报错,错误显示:String index out of range: -1 异常信息 java.lang.StringIndexOutOfBoundsException: String index out of range: -1at java.lang.String.sub…...
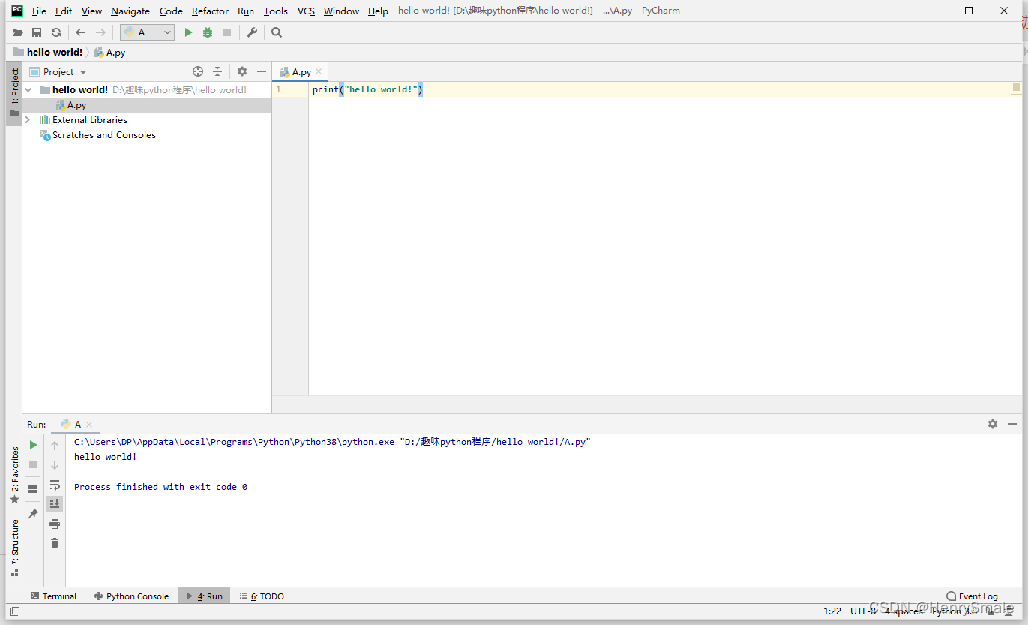
Python基础语法
1 编程环境 1.1 编译环境 pycharmpython/anaconda 1.2 环境设置 File -> settings -> Project interpreter -> 1.3 Hello world 2 条件判断 2.1 例题 【题1】输入一个年份,判断是否是闰年 ①能被4整除,但不能被100整除; ②能被400整…...
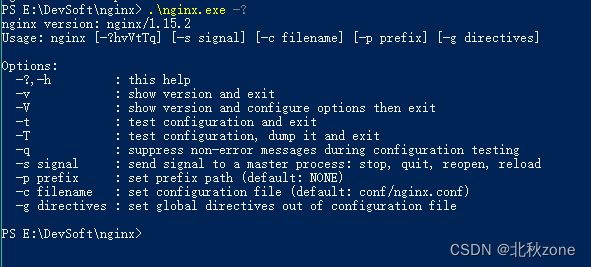
windows环境下安装Nginx及常用操作命令
windows环境下安装Nginx及常用操作命令nginx基本概述基本用途nginx安装nginx基本概述 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器。基本用途 nginx是一个轻量级高并发服务器,而tomcat并不是。nginx一般被用来做反向代理,将请求转发到应用…...

python excel数据处理?
前段时间做了个小项目,帮个海洋系的教授做了个数据处理的软件。基本的功能很简单,就是对Excel里面的一些数据进行过滤,统计,对多个表的内容进行合并等。之前没有处理Excel数据的经验,甚至于自己都很少用到Excel。记得《…...
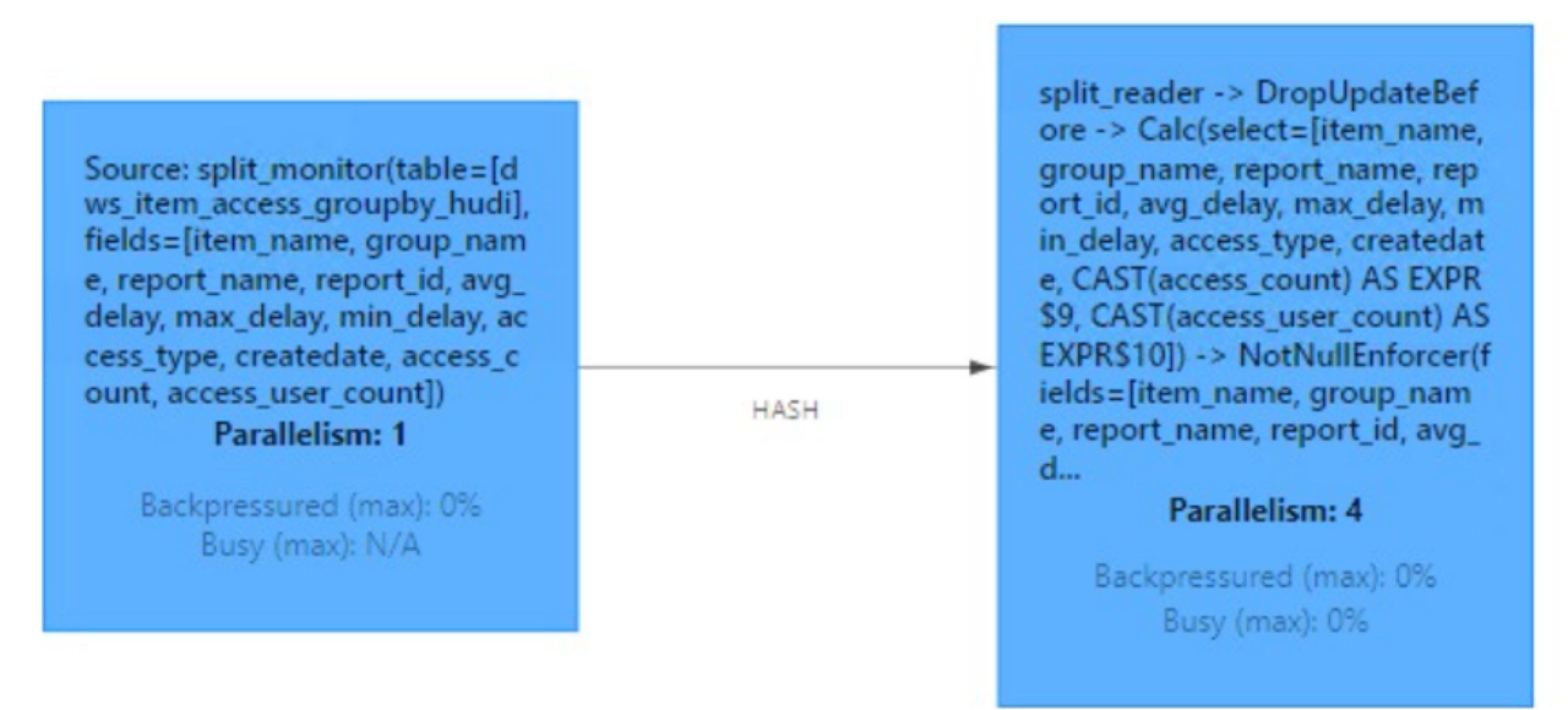
Hudi-集成Flink
文章目录集成Flink环境准备sql-client方式启动sql-client插入数据查询数据更新数据流式插入code 方式环境准备代码类型映射核心参数设置去重参数并发参数压缩参数文件大小Hadoop参数内存优化读取方式流读(Streaming Query)增量读取(Increment…...
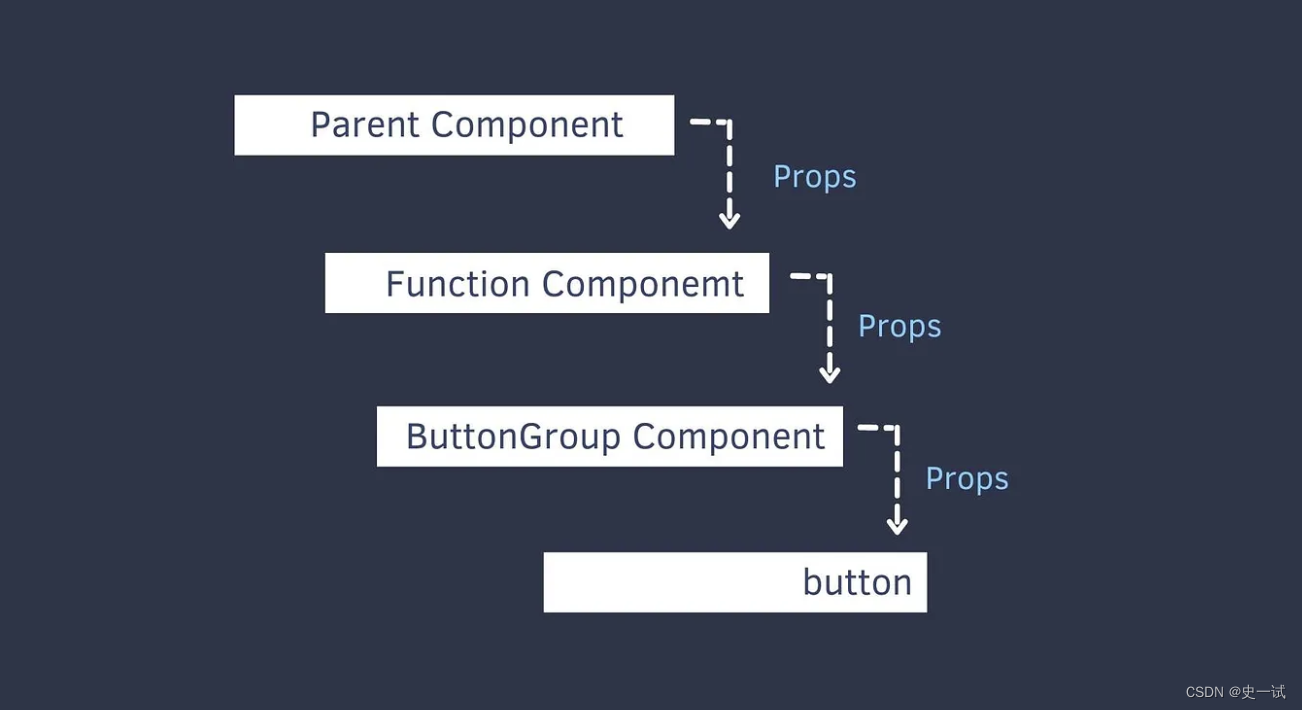
重新认识 React Hooks useContext
通常来说,React 数据的传递方式都是一层一层把资料 props 传到子层的 就算第二层(Function Component)、第三层(Button Group Compontn) 根本没有用到这个资料,但是为了传到最底层(button) ,每一层还是必须要传props // App.js const App = () => {const [dark, setDark…...
数据库(2)--加深对统计查询的理解,熟练使用聚合函数
一、内容要求 利用sql建立学生信息数据库,并定义以下基本表: 学生(学号,年龄,性别,系号) 课程(课号,课名,学分,学时) 选课࿰…...
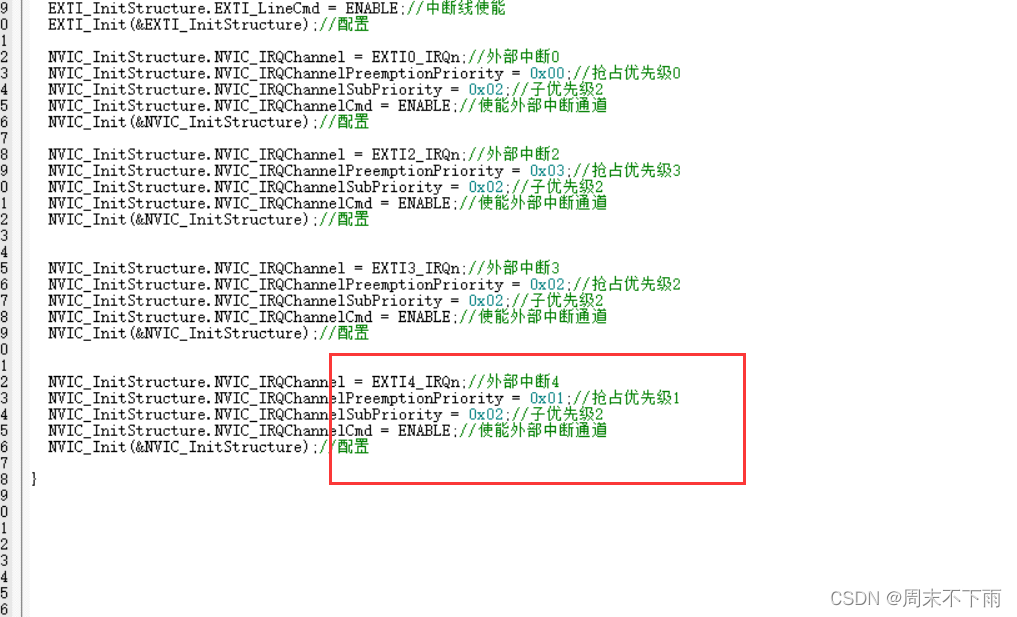
stm32f407探索者开发板(十五)——NVIC中断优先级管理
文章目录零、前言一、NVIC中断优先级分组1.1 中断的管理方法1.2 抢占优先级&相应优先级的区别1.3 举例1.4 特别说明1.5 中断优先级分组函数二、NVIC中断优先级设置2.1 中断设置相关寄存器2.2 中断设置优先级2.2.1 中断优先级控制的寄存器组 IP[240]2.2.2 中断使能寄存器组 …...
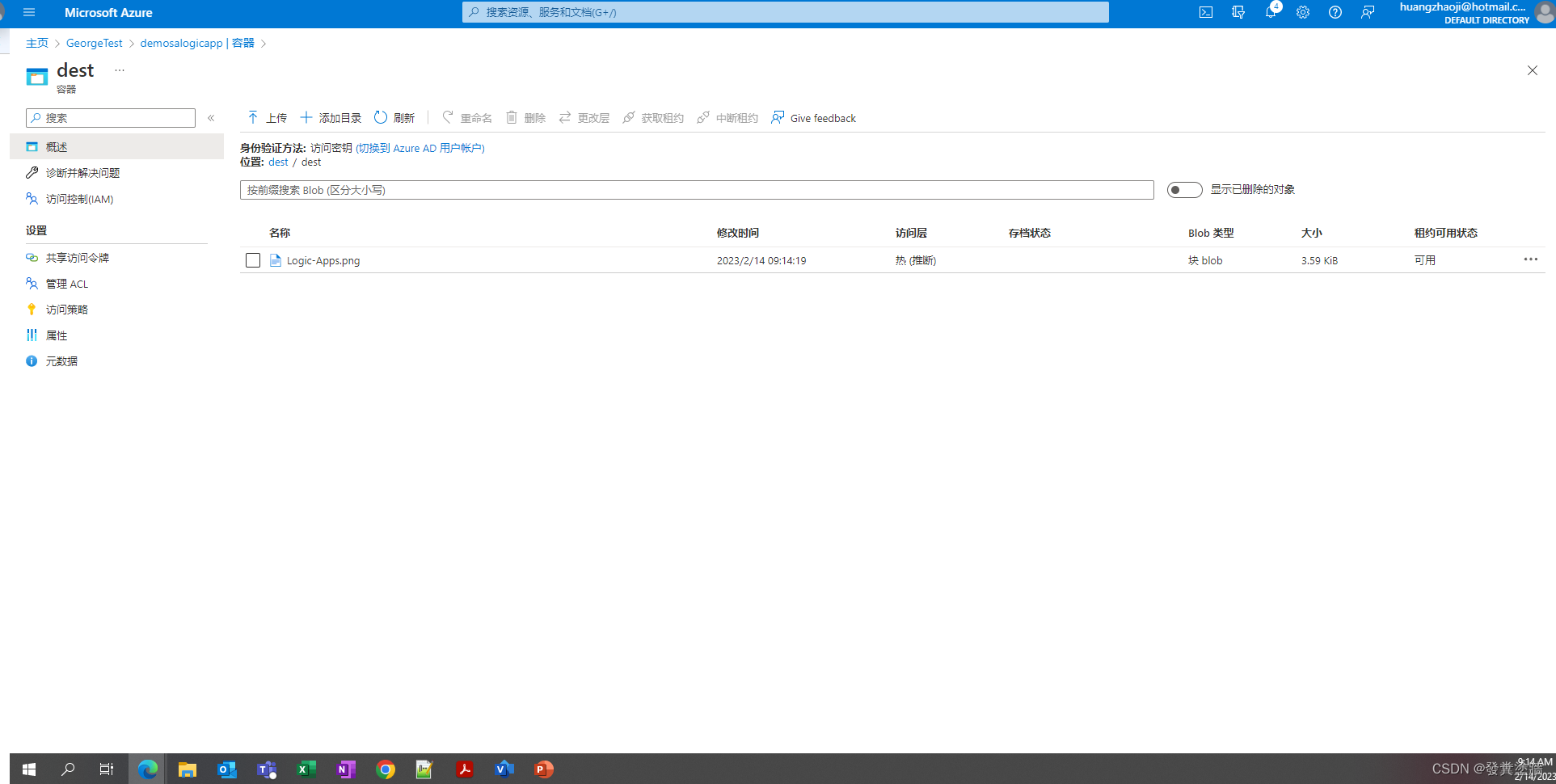
【Azure 架构师学习笔记】-Azure Logic Apps(6)- Logic Apps调用ADF
本文属于【Azure 架构师学习笔记】系列。 本文属于【Azure Logic Apps】系列。 接上文【Azure 架构师学习笔记】-Azure Logic Apps(5)- 标准和使用量类型的区别 前言 Logic Apps 和 ADF 的搭配使用是常见的组合,它们可以互相弥补各自的不足和…...

python随机获取列表中某一元素
1、利用Python中的random模块中的choice方法 random.choice()可以从任何序列,比如list列表中,选取一个随机的元素返回,可以用于字符串、列表、元组等。 import random arr[1,2,3,4,5,6] print(random.choice(arr))2、利用Python中的random模…...

Nacos微服务笔记
Nacos安装Nacos 的 Github(Tags alibaba/nacos GitHub)下载我们所需的 Nacos 版本,可以选择 windows 或者 Linux。 进入官网,选择合适版本,tar.gz为linux版本,zip为windows版本。下载并解压 nacos-server…...
MAC文件误删怎么办?mac数据恢复,亲测很好用的方法
电脑文件误删,应该很多人都经历过。之前分享了很多关于Windows电脑文件误删如何恢复的方法,那么MAC电脑文件误删该怎么办?有什么好方法可以使得mac数据恢复回来吗?下面就给大家分享一些亲测好用的方法! 一、MAC电脑的文…...

机械革命z2黑苹果改造计划第二番-MacOS实用软件渗透工具
机械革命z2黑苹果改造计划第二番-实用软件 Mac实用工具 这是旧电脑改造计划的第二篇,就是安装一些常用软件和一些渗透测试工具,武装灵魂成为真正的生产力工具 首先推荐一个网站,www.mactools.app,这个软件里边有大多数常用的软…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
