【别再困扰于LeetCode接雨水问题了 | 从暴力法=>动态规划=>单调栈】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |

🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ 暴力法
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 动态规划
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 单调栈
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 🍋 总结
- 💬 共勉
🚩 题目链接
- 42. 接雨水
⛲ 题目描述
给定 n 个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
🌟 求解思路&实现代码&运行结果
⚡ 暴力法
🥦 求解思路
暴力法的思路很简单,对于每一个柱子,我们找到其左右两侧的最大高度,分别记为 l e f t M a x leftMax leftMax 和 r i g h t M a x rightMax rightMax,然后计算其储水量 m i n ( l e f t M a x , r i g h t M a x ) − h e i g h t i min(leftMax, rightMax) - height_i min(leftMax,rightMax)−heighti,将所有储水量累加起来即可。
🥦 实现代码
class Solution {public int trap(int[] height) {int n = height.length;int ans = 0;for (int i = 0; i < n; i++) {int leftMax = 0;int rightMax = 0;for (int j = i; j >= 0; j--) leftMax = Math.max(leftMax, height[j]);for (int j = i; j < n; j++) rightMax = Math.max(rightMax, height[j]);ans += Math.min(leftMax, rightMax) - height[i];}return ans;}
}
🥦 运行结果
时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
⚡ 动态规划
🥦 求解思路
我们可以使用动态规划来优化暴力法。首先预处理出每个位置左侧的最大高度和右侧的最大高度,分别存储在数组 l e f t M a x leftMax leftMax 和 r i g h t M a x rightMax rightMax 中。然后对于每个位置,计算其储水量 m i n ( l e f t M a x [ i ] , r i g h t M a x [ i ] ) − h e i g h t [ i ] min(leftMax[i], rightMax[i]) - height[i] min(leftMax[i],rightMax[i])−height[i],将所有储水量累加起来即可。
🥦 实现代码
class Solution {public int trap(int[] height) {int n=height.length;int[] leftMax=new int[n];int[] rightMax=new int[n];leftMax[0]=height[0];rightMax[n-1]=height[n-1];for(int i=1;i<n;i++) leftMax[i]=Math.max(leftMax[i-1],height[i]);for(int i=n-2;i>=0;i--) rightMax[i]=Math.max(rightMax[i+1],height[i]);int ans=0;for(int i=0;i<n;i++) ans+=Math.min(leftMax[i],rightMax[i])-height[i];return ans;}
}
🥦 运行结果
时间复杂度为 O ( n ) O(n) O(n)。

⚡ 单调栈
🥦 求解思路
使用单调栈来优化动态规划。我们使用栈来维护一个递减的柱子高度序列。具体地,遍历到第 i i i 个柱子时,如果当前柱子的高度 h e i g h t [ i ] height[i] height[i] 小于栈顶柱子的高度,则将当前柱子入栈;否则,不断从栈中弹出元素,直到栈为空或者当前栈顶元素的高度大于 h e i g h t [ i ] height[i] height[i],然后将当前柱子入栈。弹出元素时,我们可以计算其储水量,并将其累加到答案中。
🥦 实现代码
class Solution {public int trap(int[] height) {int n = height.length;Stack<Integer> stack = new Stack<>();int ans = 0;for (int i = 0; i < n; i++) {while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int top = stack.pop();if (stack.isEmpty()) {break;}int left = stack.peek();int width = i - left - 1;int heightDiff = Math.min(height[left], height[i]) - height[top];ans += width * heightDiff;}stack.push(i);}return ans;}
}
🥦 运行结果
时间复杂度为 O ( n ) O(n) O(n)。
🍋 总结
本文介绍了三种解法来解决 LeetCode 42 题,即接雨水问题。暴力法时间复杂度较高,使用动态规划和单调栈可以优化其效率。动态规划和单调栈的时间复杂度均为 O ( n ) O(n) O(n)。在实际应用中,可以根据具体情况来选择最合适的方法。
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【别再困扰于LeetCode接雨水问题了 | 从暴力法=>动态规划=>单调栈】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
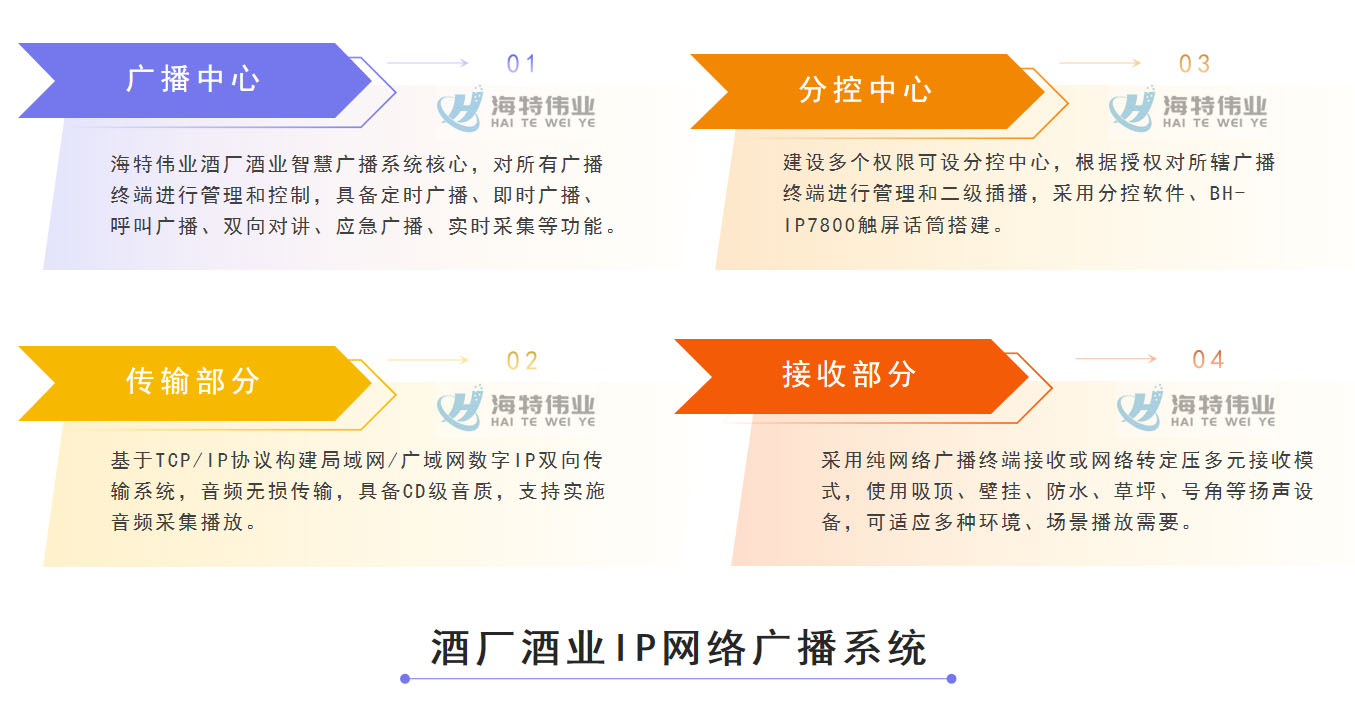
酒厂酒业IP网络广播系统建设方案-基于局域网的新一代交互智慧酒厂酒业IP广播设计指南
酒厂酒业IP网络广播系统建设方案-基于局域网的新一代交互智酒业酒厂IP广播系统设计指南 由北京海特伟业任洪卓发布于2023年4月25日 一、酒厂酒业IP网络广播系统建设需求 随着中国经济的快速稳步发展,中国白酒行业也迎来了黄金时期,产品规模、销售业绩等…...

OpenHarmony JS Demo开发讲解
项目结构 打开entry→src→main→js,工程的开发目录如图所示 其中, i18n文件夹:用于存放配置不同语言场景的资源,比如应用文本词条,图片路径等资源。en-US.json文件定义了在英文模式下页面显示的变量内容,…...
CentOS系统安装Intel E810 25G网卡驱动
因特尔网卡驱动给的都是二进制包,需要编译环境。 首先去Intel下载最新的驱动 E810驱动下载:https://www.intel.com/content/www/us/en/download/19630/intel-network-adapter-driver-for-e810-series-devices-under-linux.html?wapkwe810 里面有三个驱…...

Java经典的String面试题
Java经典的Spring面试题 String是基本数据类型吗? String你是基本数据类型String是可变的话? String是final类型的,不可变怎么比较两个字符串的值一样,怎么比较两个字符串是否同一对象? 比较字符串的值是否相同用equa…...

c# 结构体与类区别
在 C# 中,结构体(struct)和类(class)都是用户自定义类型,它们具有一些共同的特性,比如可以定义字段、属性、方法等。但它们也有一些区别。 下面是一些结构体和类的区别: 定义方式不…...

使用 patch 命令打补丁
之前的这篇文章 git 导出差异 diff 文件 写了导出 diff 、patch 文件。 拿到 patch 文件,用 patch 命令可以快速的把修改内容合入,合入后在 git 上是已修改的状态,如需提交还要 add 、commit 。 patch 语法 patch --help 可以看到 Usage:…...

C++——类和对象[上]
目录 1.初识面向对象 2.类的引入 3.类的定义 4.成员变量的命名规则 5.类的实例化 6.类对象模型 7.this指针 1.初识面向对象 C语言是一门面向过程的语言,它关注的是完成任务所需要的过程;C是一门面向对象的语言,将一个任务分为多个对…...
MySQL日志
目录 一 关于mysql的设计和运行逻辑 二 MySQL的三类日志 三 对于日志的利用 插入查询 1 备份 2 删除重复数据 一 关于mysql的设计和运行逻辑 mysql在启动的时候非常占空间,需要申请很大的空间,但是有时候内存并没有那么多,所以OS会把my…...

TinyURL 的加密与解密、猜数字游戏、 Fizz Buzz、相对名次----2023/4/28
TinyURL 的加密与解密----2023/4/28 TinyURL 是一种 URL 简化服务, 比如:当你输入一个 URL https://leetcode.com/problems/design-tinyurl 时,它将返回一个简化的URL http://tinyurl.com/4e9iAk 。请你设计一个类来加密与解密 TinyURL 。 加…...
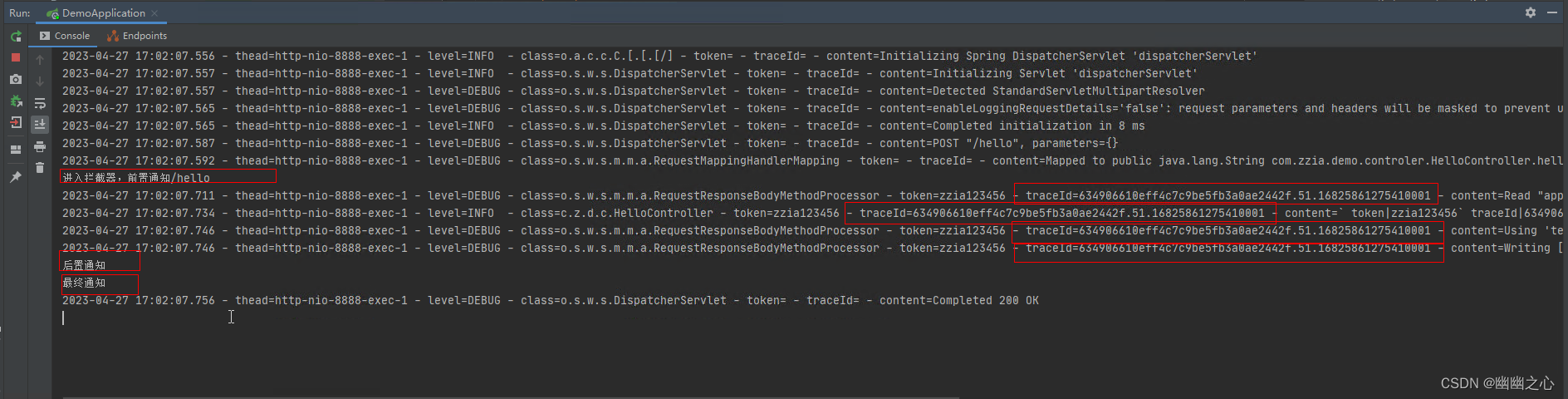
Spring boot结合SkyWalking-Trace工具类实现日志打印请求链路traceid
背景: 随着业务的复杂化、解耦化,运维人员和开发人员需要对请求链路跟踪来快速发现和定位问题,基于应用已经集成了SkyWalking的前提下,如何通过获取SkyWalking生成的统一traceId并加入打印日志中,方便开发人员能够根据…...

精通ES=ElasticSearch
Elasticsearch 是一个分布式、高扩展、高实时的搜索与 数据分析引擎。它能很方便的使大量数据具有搜索、分析和探索的能力。充分利用Elasticsearch的水平 伸缩性,能使数据在 生产环境变得更有价值。Elasticsearch 的实现原理主要分为以下几个步骤,首先用…...
)
RabbitMQ-扇形交换机(Fanout )
扇形交换机:Fanout Exchange扇形交换机是最基本的交换机类型,它所能做的事情非常简单———广播消息。扇形交换机会把能接收到的消息全部发送给绑定在自己身上的队列。因为广播不需要“思考”,所以扇形交换机处理消息的速度也是所有的交换机类…...

Python 学习曲线 从 Python 新手到 Pro
Python 学习曲线 从 Python新手到 Pro 使用代码片段介绍: Python 是世界上最通用和使用最广泛的编程语言之一,以其简单性、可读性和多功能性而闻名。 在本文中,我们将探讨一系列示例场景,其中代码由具有三个不同专业知识水平的程序…...

薪资18K需要什么水平?来看看98年测试工程师的面试全过程…
我的情况 大概介绍一下个人情况,男,本科,三年多测试工作经验,懂python,会写脚本,会selenium,会性能,然而到今天都没有收到一份offer!从年后就开始准备简历,年…...

基于趋动云的 Stable Diffusion Webui 环境搭建
Stable Diffusion Webui 环境搭建,首先新建一个项目: 然后,选择镜像。注意点公开的,已近做好的这个镜像,superx创建,集成了miniconda3的镜像。 然后选择添加数据源,一样,还是点公开&…...

备忘录设计模式解读
目录 问题引进 游戏角色状态恢复问题 传统方案解决游戏角色恢复 传统的方式的问题分析 备忘录模式基本介绍 基本介绍 备忘录模式的原理类图 对原理类图的说明 游戏角色恢复状态实例 应用实例要求 思路分析和图解(类图) 代码实战 备忘录模式的注意事项和细节 问题引…...

股票期货模拟交易有用吗?股票期货模拟交易心得
股票期货市场为了满足新用户的需求,有专门的股票期货模拟交易平台,大家可以在这个平台上进行股票期货的模拟交易,这样可以通过不断总结,丰富我们的知识。下面整理的股票期货模拟交易实验心得,从股票期货模拟交易与实盘…...
2023年五月份图形化三级打卡试题
活动时间 从2023年5月1日至5月21日,每天一道编程题。 本次打卡的规则如下: 小朋友每天利用10~15分钟做一道编程题,遇到问题就来群内讨论,我来给大家答疑。 小朋友做完题目后,截图到朋友圈打卡并把打卡的截图发到活动群…...
100%通过率 详细代码注释)
【华为OD机试真题】字母组合(javapython)100%通过率 详细代码注释
字母组合 知识点回溯 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 每个数字对应多个字母,对应关系如下: 0: a,b,c 1: d,e,f 2: g,hi 3: j,k,l 4: m,n,o 5: p,q,r 6: s,t 7:u,v 8: w,x 9: y,z 输入一串数字后,通过数字和字母的对应关系可以得到多个字母字符串 (要…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
