【算法学习】—n皇后问题(回溯法)
【算法学习】—n皇后问题(回溯法)
1. 什么是回溯法?
相信"迷宫"是许多人儿时的回忆,大家小时候一定都玩过迷宫游戏。我们从不用别人教,都知道走迷宫的策略是:
当遇到一个岔路口,会有以下两种情况:
存在没走过的路。此时可以任意选一条没走过的路深入,只要记住我们所走过的路径即可。
倘若下次再来到这个路口,便不再沿着走过的路径继续深入,而是沿着没走过的路径深入下去;
所有路都已经走过。如果所有岔路口都已经遍历,则回退至上一个最近的岔路口。
当遇到死胡同,便回退到刚才距离最近的岔路口。
不断前进并重复该过程,直到找到终点或回退到起点位置。
其实,这就是回溯法:一个基于深度优先搜索和约束函数的问题求解方法。
(1)、n皇后问题

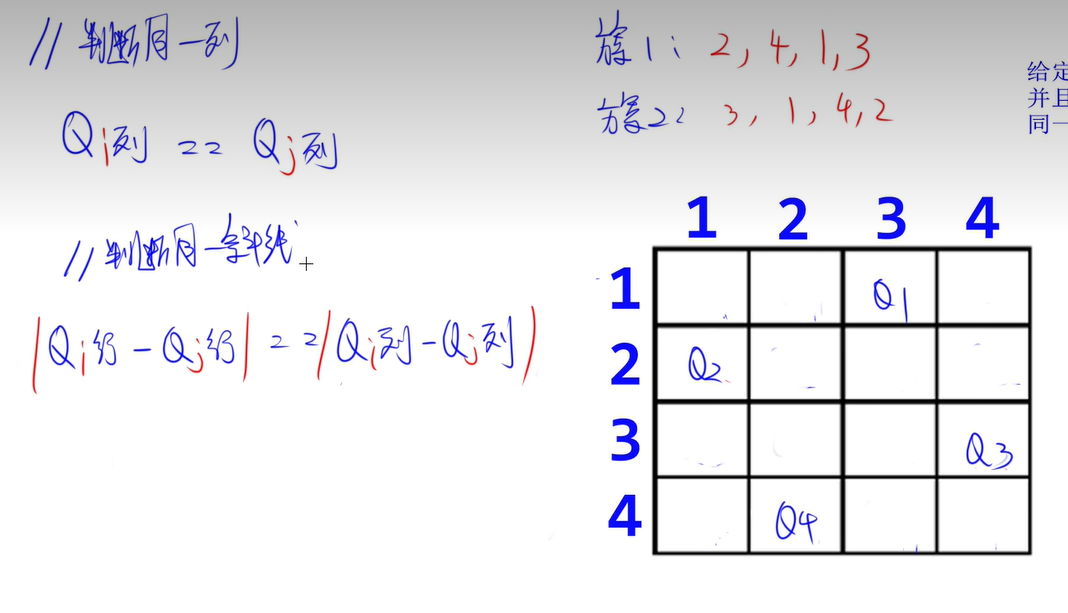
📢 非递归求解n皇后问题
#include <math.h>
#include <stdio.h>
#include <stdlib.h>#define N 4int q[N + 1]; // 存储皇后的列号int check(int j)
{ // 检查第i个皇后的位置是否合法int i;for (i = 1; i < j; i++){if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])){ // 判断是否在同一斜线上return 0;}}return 1;
}void queen()
{ //int i;for (i = 1; i <= N; i++){q[i] = 0;}int answer = 0; // 方案数int j = 1; // 表示正在摆放第j个皇后while (j >= 1){q[j] = q[j] + 1; // 让第j个皇后向后一列摆放while (q[j] <= N && !check(j)){ // 判断第j个皇后的位置是否合法q[j] = q[j] + 1; // 不合法就往后一个位置摆放}if (q[j] <= N){ // 表示第j个皇后的找到一个合法的位置if (j == N){ // 找到了一组皇后的解answer = answer + 1;printf("放案%d:", answer);for (i = 1; i <= N; i++){printf("%d", q[i]);}printf("\n");}else{ // 继续摆放下一个皇后j = j + 1;}}else{ // 表示第j个皇后找不到一个合法的位置q[j] = 0; // 还原第j个皇后的位置j = j - 1; // 回溯}}
}
int main()
{queen();return 0;
}
📢 递归求解n皇后问题
#include <math.h>
#include <stdio.h>
#include <stdlib.h>#define N 4int answer=0;int q[N + 1]; // 存储皇后的列号int check(int j)
{ // 检查第i个皇后的位置是否合法int i;for (i = 1; i < j; i++){if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])){ // 判断是否在同一斜线上return 0;}}return 1;
}void queen(int j){int i;for(i=1;i<=N;i++){q[j]=i;
if(check(j)){// 当摆放的皇后位置为合法时if(j==N){//找到了N皇后的一组解answer=answer+1;printf("方案%d:",answer);for(i=1;i<=N;i++){printf("%d",q[i]);}printf("\n");}else{queen(j+1);//递归摆放下一个位置}
}}
}int main()
{queen(1);return 0;
}

相关文章:

【算法学习】—n皇后问题(回溯法)
【算法学习】—n皇后问题(回溯法) 1. 什么是回溯法? 相信"迷宫"是许多人儿时的回忆,大家小时候一定都玩过迷宫游戏。我们从不用别人教,都知道走迷宫的策略是: 当遇到一个岔路口,会有以下两种情况…...

万亿OTA市场进入新爆发期,2025或迎中国汽车软件付费元年
伴随智能汽车市场规模发展,越来越多的汽车产品具备OTA能力,功能的优化、以及服务的差异化,成为了车企竞争的新战场。 例如,今年初,问界M5 EV迎来了首次OTA升级,升级内容覆盖用户在实际用车中的多个场景&am…...
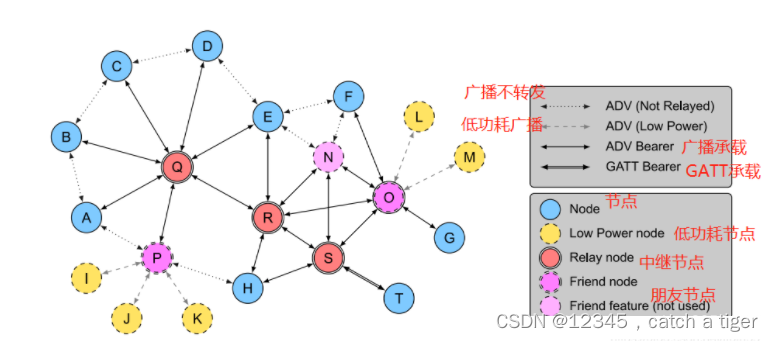
Android硬件通信之 蓝牙Mesh通信
一,简介 蓝牙4.0以下称为传统蓝牙,4.0以上是低功耗蓝牙,5.0开始主打物联网 5.0协议蓝牙最重要的技术就是Mesh组网,实现1对多,多对多的无线通信。即从点对点传输发展为网络拓扑结构,主要领域如灯光控制等&…...

PG数据库实现bool自动转smallint的方式
删除函数: 语法: DROP FUNCTION IF EXISTS your_schema_name.function_name(arg_type1, arg_type2) CASCADE RESTRICT; 实例: DROP FUNCTION IF EXISTS platformyw.boolean_to_smallint(bool) CASCADE RESTRICT; 查询是否存在函数 语法: SELE…...
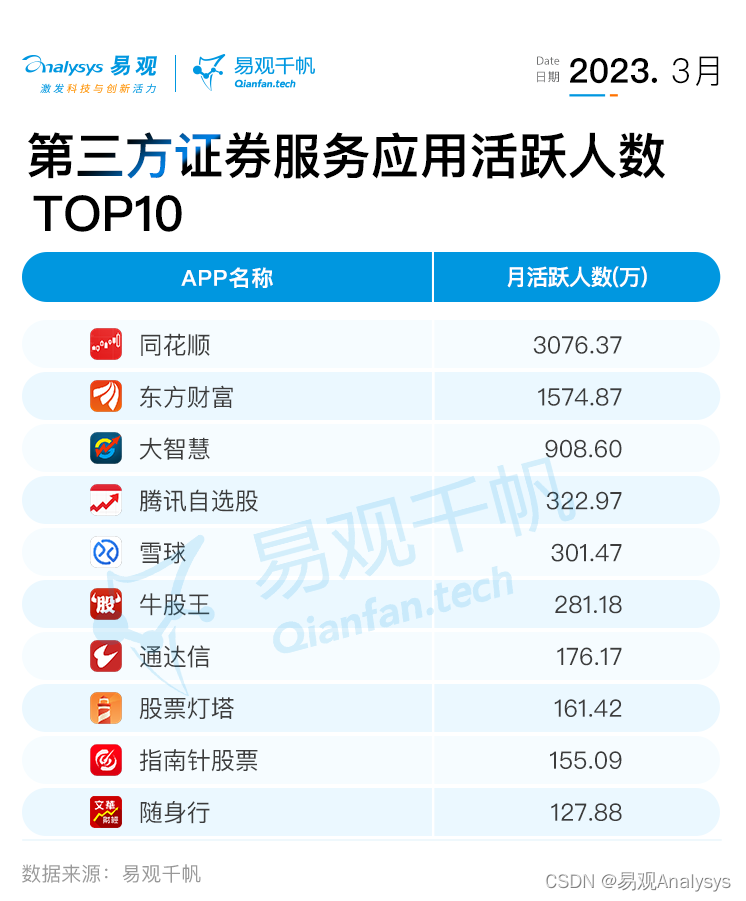
易观千帆 | 2023年3月证券APP月活跃用户规模盘点
易观:2023年3月证券服务应用活跃人数14131.58万人,相较上月,环比增长0.61%,同比增长0.60%;2023年3月自营类证券服务应用Top10 活跃人数6221.44万人,环比增长0.08%;2023年3月第三方证券服务应用T…...
2023年江苏专转本成绩查询步骤
2023年江苏专转本成绩查询时间 2023年江苏专转本成绩查询时间预计在5月初,参加考试的考生,可以关注考试院发布的消息。江苏专转本考生可在规定时间内在省教育考试院网,在查询中心页面中输入准考证号和身份证号进行查询,或者拨…...
函数)
JavaScript中sort()函数
sort()函数是javascript中自带函数,这个函数的功能是排序。 使用sort()函数时,函数参数如果不设置的话,以默认方式进行排序,就是以字母顺序进行排序,准确的讲就是按照字符编码的顺序进行排序。 var arr [3,2,3,34,1…...

泰克Tektronix DPO5204B混合信号示波器
特征 带宽:2 GHz输入通道:4采样率:1 或 2 个通道上为 5 GS/s、10 GS/s记录长度:所有 4 个通道 25M,50M:1 或 2 个通道上升时间:175 皮秒MultiView zoom™ 记录长度高达 250 兆点>250,000 wf…...
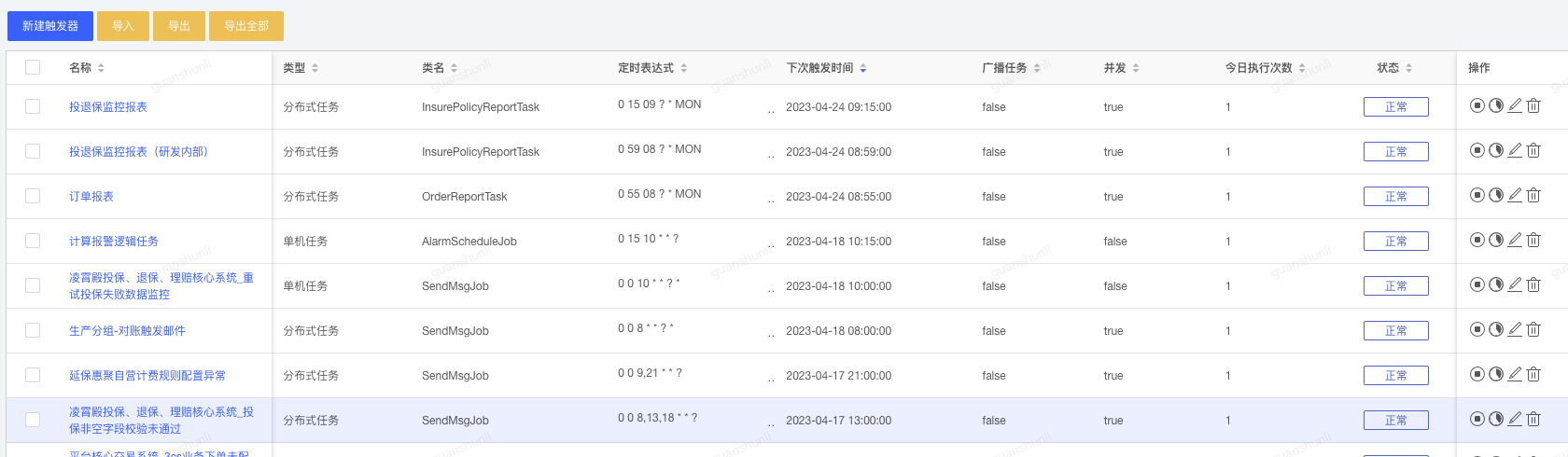
突破传统监测模式:业务状态监控HM的新思路
作者:京东保险 管顺利 一、传统监控系统的盲区,如何打造业务状态监控。 在系统架构设计中非常重要的一环是要做数据监控和数据最终一致性,关于一致性的补偿,已经由算法部的大佬总结过就不在赘述。这里主要讲如何去补偿ÿ…...

0Ω电阻在PCB板中的5大常见作用
在PCB板中,时常见到一些阻值为0Ω的电阻。我们都知道,在电路中,电阻的作用是阻碍电流,而0Ω电阻显然失去了这个作用。那它存在于PCB板中的原因是什么呢?今天我们一探究竟。 1、充当跳线 在电路中,0Ω电阻…...

分布式消息队列Kafka(三)- 服务节点Broker
1.Kafka Broker 工作流程 (1)zookeeper中存储的kafka信息 1)启动 Zookeeper 客户端。 [zrclasshadoop102 zookeeper-3.5.7]$ bin/zkCli.sh 2)通过 ls 命令可以查看 kafka 相关信息。 [zk: localhost:2181(CONNECTED) 2]…...

蠕动泵说明书_RDB
RDB_2T-S蠕 动 泵 概述 蠕动灌装泵是一种高性能、高质量的泵。采用先进的微处理技术及通讯方式做成的控制器和步进电机驱动器,配以诚合最新研制出的泵头,使产品在稳定性、先进性和性价比上达到一个新的高度。适用饮料、保健品、制药、精细化工等诸流量…...

浅谈react如何自定义hooks
react 自定义 hooks 简介 一句话:使用自定义hooks可以将某些组件逻辑提取到可重用的函数中。 自定义hooks是一个从use开始的调用其他hooks的Javascript函数。 下面以一个案例: 新闻发布操作,来简单说一下react 自定义 hooks。 不使用自定义hooks时 …...
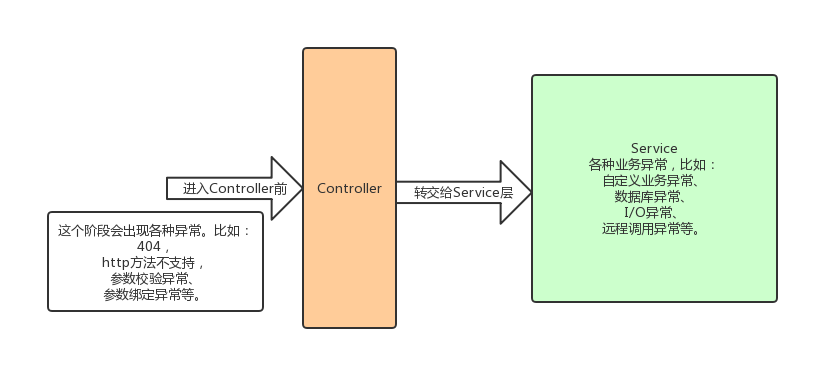
如何优雅的写个try catch的方式!
软件开发过程中,不可避免的是需要处理各种异常,就我自己来说,至少有一半以上的时间都是在处理各种异常情况,所以代码中就会出现大量的try {...} catch {...} finally {...} 代码块,不仅有大量的冗余代码,而…...
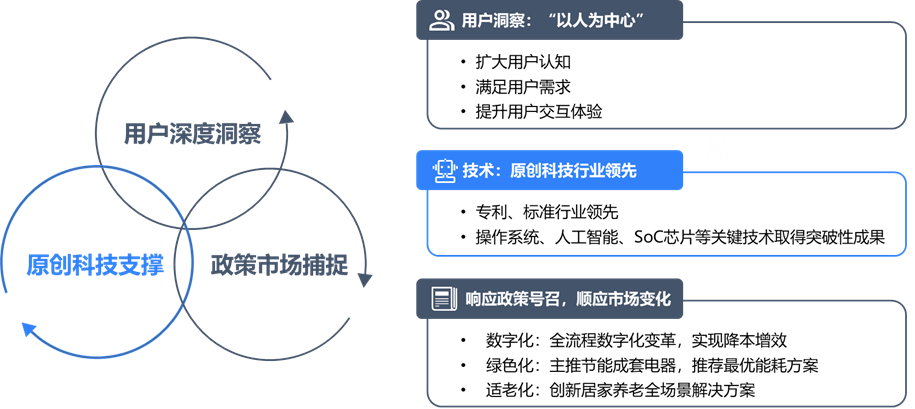
海尔智家:智慧场景掌握「主动」权,用户体验才有话语权
2023年1月,《福布斯》AI专栏作家Rob Toews发布了年度AI发展预测,指出人工智能的发展将带来涉及各行业、跨学科领域的深远影响。变革将至,全球已掀起生成式AI热,以自然语言处理为代表的人工智能技术在快速进化,积极拥抱…...

基于铜锁,在前端对登录密码进行加密,实现隐私数据保密性
本文将基于 铜锁(tongsuo)开源基础密码库实现前端对用户登录密码的加密,从而实现前端隐私数据的保密性。 首先,铜锁密码库是一个提供现代密码学算法和安全通信协议的开源基础密码库,在中国商用密码算法,例…...

LVS的小总结
LVS的工作模式及其工作过程: LVS 有三种负载均衡的模式,分别是VS/NAT(nat 模式)、VS/DR(路由模式)、VS/TUN(隧道模式)。 1、NAT模式(NAT模式) 原理&#x…...
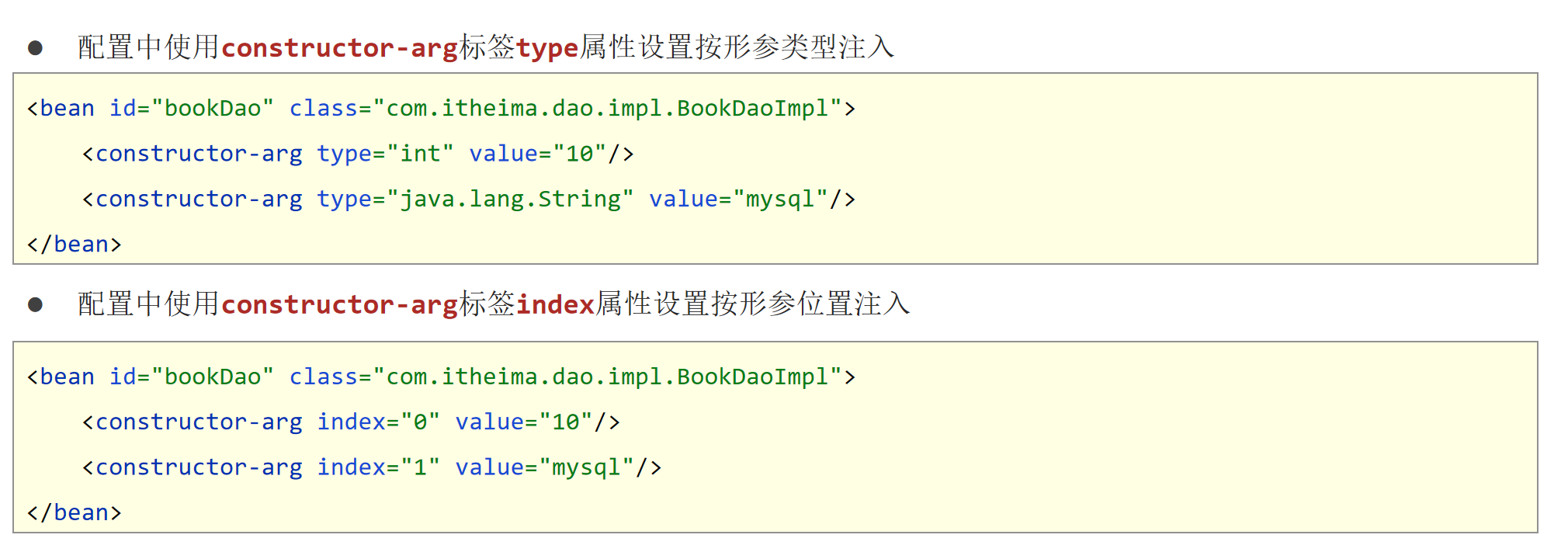
Spring依赖注入(DI配置)
Spring依赖注入 1. 依赖注入方式【重点】1.1 依赖注入的两种方式1.2 setter方式注入问题导入引用类型简单类型 1.3 构造方式注入问题导入引用类型简单类型参数适配【了解】 1.4 依赖注入方式选择 2. 依赖自动装配【理解】问题导入2.1 自动装配概念2.2 自动装配类型依赖自动装配…...
绘声绘影2023简体中文版新功能介绍
会声会影是一款专业的数字音频工作站软件,它提供强大的音频编辑和制作功能,被广泛应用于音乐创作、录音棚录制以及现场演出等领域。会声会影的最新版本会声会影2023将于2022年底发布,主要功能和新功能详述如下: 会声会影2023主要功能: 1. 直观易用的界面:会声会影采用简洁而不…...

一个好的前端开发人员必须掌握的前端代码整洁与开发技巧
前端代码整洁与开发技巧 为保证前端人员在团队项目开发过程中的规范化、统一化,特建立《前端代码整洁与开发技巧》文档,通过代码简洁推荐、开发技巧推荐等章节来帮助我们统一代码规范和编码风格,从而提升项目的可读性和可维护性。 目录 …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
