【刷题】搜索——BFS:城堡问题(The Castle)
目录
- 题目
- 代码(Flood Fill)
- 代码(并查集)
题目

题目链接
找出房间个数——>求连通块个数
最大房间——>求最大连通块
直接用flood fill算法
注意题目的输入,例如11=8+2+111=8+2+111=8+2+1,则代表有西、北、南墙

代码(Flood Fill)
上下左右的走向可以预先设置数组dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};
墙的表示相当于二进制编码,可以用位运算获取特定位的数值(p[t.x][t.y] >> i & 1
#include <iostream>
#define x first
#define y second
using namespace std;int n, m;
int p[55][55];
bool st[55][55];
typedef pair<int, int> PII;
PII q[2505];int bfs(int i, int j) {int hh = 0, tt = 0;int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};q[0] = {i, j};st[i][j] = true;while(hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; i ++ ) {int tx = t.x + dx[i], ty = t.y + dy[i];if (tx < 0 || tx >= m || ty < 0 || ty >= n) continue; // 越界 if (st[tx][ty]) continue; // 已经走过 if ((p[t.x][t.y] >> i) & 1) continue; // 是墙 q[ ++ tt ] = {tx, ty}; // 入队 st[tx][ty] = true;}}return tt + 1; // 队列同时有的元素个数,就是连通块大小
}int main () {scanf("%d%d", &m, &n);for (int i = 0; i < m; i ++ ) {for (int j = 0; j < n; j ++ ) {scanf("%d", &p[i][j]);} }int max_s = 0, cnt = 0;for (int i = 0; i < m; i ++ ) {for (int j = 0; j < n; j ++ ) {if (st[i][j]) continue;max_s = max(max_s, bfs(i, j));cnt ++;} }printf("%d\n%d\n", cnt, max_s);return 0;
}代码(并查集)
将房间连通也可用并查集,枚举每个房间和两个方向(东、南;西、北;西、南;东、北皆可),如果没墙则连通,集合总数-1,集合元素个数相加。
注意集合元素个数初始都是1,ares初始也为1,因为连通块最小也有1个房间
#include <iostream>
using namespace std;int m, n;
int g[55][55];
const int dx[2] = {1, 0}, dy[2] = {0, 1}; // 向南、向东
const int dw[2] = {8, 4}; // 南墙、东墙int p[2505], np[2505];
int find(int x) {if (p[x] != x) p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &m, &n);for (int i = 0; i < m; i ++ ) {for (int j = 0; j < n; j ++ ) {scanf("%d", &g[i][j]);}}for (int i = 0; i < m * n; i ++ ) p[i] = i, np[i] = 1;int cnt = m * n, ares = 1;for (int i = 0; i < m; i ++ ) {for (int j = 0; j < n; j ++ ) {for (int k = 0; k < 2; k ++ ) {int tx = i + dx[k], ty = j + dy[k];if (tx >= m || ty >= n) continue; if (g[i][j] & dw[k]) continue; // 是墙 int a = find(i * n + j), b = find(tx * n + ty); // 找到{i,j}和{tx,ty}的祖先 if (a != b) {p[a] = b; // a合并到b cnt -- ; // 集合总数-1 np[b] += np[a]; // a元素加到b ares = max(ares, np[b]);}}}}printf("%d\n%d\n", cnt, ares);return 0;
}
相关文章:

【刷题】搜索——BFS:城堡问题(The Castle)
目录题目代码(Flood Fill)代码(并查集)题目 题目链接 找出房间个数——>求连通块个数 最大房间——>求最大连通块 直接用flood fill算法 注意题目的输入,例如118211182111821,则代表有西、北、南墙…...

深度学习——torch相关函数用法解析
1. torch.ones() torch.ones(*sizes, outNone) → Tensor函数功能:返回一个全为1 的张量,形状由可变参数sizes定义。 参数: sizes (int…) – 整数序列,定义了输出形状 out (Tensor, optional) – 结果张量 例子: >>> …...
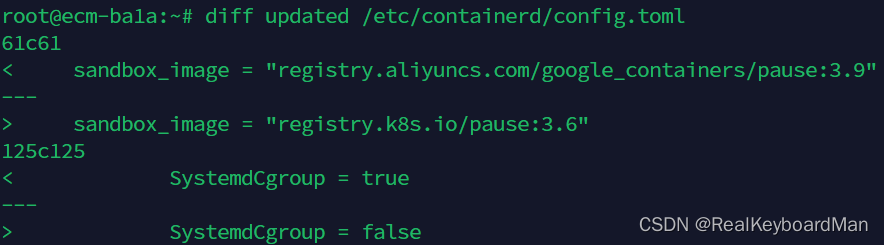
ubuntu 20使用kubeadm安装k8s 1.26
步骤 机器:4核8G,root账号,可访问互联网 1、更新apt apt-get update 2、安装一些基本工具 apt-get install ca-certificates curl gnupg lsb-release net-tools apt-transport-https 3、ifconfig 获取ip,hostname获取主机名&…...

低代码开发平台|制造管理-生产过程管理搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建制造管理-生产过程。1.2、应用场景先填充工序信息,再设置工艺路线对应的工序;工序信息及工艺路线列表报表展示的是所有工序、工艺路线信息,可进行新增对应数据的操作。2、设置方法2.1、表…...
python对多个csv文件进行合并(表头需一致)
之前写过python对【多个Excel文件】中的【单个sheet】进行合并,参考:点我 之前也写过python对【多个Excel文件】中的【多个sheet】进行合并,参考:点我 今天再写一个python对多个csv格式的文件进行合并的小工具 但是大家切记&am…...

Salesforce Apex调用邮件模板
正常调用无模板:mail.setToAddresses(new List<String>{user.Email});//mail.setReplyTo(444298824qq.com);//mail.setCcAddresses(null);mail.setSenderDisplayName(EOP系统);mail.setSubject(EOP通知(待审批):您有未处理的…...
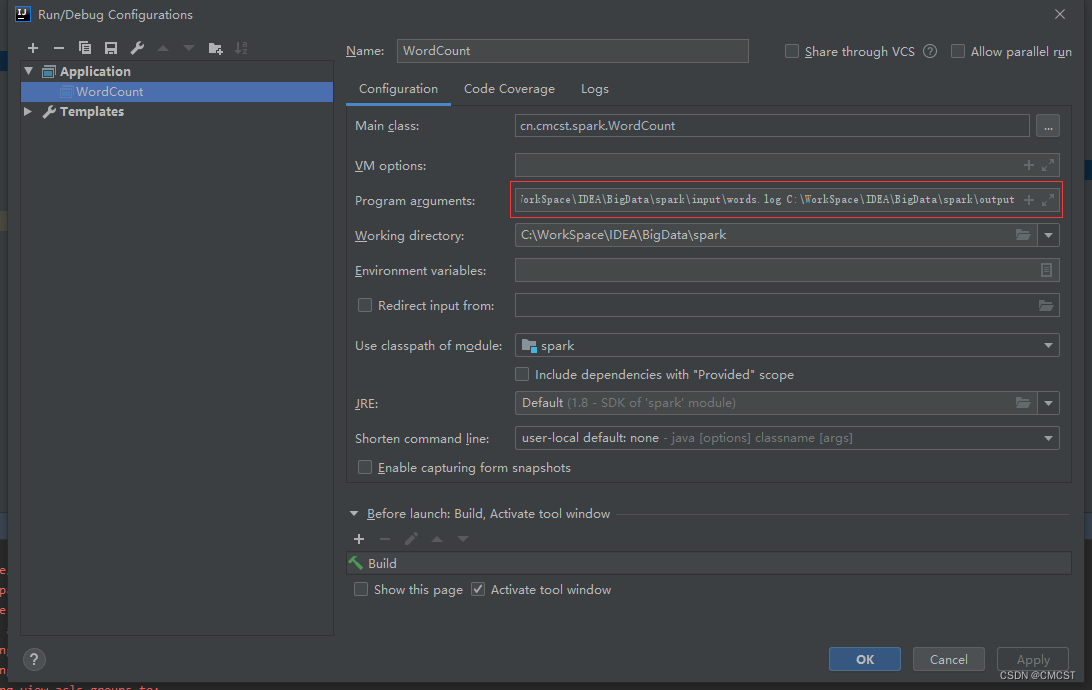
windows本地开发Spark[不开虚拟机]
1. windows本地安装hadoop hadoop 官网下载 hadoop2.9.1版本 1.1 解压缩至C:\XX\XX\hadoop-2.9.1 1.2 下载动态链接库和工具库 1.3 将文件winutils.exe放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.4 将文件hadoop.dll放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.5 将文件hadoop.dl…...

一文教你快速估计个股交易成本
交易本身对市场会产生影响,尤其是短时间内大量交易,会影响金融资产的价格。一个订单到来时的市场价格和订单的执行价格通常会有差异,这个差异通常被称为交易成本。在量化交易的策略回测部分,不考虑交易成本或者交易成本估计不合理…...

Leetcode—移除元素、删除有序数组中的重复项、合并两个有序数组
移除元素 此题简单,用双指针方法即可, 如果右指针指向的元素不等于val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移; 如果右指针指向的元素等于 val&…...
大疆 安全开发 C++1面)
面试(十)大疆 安全开发 C++1面
1. 在C++开发中定义一个变量,若不做初始化直接使用会怎样? 如果该变量是一个普通变量,则如果对其进行访问,会返回一个随机值,int类型不一定为0,bool类型也不一定为false 如果该变量为一个静态变量,则初始值都是一个0; 如果该变量是一个指针,那么在后续程序运行中很…...
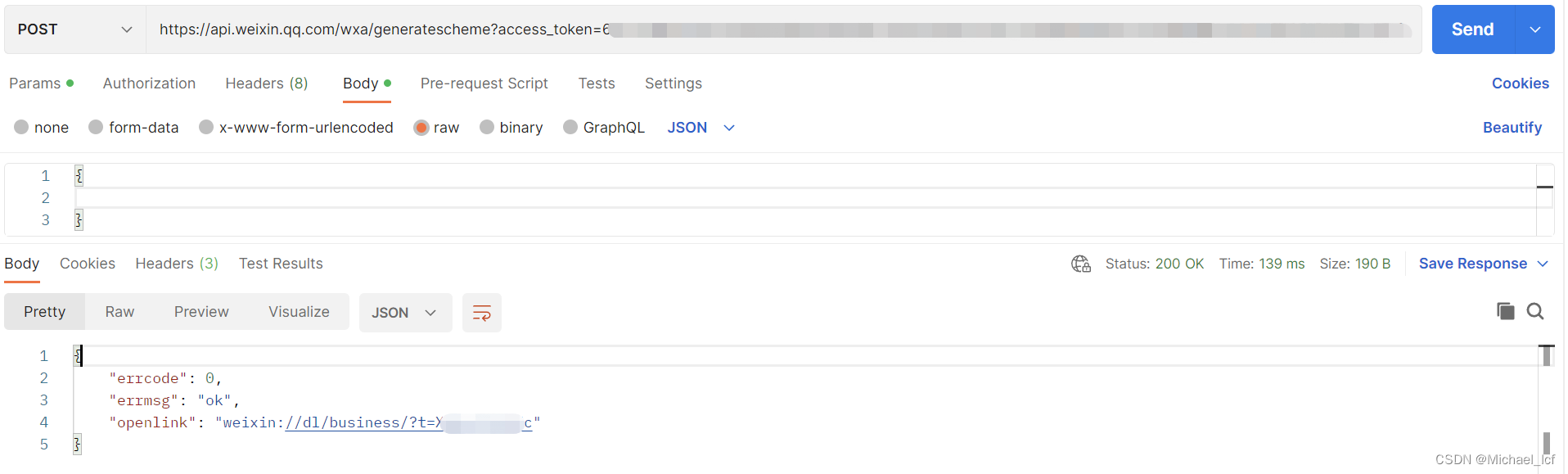
短信链接跳转微信小程序
短信链接跳转微信小程序1 实现方案1.1 通过URL Scheme实现1.2 通过URL Link实现1.3 通过云开发静态网站实现2 实现方案对比3 实践 URL Schema 方案3.1 获取微信access_token3.2 获取openlink3.3 H5页面(模拟短信跳转,验证ok)4 问题小节4.1 io…...

吉林电视台启用乾元通多卡聚合系统广电视频传输解决方案
随着广播电视数字化、IP化、智能化的逐步深入,吉林电视台对技术改造、数字设备升级提出了更高要求,通过对系统性能、设计理念的综合评估,正式启用乾元通多卡聚合系统广电视频传输解决方案,将用于大型集会、大型演出、基层直播活动…...
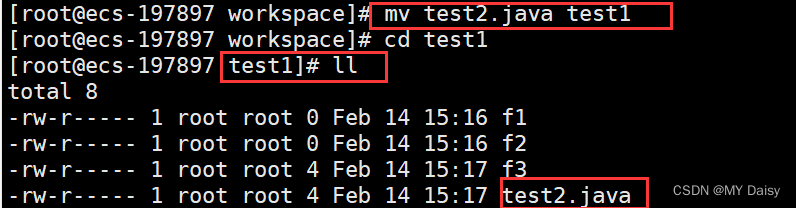
Linux常用命令1
目录1、远程登陆服务器2、文件相关(1)文件和目录属性(2)创建目录mkdir(3)删除目录rmdir(4)创建文件touch(5)删除文件或目录rm(6)ls命令…...

【C++进阶】一、继承(总)
目录 一、继承的概念及定义 1.1 继承概念 1.2 继承定义 1.3 继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、菱形继承及菱形虚拟继承 7.1 继承的分类 7.2 菱形虚拟…...
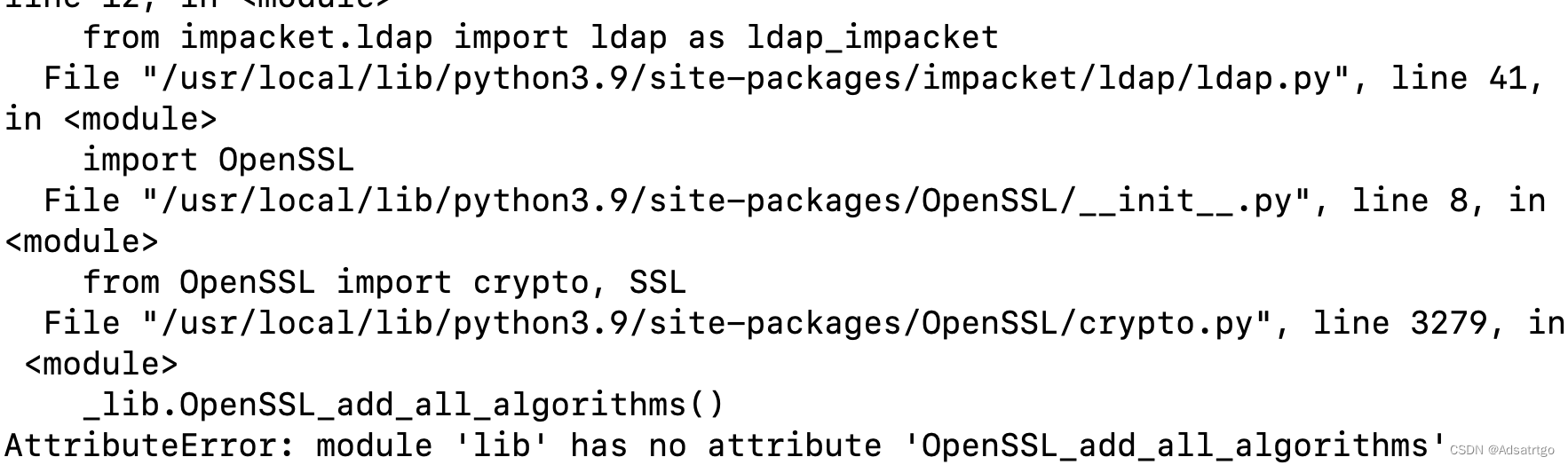
AttributeError: module ‘lib‘ has no attribute ‘OpenSSL_add_all_algorithms
pip安装crackmapexec后,运行crackmapexec 遇到报错 AttributeError: module lib has no attribute OpenSSL_add_all_algorithms 直接安装 pip3 install crackmapexec 解决 通过 python3 -m pip install --upgrade openssl 或者 python3 -m pip install openssl>22.1.…...

Python实现视频自动打码功能,避免看到羞羞的画面
前言 嗨呀嗨呀,最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就会看到一堆马赛克,由于太好奇了就找了一下原因,结果是因为某艺人塌房了…虽然但是 看综艺的时候满影响美观的 咳咳,这里我可不是来教你们如何解…...
说说Knife4j
Knife4j是一款基于Swagger2的在线API文档框架使用Knife4j, 需要 添加Knife4j的依赖当前建议使用的Knife4j版本, 只适用于Spring Boot2.6以下版本, 不含Spring Boot2.6 在主配置文件(application.yml)中开启Knife4j的增强模式必须在主配置文件中进行配置, 不要配置在个性化配置文…...
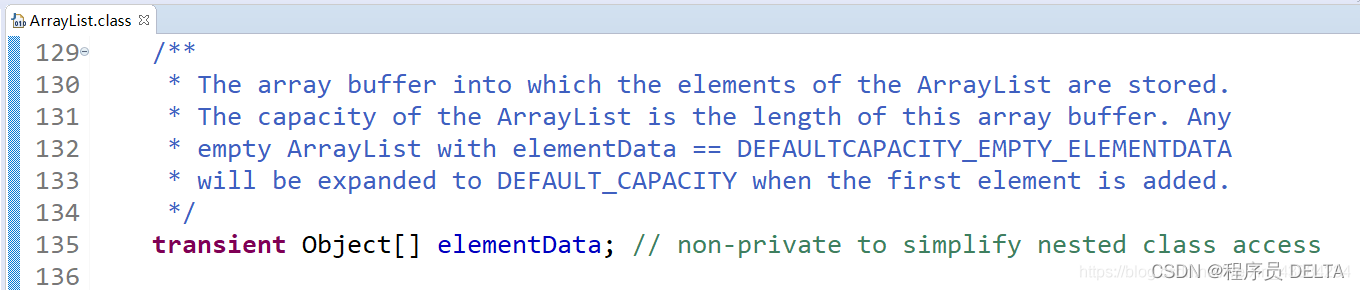
Java学习笔记-03(API阶段-2)集合
集合 我们接下来要学习的内容是Java基础中一个很重要的部分:集合 1. Collection接口 1.1 前言 Java语言的java.util包中提供了一些集合类,这些集合类又称之为容器 提到容器不难想到数组,集合类与数组最主要的不同之处是,数组的长度是固定的,集合的长度是可变的&a…...
)
「3」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 矩阵的秩 定义4:在mxn矩阵A中,任取k行与k列(k<m,k<n),位…...
)
【CSDN竞赛】27期题解(Javascript)
前言 本来排名是20的,不过第一题有点输出bug,最后实际测出来又重新排名,刚好卡在第10。但是考试报告好像过了12小时就下载不到了,所以就只写题目求解的JS函数吧。 1. 幸运数字 小艺定义一个幸运数字的标准包含3条: 仅包含4或7幸…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
