有符号数和无符号数左移和右移
主要是有符号数的左移。
有的说不管符号位,直接左移,所以可以一会正数一会复数
https://bbs.csdn.net/topics/391075092
有的说符号位不动,其他来左移
不明白了。。。。
https://blog.csdn.net/hnjzsyjyj/article/details/119721014
https://wenku.baidu.com/view/6e31935402f69e3143323968011ca300a6c3f60d.html?wkts=1682661838416
算术移位对应有符号位数,逻辑移位对应无符号位数
左移与符号无关,都是逻辑左移(对应SHL指令),而右移无符号数做逻辑右移(对应SHR指令)、有符号数做算术右移(对应SAR指令)。 不过这也是与语言相关的,在Pascal中,移位一律是逻辑移位,算术移位要用乘除。
对于无符号数的左移和右移,因为不涉及到符号位的问题,比较好理解:
左移低位补零,高位舍弃
右移高位补零,低位舍弃
对于有符号数的左移和右移,因为符号位的参与,可能各个编译器的实现方式上有差别
我在/home/utils/gcc-5.2.0/bin/g++ 这个g++编译器的版本上试了下:
左移低位补零,高位舍弃(和无符号数的实现相同),这意味着本来一个正数,在移位的过程中,可能一会儿变成负数,一会儿又变回正数,然后再变负数···这种跳跃的情况。
右移高位补符号位,低位舍弃。所以如果一个int类型的-1, 进行右移操作,无论进行多少次,结果仍然为-1,因为-1 = 1111 1111 1111 1111 1111 1111 1111 1111b.
另外,char类型,其实是一个int8_t类型,是一个有符号的8bit整数类型。
————————————————
:https://blog.csdn.net/baidu_35679960/article/details/124510929
相关文章:

有符号数和无符号数左移和右移
主要是有符号数的左移。 有的说不管符号位,直接左移,所以可以一会正数一会复数 https://bbs.csdn.net/topics/391075092 有的说符号位不动,其他来左移 不明白了。。。。 https://blog.csdn.net/hnjzsyjyj/article/details/119721014 https://…...
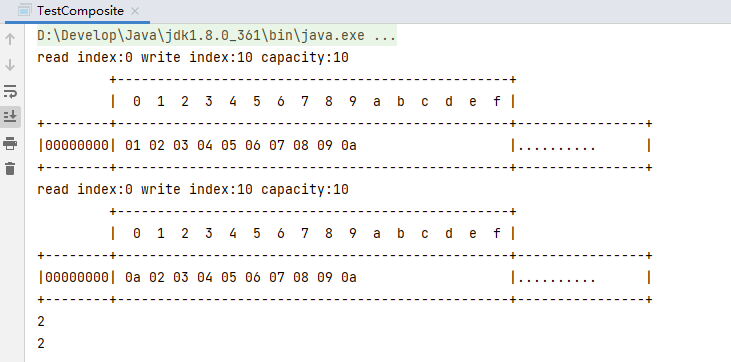
Netty小白入门教程
一、概述 1.1 概念 Netty是一个异步的基于事件驱动(即多路复用技术)的网络应用框架,用于快速开发可维护、高性能的网络服务器和客户端。 1.2 地位 Netty在Java网络应用框架中的地位就好比,Spring框架在JavaEE开发中的地位。 以下的框架都使用了Nett…...

【逻辑位移和算数位移】
<< 运算符 && >> 运算符 正数位移 当 x>>n 中 x 为正数时,会将x的所有位右移x位,同时左边高位补0 显而易见,运算结束后,值为1 。 可知右移n位,结果就是 x / 2^n:7 / 2 ^2 1;…...
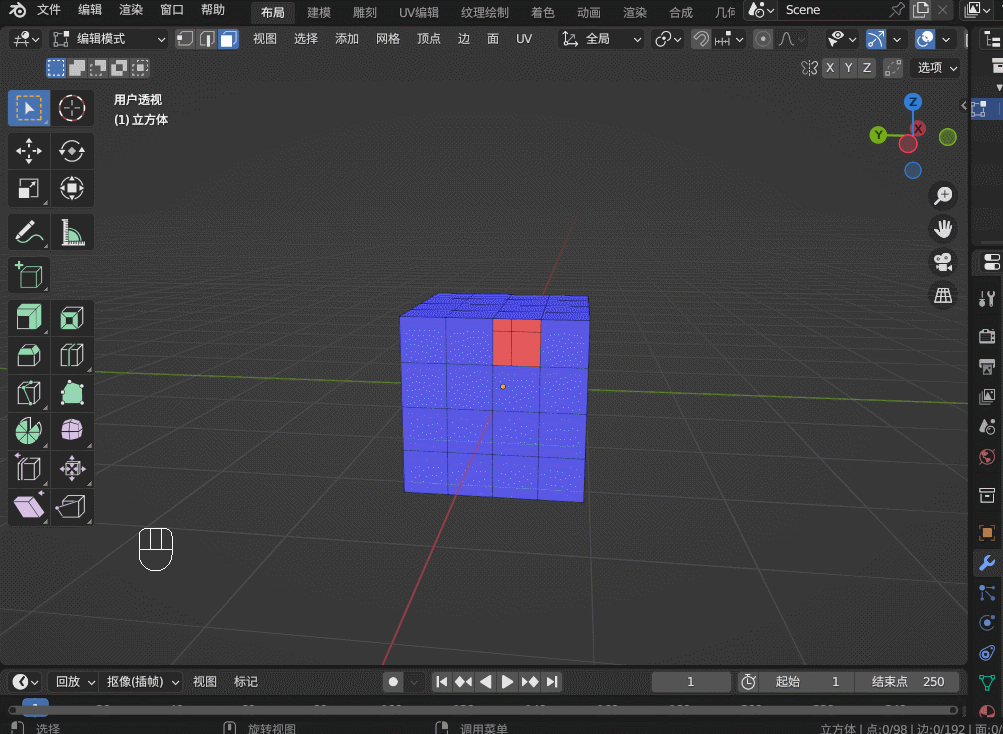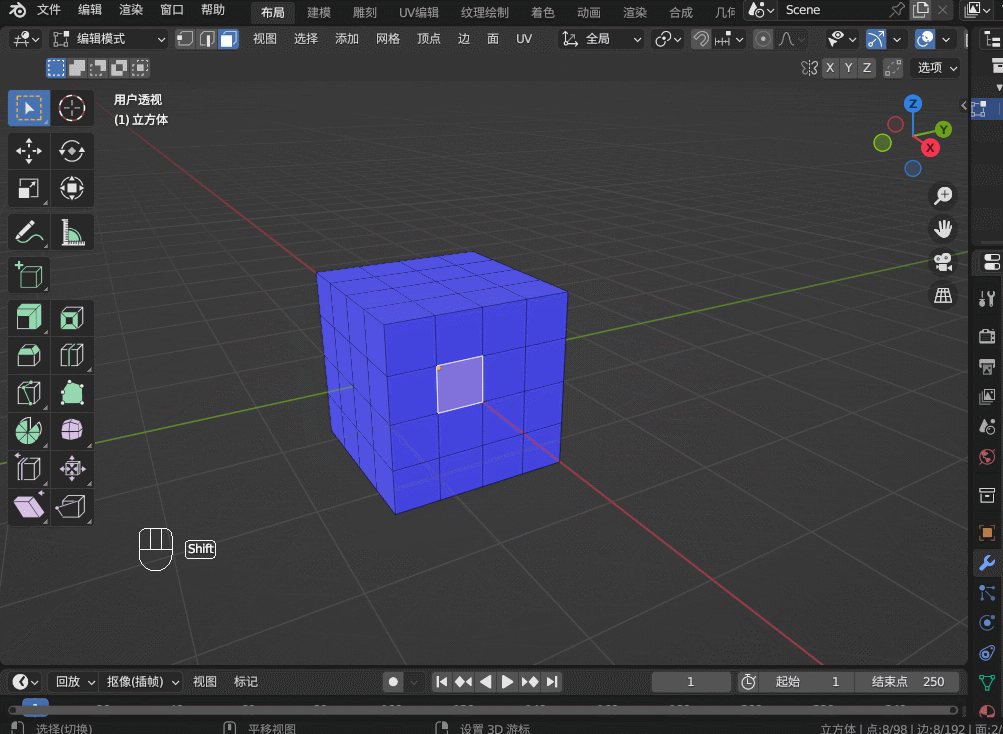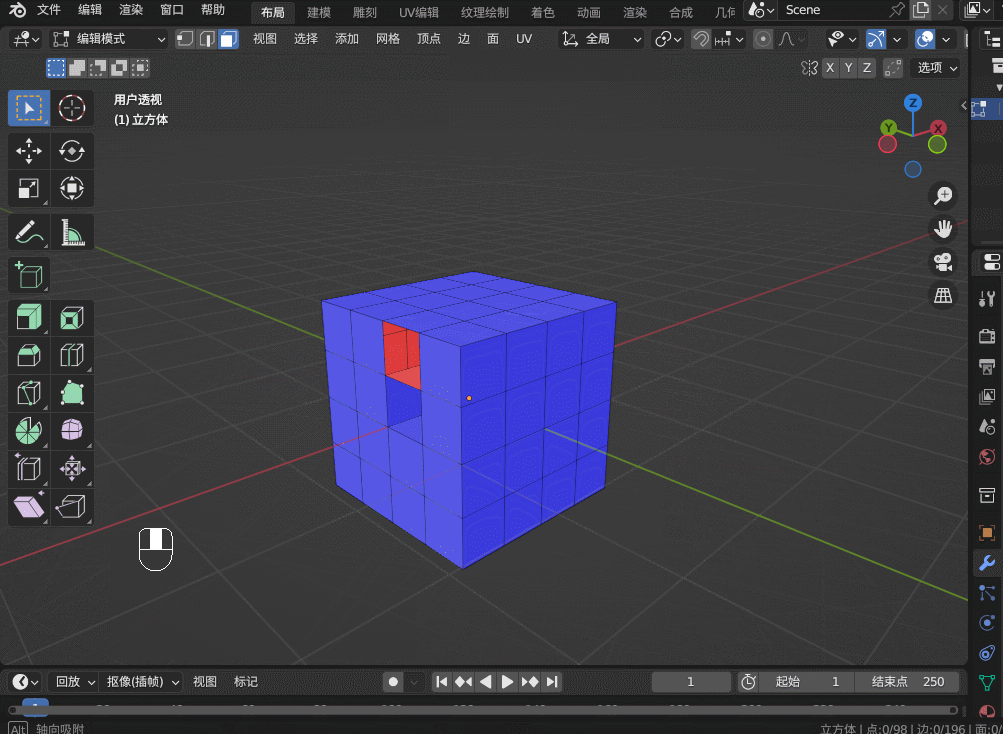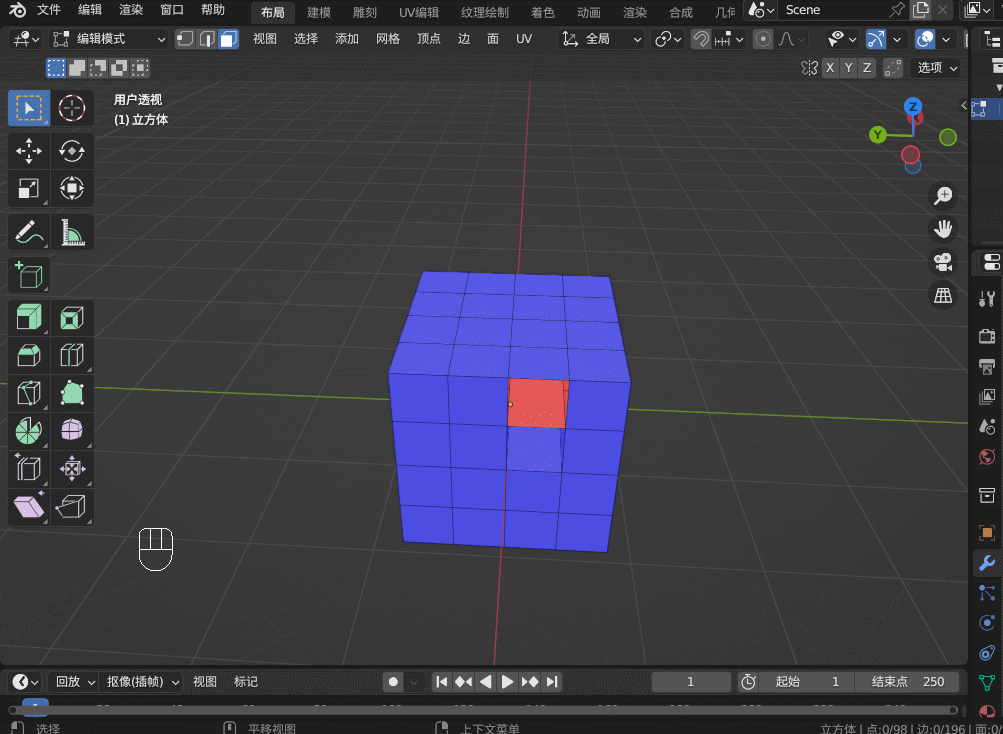
Blender3.5 边的操作
目录 1. 边操作1.1 边的细分 Subdivide1.2 边的滑移 Edge Slide1.3 边的删除1.4 边的溶解 Dissolve1.5 边线倒角 Bevel1.6 循环边 Loop Edges1.7 并排边 Ring Edges1.8 桥接循环边 1. 边操作 1.1 边的细分 Subdivide 在边选择模式,选中一条边,右键&…...

Java与Python、Node.js在人工智能和区块链应用程序开发中的比较
背景 Java、Python和Node.js都是常用的编程语言,它们在不同领域都有广泛的应用。在人工智能和区块链应用程序开发中,这三种语言都具有各自的优势和劣势。 Java的优势 Java在企业级应用中应用广泛,这得益于其跨平台性、安全性和稳定性等特点。在人工智能和区块链应用程序开…...

【计算机是怎么跑起来的】基础:计算机三大原则
【计算机是怎么跑起来的】基础:计算机三大原则 计算机的三个根本性基础1.计算机是执行输入,运算,输出的机器输入,运算,输出 2. 软件是指令和数据的集合指令数据 3. 计算机的处理方式有时与人们的思维习惯不同对计算机来…...
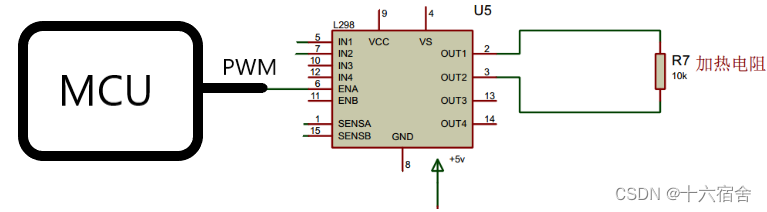
NXP公司LPC21XX+PID实现稳定温度控制
本例使用的是LPC21XX系列芯片提供的PWM功能实现稳定的温度控制。首先我们获得当前环境温度之后,再用设定的温度与当前温度相减,通过PID算法计算出当前输出脉宽,并将其输出到L298N模块中,使加热丝发热,形成闭环…...

【CE实战-生化危机4重置版】实现角色瞬移、飞翔
▒ 目录 ▒ 🛫 导读需求开发环境1️⃣ CE扫描内存,定位坐标地址(加密后的地址)2️⃣ 硬件写入断点,定位真实坐标地址内存写入断点,定位到访问地址分析代码...

强烈建议互联网人转战实体和农业,去了就是降维打击!实体太缺人才了,老板也不缺钱!...
大环境不好,互联网人该何去何从? 一位网友提出了一个新思路:强烈建议互联网同学转战实体、农业这些行业。实体真的太缺人才了,目前大部分实体都留下70后、80后在继续奋斗。其实实体老板很多都不缺钱,经过多年积累&…...

如何将 github pages 迁移到 vercel 上托管
如何将 github pages 迁移到 vercel 上托管 前言 早期网站使用 github pages,后来迁移到 coding,最近又放到腾讯云网站静态托管,无论是 coding 的 cos 存储桶,还是静态网站托管 他们都是收费的,那有没有免费的托管商呢,既不影响网站的访问速度还免费,于是,找了一下,还真有,ve…...

2023五一数学建模竞赛(五一赛)选题建议
提示:DS C君认为的难度:C<A<B,开放度:B<A<C 。 A题:无人机定点投放问题 这道题是传统的物理类题目,基本每次建模竞赛都会有。由于这道题目并未给明数据,所以数据获取和搜集资料是…...
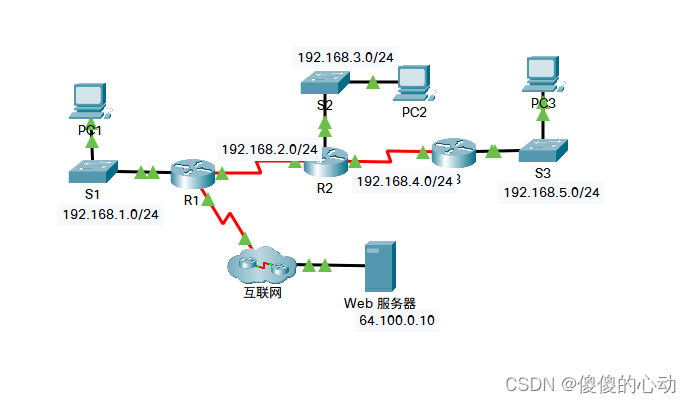
Packet Tracer - 配置 RIPv2
Packet Tracer - 配置 RIPv2 目标 第 1 部分:配置 RIPv2 第 2 部分:验证配置 拓扑图 背景信息 尽管在现代网络中极少使用 RIP,但是作为了解基本网络路由的基础则十分有用。 在本活动中,您将使用适当的网络语句和被动接口配置…...
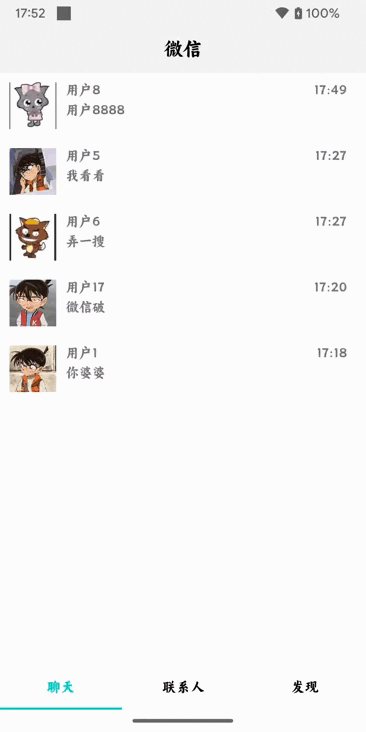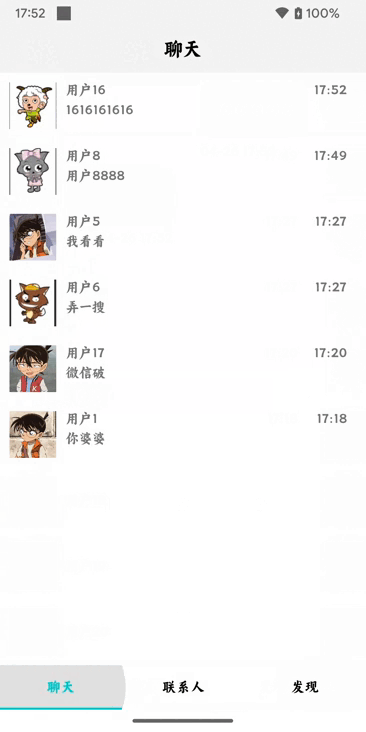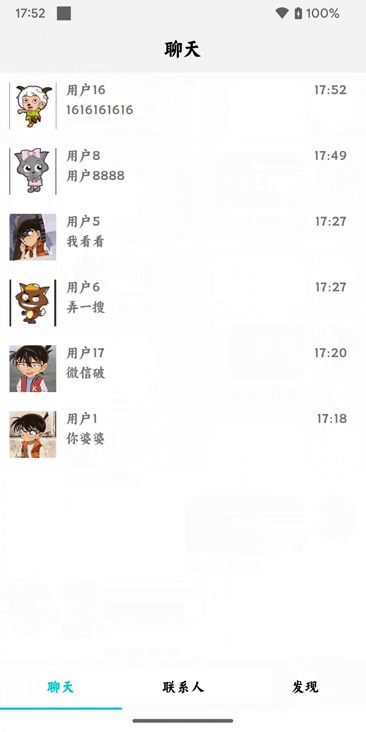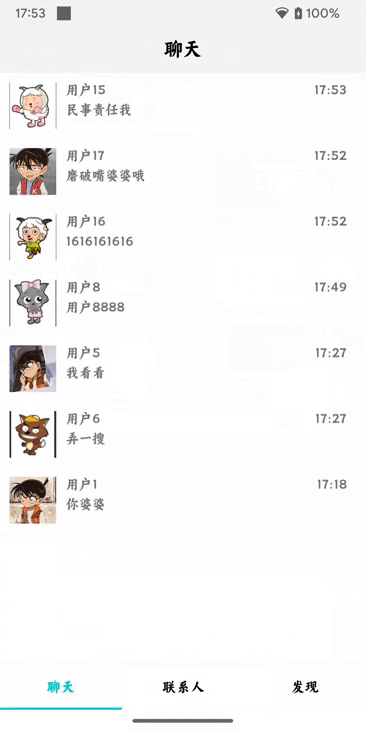
Android类似微信聊天页面教程(Kotlin)四——数据本地化
前提条件 安装并配置好Android Studio Android Studio Electric Eel | 2022.1.1 Patch 2 Build #AI-221.6008.13.2211.9619390, built on February 17, 2023 Runtime version: 11.0.150-b2043.56-9505619 amd64 VM: OpenJDK 64-Bit Server VM by JetBrains s.r.o. Windows 11 …...
C/C++基础知识
专栏:C/C 个人主页: C/C基础知识 前言C关键字(C98)命名空间命名空间的定义正常的命名空间的定义如何使用命名空间 命名空间可以嵌套同一个工程中允许存在多个相同名称的命名空间,编译器最后会合成同一个命名空间中(一个工程中的.h文件和test.…...

Java 入门 - 语法基础
hello world public class Hello {public static void main(String[] args) {System.out.println("hello world");} } 复制代码 public: 是关键字;表示公开的class: 是关键字;用来定义类Hello: 是类名;大小写敏感;命名…...

Java线程池及拒绝策略详解
前文提到线程的使用以及线程间通信方式,通常情况下我们通过new Thread或者new Runnable创建线程,这种情况下,需要开发者手动管理线程的创建和回收,线程对象没有复用,大量的线程对象创建与销毁会引起频繁GC,…...
GitLABJenkins
GitLAB & Jenkins 目录 实践:基于Jenkins提交流水线(测试成功)-2023.4.25 目的:掌握通过触发器将GitLab和Jenkins集成,实现提交流水线。 1、触发Jenkins构建 安装Generic Webhook Trigger插件 重启后,进入一个Pipeline项目设…...
)
互联网摸鱼日报(2023-04-26)
互联网摸鱼日报(2023-04-26) InfoQ 热门话题 神州数码:抢抓云原生发展机遇,共建共治共享 OpenNJet 应用引擎开源生态 《产业数字人才研究与发展报告(2023)》 如何写出CPU友好的代码,百倍提升…...
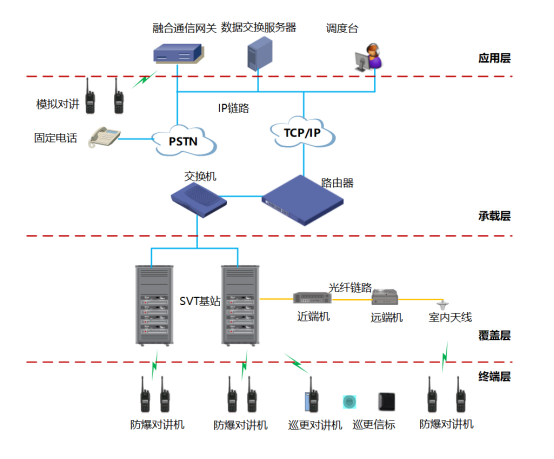
石化企业数字化防爆融合通信解决方案
项目背景 石化工业是我国国民经济和社会发展的基础性、战略性产业,其发展和壮大受到了党和国家的高度重视。随着石化企业厂区规模的不断扩大以及技术的快速发展,现有石化企业专网通信系统建设相对滞后,缺乏结合人员管理、安全生产、安全通信…...
)
NTT学习笔记(快速数论变换)
一些概念 欧拉函数 ϕ ( n ) \phi(n) ϕ(n) 欧拉函数简介 阶 若 g g g和 n n n互质,则令 g x % n 1 g^x\%n1 gx%n1的最小正整数 x x x称为 g g g模 n n n的阶。 原根 对于互质的两个正整数 g g g和 n n n,如果 g g g模 n n n的阶为 ϕ ( n ) \phi…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
