NTT学习笔记(快速数论变换)
一些概念
欧拉函数 ϕ ( n ) \phi(n) ϕ(n)
欧拉函数简介
阶
若 g g g和 n n n互质,则令 g x % n = 1 g^x\%n=1 gx%n=1的最小正整数 x x x称为 g g g模 n n n的阶。
原根
对于互质的两个正整数 g g g和 n n n,如果 g g g模 n n n的阶为 ϕ ( n ) \phi(n) ϕ(n),则称 g g g为 n n n的原根。
求原根
一般的原根都比较小,暴力枚举即可。
NTT
在 F F T FFT FFT中,我们选择 n n n次单位复根作为 x x x的值,因为他们满足消去引理、折半引理、求和引理,所以可以用分治的方法将时间复杂度变为 O ( n log n ) O(n\log n) O(nlogn)。但因为用了复数,所以在精度上有误差。而在一些题目要求的是带模的多项式乘法,所以 F F T FFT FFT就用不了了。那么,我们能不能让 x x x取整数值,使得这个值也能满足消去引理、折半引理、求和引理呢?
设 ϕ ( m ) = r × 2 d \phi(m)=r\times 2^d ϕ(m)=r×2d,令 n = 2 d n=2^d n=2d, x n i = x ϕ ( m ) × i / n ( m o d m ) x_n^i=x^{\phi(m)\times i/n}\pmod m xni=xϕ(m)×i/n(modm),其中 i ≤ n i\leq n i≤n
则 x n i x_n^i xni有以下性质:
1. 消去引理
x d n d k = x n k ( m o d m ) x_{dn}^{dk}=x_n^k\pmod m xdndk=xnk(modm)
证明: x d n d k = x ϕ ( m ) × d k / d n = x ϕ ( m ) × k / n = x n k ( m o d m ) x_{dn}^{dk}=x^{\phi(m)\times dk/dn}=x^{\phi(m)\times k/n}=x_n^k\pmod m xdndk=xϕ(m)×dk/dn=xϕ(m)×k/n=xnk(modm)
2. 折半引理
( x n k + n / 2 ) 2 = x n / 2 k ( m o d m ) (x_n^{k+n/2})^2=x_{n/2}^k \pmod m (xnk+n/2)2=xn/2k(modm)
证明: ( x n k + n / 2 ) 2 = x n 2 k + n = x n 2 k = x n / 2 k ( m o d m ) (x_n^{k+n/2})^2=x_n^{2k+n}=x_n^{2k}=x_{n/2}^k\pmod m (xnk+n/2)2=xn2k+n=xn2k=xn/2k(modm)
3. 求和引理
∑ i = 0 n − 1 ( x n k ) j = 0 ( m o d m ) \sum\limits_{i=0}^{n-1}(x_n^k)^j=0\pmod m i=0∑n−1(xnk)j=0(modm)
证明: ∑ i = 0 n − 1 ( x n k ) j = 1 − ( x n k ) n 1 − x n k = 0 1 − x n k = 0 \sum\limits_{i=0}^{n-1}(x_n^k)^j=\dfrac{1-(x_n^k)^n}{1-x_n^k}=\dfrac{0}{1-x_n^k}=0 i=0∑n−1(xnk)j=1−xnk1−(xnk)n=1−xnk0=0
那么,用 x x x来代替 F F T FFT FFT中的 ω \omega ω,其他不变,就可以求带模数的多项式乘法了。
模数的限制
若模数 m = r × 2 k + 1 m=r\times 2^k+1 m=r×2k+1(其中 r r r为奇数, k k k为整数),则多项式乘积的次数不能超过 2 k 2^k 2k。
如果题目没有模数,那也可以取一个较大的模数,保证答案的每一位都小于这个模数,用这个模数来做 N T T NTT NTT也是可以的。
一些模数的原根
| 模数 | 原根 | 最大长度 |
|---|---|---|
| 998244353 = 119 × 2 23 + 1 998244353=119\times 2^{23}+1 998244353=119×223+1 | 3 3 3 | 2 23 2^{23} 223 |
| 469762049 = 7 × 2 26 + 1 469762049=7\times 2^{26}+1 469762049=7×226+1 | 3 3 3 | 2 26 2^{26} 226 |
| 2281701377 = 17 × 2 27 + 1 2281701377=17\times 2^{27}+1 2281701377=17×227+1 | 3 3 3 | 2 27 2^{27} 227 |
例题
多项式乘法(FFT)
#include<bits/stdc++.h>
using namespace std;
const long long g=3,mod=998244353;
long long w,wn,a1[5000005],a2[5000005];
long long mi(long long t,long long v){if(v==0) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void ch(long long *a,int l){for(int i=1,j=l/2,k;i<l-1;i++){if(i<j) swap(a[i],a[j]);k=l/2;while(j>=k){j-=k;k>>=1;}j+=k;}
}
void ntt(long long *a,int l,int fl){for(int i=2;i<=l;i<<=1){if(fl==1) wn=mi(g,(mod-1)/i);else wn=mi(g,mod-1-(mod-1)/i);for(int j=0;j<l;j+=i){w=1;for(int k=j;k<j+i/2;k++,w=w*wn%mod){long long t=a[k],u=w*a[k+i/2]%mod;a[k]=(t+u)%mod;a[k+i/2]=(t-u+mod)%mod;}}}if(fl==-1){long long ny=mi(l,mod-2);for(int i=0;i<l;i++) a[i]=a[i]*ny%mod;}
}
int main()
{int n=1,l1,l2;scanf("%d%d",&l1,&l2);++l1;++l2;while(n<l1+l2) n<<=1;for(int i=0;i<l1;i++){scanf("%lld",&a1[i]);}for(int i=0;i<l2;i++){scanf("%lld",&a2[i]);}ch(a1,n);ch(a2,n);ntt(a1,n,1);ntt(a2,n,1);for(int i=0;i<n;i++){a1[i]=a1[i]*a2[i]%mod;}ch(a1,n);ntt(a1,n,-1);for(int i=0;i<l1+l2-1;i++) printf("%lld ",a1[i]);return 0;
}
相关文章:
)
NTT学习笔记(快速数论变换)
一些概念 欧拉函数 ϕ ( n ) \phi(n) ϕ(n) 欧拉函数简介 阶 若 g g g和 n n n互质,则令 g x % n 1 g^x\%n1 gx%n1的最小正整数 x x x称为 g g g模 n n n的阶。 原根 对于互质的两个正整数 g g g和 n n n,如果 g g g模 n n n的阶为 ϕ ( n ) \phi…...
Android类似微信首页的页面开发教程(Kotlin)二
前提条件 安装并配置好Android Studio Android Studio Electric Eel | 2022.1.1 Patch 2 Build #AI-221.6008.13.2211.9619390, built on February 17, 2023 Runtime version: 11.0.150-b2043.56-9505619 amd64 VM: OpenJDK 64-Bit Server VM by JetBrains s.r.o. Windows 11 …...

PAt A1015 Reversible Primes
1015 Reversible Primes 分数 20 作者 CHEN, Yue 单位 浙江大学 A reversible prime in any number system is a prime whose "reverse" in that number system is also a prime. For example in the decimal system 73 is a reversible prime because its rever…...

解决Lemuroid识别不到蓝牙键盘的问题
Android系统基于libretro的全能游戏模拟器,目前有RetroArch,Kodi,Lemuroid。 而且这三个都是开源免费的APP。 Lemuroid相对前面两个功能比较简陋。也不能自己下载核心。但代码也是最少的。 在使用Lemuroid的时候,发现它不能检测…...
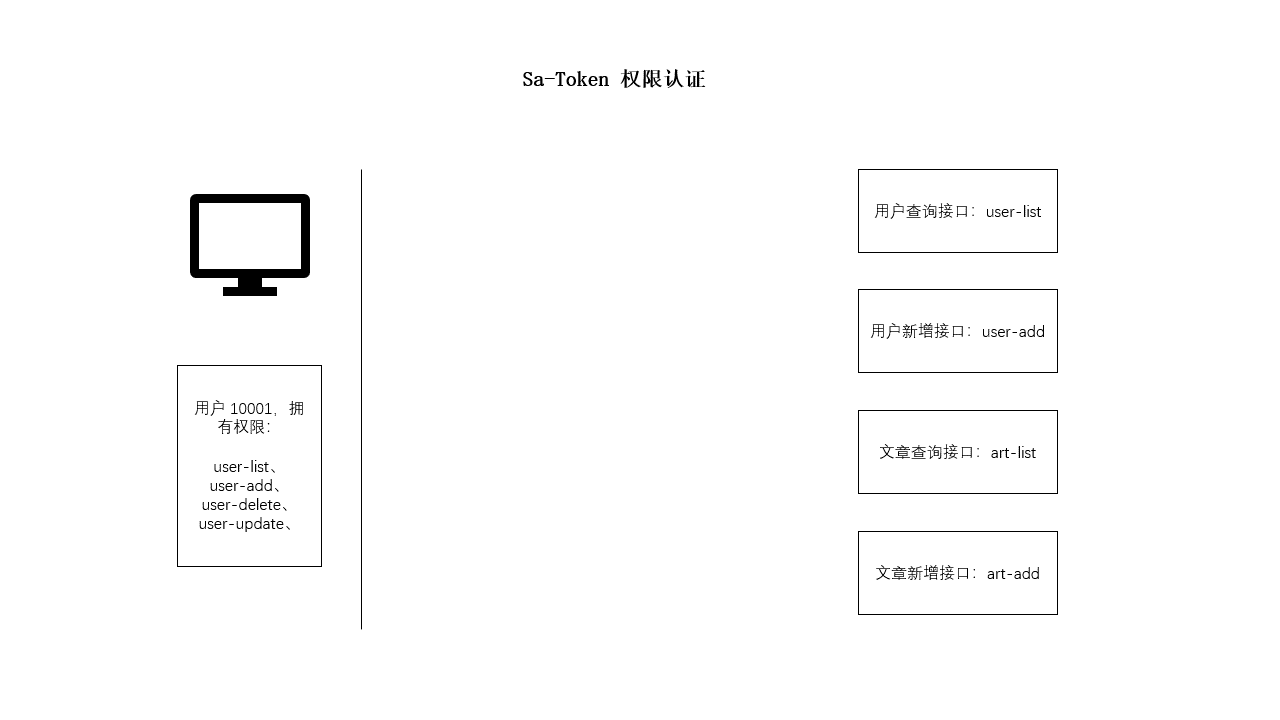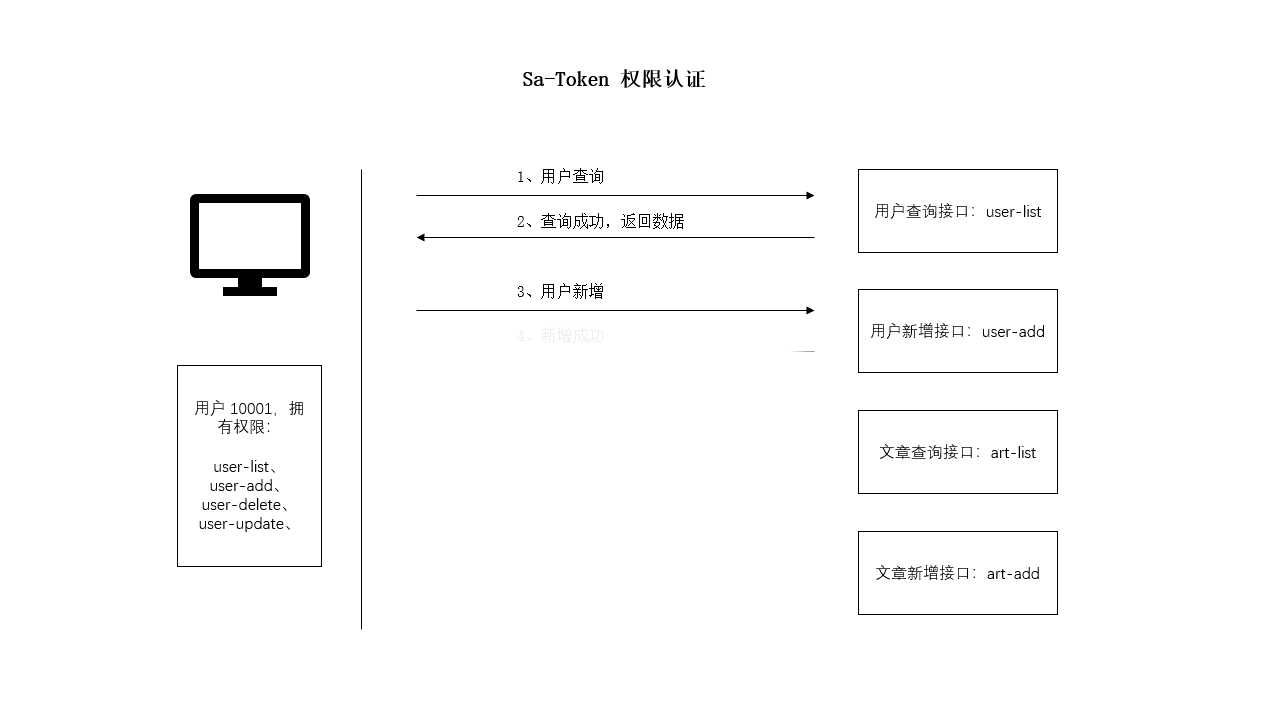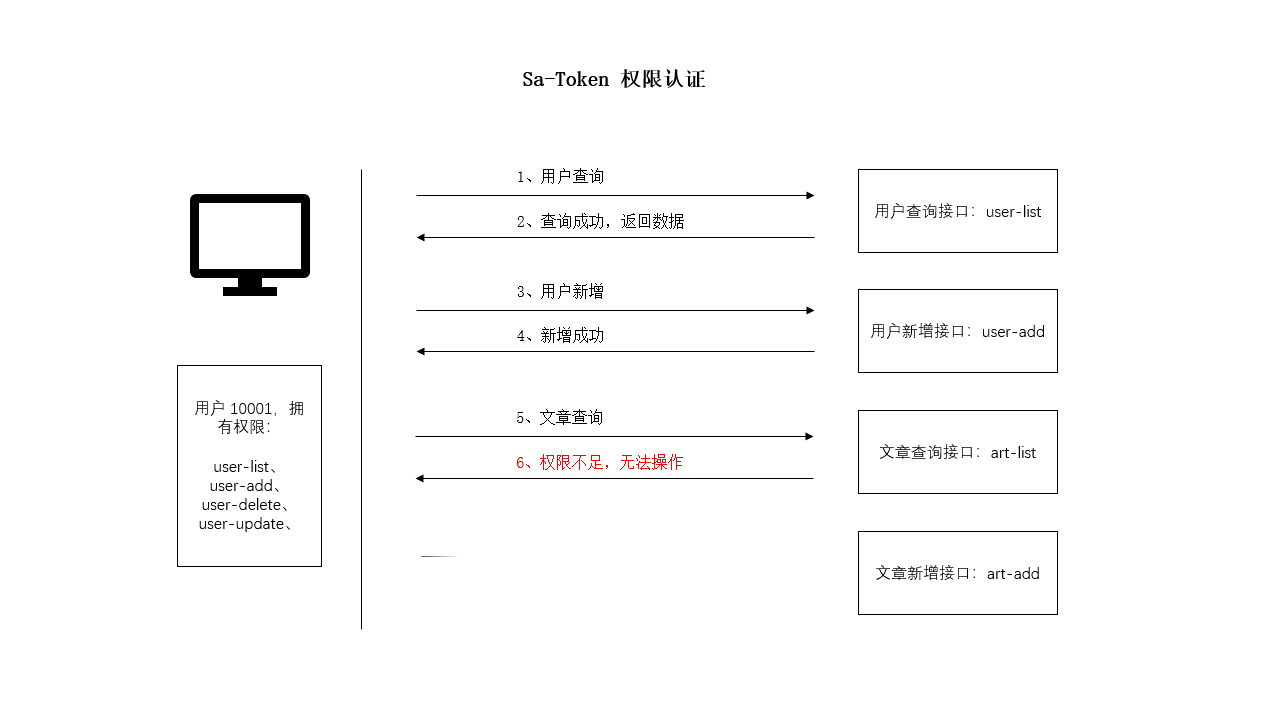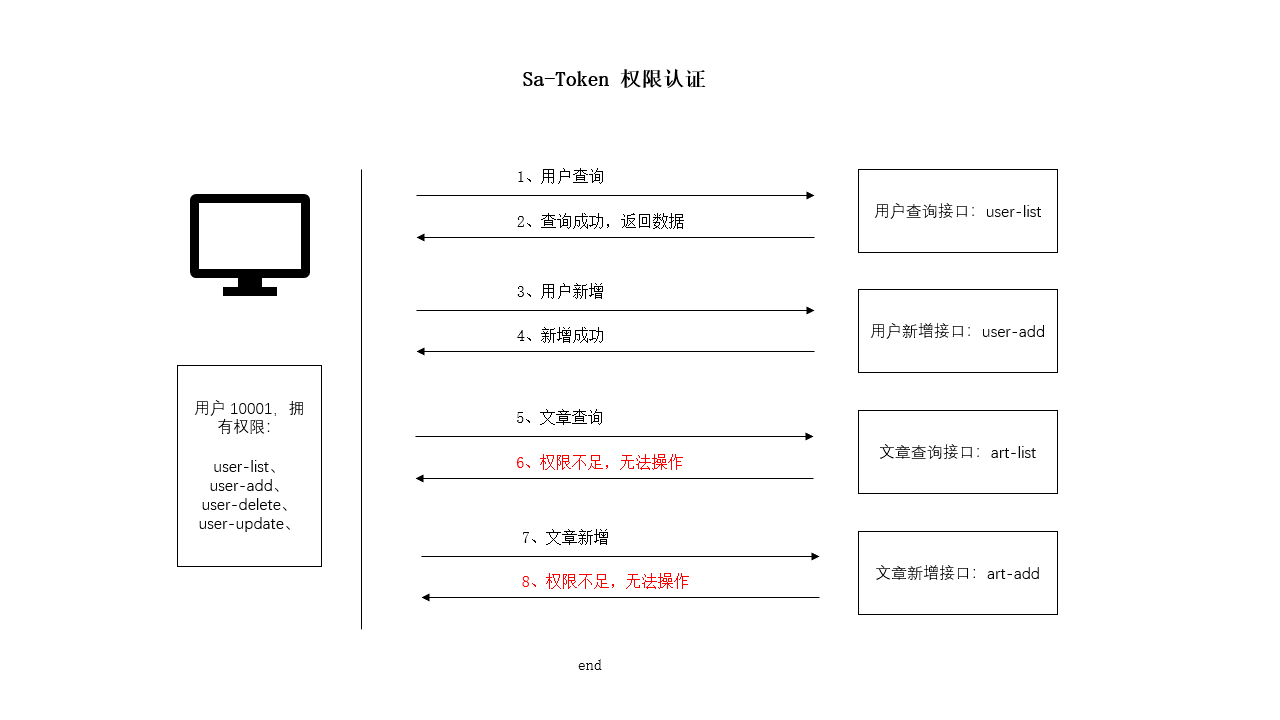
SpringBoot 使用 Sa-Token 完成权限认证
一、设计思路 所谓权限认证,核心逻辑就是判断一个账号是否拥有指定权限: 有,就让你通过。没有?那么禁止访问! 深入到底层数据中,就是每个账号都会拥有一个权限码集合,框架来校验这个集合中是…...

Spring核心与设计思想、创建与使用
文章目录 一、Spring是什么二、为什么要学习框架三、IoC和DI(一)IoC1. 认识IoC2. Spring的核心功能 (二)DI 四、Spring项目的创建(一)使用 Maven 方式创建一个 Spring 项目 五、Spring项目的使用࿰…...

mysql 备份 还原
1:备份 执行命令方案1: /usr/local/mysql/bin/mysqldump -uX -pX -h 127.0.0.1 --set-gtid-purgedOFF --skip-extended-insert --add-drop-table --add-locks --create-options --disable-keys --lock-tables --quick --set-charset -e --max_allowed_packet16777216 --net_b…...

每日学术速递4.26
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.AutoNeRF: Training Implicit Scene Representations with Autonomous Agents 标题:AutoNeRF:使用自主代理训练隐式场景表示 作者:Pierre Marz…...

RabbitMQ使用StringRedisTemplate-防止重复消费
造成重复消费的原因: MQ向消费者推送message,消费者向MQ返回ack,告知所推送的消息消费成功。但是由于网络波动等原因,可能造成消费者向MQ返回的ack丢失。MQ长时间(一分钟)收不到ack,于是会向消…...

临沂大学张继群寄语
目录 寄语 1、不能有不良睹好 2、坚毅的个性和勤奋的品质 3、会存钱...

线程学习笔记
1:Thread 线程的生命周期控制 2:Runnable 可执行的任务和程序 3:Callable 执行程序后返回结果 4:Future 收集程序返回结果 5:Executor 线程池 6:ForkJoin 默认线程池 每个线程有工作队列 工作窃取 7:RunnableFuture FutureTask 实现 Runnable 和 Future 执…...

代码随想录算法训练营第四十二天|01背包问题,你该了解这些!、01背包问题,你该了解这些! 滚动数组 、416. 分割等和子集
文章目录 01背包问题,你该了解这些!01背包问题,你该了解这些! 滚动数组416. 分割等和子集 01背包问题,你该了解这些! 题目链接:代码随想录 二维数组解决0-1背包问题 解题思路: 1.dp…...

结构体指针、数组指针和结构体数组指针
结构体指针 首先让我们定义结构体: struct stu { char name[20]; long number; float score[4]; }; 再定义指向结构体类型变量的指针变量: struct stu *student; /*定义结构体类型指针*/ student malloc(sizeof(struct stu)); /*为指针变量分…...

项目架构一些注意点
考虑系统的 稳定性 一、微服务的稳定性 1、如何解决那些不稳定的因素/问题?也是常说的如何容错。 2、一个系统的高可用取决于它本身和其强依赖的组件的高可用 3、消除单点 保活机制 健康检查 注册中心如何保障稳定性 注册中心集群 微服务本身对注册信息的本地持…...
Forefront GPT-4免费版:开启无限畅聊时代,乐享人工智能快感,无限制“白嫖”,还能和N多角色一起聊天?赶紧注册,再过些时间估计就要收费了
目录 前言注册登录方式应用体验聊天体验绘图体验 “是打算先免费后收费吗?”建议其它资料下载 前言 近期,人工智能技术迎来重大飞跃,OpenAI的ChatGPT等工具成为全球数亿人探索提高生产力和增强创造力的新方法。人们现在可以使用人工智能驱动…...
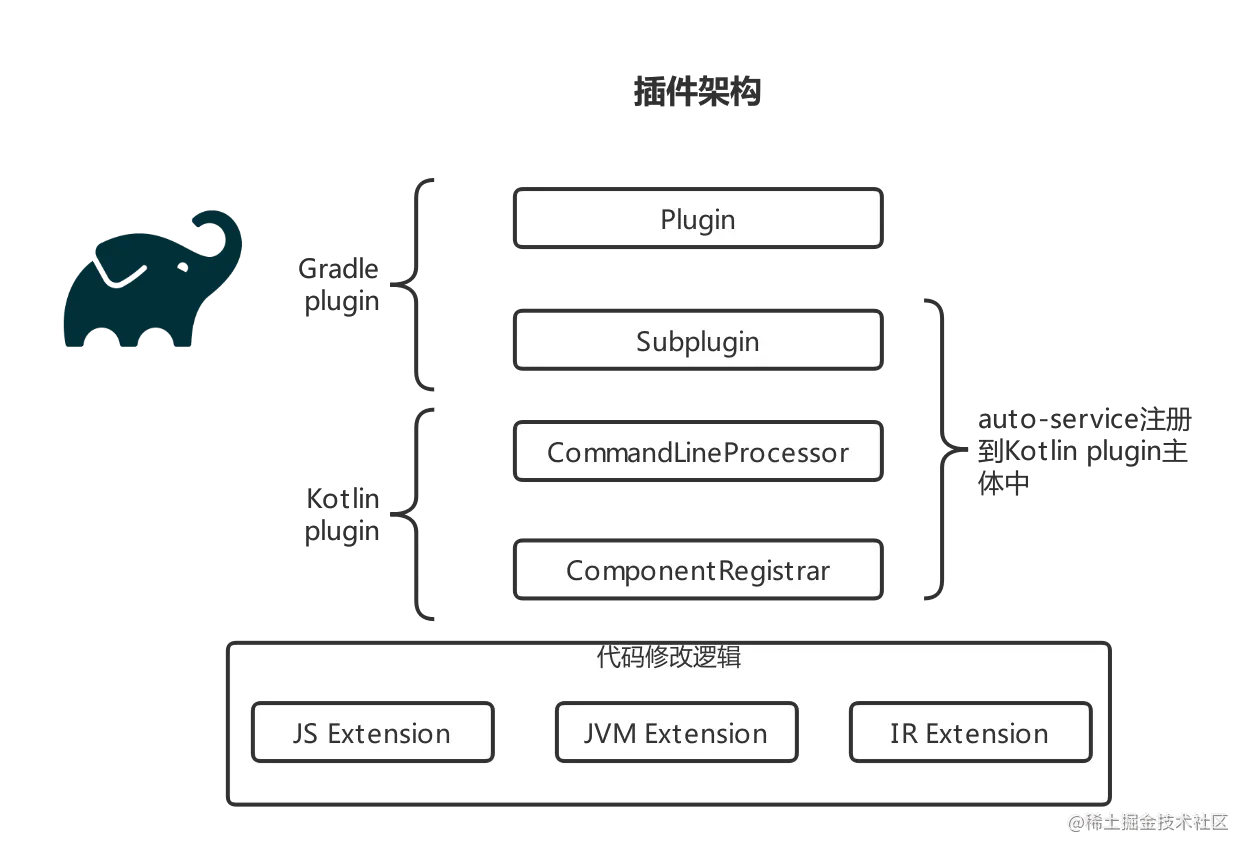
深入浅出 Compose Compiler(1) Kotlin Compiler KCP
前言 Compose 的语法简洁、代码效率非常高,这主要得益于 Compose Compiler 的一系列编译期魔法,帮开发者生成了很多样板代码。但编译期插桩也阻碍了我们对于 Compose 运行原理的认知,想要真正读懂 Compose 就必须先了解它的 Compiler。本系列…...
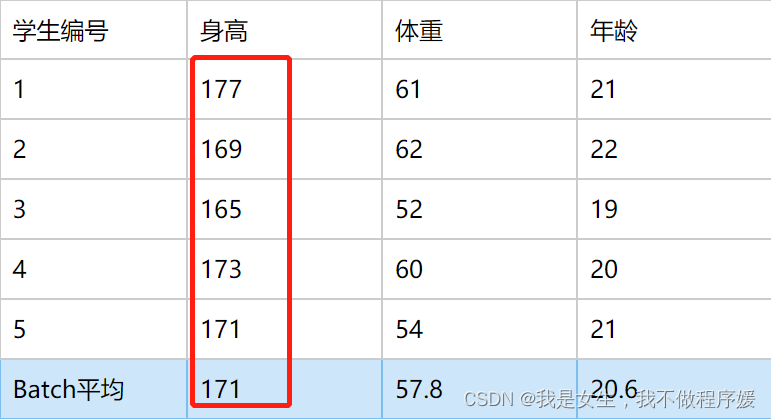
BatchNormalization和LayerNormalization的理解、适用范围、PyTorch代码示例
文章目录 为什么要NormalizationBatchNormLayerNormtorch代码示例 学习神经网络归一化时,文章形形色色,但没找到适合小白通俗易懂且全面的。学习过后,特此记录。 为什么要Normalization 当输入数据量级极大或极小时,为保证输出数…...

大数据 | 实验二:文档倒排索引算法实现
文章目录 📚实验目的📚实验平台📚实验内容🐇在本地编写程序和调试🥕代码框架思路🥕代码实现 🐇在集群上提交作业并执行🥕在集群上提交作业并执行,同本地执行相比即需修改…...

Java文档注释-JavaDoc标签
标签含义author指定作者{code}使用代码字体以原样显示信息,不处理HTML样式deprecated指定程序元素已经过时{docRoot}指定当前文档的根目录路径exception标识由方法或构造函数抛出的异常{inheritDoc}从直接超类中继承注释{link}插入指向另外一个主题的内联链接{linkp…...

黑盒测试过程中【测试方法】详解5-输入域,输出域,猜错法
在黑盒测试过程中,有9种常用的方法:1.等价类划分 2.边界值分析 3.判定表法 4.正交实验法 5.流程图分析 6.因果图法 7.输入域覆盖法 8.输出域覆盖法 9.猜错法 黑盒测试过程中【测试方法】讲解1-等价类,边界值,判定表_朝一…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
