代码随想录算法训练营第四十二天|01背包问题,你该了解这些!、01背包问题,你该了解这些! 滚动数组 、416. 分割等和子集
文章目录
- 01背包问题,你该了解这些!
- 01背包问题,你该了解这些! 滚动数组
- 416. 分割等和子集
01背包问题,你该了解这些!
- 题目链接:代码随想录
二维数组解决0-1背包问题
-
解题思路:
1.dp[i]|[j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式:不放物品i,放物品i dp[i]|[j] = max(dp[i - 1]|[j], dp[i - 1]|[j - weight[i]] + value[i]);
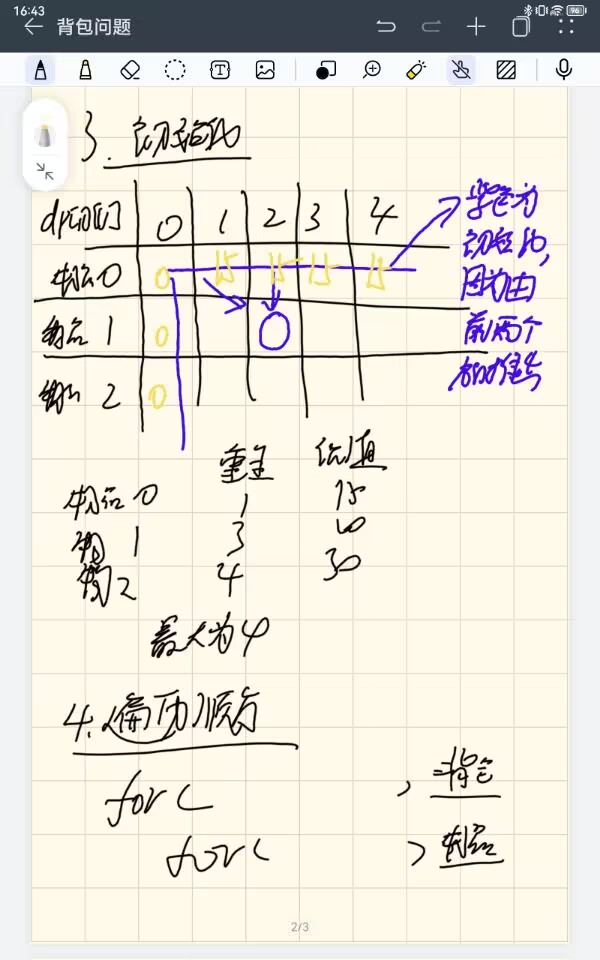
3.初始化;当前处理的结果都是由左上角推出来的,所以只用初始化左上和即可,即第一行和第一列
4.确定遍历顺序:本题无论是先遍历背包还是先遍历物品都可以 -
图像理解
public class BagProblem {public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){//1.创建dp数组//dp[i][j] 表示从0-i个物品中挑选物品,放入容量为j的背包中,所取得的最大价值int length = weight.length;int[][] dp = new int[length][bagSize + 1];//2.初始化数据,只初始化第一行,第一列默认初始化为0for (int i = weight[0]; i < dp.length; i++) {//i为物品0的重量dp[0][i] = value[0];}//3.遍历dp数组for (int i = 1; i < weight.length; i++) {for (int j = 1; j < bagSize + 1; j++) {if(j < weight[i]){/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i-1][j];}else{/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}for (int i = 0; i < length; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}
}
01背包问题,你该了解这些! 滚动数组
- 题目链接:代码随想录
一维数组解0-1背包问题
-
每次放入一个物品之后,求得的dp数组就是能放下一个物品的容量的最大价值
因此不用太考虑放入一个物品后前后容量关系,就考虑一个个将物品完全放入背包即可
-
解题思路:
1.dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
2.dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3.dp数组初始化的时候,都初始为0。这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了
4.先遍历放入物品,再遍历不同容量的背包,从后向前遍历 -
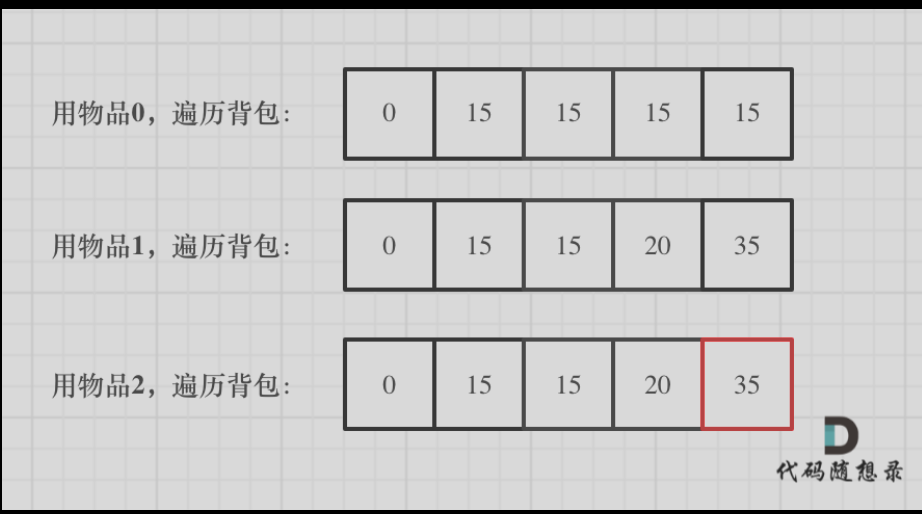
图像理解:
开始向背包里放的时候
public class BagProblemOneArray{public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;testWeightBagProblem(weight, value, bagWight);}public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){// int wLen = weight.length;// //定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值// int[] dp = new int[bagWeight + 1];// //遍历顺序:先遍历物品,再遍历背包容量// for (int i = 0; i < wLen; i++){// for (int j = bagWeight; j >= weight[i]; j--){// dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);// }// }// //打印dp数组// for (int j = 0; j <= bagWeight; j++){// System.out.print(dp[j] + " ");// }int goodsLength = weight.length;//背包的个数int[] dp = new int[bagWeight + 1];//dp数组for (int i = 0; i < goodsLength; i++) {for (int j = bagWeight; j >= weight[i]; j--) {dp[j] = Math.max(dp[j],dp[j - weight[i]] + value[i]);}}for (int i = 0; i <= bagWeight; i++) {System.out.print(dp[i] + " ");}}
}
416. 分割等和子集
- 题目链接代码随想录
本题因为元素只能用一次,因此是0-1背包问题
整体思路,找到元素价值量能恰好装进符合价值sum/2的容量的背包
本题每个商品价值量 = 重量
-
解题思路:
- dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了 - 递推公式:背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
- 初始化:dp数组都初始化为0
- 从后向前
- dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
-
图像理解:

public boolean canPartition(int[] nums) {//dp数组// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了 int[] dp = new int[10001];int sum = 0;//计算总和for (int i = 0; i < nums.length; i++) {sum += nums[i];}if(sum % 2 == 1){return false;}//为奇数,分成两个集合,必不成立int target = sum / 2;//0-1背包for (int i = 0; i < nums.length; i++) {for (int j = target; j >= nums[i];j--) {//j从target开始,因为背包目标重量为即最后求解的结果dp[j] = Math.max(dp[j],dp[j - nums[i] + nums[i]]);}}if(dp[target] == target){return true;}return false;
}
相关文章:

代码随想录算法训练营第四十二天|01背包问题,你该了解这些!、01背包问题,你该了解这些! 滚动数组 、416. 分割等和子集
文章目录 01背包问题,你该了解这些!01背包问题,你该了解这些! 滚动数组416. 分割等和子集 01背包问题,你该了解这些! 题目链接:代码随想录 二维数组解决0-1背包问题 解题思路: 1.dp…...

结构体指针、数组指针和结构体数组指针
结构体指针 首先让我们定义结构体: struct stu { char name[20]; long number; float score[4]; }; 再定义指向结构体类型变量的指针变量: struct stu *student; /*定义结构体类型指针*/ student malloc(sizeof(struct stu)); /*为指针变量分…...

项目架构一些注意点
考虑系统的 稳定性 一、微服务的稳定性 1、如何解决那些不稳定的因素/问题?也是常说的如何容错。 2、一个系统的高可用取决于它本身和其强依赖的组件的高可用 3、消除单点 保活机制 健康检查 注册中心如何保障稳定性 注册中心集群 微服务本身对注册信息的本地持…...
Forefront GPT-4免费版:开启无限畅聊时代,乐享人工智能快感,无限制“白嫖”,还能和N多角色一起聊天?赶紧注册,再过些时间估计就要收费了
目录 前言注册登录方式应用体验聊天体验绘图体验 “是打算先免费后收费吗?”建议其它资料下载 前言 近期,人工智能技术迎来重大飞跃,OpenAI的ChatGPT等工具成为全球数亿人探索提高生产力和增强创造力的新方法。人们现在可以使用人工智能驱动…...
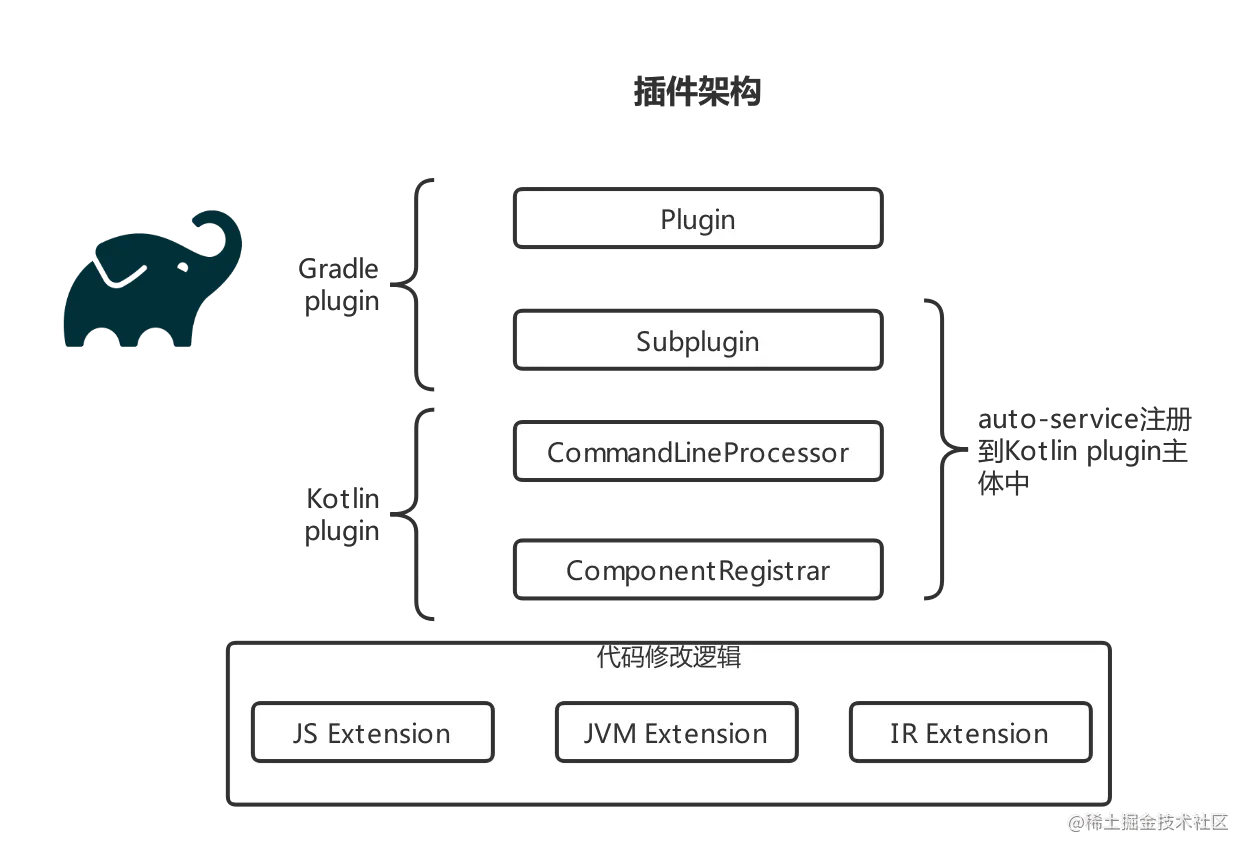
深入浅出 Compose Compiler(1) Kotlin Compiler KCP
前言 Compose 的语法简洁、代码效率非常高,这主要得益于 Compose Compiler 的一系列编译期魔法,帮开发者生成了很多样板代码。但编译期插桩也阻碍了我们对于 Compose 运行原理的认知,想要真正读懂 Compose 就必须先了解它的 Compiler。本系列…...
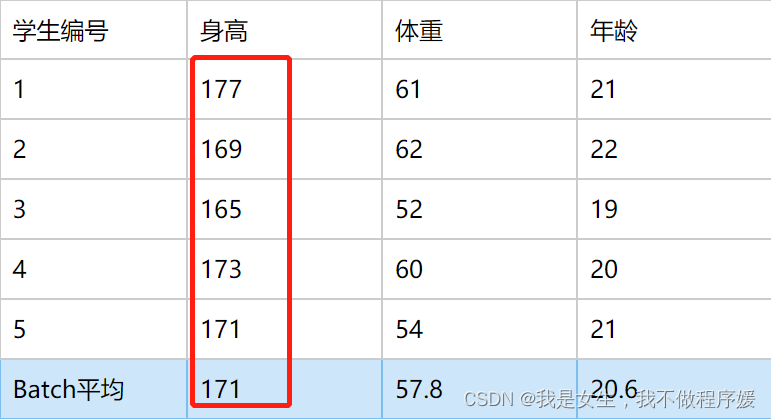
BatchNormalization和LayerNormalization的理解、适用范围、PyTorch代码示例
文章目录 为什么要NormalizationBatchNormLayerNormtorch代码示例 学习神经网络归一化时,文章形形色色,但没找到适合小白通俗易懂且全面的。学习过后,特此记录。 为什么要Normalization 当输入数据量级极大或极小时,为保证输出数…...

大数据 | 实验二:文档倒排索引算法实现
文章目录 📚实验目的📚实验平台📚实验内容🐇在本地编写程序和调试🥕代码框架思路🥕代码实现 🐇在集群上提交作业并执行🥕在集群上提交作业并执行,同本地执行相比即需修改…...

Java文档注释-JavaDoc标签
标签含义author指定作者{code}使用代码字体以原样显示信息,不处理HTML样式deprecated指定程序元素已经过时{docRoot}指定当前文档的根目录路径exception标识由方法或构造函数抛出的异常{inheritDoc}从直接超类中继承注释{link}插入指向另外一个主题的内联链接{linkp…...

黑盒测试过程中【测试方法】详解5-输入域,输出域,猜错法
在黑盒测试过程中,有9种常用的方法:1.等价类划分 2.边界值分析 3.判定表法 4.正交实验法 5.流程图分析 6.因果图法 7.输入域覆盖法 8.输出域覆盖法 9.猜错法 黑盒测试过程中【测试方法】讲解1-等价类,边界值,判定表_朝一…...
在Python中的使用)
Python学习之sh(shell脚本)在Python中的使用
文章目录 前言一、sh是什么?二、使用步骤1.安装2.使用示例3.使用sh执行命令4.关键字参数5.查找命令6.Baking参数 前言 本文章向大家介绍[Python库]分析一个python库–sh(系统调用),主要内容包括其使用实例、应用技巧、基本知识点…...

追求卓越:编写高质量代码的方法和技巧
本文讨论了编写高质量代码的重要性,并详细介绍了高质量代码的特征、编程实践技巧和软件工程方法论。通过遵循这些原则和实践,程序员可以编写出更稳定、可维护和可扩展的代码。 一、 前言 写出高质量代码是每个程序员的追求和目标。高质量的代码可以使程…...
(最终篇))
MATLAB算法实战应用案例精讲-【人工智能】机器视觉(概念篇)(最终篇)
目录 前言 几个高频面试题目 如何评价一个光源的好坏? 如何依靠光源增强图像对比度?...
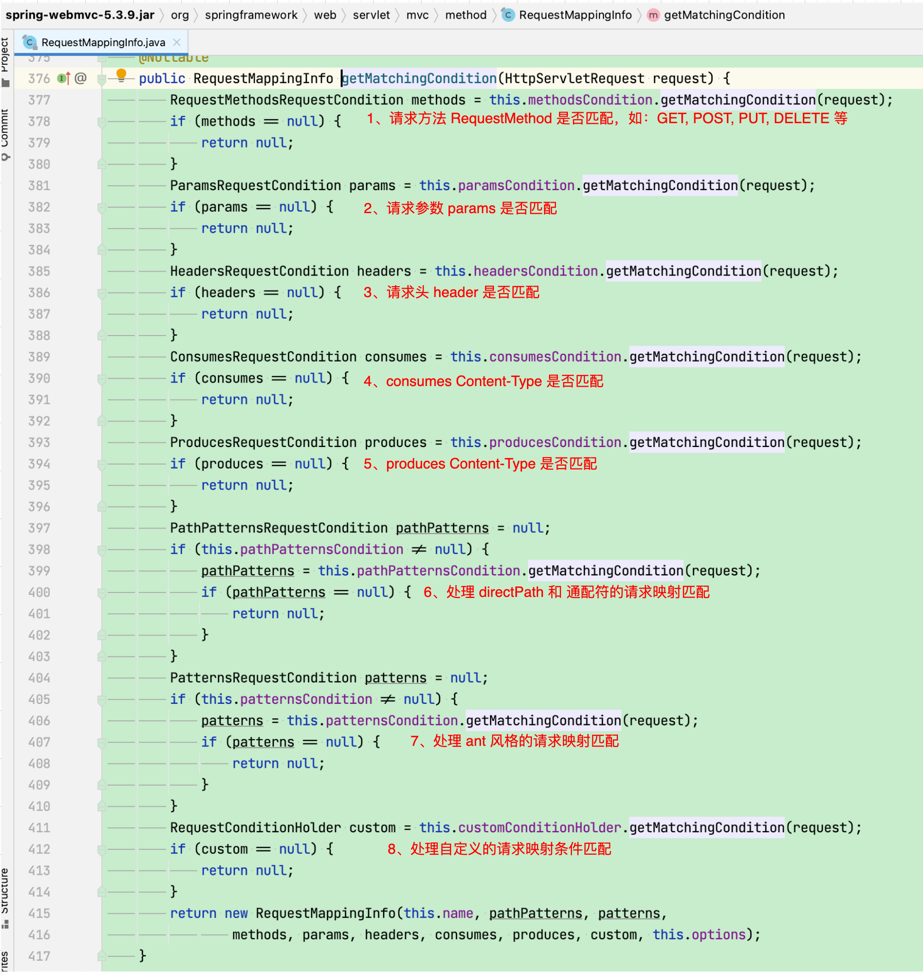
【老王读SpringMVC-3】根据 url 是如何找到 controller method 的?
前面分析了 request 与 handler method 映射关系的注册,现在再来分析一下 SpringMVC 是如何根据 request 来获取对应的 handler method 的? 可能有人会说,既然已经将 request 与 handler method 映射关系注册保存在了 AbstractHandlerMethodMapping.Ma…...
人机交互到艺术设计及玫瑰花绘制实例
Python库之图形用户界面 Riverbank Computing | Introduction Welcome to wxPython! | wxPython Overview — PyGObject Python库之游戏开发 https://www.pygame.org/news Panda3D | Open Source Framework for 3D Rendering & Games python.cocos2d.org Python库之…...

多臂老虎机问题
1.问题简介 多臂老虎机问题可以被看作简化版的强化学习问题,算是最简单的“和环境交互中的学习”的一种形式,不存在状态信息,只有动作和奖励。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都…...

DNS 查询原理详解
DNS(Domain Name System)是互联网上的一种命名系统,它将域名转换为IP地址。在进行DNS查询时,先要明确需要查询的主机名,然后向本地DNS服务器发出查询请求。 1. 本地DNS服务器查询 当用户在浏览器中输入一个URL或者点…...
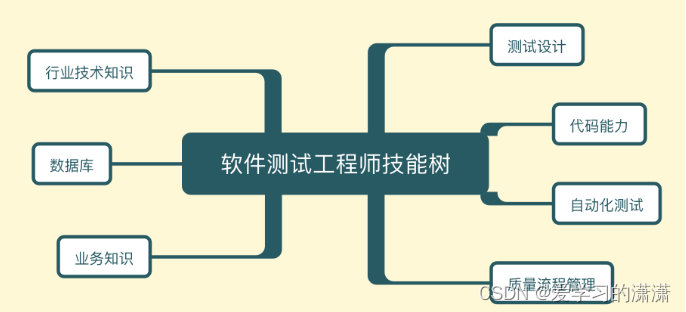
浅谈软件测试工程师的技能树
软件测试工程师是一个历史很悠久的职位,可以说从有软件开发这个行业以来,就开始有了软件测试工程师的角色。随着时代的发展,软件测试工程师的角色和职责也在悄然发生着变化,从一开始单纯的在瀑布式开发流程中担任测试阶段的执行者…...

转型产业互联网,新氧能否再造辉煌?
近年来,“颜值经济”推动医美行业快速发展,在利润驱动下,除了专注医美赛道的企业之外,也有不少第三方互联网平台正强势进入医美领域,使以新氧为代表的医美企业面对不小发展压力,同时也展现出强大的发展韧性…...
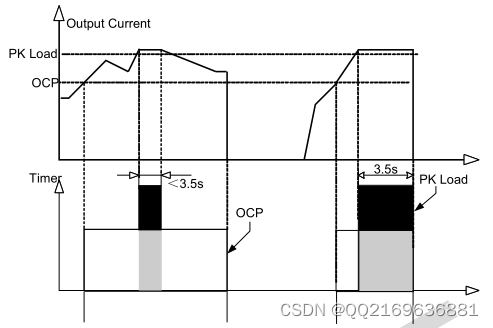
CRE66365 应用资料
CRE66365是一款高度集成的电流模式PWM控制IC,为高性能、低待机功耗和低成本的隔离型反激转换器。在正常负载条件下,AC输入高电压下工作在QR模式。为了最大限度地减少开关损耗,QR 模式下的最大开关频率被内部限制为 77kHz。当负载较低时&#…...
vue3快速上手学习笔记,还不快来看看?
Vue3快速上手 1.Vue3简介 2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王)耗时2年多、2600次提交、30个RFC、600次PR、99位贡献者github上的tags地址:https://github.com/vuejs/vue-next/release…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
