多臂老虎机问题
1.问题简介
多臂老虎机问题可以被看作简化版的强化学习问题,算是最简单的“和环境交互中的学习”的一种形式,不存在状态信息,只有动作和奖励。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都是一个特别经典的问题,理解它能够帮助我们学习强化学习。
2.问题介绍
2.1问题定义
在多臂老虎机(multi-armed bandit,MAB)问题中,有一个拥有 K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励的概率分布R。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励 。我们在各根拉杆的奖励概率分布未知的情况下,从头开始尝试,目标是在操作 T次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的,因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。

2.2形式化描述
多臂老虎机问题可以表示为一个元组,其中:
- A为动作集合,其中一个动作表示拉动一个拉杆。若多臂老虎机一共有K根拉杆,那动作空间就是集合
,我们用
表示任意一个动作;
- R为奖励概率分布,拉动每一根拉杆的动作a都对应一个奖励概率分布R(r|a),拉动不同拉杆的奖励分布通常是不同的。
假设每个时间步只能拉动一个拉杆,多臂老虎机的目标为最大化一段时间步T内累积的奖励:
其中表示在第t时间步拉动某一拉杆的动作,
表示动作
获得的奖励。
对于每一个动作a,定义其期望奖励为:
![]()
于是,至少存在一根拉杆,它的期望奖励不小于拉动其他任意一根拉杆,我们将该最优期望奖励表示为:
![]()
懊悔(regret)定义为拉动当前拉杆的动作a与最优拉杆的期望奖励差,即 :
累积懊悔(cumulative regret)即操作 T次拉杆后累积的懊悔总量,对于一次完整的T步决策,累积懊悔为 :
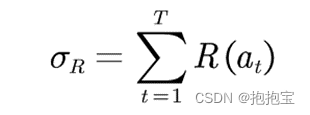
MAB 问题的目标为最大化累积奖励,等价于最小化累积懊悔。
为了知道拉动哪一根拉杆能获得更高的奖励,我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性,所以需要多次拉动一根拉杆,然后计算得到的多次奖励的期望,其算法流程如下所示:

以上 for 循环中的第四步如此更新估值,是因为这样可以进行增量式的期望更新,为什么不按照常规方法将所有数求和再除以次数呢?具体原因如下:
因为如果将所有数求和再除以次数,其缺点是每次更新的时间复杂度和空间复杂度均为 O(n)。而采用增量式更新,时间复杂度和空间复杂度均为O(1) 。
3. 代码实现
以下代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布(Bernoulli distribution),即每次拉下拉杆有P的概率获得的奖励为 1,有1-P的概率获得的奖励为 0。奖励为 1 代表获奖,奖励为 0 代表没有获奖。
# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as pltclass BernoulliBandit:""" 伯努利多臂老虎机,输入K表示拉杆个数 """def __init__(self, K):self.probs = np.random.uniform(size=K) # 随机生成K个0~1的数,作为拉动每根拉杆的获奖# 概率self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆self.best_prob = self.probs[self.best_idx] # 最大的获奖概率self.K = Kdef step(self, k):# 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1(获奖)或0(未# 获奖)if np.random.rand() < self.probs[k]:return 1else:return 0np.random.seed(1) # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %(bandit_10_arm.best_idx, bandit_10_arm.best_prob))接下来我们用一个 Solver 基础类来实现上述的多臂老虎机的求解方案。需要实现下列函数功能:根据策略选择动作、根据动作获取奖励、更新期望奖励估值、更新累积懊悔和计数。在下面的 MAB 算法基本框架中,我们将根据策略选择动作、根据动作获取奖励和更新期望奖励估值放在 run_one_step() 函数中,由每个继承 Solver 类的策略具体实现。而更新累积懊悔和计数则直接放在主循环 run() 中。
class Solver:""" 多臂老虎机算法基本框架 """def __init__(self, bandit):self.bandit = banditself.counts = np.zeros(self.bandit.K) # 每根拉杆的尝试次数self.regret = 0. # 当前步的累积懊悔self.actions = [] # 维护一个列表,记录每一步的动作self.regrets = [] # 维护一个列表,记录每一步的累积懊悔def update_regret(self, k):# 计算累积懊悔并保存,k为本次动作选择的拉杆的编号self.regret += self.bandit.best_prob - self.bandit.probs[k]self.regrets.append(self.regret)def run_one_step(self):# 返回当前动作选择哪一根拉杆,由每个具体的策略实现raise NotImplementedErrordef run(self, num_steps):# 运行一定次数,num_steps为总运行次数for _ in range(num_steps):k = self.run_one_step()self.counts[k] += 1self.actions.append(k)self.update_regret(k)相关文章:

多臂老虎机问题
1.问题简介 多臂老虎机问题可以被看作简化版的强化学习问题,算是最简单的“和环境交互中的学习”的一种形式,不存在状态信息,只有动作和奖励。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都…...

DNS 查询原理详解
DNS(Domain Name System)是互联网上的一种命名系统,它将域名转换为IP地址。在进行DNS查询时,先要明确需要查询的主机名,然后向本地DNS服务器发出查询请求。 1. 本地DNS服务器查询 当用户在浏览器中输入一个URL或者点…...
浅谈软件测试工程师的技能树
软件测试工程师是一个历史很悠久的职位,可以说从有软件开发这个行业以来,就开始有了软件测试工程师的角色。随着时代的发展,软件测试工程师的角色和职责也在悄然发生着变化,从一开始单纯的在瀑布式开发流程中担任测试阶段的执行者…...

转型产业互联网,新氧能否再造辉煌?
近年来,“颜值经济”推动医美行业快速发展,在利润驱动下,除了专注医美赛道的企业之外,也有不少第三方互联网平台正强势进入医美领域,使以新氧为代表的医美企业面对不小发展压力,同时也展现出强大的发展韧性…...
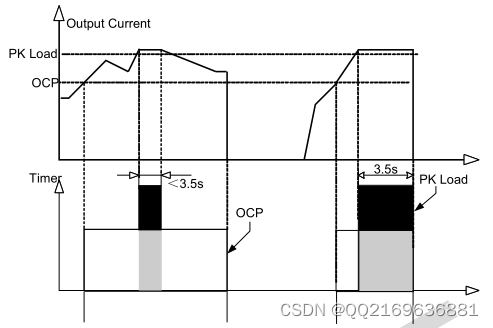
CRE66365 应用资料
CRE66365是一款高度集成的电流模式PWM控制IC,为高性能、低待机功耗和低成本的隔离型反激转换器。在正常负载条件下,AC输入高电压下工作在QR模式。为了最大限度地减少开关损耗,QR 模式下的最大开关频率被内部限制为 77kHz。当负载较低时&#…...
vue3快速上手学习笔记,还不快来看看?
Vue3快速上手 1.Vue3简介 2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王)耗时2年多、2600次提交、30个RFC、600次PR、99位贡献者github上的tags地址:https://github.com/vuejs/vue-next/release…...

HDU 5927 Auxiliary Set
原题链接: https://acm.hdu.edu.cn/showproblem.php?pid5927 题意: 有一颗根节点是1的树,其中有重要的点和不重要的点,重要的点需满足以下两个条件至少一个: 1.本来就是重要的点 2.是两个重要的点的最近共同祖先 有t…...

24:若所有参数皆需类型转换,请为此采用non-member函数
令class支持隐式类型转换通常是个糟糕的主意。 这条规则有其例外,最常见的例外是在建立数值类型时。 例,假设你设计一个class用来表现有理数,则允许整数“隐式转换”为有理数就很合理。 class Rational{ public:Rational(int numerator0,i…...
-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包)
CMake(2)-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包
目录 1.什么是CMake 1.1 编译流程CMakeLists.txt a) 最简单 demo1 b) 常用demo2 c) 单目录,源文件-输出文件 DIR_SRCS中 d)多目录,多源文件 1.2.执行命令: 1.3.自定义编译选项 2.安装和测试 3.支持GDB 4.添加环境检查 5.添加…...
)
java面试题(redis)
目录 1.redis主要消耗什么物理资源? 2.单线程为什么快 3.为什么要使用Redis 4.简述redis事务实现 5.redis缓存读写策略 6.redis除了做缓存,还能做些什么? 7.redis主从复制的原理 8.Redis有哪些数据结构?分别有哪些典型的应…...

Vue组件懒加载
组件懒加载 前言 组件懒加载最常用于异步加载大型/复杂组件或在需要时才进行加载 Vue 2和Vue 3均支持组件懒加载,本文将介绍如何在Vue 2和Vue 3中实现组件懒加载,和一些使用场景 1️⃣方法一:使用Webpack的代码分割能力 Vue 2和Vue 3都可以…...

Qt音视频开发42-网络推流(视频推流/本地摄像头推流/桌面推流/网络摄像头转发推流等)
一、前言 上次实现的文件推流,尽管优点很多,但是只能对现在存在的生成好的音视频文件推流,而现在更多的场景是需要将实时的视频流重新推流分发,用户在很多设备比如手机/平板/网页/电脑/服务器上观看,这样就可以很方便…...

更简单的存取Bean方式-@Bean方法注解
1.Bean方法存储 类注解是添加在某个类上的,那么方法注解是添加在某个方法前的 public class UserBeans {Beanpublic User user1(){User user new User();user.setUid(001);user.setUname("zhangsan");user.setAge(19);user.setPassword("123123");retur…...

边缘计算与AI布署应用电力物联网解决方案-RK3588开发平台
电力行业拥有规模庞大的各类设备,如电表、各类保护、采集、控制设备。面对分布式发电、储能、用户微网等一系列综合问题,边缘计算与AI布署可满足“端侧本地化”高效运用的需求,协助提升最后一公里运行效率。 瑞芯微RK3588J、内置独立NPU&…...

centos部署unity accelerator
参考 https://docs.unity3d.com/Manual/UnityAccelerator.html 方案1:下载Unity Accelerator 手动安装, unity-accelerator-app-v1.0.941g6b39b61.AppImage为下载的文件 1、放入服务器目录, chmod x unity-accelerator-app-v1.0.941g6b39b61.AppImage 2…...

HANA开发指南
建模方面 1、建模方式:图像化建模、SQL建模、CE语言建模 2、维护:SQL和CE比图形化建模更容易维护和修改 3、性能:图形化和CE会经过系统优化,性能一般优于SQL语言 4、可按需要设置参数、变量、Hierachy、聚合类型等 5、在S4系…...
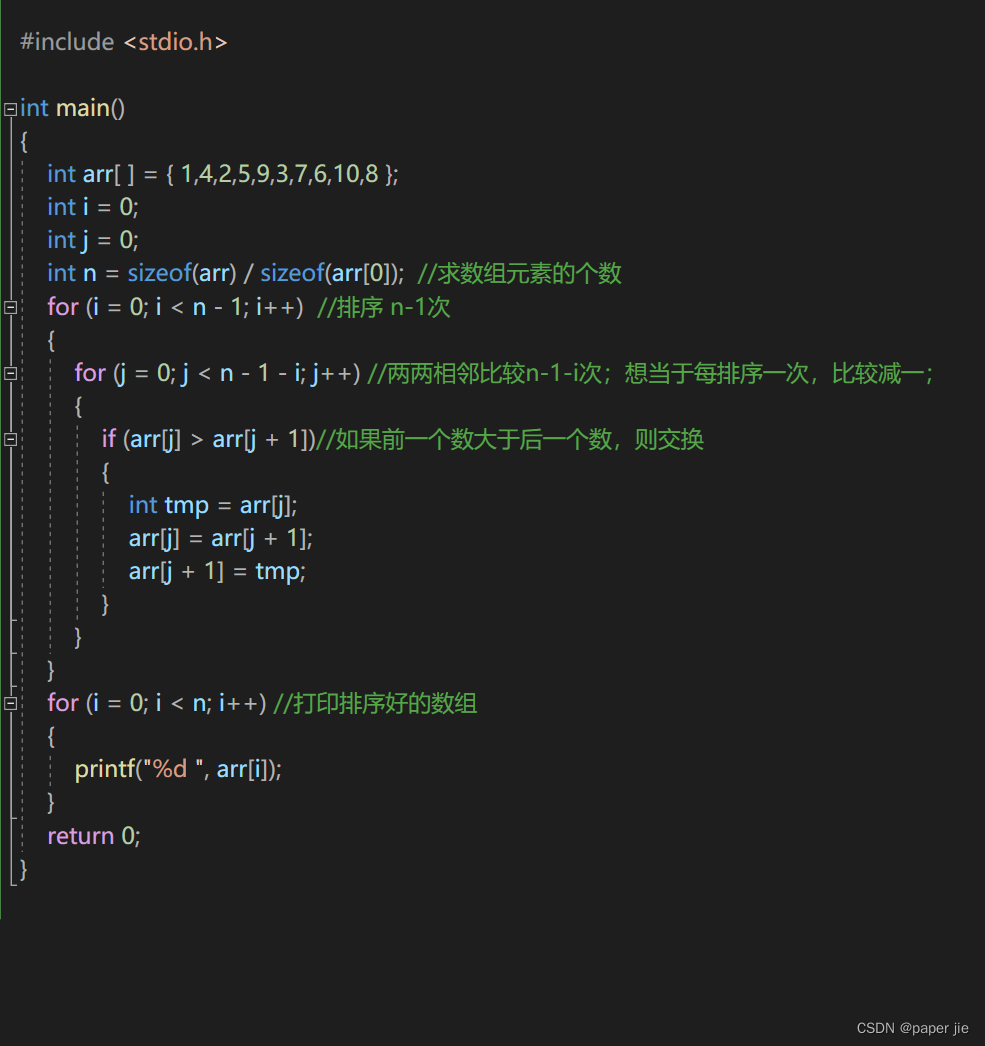
请问你见过吐代码的泡泡吗(冒泡排序)
🤩本文作者:大家好,我是paperjie,感谢你阅读本文,欢迎一建三连哦。 🥰内容专栏:这里是《算法详解》,笔者用重金(时间和精力)打造,将算法知识一网打尽,希望可以…...
【VM服务管家】VM4.0平台SDK_2.1环境配置类
目录 2.1.1 环境配置:CSharp二次开发环境配置方法2.1.2 环境配置:Qt二次开发环境配置方法2.1.3 环境配置:MFC二次开发环境配置方法2.1.4 环境配置:VB.Net二次开发环境配置方法2.1.5 环境配置:运行出现Vm.Core.Solution…...
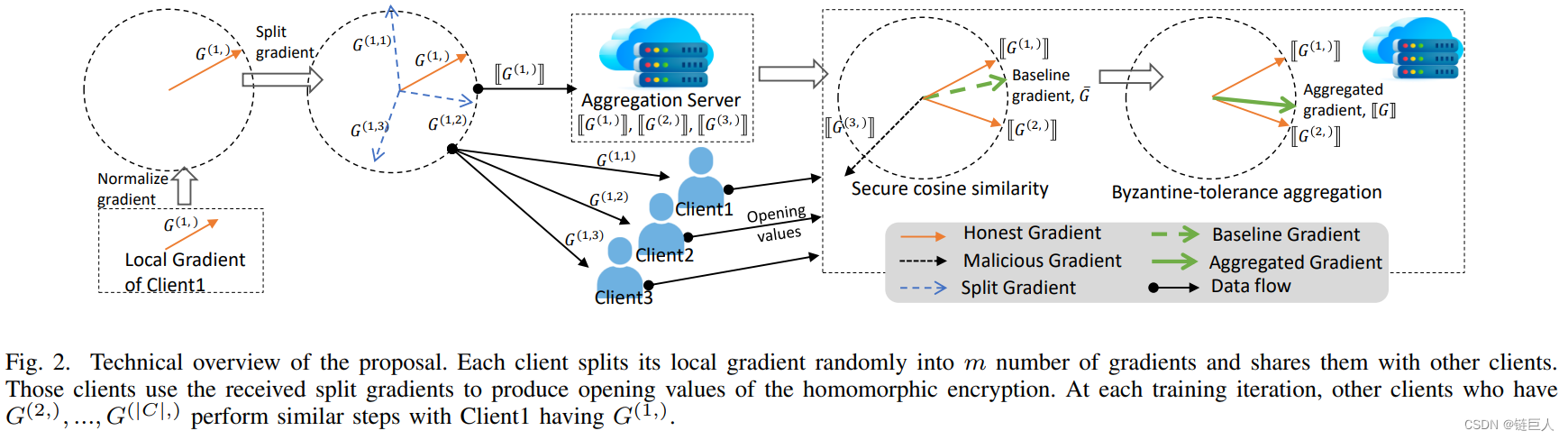
最新研究:可审计的具有拜占庭鲁棒的联邦学习方案
Y. Liang, Y. Li and B. -S. Shin, “Auditable Federated Learning With Byzantine Robustness,” in IEEE Transactions on Computational Social Systems, doi: 10.1109/TCSS.2023.3266019. 可免费下载:https://download.csdn.net/download/liangyihuai/87727720…...

JDK1.8下载、安装和环境配置教程
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🦾🦾 目录 window系统安装java 下载JDK 配置环境变量 …...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
