HDU 5927 Auxiliary Set
原题链接:
https://acm.hdu.edu.cn/showproblem.php?pid=5927
题意:
有一颗根节点是1的树,其中有重要的点和不重要的点,重要的点需满足以下两个条件至少一个:
1.本来就是重要的点
2.是两个重要的点的最近共同祖先
有t个测试实例,对于每个测试实例:
给出结点个数n和询问次数q
对于每次询问:
给出一个数con,表示不重要的点的个数
接下来con个数是不重要的点的编号
对于每个询问,求出重要的点的个数(每次询问之间相互独立)
思路:
ans记录重要结点的个数
本来就是重要的点有n-con个
那么我们就需要检查一下不重要的点,对于每个不重要的点看看他是不是两个重要的点的最近共同祖先
对于点u,如果他的以儿子结点为根的子树中,多于两个子树里有
重要的结点,那么u就能变成重要的结点
那么我们可以先预处理好每个结点的儿子结点的个数,每个点的父节点和每个点的深度
然后再对不重要的结点按照深度从大到小的顺序排序
从最深的结点u开始遍历,如果u的有重要点的儿子结点数量超过两个,那么u就可以变成重要结点,ans++
如果变不了重要结点,说明u的有重要点的儿子结点数量要么是0要么是1,如果是0,那么u的父节点的有重要儿子结点的数量就需要-1,因为每次询问独立,那么我们需要将减掉的点给记录一下,当这次询问完毕时再复原加上
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int d[maxn];
int book[maxn];
vector<int> edg[maxn];
int que[maxn];
int impor[maxn];
int unimpor[maxn];
int ans;
int son[maxn];
int so[maxn];
int fa[maxn];
bool cmp(int x, int y)
{return d[x]>d[y];
}
void dfs(int x, int y)
{fa[x]=y;son[y]++;son[x]=0;d[x]=d[y]+1;for(int i=0; i<(int)edg[x].size(); i++){if(edg[x][i]!=y)dfs(edg[x][i],x);}return;
}
int main()
{int t;cin>>t;int e=1; while(t--){int n;int q;scanf("%d%d", &n, &q);int i, j, x, y;for(i=0; i<n-1; i++){scanf("%d %d", &x, &y);edg[x].push_back(y);edg[y].push_back(x); }dfs(1,0);int m;printf("Case #%d:\n", e++); while(q--){scanf("%d", &m);for(i=0; i<m; i++){ scanf("%d", &unimpor[i]);//不重要节点so[unimpor[i]]=son[unimpor[i]];//节点的儿子}ans=n-m;sort(unimpor, unimpor+m, cmp);for(i=0; i<m; i++){if(so[unimpor[i]]>=2)ans++;else{if(so[unimpor[i]]==0) so[fa[unimpor[i]]]--;}}printf("%d\n", ans);}for(i=1; i<=n; i++){edg[i].clear();
// vector<int>().swap(edg[i]);}}
}相关文章:

HDU 5927 Auxiliary Set
原题链接: https://acm.hdu.edu.cn/showproblem.php?pid5927 题意: 有一颗根节点是1的树,其中有重要的点和不重要的点,重要的点需满足以下两个条件至少一个: 1.本来就是重要的点 2.是两个重要的点的最近共同祖先 有t…...

24:若所有参数皆需类型转换,请为此采用non-member函数
令class支持隐式类型转换通常是个糟糕的主意。 这条规则有其例外,最常见的例外是在建立数值类型时。 例,假设你设计一个class用来表现有理数,则允许整数“隐式转换”为有理数就很合理。 class Rational{ public:Rational(int numerator0,i…...
-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包)
CMake(2)-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包
目录 1.什么是CMake 1.1 编译流程CMakeLists.txt a) 最简单 demo1 b) 常用demo2 c) 单目录,源文件-输出文件 DIR_SRCS中 d)多目录,多源文件 1.2.执行命令: 1.3.自定义编译选项 2.安装和测试 3.支持GDB 4.添加环境检查 5.添加…...
)
java面试题(redis)
目录 1.redis主要消耗什么物理资源? 2.单线程为什么快 3.为什么要使用Redis 4.简述redis事务实现 5.redis缓存读写策略 6.redis除了做缓存,还能做些什么? 7.redis主从复制的原理 8.Redis有哪些数据结构?分别有哪些典型的应…...

Vue组件懒加载
组件懒加载 前言 组件懒加载最常用于异步加载大型/复杂组件或在需要时才进行加载 Vue 2和Vue 3均支持组件懒加载,本文将介绍如何在Vue 2和Vue 3中实现组件懒加载,和一些使用场景 1️⃣方法一:使用Webpack的代码分割能力 Vue 2和Vue 3都可以…...

Qt音视频开发42-网络推流(视频推流/本地摄像头推流/桌面推流/网络摄像头转发推流等)
一、前言 上次实现的文件推流,尽管优点很多,但是只能对现在存在的生成好的音视频文件推流,而现在更多的场景是需要将实时的视频流重新推流分发,用户在很多设备比如手机/平板/网页/电脑/服务器上观看,这样就可以很方便…...

更简单的存取Bean方式-@Bean方法注解
1.Bean方法存储 类注解是添加在某个类上的,那么方法注解是添加在某个方法前的 public class UserBeans {Beanpublic User user1(){User user new User();user.setUid(001);user.setUname("zhangsan");user.setAge(19);user.setPassword("123123");retur…...

边缘计算与AI布署应用电力物联网解决方案-RK3588开发平台
电力行业拥有规模庞大的各类设备,如电表、各类保护、采集、控制设备。面对分布式发电、储能、用户微网等一系列综合问题,边缘计算与AI布署可满足“端侧本地化”高效运用的需求,协助提升最后一公里运行效率。 瑞芯微RK3588J、内置独立NPU&…...

centos部署unity accelerator
参考 https://docs.unity3d.com/Manual/UnityAccelerator.html 方案1:下载Unity Accelerator 手动安装, unity-accelerator-app-v1.0.941g6b39b61.AppImage为下载的文件 1、放入服务器目录, chmod x unity-accelerator-app-v1.0.941g6b39b61.AppImage 2…...

HANA开发指南
建模方面 1、建模方式:图像化建模、SQL建模、CE语言建模 2、维护:SQL和CE比图形化建模更容易维护和修改 3、性能:图形化和CE会经过系统优化,性能一般优于SQL语言 4、可按需要设置参数、变量、Hierachy、聚合类型等 5、在S4系…...
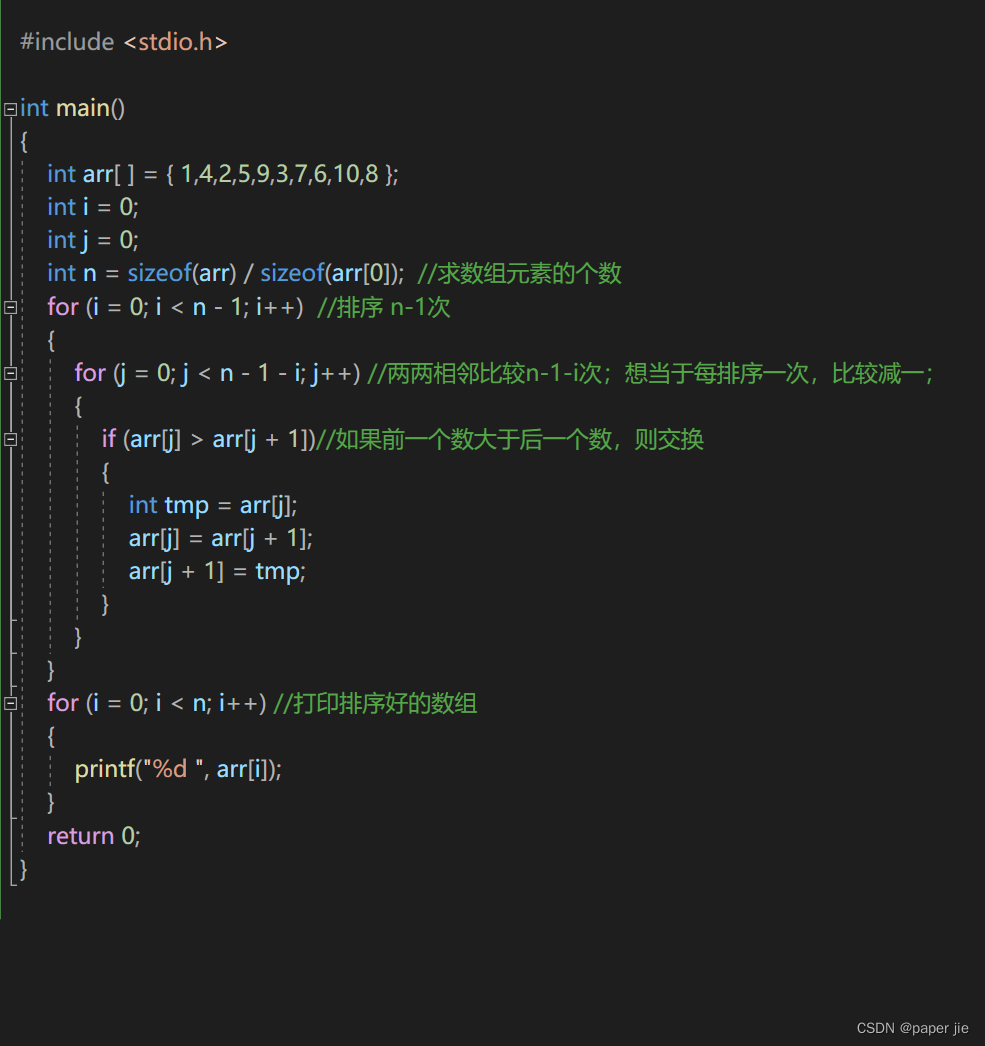
请问你见过吐代码的泡泡吗(冒泡排序)
🤩本文作者:大家好,我是paperjie,感谢你阅读本文,欢迎一建三连哦。 🥰内容专栏:这里是《算法详解》,笔者用重金(时间和精力)打造,将算法知识一网打尽,希望可以…...
【VM服务管家】VM4.0平台SDK_2.1环境配置类
目录 2.1.1 环境配置:CSharp二次开发环境配置方法2.1.2 环境配置:Qt二次开发环境配置方法2.1.3 环境配置:MFC二次开发环境配置方法2.1.4 环境配置:VB.Net二次开发环境配置方法2.1.5 环境配置:运行出现Vm.Core.Solution…...
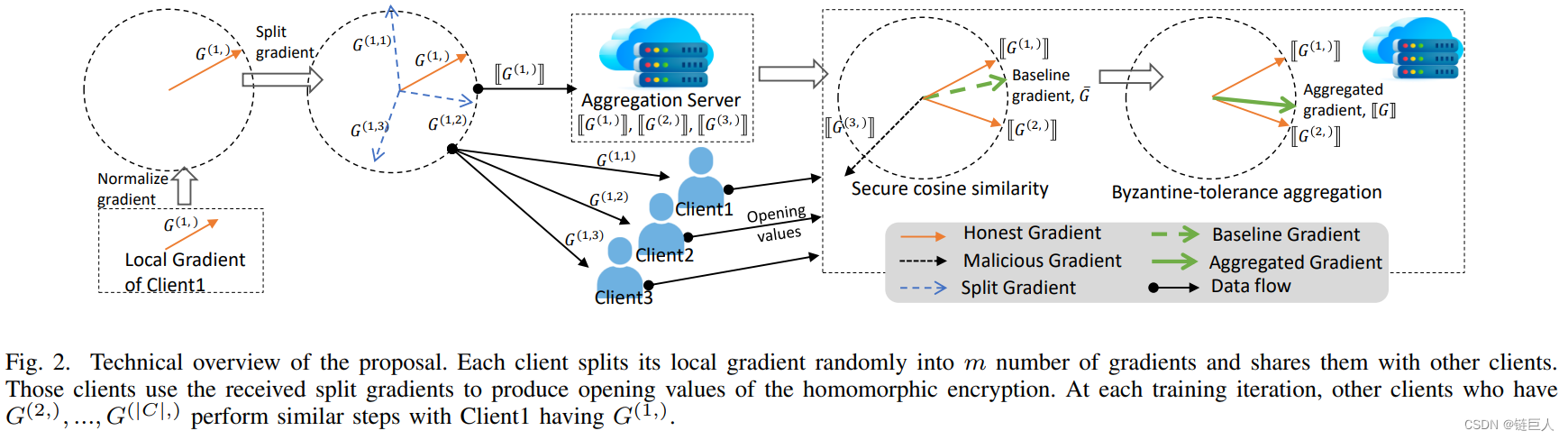
最新研究:可审计的具有拜占庭鲁棒的联邦学习方案
Y. Liang, Y. Li and B. -S. Shin, “Auditable Federated Learning With Byzantine Robustness,” in IEEE Transactions on Computational Social Systems, doi: 10.1109/TCSS.2023.3266019. 可免费下载:https://download.csdn.net/download/liangyihuai/87727720…...

JDK1.8下载、安装和环境配置教程
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🦾🦾 目录 window系统安装java 下载JDK 配置环境变量 …...

天津超算,青索帮助文档
连接 第一步,点击 配置VPN(切换到局域网用)和机器(也就是各套超算系统)。 第二步,点击 机器 选择对应的机器。通常会在下方显示可用的机器,单击其中一个即可。如果只有一个机器,…...

SpringMVC的拦截器和异常处理器
目录 lerInterceptor 拦截器 1、拦截器的作用 2、拦截器的创建 3、拦截器的三个抽象方法 4、拦截器的配置 5、多个拦截器的执行顺序 SpringMVC的异常处理器 1、异常处理器概述 2、基于配置文件的异常处理 3、基于注解的异常处理 lerInterceptor 拦截器 1、拦截器的作…...

查看库文件是32位还是64位|查看lib是静态库还是导入库|判断是debug模式还是release模式
文章目录 dll位数查看lib位数查看查看lib库是静态库还是导入库dll库文件信息查看lib库文件内容查看dll库查看编译模式是debug还是release方法一方法二方法三 lib静态库查看编译模式是debug还是release方法一方法二 lib导入库查看编译模式是debug还是release查看Linux下的.a库&a…...

Python小姿势 - Python爬取数据的库——Scrapy
Python爬取数据的库——Scrapy 一、爬虫的基本原理 爬虫的基本原理就是模拟人的行为,使用指定的工具和方法访问网站,然后把网站上的内容抓取到本地来。 爬虫的基本步骤: 1、获取URL地址: 2、发送请求获取网页源码; 3、…...

[C++初阶]栈和队列_优先级队列的模拟实现 deque类 的理解
为了更好的理解优先级队列priority_queue,这里会同时进行栈和队列的提及 文章目录 简要概念(栈和队列)栈和队列的模拟实现与使用stack(栈)deque的理解和操作queue priority_queue(优先级队列)框…...
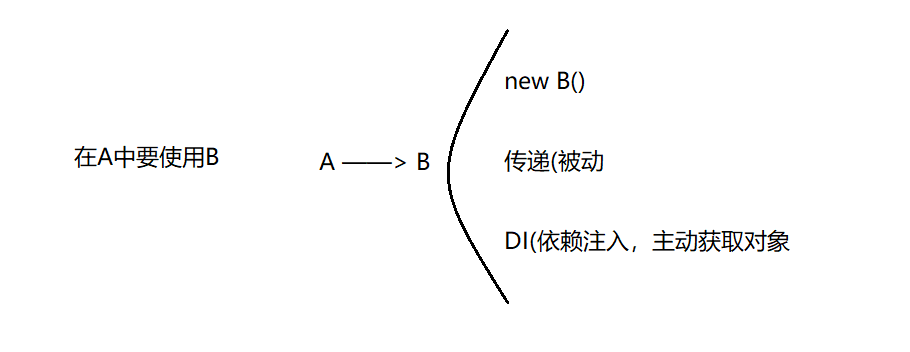
Spring是什么?关于Spring家族
初识Spring 什么是Spring? Spring是一个开源的Java企业级应用程序开发框架,由Rod Johnson于2003年创建,并在接下来的几年里得到了广泛的发展和应用。它提供了一系列面向对象的编程和配置模型,支持开发各种类型的应用程序&#x…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
