BM43-包含min函数的栈
题目
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的 min 函数,输入操作时保证 pop、top 和 min 函数操作时,栈中一定有元素。
此栈包含的方法有:
- push(value):将value压入栈中
- pop():弹出栈顶元素
- top():获取栈顶元素
- min():获取栈中最小元素
数据范围:操作数量满足 0≤n≤300,输入的元素满足 ∣val∣≤10000。
进阶:栈的各个操作的时间复杂度是 O(1),空间复杂度是 O(n)。
示例:
输入: ["PSH-1","PSH2","MIN","TOP","POP","PSH1","TOP","MIN"]
输出: -1,2,1,-1
解析:
- "PSH-1"表示将-1压入栈中,栈中元素为-1
- "PSH2"表示将2压入栈中,栈中元素为2,-1
- “MIN”表示获取此时栈中最小元素==>返回-1
- "TOP"表示获取栈顶元素==>返回2
- "POP"表示弹出栈顶元素,弹出2,栈中元素为-1
- "PSH1"表示将1压入栈中,栈中元素为1,-1
- "TOP"表示获取栈顶元素==>返回1
- “MIN”表示获取此时栈中最小元素==>返回-1
示例1
输入:["PSH-1","PSH2","MIN","TOP","POP","PSH1","TOP","MIN"]
返回值:-1,2,1,-1
思路:双栈实现
- element栈:具体存储元素。
- support栈:辅助栈,比较当前元素和此栈栈顶元素的值,取最小值放入此栈中,它就一直维护当前栈的最小值。
代码
import java.util.Stack;public class Solution { //具体存储元素private Stack<Integer> element = new Stack<>();//辅助栈,一直保存最小元素private Stack<Integer> support = new Stack<>();;public void push(int node) {element.push(node);if(support.isEmpty()) {support.push(node);} else {int tmpMin = support.peek();//比较当前元素和tmpMin谁更小,将最小元素push进辅助栈中int min = Math.min(node, tmpMin);support.push(min);}}public void pop() {element.pop();support.pop();}public int top() {return element.peek();}public int min() {return support.peek();}
}相关文章:

BM43-包含min函数的栈
题目 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的 min 函数,输入操作时保证 pop、top 和 min 函数操作时,栈中一定有元素。 此栈包含的方法有: push(value):将value压入栈中pop():弹出栈顶元素top():获取…...

[学习笔记] [机器学习] 3. KNN( K-近邻算法)及练习案例
视频链接数据集下载地址:《3. KNN及练习案例》配套数据集 1. K-近邻算法(KNN)概念 学习目标: 掌握K-近邻算法实现过程知道K-近邻算法的距离公式知道K-近邻算法的超参数 K K K值以及取值问题知道kd树实现搜索的过程应用KNeighborsClassifier实现分类知…...

React Hooks 钩子函数错误用法,你还在犯这些错误吗
React Hooks 常见错误 前言 本片文章主要是在写react hooks的时候,遇到的常见错误的写法,和错误。也是一个对只是的巩固和总结。 错误一 上代码:正确写法 function TestReactHooksError() {const [test, setTest] useState(test);useEff…...
)
tpm2-tools源码分析之tpm2_evictcontrol.c(1)
TPM 2.0中的tpm2_evictcontrol命令对应的源文件就是tpm2_evictcontrol.c,该文件位于tpm2-tools/tools/下,一共有339行(版本5.5)。 tpm2_evictcontrol的功能是使一个被加载的密钥持久保存、或者从TPM中移除一个持久密钥。命令描述…...

SpringCloud_OpenFeign服务调用和Resilience4J断路器
文章目录 一、负载均衡概论1、服务器负载均衡2、客户端负载均衡3、客户端负载均衡策略(SpringCloudRibbon)4、客户端负载均衡策略(SpringCloudLoadBalancer) 二、SpringCloudOpenFeign服务调用1、OpenFeign服务调用的使用2、OpenFeign服务调用的日志增强3、OpenFeign服务调用超…...

【C++】switch 语句
目录 1、缘起 2、笔记整理 3、if 和 switch 区别 4、总结 1、缘起 最近(2023-04-29)在 BiliBili 黑马程序员学习 C 编程语言,今天学习到了 switch 语句。以前在学习 C 语言 的时候,对这块知识点掌握的不是很好,…...

【Database-06】Centos 9 安装docker版的Oceanbase
1、安装docker 1.1、卸载旧版本 旧版本的 Docker 被称为docker或docker-engine。如果安装了这些,卸载它们以及相关的依赖项。 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...

TiDB Operator 和 Operator Dashboard
TiDB Operator 和 Operator Dashboard V1TiDB Operator概念实现 Operator Dashboard概念实现 V2思路实例代码TiDB ARM OperatorTiDB ARM Operator Dashboard V1 为了演示如何编写 TiDB Operator 和 Operator Dashboard,我们将分别介绍它们的概念和实现。 TiDB Ope…...
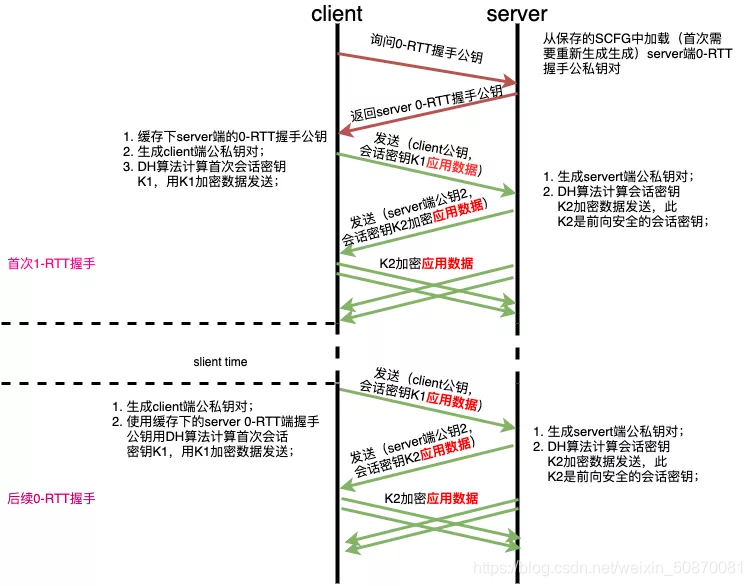
计算机网络闲谈01——QUIC协议
计算机网络闲谈01——QUIC协议 预备知识 重传机制 RTT 一个连接的往返时间 RTO 重传超时时间 RTT和RTO 的关系是:由于网络波动的不确定性,每个RTT都是动态变化的,所以RTO也应随着RTT动态变化。 流量控制 对发送方发送速率的控制 称之为…...

楼层滚动效果(超级简单,易懂)
系列文章目录 文章目录 系列文章目录一、楼层滚动效果图如下1. 下图是纯Css实现的楼层滚动2.通过Js优化后的楼层滚动如下图(🌹🌹) 二、楼层滚动(Css实现)1.滚动原理2.代码如下 三、楼层滚动(JsCss优化后的楼层滚动&…...
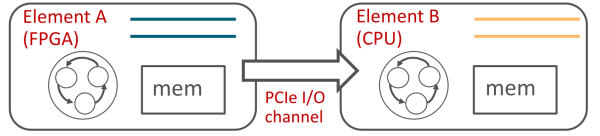
FPGA、 CPU、GPU、ASIC区别
一、为什么使用 FPGA? 众所周知,通用处理器(CPU)的摩尔定律已入暮年,而机器学习和 Web 服务的规模却在指数级增长。 人们使用定制硬件来加速常见的计算任务,然而日新月异的行业又要求这些定制的硬件可被重新…...

ChatGPT 之父承认 GPT-5 并不存在,为什么 OpenAI 总是这么实诚?|万字详述
ChatGPT 诞生前传 来源: 爱范儿 微信号:ifanr 最近,OpenAI 的 CEO Sam Altman 在一场公开会议上为 GPT-5 辟谣。 他声称 OpenAI 并没有在训练 GPT-5,而是一直基于 GPT-4 做别的工作。 OpenAI 是一家非常有趣的机构,和微软、Go…...
华为交换机配置telnet登录图文教程
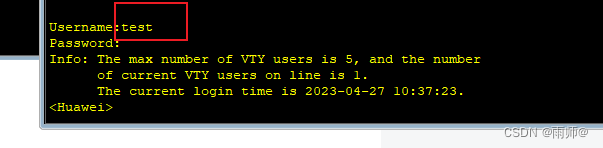
一、配置交换机管理vlan和地址,配置交换机接口 1.关闭多余的信息提示: [Huawei]undo in en Info: Information center is disabled. [Huawei] 2.交换机配置 在工作中通过Telnet方式登录交换机进行设备登录管理能更加便利,不需要到机房里…...
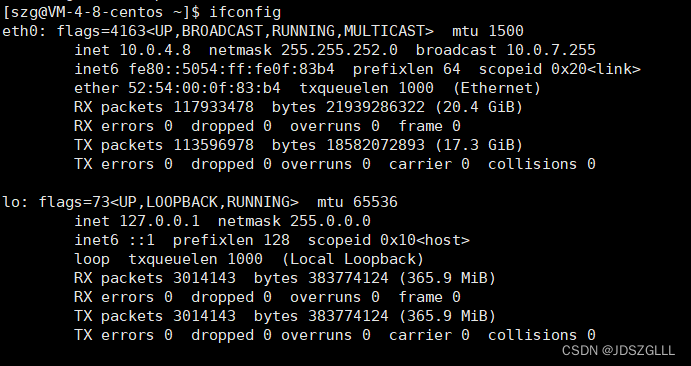
Linux:网络基础1
网络协议分层 所有网络问题,本质都是通信距离变长了,为了尽可能减少通信成本,定制了协议。 协议分层的优势: 软件设计方面的优势 - 低耦合 一般我们的分层依据: 功能比较集中,耦合度比较高的模块-- 一层 ,…...
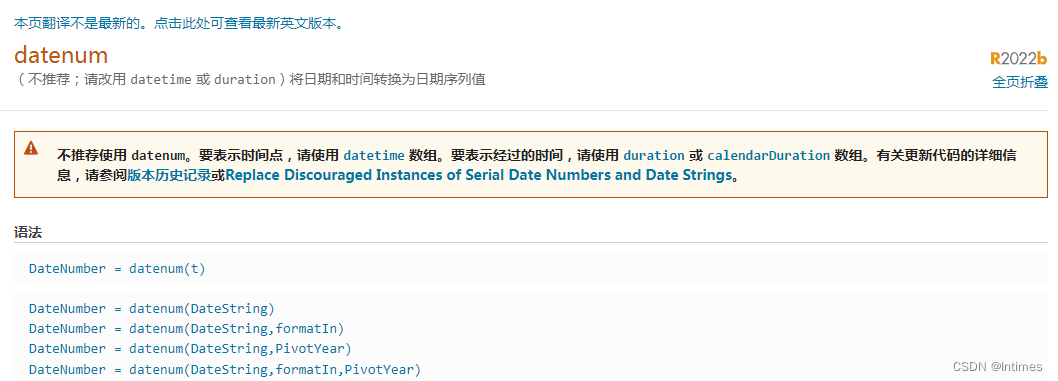
Matlab对日期变量和时间变量的管理
Matlab2012a内置了三个函数 datanumdatevecdatestr 靠这三个函数,可以基本实现日期变量和时间变量的管理。下面直接来看。 (1)datanum 这个函数用来将字符串,日期矢量转为通用日(数值型)。所谓的通用日…...

js字符串 常用方法 并带详细讲解
JavaScript中字符串是一种基本数据类型,表示文本数据。字符串常用方法有以下几种: length:返回字符串的长度。 let str "hello world"; console.log(str.length); // 11indexOf:返回字符串中指定字符或子串的位置&am…...

Oracle_Audit_审计
1、什么是审计审计(Audit)用于监视用户所执行的数据库操作,并且Oracle会将审计跟踪结果存放到OS文件(默认位置为$ORACLE_BASE/admin/$ORACLE_SID/adump/)或数据库(存储在system表空间中的SYS.AUD$表中,可通…...
)
python算法中的深度学习算法之生成对抗网络(详解)
目录 学习目标: 学习内容: 生成对抗网络 Ⅰ. 生成器 Ⅱ. 判别器...
【VM服务管家】VM4.0软件使用_1.2 工具类
目录 1.2.1 文本保存:逐行保存格式化模块输出的方法1.2.2 脚本模块:循环模块搭配脚本使用的方法1.2.3 几何查找:彩色图像的几何查找方法1.2.4 深度学习:图像分割的面积的获取方法1.2.5 颜色识别:使用颜色识别工具做分类…...

Android系统架构
Application层,也就是应用层,不仅包括通话短信联系人这种系统级的应用,还包括用户自己安装的一些第三方应用Framework层,这一层大部分用Java写的,包括系统服务和四大组件Library层,这一层大部分都是C/C写的…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
