软考报名资格审核要多久?证明材料要哪些?
软考报名资格审核要多久?
一般来说,软考资格审核时间不超过1个工作日。当然,每个地区的具体情况都不一样。有些地区估计需要1-3个工作日。总之,为了顺利成功报名,大家应尽快报名,不要拖到最后一天。
软考报名资格审核是网上审批。考试填写信息后,软考相关机构将对考生的报名信息和上传照片进行网上审批。考生需在提交报名信息一个工作日后再次登录报名系统,查看是否已获批(不会有任何电子邮件、短信等形式通知考生是否获批)。如果审批通过,将被视为成功注册。如果审核失败,考生将根据提醒信息进行修改并提交,直至系统提示审批通过。同时,报名时间截止后的修改无效,视为放弃报名。
软考报名审核证明材料要哪些?
河南省:
根据报考属地化管理的原则,申请人必须具有河南省户籍,在河南省相关学校学习,持有河南省居住证或河南省社会保障处于正常支付状态。符合上述条件之一的,可以报考。
云南省:
考试实行属地化管理,仅限于户籍所在地(身份证或户籍簿)或居住地(居住证)在云南省的人员和在云南省学校学习(学信网在线确认)的人员。
四川省:
申请人必须根据填写信息上传中国计算机技术职业资格网络注册系统的相应证件(证明):四川户口簿、四川学生在读证书(加盖院级或学校公章)、四川居住证(加盖公安派出所公章)、四川社会保障证明(加盖社会保障局公章)或四川工作证明(加盖四川公司公章)等属地证明文件原件电子扫描件。
辽宁省:
身份证号码显示非辽宁户籍,但在辽宁省居住、工作或学习的考生必须提供以下三个证明之一:
1.辽宁省公安部门出具的“居住证”;
2.身份证上的地址已改为辽宁省,可直接提供身份证。
在辽宁省大学学习的非辽宁学生应提供学校颁发的“学生身份证”或“学生身份证”(考生姓名、身份证号码、学校学习、经办人姓名、学校固定电话号码、日期等信息)。
3.加盖单位(辽宁省办公地址)公章的“员工在职证书”(考生姓名、身份证号码、在单位工作、经办人姓名、单位固定电话号码、日期等信息);
福建省:
在提交注册信息时,考生必须上传以下三项中的任何一项证明文件:
1.福建省居住证明:本人身份证或居住证在有效期内。
2.福建省社保证明(2022年9月至2023年2月持续6个月)。
3.有效学生证明:考生本人学生证明或学生在校证明。
浙江:
有关证明材料为以下三项中的任何一项:
1.浙江省学校证明:有效期内教育部学籍在线验证报告(登录学信网-学籍查询栏下载)。
2.浙江省居住证:浙江省身份证、户口簿(含户口簿主页及本人页)或浙江省公安部门颁发的“浙江省居住证”;
3.浙江省工作证明:2022年7月至2023年3月持续6个月的浙江省社保证明(登录支付宝“浙里办”-社保服务-打印下载社保证明)。
江苏省:
江苏省考试实行属地化管理。申请人必须在江苏省工作、学习或生活,并在江苏省附近的城市报名参加考试。申请人必须提供三种材料中的任何一种:居住证、工作证或学校证明:
1.江苏省学校证明:有效期内教育部学籍在线验证报告(登录学信网-学籍查询栏下载)。
2.江苏省工作证明:提供2022年10月至2023年3月至少缴纳一个月的江苏社保证明(包含二维码的社保证明可通过江苏智能人社网站/APP或支付宝江苏智能人社小程序中的“个人权益单”功能打印下载)。
3.江苏省居住证:江苏省身份证、户口簿(含户口簿首页及本人页)或江苏省公安部门签发的“江苏省居住证”。
相关文章:

软考报名资格审核要多久?证明材料要哪些?
软考报名资格审核要多久? 一般来说,软考资格审核时间不超过1个工作日。当然,每个地区的具体情况都不一样。有些地区估计需要1-3个工作日。总之,为了顺利成功报名,大家应尽快报名,不要拖到最后一天。 软考…...

2023-04-27 polardbx-LSM-tree的Parallel Recovery性能优化
背景 数据库的Crash Recovery时长关系到数据库的可用性SLA、故障止损时间、升级效率等多个方面。本文描述了针对X-Engine数据库存储引擎的一种Crash Recovery优化手段,在典型场景下可以显著缩短数据库实例的故障恢复时间,提升用户使用感受。 当前面临的问题 X-Engine是阿里…...

创作纪念日让 AI 与我共同记录下今天 — 【第五周年、1460天】
今天正是五一,收到一条消息? 五一还要我加班 😏? 喔,原来是 CSDN 给我发的消息呀!我在 CSDN 不知不觉已经开启第五周年啦! 目录 1.机缘2.收获3.日常4.我与 AI 的“合作”part Ipart II Super al…...

枚举法计算24点游戏
# 请在此处编写代码 # 24点游戏 import itertools# 计算24点游戏代码 def twentyfour(cards):"""(1)itertools.permutations(可迭代对象):通俗地讲,就是返回可迭代对象的所有数学全排列方式。itertools.permutations("1118") -…...

@Cacheable注解
Cacheable注解是Spring框架中提供的一种缓存技术, 用于标记一个方法的返回值可以被缓存起来,当再次调用该方法时,如果缓存中已经存在缓存的结果,则直接从缓存中获取结果而不是再次执行该方法,从而提高系统的性能和响应…...

CentOS分区挂载 fdisk、parted方式解析
1 介绍 在linux中,通常会将持久化数据保存到硬盘当中,但是硬盘一把会比较大,因此我们为了方便管理,会将一个硬盘分成多个逻辑硬盘,称之为分区。 为了能够让分区中的文件使得能让操作系统处理,则需要对分区…...

BuildKit
介绍 BuildKit是一个现代化的构建系统,主要用于构建和打包容器镜像。它是Docker官方的构建引擎,支持构建多阶段构建、缓存管理、并行化构建、多平台构建等功能。BuildKit还支持多种构建语法和格式,包括Dockerfile、BuildKit Build Specifica…...
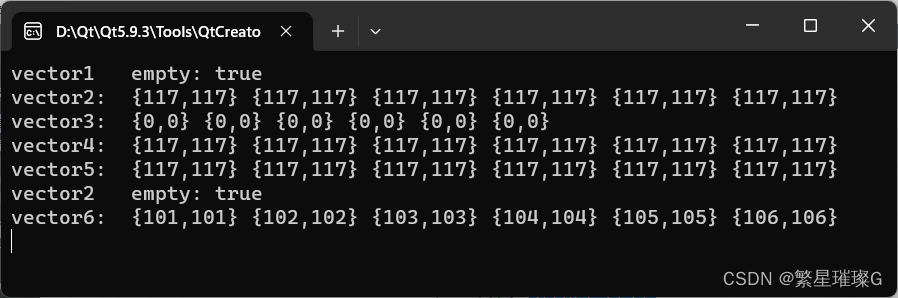
c++ 11标准模板(STL) std::vector (二)
定义于头文件 <vector> template< class T, class Allocator std::allocator<T> > class vector;(1)namespace pmr { template <class T> using vector std::vector<T, std::pmr::polymorphic_allocator<T>>; }(2)(C17…...

Python 循环技巧
目录 在字典中循环时,用 items() 方法可同时取出键和对应的值: 在序列中循环时,用 enumerate() 函数可以同时取出位置索引和对应的值: 同时循环两个或多个序列时,用 zip() 函数可以将其内的元素一一匹配:…...

【Java笔试强训 7】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥Fibona…...
工作7年的程序员,明白了如何正确的“卷“
背景 近两年,出台和落地的反垄断法,明确指出要防止资本无序扩张。 这也就导致现在的各大互联网公司,不能再去染指其他已有的传统行业,只能专注自己目前存量的这些业务。或者通过技术创新,开辟出新的行业。 但创新这…...

数学建模——查数据
如果选择C题的小伙伴常常需要查找一些数据,那么这些数据一般都可以从哪里找到呢? 常用的查数据平台 优先在知网、谷歌学术等平台搜索国家统计局 最全面,月度季度年度,各地区各部门各行业,包罗万象 https://data.stat…...

PAT A1019 General Palindromic Number
1019 General Palindromic Number 分数 20 作者 CHEN, Yue 单位 浙江大学 A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are pa…...
ChatGPT会颠覆SEO内容创作吗
近几年 AI 的发展日新月异。除了搜索算法本身大规模应用人工智能,我也一直关注着 AI 用于写作的进展。 上篇关于 Google 有用内容更新的帖子还在说,高质量内容创作是 SEO 最难的事之一,对某些网站来说,如果能有工具帮助ÿ…...
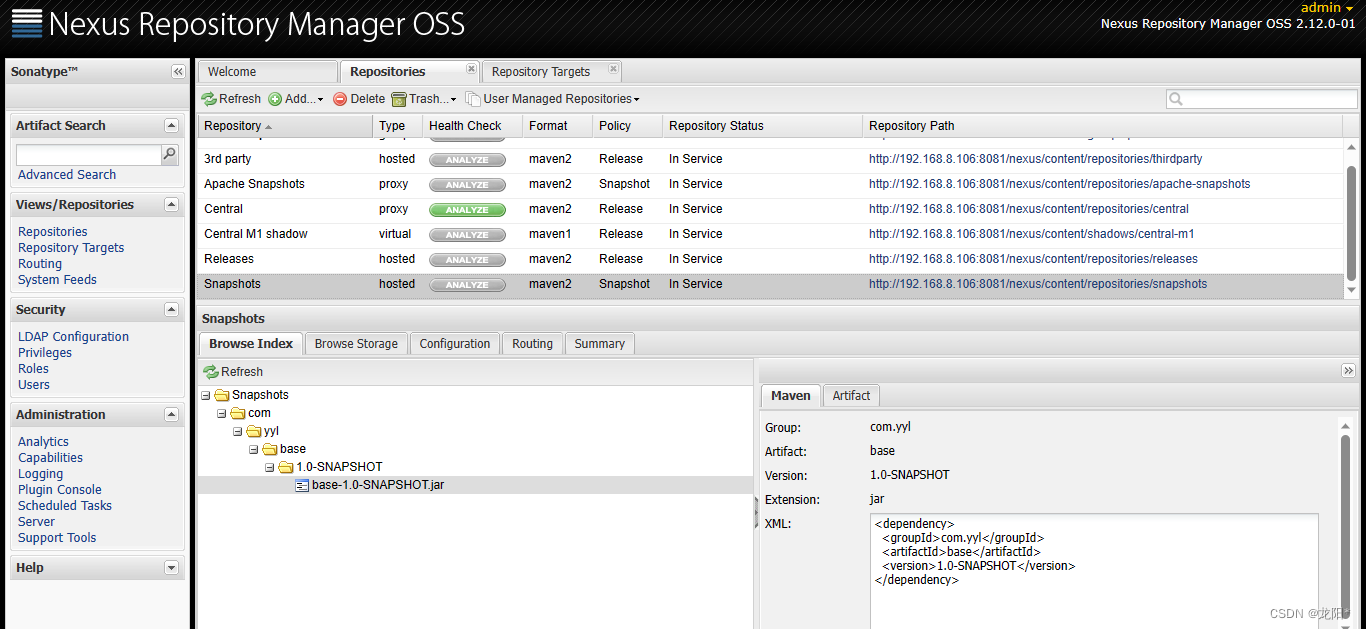
Maven私服搭建
为什么要搭建私服 通常在maven项目的pom.xml文件中引入了某个依赖包之后,maven首先会去本地仓库去搜索,本地仓库搜索不到会去maven的配置文件settings.xml中配置的maven镜像地址去找,比如: <mirrors><!-- mirror| Specif…...
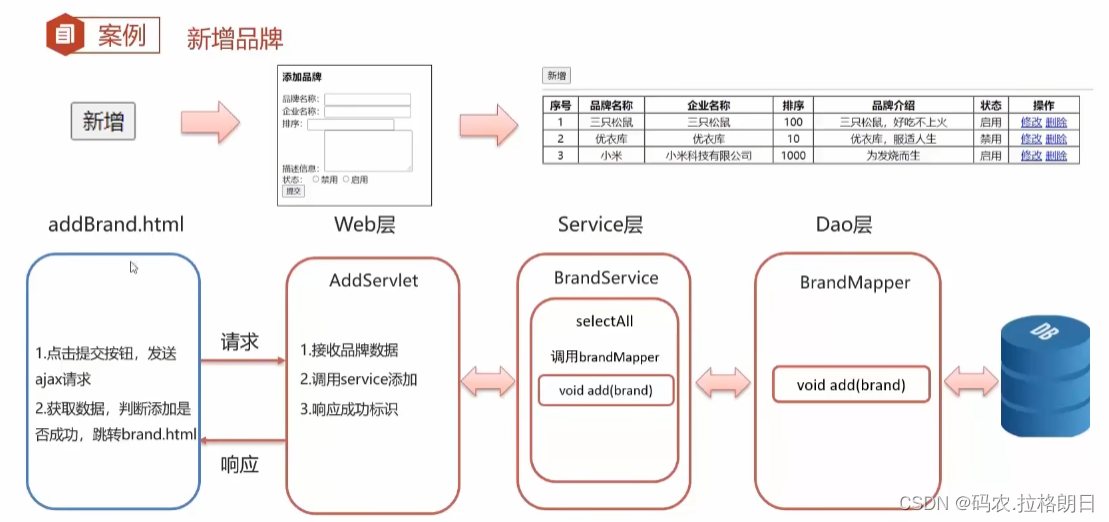
Ajax和Json综合案例
1. 查询所有 创建brand.html,使用axios发送请求,其中查询一般采用get的请求方式 <script src"js/axios-0.18.0.js"></script><script>//1. 当页面加载完成后,发送ajax请求window.onload function () {//2. 发送ajax请求axi…...

【genius_platform软件平台开发】第九十四讲:int64_t的格式化问题(lld和PRId64)
问题起因是在进行上位机软件优化的工作安排时,同事对unsigned long long 类型的时间戳进行了格式化输出优化,从%ull优化为了% PRIu64,我进行代码合并请求处理的时候突然感觉这个可以仔细查一下。查阅到的相关资料如下: * 1. int6…...

多模态之clip
论文:Learning Transferable Visual Models From Natural Language Supervision Github:https://github.com/OpenAI/CLIP OpenAI出品 论文通过网络爬取4亿(image, text)对,使用对比学习的方法训练得到clip(Contrastive Languag…...
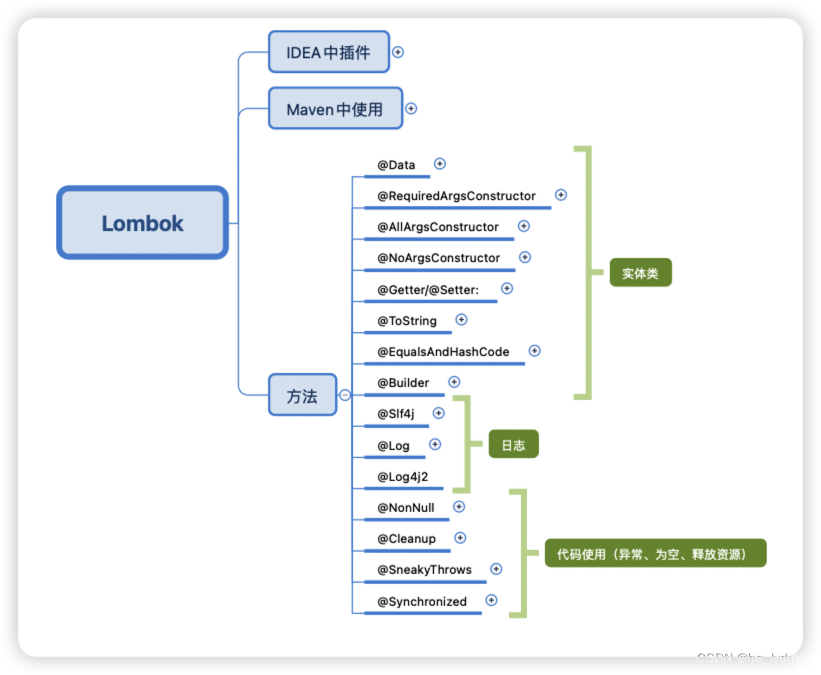
Lombok常用注解
文章目录 一、简介二、Idea中配置三、Maven中配置四、相应注解1、Data2、RequiredArgsConstructor3、AllArgsConstructor4、NoArgsConstructor5、Getter/Setter:6、ToString7、EqualsAndHashCode8、Builder9、NonNull10、Log11、Slf4j12、Log4j213、SneakyThrows14、Cleanup15、…...

加拿大各省接受公立教育的初始年龄汇总 — 供携子女赴加的访学、博后参考
近年来到加拿大从事访问学者和博士后研究的申请者日益增多,有些申请者想带孩子同去上公立学校。因为加拿大各省教育局政策有差异,所以入学(包括学前班)年龄不同,为此知识人网小编整理本文为大家解惑答疑。 加拿大为本国…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
