【机器学习分支】重要性采样(Importance sampling)学习笔记
重要性采样(importance sampling)是一种用于估计概率密度函数期望值的常用蒙特卡罗积分方法。其基本思想是利用一个已知的概率密度函数来生成样本,从而近似计算另一个概率密度函数的期望值。
想从复杂概率分布中采样的一个主要原因是能够使用式(11.1)计算期望。重要采样(importance sampling)的方法提供了直接近似期望的框架,但是它本身并没有提供从概率分布 p ( z ) p(z) p(z)中采样的方法,也就是我们无法从式(11.1)直接过渡到(11.2)
E [ f ] = ∫ f ( z ) p ( z ) d z (11.1) \mathbb{E}[f] = \int f(z)p(z)dz \tag{11.1} E[f]=∫f(z)p(z)dz(11.1) f ^ = 1 L ∑ l = 1 L f ( z ( l ) ) (11.2) \hat{f} = \frac{1}{L}\sum\limits_{l=1}^L f(z^{(l)}) \tag{11.2} f^=L1l=1∑Lf(z(l))(11.2)公式(11.2)给出的期望的有限和近似依赖于能够从概率分布 p ( z ) p(z) p(z)中采样。然而,假设直接从 p ( z ) p(z) p(z)中采样无法完成,但是对于任意给定的 z z z值,我们可以很容易地计算 p ( z ) p(z) p(z)。一种简单的计算期望的方法是将 z z z空间离散化为均匀的格点,将被积函数使用求和的方式计算,形式为
E [ f ] ≃ ∑ l = 1 L p ( z ( l ) ) f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lp(z^{(l)})f(z^{(l)}) E[f]≃l=1∑Lp(z(l))f(z(l))这种方法的一个明显的问题是求和式中的项的数量随着 z z z的维度指数增长。此外,正如我们已经注意到的那样,我们感兴趣的概率分布通常将它们的大部分质量限制在 z z z空间的一个很小的区域,因此均匀地采样非常低效,因为在高维的问题中,只有非常小的一部分样本会对求和式产生巨大的贡献。我们希望从 p ( z ) p(z) p(z)的值较大的区域中采样,或理想情况下,从 p ( z ) f ( z ) p(z)f(z) p(z)f(z)的值较大的区域中采样。
与拒绝采样的情形相同,重要采样基于的是对提议分布 q ( z ) q(z) q(z)的使用,我们很容易从提议分布中采样,如下图所示:

重要采样解决的是计算函数 f ( z ) f(z) f(z)关于分布 p ( z ) p(z) p(z)的期望的问题,其中,从 p ( z ) p(z) p(z)中直接采样比较困难。相反,样本 z ( l ) {z^{(l)}} z(l)从一个简单的概率分布 q ( z ) q(z) q(z)中抽取,求和式中的对应项的权值为 p ( z ( l ) ) / q ( z ( l ) ) p(z^{(l)})/q(z^{(l)}) p(z(l))/q(z(l)),这样就可以还原到从 p ( z ) p(z) p(z)中取样。
上述过程中的式子,我们可以通过 q ( z ) q(z) q(z)中的样本 { z ( l ) } \{z^{(l)}\} {z(l)}的有限和的形式来表示期望
E = ∫ f ( z ) p ( z ) d z = ∫ f ( z ) p ( z ) q ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L p ( z ( l ) ) q ( z ( l ) ) f ( z ( l ) ) \mathbb{E} = \int f(z)p(z)dz \ = \int f(z)\frac{p(z)}{q(z)}q(z)dz \ \simeq \frac{1}{L}\sum\limits_{l=1}^L\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)}) E=∫f(z)p(z)dz =∫f(z)q(z)p(z)q(z)dz ≃L1l=1∑Lq(z(l))p(z(l))f(z(l))其中 r l = p ( z ( l ) ) / q ( z ( l ) ) r_l = p(z^{(l)}) / q(z^{(l)}) rl=p(z(l))/q(z(l))被称为重要性权重(importance weights),修正了由于从错误的概率分布 q ( z ) q(z) q(z)中采样引入的偏差。
对于上述过程,举个栗子:
我们的待计算函数为 h ( x ) = e − 2 ∣ x − 5 ∣ h(x)=e^{-2|x-5|} h(x)=e−2∣x−5∣,待采样分布为 p ( x ) = 1 10 , x ∼ u ( 0 , 10 ) p(x)=\dfrac{1}{10} ,x \sim\mathcal{u}(0,10) p(x)=101,x∼u(0,10),从 h ( x ) h(x) h(x)的图像中明显可以看出,在中间部分的 h ( x ) p ( x ) h(x)p(x) h(x)p(x)对期望贡献较大,而两边几乎可以忽略不计,所以此时使用均匀分布采样并不合理。

基于此,我们引入了新的采样分布函数 q ( x ) = 1 2 π e − ( x − 5 ) 2 2 q(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{(x-5)^2}{2}} q(x)=2π1e−2(x−5)2

这使得在 h ( x ) h(x) h(x)较大的位置取值更多,需要的采样点更少。
而更常见的情形是,概率分布 p p p的计算结果没有标准化,也就是 p ( z ) = p ~ ( z ) / Z p p(z) = \tilde{p}(z) / Z_p p(z)=p~(z)/Zp中我们只知道 p ~ ( z ) \tilde{p}(z) p~(z),其中 p ~ ( z ) \tilde{p}(z) p~(z)可以很容易地由 z z z计算出来(可能没有函数表达式),而 Z p Z_p Zp未知( p ~ ( z ) \tilde{p}(z) p~(z)无法积分算)。类似的,我们可能希望使用重要采样分布 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq中的 q ~ ( z ) \tilde{q}(z) q~(z),它具有相同的性质。于是我们得到:
E [ f ] = ∫ f ( z ) p ( z ) d z = Z q Z p ∫ f ( z ) p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ Z q Z p 1 L ∑ l = 1 L r ~ l f ( z ( l ) ) \mathbb{E}[f] = \int f(z)p(z)dz \ = \frac{Z_q}{Z_p}\int f(z)\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{Z_q}{Z_p}\frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_lf(z^{(l)}) E[f]=∫f(z)p(z)dz =ZpZq∫f(z)q~(z)p~(z)q(z)dz ≃ZpZqL1l=1∑Lr~lf(z(l))
其中 r ~ l = p ~ ( z ( l ) ) / q ~ ( z ( l ) ) \tilde{r}_l = \tilde{p}(z^{(l)}) / \tilde{q}(z^{(l)}) r~l=p~(z(l))/q~(z(l))。
我们还可以使用同样的样本集合来计算比值 Z p / Z q Z_p / Z_q Zp/Zq,结果为:
Z p Z q = 1 Z q ∫ p ~ ( z ) d z = ∫ p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L r ~ l \frac{Z_p}{Z_q} = \frac{1}{Z_q}\int\tilde{p}(z)dz = \int\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_l ZqZp=Zq1∫p~(z)dz=∫q~(z)p~(z)q(z)dz ≃L1l=1∑Lr~l
第一个等式中 Z p Z_p Zp用 ∫ p ~ ( z ) d z \int\tilde{p}(z)dz ∫p~(z)dz等价计算了出来,第二个等式中 Z q Z_q Zq用 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq替代
因此:
E [ f ] ≃ ∑ l = 1 L w l f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lw_lf(z^{(l)}) E[f]≃l=1∑Lwlf(z(l))其中: w l = r ~ l ∑ m r ~ m = p ~ ( z ( l ) ) / q ( z ( l ) ) ∑ m p ~ ( z ( l ) ) / q ( z ( l ) ) w_l = \frac{\tilde{r}_l}{\sum_m\tilde{r}_m} = \frac{\tilde{p}(z^{(l)})/q(z^{(l)})}{\sum_m\tilde{p}(z^{(l)})/q(z^{(l)})} wl=∑mr~mr~l=∑mp~(z(l))/q(z(l))p~(z(l))/q(z(l))
这也就是我们最终要找样本点计算的式子
最终,我们达到了“利用一个已知的概率密度函数 q ( z ) q(z) q(z)来生成样本,从而近似计算另一个概率密度函数的期望值 E [ f ] = ∫ f ( z ) p ( z ) d z \mathbb{E}[f] = \int f(z)p(z)dz E[f]=∫f(z)p(z)dz”这一目的。
参考:
- 【PRML】【模式识别和机器学习】【从零开始的公式推导】11.1.4重要性采样 11.1.5采样-重要性-重采样 11.1.6采样与EM算法
- Importance Sampling - VISUALLY EXPLAINED with EXAMPLES!
相关文章:

【机器学习分支】重要性采样(Importance sampling)学习笔记
重要性采样(importance sampling)是一种用于估计概率密度函数期望值的常用蒙特卡罗积分方法。其基本思想是利用一个已知的概率密度函数来生成样本,从而近似计算另一个概率密度函数的期望值。 想从复杂概率分布中采样的一个主要原因是能够使用…...

三角回文数+123
三角回文数:用户登录 问题描述 对于正整数 n, 如果存在正整数 k 使得 n123⋯kk(k1)/2, 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066123⋯363 。 如果一个整数从左到右读出所有数位上的数字, 与从右到左读出所有数位 上的数字是一样的, 则称这个数为…...

JAVA常用的异步处理方法总结
前言 在java项目开发过程中经常会遇到比较耗时的任务,通常是将这些任务做成异步操作,在java中实现异步操作有很多方法,本文主要总结一些常用的处理方法。为了简化,我们就拿一个实际的案例,再用每种方法去实现…...

GitLab统计代码量
gitlab官方文档:https://docs.gitlab.com/ee/api/index.html 1、生成密钥 登录gitlab,编辑个人资料,设置访问令牌 2、获取当前用户所有可见的项目 接口地址 GET请求 http://gitlab访问地址/api/v4/projects?private_tokenxxx 返回参数 …...

Linux TCP MIB统计汇总
概述 在 linux > 4.7 才将所有TCP丢包收敛到 函数 tcp_drop 中 指标详解 cat /proc/net/netstat 格式化命令 cat /proc/net/netstat | awk (f0) {name$1; i2; while ( i<NF) {n[i] $i; i }; f1; next} (f1){ i2; while ( i<NF){ printf "%s%s %d\n", …...

记录 docker linux部署jar
第一步 web sso user admin 中yml文件还原到阿里mysql数据库 第二步 各个jar进行打包处理 第三步 正式服务器的Jar备份 第四步 拉取以上jar包 到正式服务器中 第五步 查看 docker images 其中 web_service 1.0.2是上一个版本 上一个版本build 镜像命令是这样的(需…...

【Linux】教你用进程替换制作一个简单的Shell解释器
本章的代码可以访问这里获取。 由于程序代码是一体的,本章在分开讲解各部分的实现时,代码可能有些跳跃,建议在讲解各部分实现后看一下源代码方便理解程序。 制作一个简单的Shell解释器 一、观察Shell的运行状态二、简单的Shell解释器制作原理…...

onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行
onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行 可以尝试在 onMeasure 方法中重写 measureChildWithMargins 或 measureChild 方法来实现这个需求。 对于只有一个字的 View,我们可以把它的宽度设为屏幕宽度,高度设为最大高度,这样这个 View 就会占满一整行…...
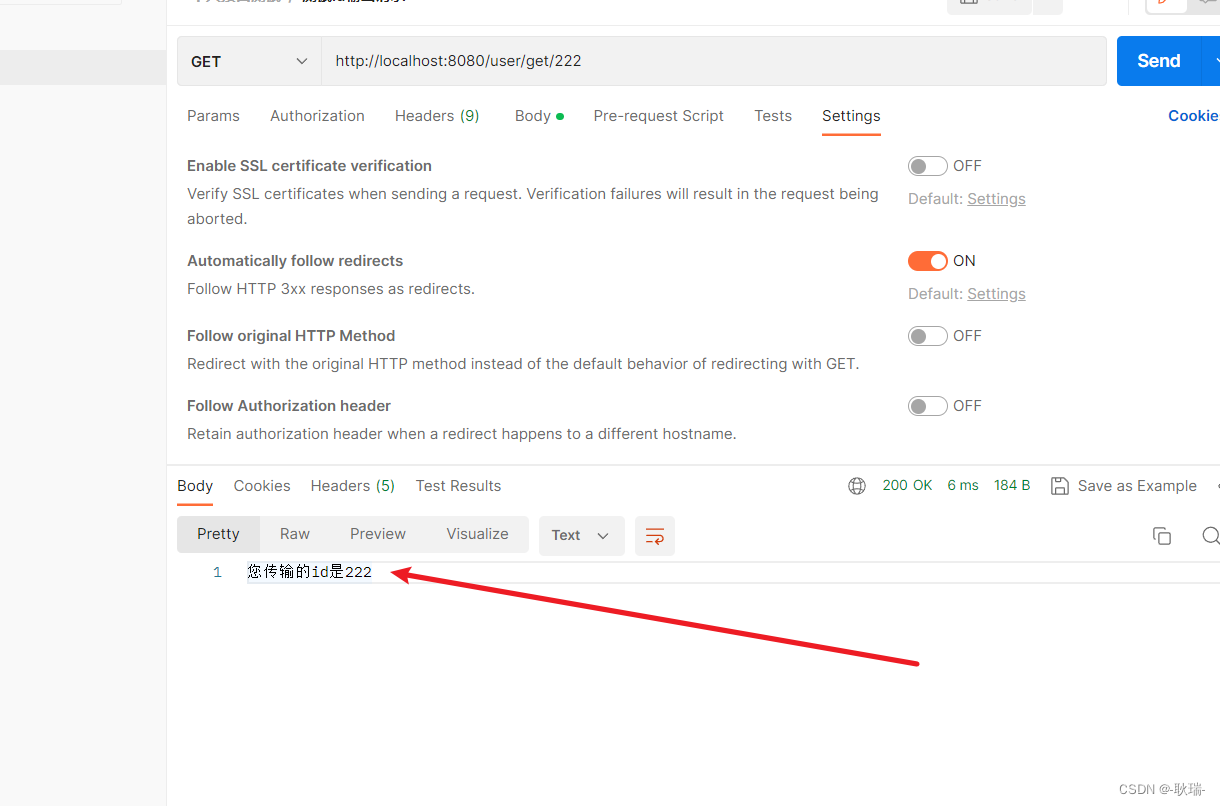
Postman创建项目 对接口发起请求处理
查看本文之前 您需要理解了解 Postman 的几个简单工作区 如果还没有掌握 可以先查看我的文章 简单认识 Postman界面操作 那么 掌握之后 我们就可以正式来开启我们的接口测试 我们先选择 Collections 我们点上面这个加号 多拉一个项目出来 然后 我们选我们刚加号点出来的项目…...

在Vue3项目中js-cookie库的使用
文章目录 前言1.安装js-cookie库2.引入、使用js-cookie库 前言 今天分享一下在Vue3项目中引入使用js-cookie。 1.安装js-cookie库 js-cookie官网 安装js-cookie,输入 npm i js-cookie安装完成可以在package.json中看到: 安装以后,就可…...

【论文笔记】Attention和Visual Transformer
Attention和Visual Transformer Attention和Transformer为什么需要AttentionAttention机制Multi-head AttentionSelf Multi-head Attention,SMA TransformerVisual Transformer,ViT Attention和Transformer Attention机制在相当早的时间就已经被提出了&…...

独立IP服务器和共享IP服务器有什么区别
在选择一个合适的服务器时,最常见的选择是共享IP服务器和独立IP服务器。尽管两者看起来很相似,但它们有着很大的不同。本文将详细介绍共享IP服务器和独立IP服务器的不同之处,以及如何选择适合您需求的服务器。 一、什么是共享IP服务器? 共享…...

Java8
Java8 (一)、双列集合(二)、Map集合常用api(三)、Map集合的遍历方式(四)、HashMap(五)、LinkedHashMap(六)、TreeMap(七&a…...

nn.conv1d的输入问题
Conv1d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue) in_channels(int) – 输入信号的通道。在文本分类中,即为词向量的维度out_channels(int) – 卷积产生的通道。有多少个out_channels,就需要多少个1维…...
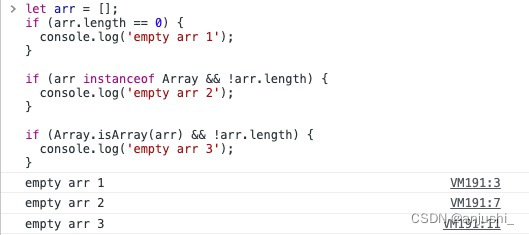
js判断是否为null,undefined,NaN,空串或者空对象
js判断是否为null,undefined,NaN,空串或者空对象 这里写目录标题 js判断是否为null,undefined,NaN,空串或者空对象特殊值nullundefinedNaN空字符串("")空对象(…...

Java每日一练(20230501)
目录 1. 路径交叉 🌟🌟 2. 环形链表 🌟🌟 3. 被围绕的区域 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏…...

从零开始学习Web自动化测试:如何使用Selenium和Python提高效率?
B站首推!2023最详细自动化测试合集,小白皆可掌握,让测试变得简单、快捷、可靠https://www.bilibili.com/video/BV1ua4y1V7Db 目录 引言: 一、了解Web自动化测试的基本概念 二、选择Web自动化测试工具 三、学习Web自动化测试的…...

fastdfs环境搭建
安装包下载路径 libfastcommon下载地址:https://github.com/happyfish100/libfastcommon/releasesFastDFS下载地址:https://github.com/happyfish100/fastdfs/releasesfastdfs-nginx-module下载地址:https://github.com/happyfish100/fastdf…...

有什么牌子台灯性价比高?性价比最高的护眼台灯
由心感叹现在的孩子真不容易,学习压力比我们小时候大太多,特别是数学,不再是简单的计算,而更多的是培养学生其他思维方式,有时候我都觉得一年级数学题是不是超纲了。我女儿现在基本上都是晚上9点30左右上床睡觉&#x…...

信息系统项目管理师 第9章 项目范围管理
1.管理基础 1.产品范围和项目范围 产品范围:某项产品、服务或成果所具有的特征和功能。根据产品需求来衡量。 项目范围:包括产品范围,是为交付具有规定特性与功能的产品、服务或成果而必须完成的工作。项目管理计划来衡量 2.管理新实践 更加注重与商业分析师一起…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
