机器人学一些知识
机器人动力学模型是用数学方法描述机器人运动和力学特性的模型。它包含机器人的几何结构、质量、惯性、摩擦等物理特性,以及机器人的控制系统和传感器等。机器人动力学模型可以用于机器人的运动规划、控制算法设计、仿真和优化等应用中。
机器人动力学模型通常采用牛顿-欧拉法或拉格朗日方程等力学模型进行建模。牛顿-欧拉法是一种递归算法,可以逐个关节地计算机器人的动力学参数,包括关节角度、速度、加速度、力和扭矩等。拉格朗日方程则是一种基于能量守恒原理的方法,可以将机器人的动力学问题转化为求解Lagrange函数的极值问题,从而得到机器人的运动方程和约束条件。
机器人动力学模型的建立需要考虑多种因素,如机器人的结构、质量分布、运动范围、关节限制、摩擦力等。同时,还需要考虑机器人的控制系统和传感器的影响,如控制器的延迟、传感器的噪声等。因此,机器人动力学模型的建立是一个复杂的过程,需要进行详细的分析和验证。
以下是一个简单的例子,用牛顿-拉格朗日法建立一个二自由度机械臂的动力学模型。
-
确定机器人的几何结构和运动自由度。假设机械臂有两个旋转关节,分别为关节1和关节2,且关节2位于关节1的末端,机械臂在三维空间中能够绕x轴和y轴旋转,因此机械臂的运动自由度为2。
-
确定机器人的质量、惯性和摩擦系数。假设机械臂的质量和惯性参数如下:
- 关节1的质量为m1,质心距离关节1轴线的距离为l1,惯性矩阵为I1。
- 关节2的质量为m2,质心距离关节2轴线的距离为l2,惯性矩阵为I2。
假设机械臂的摩擦系数为0。
- 根据牛顿定律建立机器人的动力学方程。根据牛顿定律,机械臂的动力学方程可以表示为:
- 关节1:m1l1^2θ1’’ + (m1l2^2 + m2l2^2 + 2m2l1l2cosθ2)θ1’’ + (m2l2^2 + m2l1l2cosθ2)θ2’’ = τ1
- 关节2:m2l2^2θ2’’ + m2l1l2cosθ2θ1’’ + m2l1l2sinθ2(θ1’ + θ2’)^2 = τ2
其中,θ1和θ2分别表示关节1和关节2的角度,θ1’和θ2’分别表示关节1和关节2的角速度,θ1’‘和θ2’'分别表示关节1和关节2的角加速度,τ1和τ2分别表示关节1和关节2的扭矩。
- 根据拉格朗日方程建立机器人的动力学模型。根据拉格朗日方程,机械臂的动力学模型可以表示为:
L = T - V
其中,T表示机械臂的动能,V表示机械臂的势能。机械臂的动能和势能可以表示为:
- 动能:T = 1/2(m1l1^2 + I1)θ1’^2 + 1/2(m2l1^2 + m2l2^2 + I2 + 2m2l1l2cosθ2)θ1’^2 + 1/2(m2l2^2 + I2)θ2’^2 + m2l1l2cosθ2θ1’θ2’
- 势能:V = -m1gl1cosθ1 - m2g(l1cosθ1 + l2cos(θ1 + θ2))
其中,g表示重力加速度。
然后,通过拉格朗日方程求解机械臂的运动方程和约束条件。
-
进行模型验证和优化。通过模拟仿真和实验验证机械臂动力学模型的准确性和可靠性,并对模型进行优化和改进。
以下是一个简单的例子,用牛顿-拉格朗日法建立一个二自由度机械臂的动力学模型。 -
确定机器人的几何结构和运动自由度。假设机械臂有两个旋转关节,分别为关节1和关节2,且关节2位于关节1的末端,机械臂在三维空间中能够绕x轴和y轴旋转,因此机械臂的运动自由度为2。
-
确定机器人的质量、惯性和摩擦系数。假设机械臂的质量和惯性参数如下:
- 关节1的质量为m1,质心距离关节1轴线的距离为l1,惯性矩阵为I1。
- 关节2的质量为m2,质心距离关节2轴线的距离为l2,惯性矩阵为I2。
假设机械臂的摩擦系数为0。
- 根据牛顿定律建立机器人的动力学方程。根据牛顿定律,机械臂的动力学方程可以表示为:
- 关节1:m1l1^2θ1’’ + (m1l2^2 + m2l2^2 + 2m2l1l2cosθ2)θ1’’ + (m2l2^2 + m2l1l2cosθ2)θ2’’ = τ1
- 关节2:m2l2^2θ2’’ + m2l1l2cosθ2θ1’’ + m2l1l2sinθ2(θ1’ + θ2’)^2 = τ2
其中,θ1和θ2分别表示关节1和关节2的角度,θ1’和θ2’分别表示关节1和关节2的角速度,θ1’‘和θ2’'分别表示关节1和关节2的角加速度,τ1和τ2分别表示关节1和关节2的扭矩。
- 根据拉格朗日方程建立机器人的动力学模型。根据拉格朗日方程,机械臂的动力学模型可以表示为:
L = T - V
其中,T表示机械臂的动能,V表示机械臂的势能。机械臂的动能和势能可以表示为:
- 动能:T = 1/2(m1l1^2 + I1)θ1’^2 + 1/2(m2l1^2 + m2l2^2 + I2 + 2m2l1l2cosθ2)θ1’^2 + 1/2(m2l2^2 + I2)θ2’^2 + m2l1l2cosθ2θ1’θ2’
- 势能:V = -m1gl1cosθ1 - m2g(l1cosθ1 + l2cos(θ1 + θ2))
其中,g表示重力加速度。
然后,通过拉格朗日方程求解机械臂的运动方程和约束条件。
- 进行模型验证和优化。通过模拟仿真和实验验证机械臂动力学模型的准确性和可靠性,并对模型进行优化和改进。
假设有一个双关节机械臂,其质量分别为 m 1 m_1 m1和 m 2 m_2 m2,长度分别为 l 1 l_1 l1和 l 2 l_2 l2,关节角度分别为 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2,关节角速度分别为 θ 1 ˙ \dot{\theta_1} θ1˙和 θ 2 ˙ \dot{\theta_2} θ2˙,关节角加速度分别为 θ 1 ¨ \ddot{\theta_1} θ1¨和 θ 2 ¨ \ddot{\theta_2} θ2¨,重力加速度为 g g g。
根据牛顿欧拉方法,机器人动力学模型可以表示为:
m 1 l 1 2 θ 1 ¨ + m 2 ( l 1 2 θ 1 ¨ + l 2 2 θ 2 ¨ + 2 l 1 l 2 cos ( θ 1 − θ 2 ) θ 1 ˙ θ 2 ˙ ) + ( m 1 + m 2 ) g l 1 sin ( θ 1 ) = τ 1 m 2 l 2 2 θ 2 ¨ + m 2 l 1 l 2 cos ( θ 1 − θ 2 ) θ 1 ¨ + m 2 g l 2 sin ( θ 2 ) = τ 2 \begin{aligned} m_1 l_1^2 \ddot{\theta_1} + m_2 (l_1^2 \ddot{\theta_1} + l_2^2 \ddot{\theta_2} + 2l_1 l_2 \cos(\theta_1 - \theta_2) \dot{\theta_1} \dot{\theta_2}) + (m_1 + m_2) g l_1 \sin(\theta_1) &= \tau_1 \\ m_2 l_2^2 \ddot{\theta_2} + m_2 l_1 l_2 \cos(\theta_1 - \theta_2) \ddot{\theta_1} + m_2 g l_2 \sin(\theta_2) &= \tau_2 \end{aligned} m1l12θ1¨+m2(l12θ1¨+l22θ2¨+2l1l2cos(θ1−θ2)θ1˙θ2˙)+(m1+m2)gl1sin(θ1)m2l22θ2¨+m2l1l2cos(θ1−θ2)θ1¨+m2gl2sin(θ2)=τ1=τ2
其中, τ 1 \tau_1 τ1和 τ 2 \tau_2 τ2分别为关节1和关节2的扭矩。
可以使用这个模型来计算机器人在不同关节角度下的运动状态和所需扭矩,从而进行运动规划和控制。
相关文章:

机器人学一些知识
机器人动力学模型是用数学方法描述机器人运动和力学特性的模型。它包含机器人的几何结构、质量、惯性、摩擦等物理特性,以及机器人的控制系统和传感器等。机器人动力学模型可以用于机器人的运动规划、控制算法设计、仿真和优化等应用中。 机器人动力学模型通常采用…...
应用,auto,内联函数
6.引用: //指针 int main() {int a 0;int& b a;int& c b;int& d c;cout << &a << endl;cout << &b << endl;cout << &c << endl;cout << &d << endl;b;d;cout << a <<…...

Flask框架的学习---01
1.工程搭建: (1) 安装flask: pip3 install flask (2)命令行: (1)终端运行:flask run (2)绑定IP地址和端口:Flask run -h 127.0.0.1 -p 8083 修改端口号 (3࿰…...
免费gpt-4-国内使用gpt-4
如何用上gpt-4 GPT-4尚未正式发布和公开,因此我们无法提供对GPT-4的具体使用方法。但是,可以从GPT-4的前一代——GPT-3的使用经验和GPT-4的预期功能来看,建议如下: 了解GPT-4的语言处理能力和适用场景:GPT-4预计将进一…...
《程序员面试金典(第6版)面试题 16.09. 运算
题目描述 请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。 你的实现应该支持如下操作: Operations() 构造函数minus…...

asp.net基于web的校园美食派送配送系统
1.系统登录:系统登录是用户访问系统的路口,设计了系统登录界面,包括用户名、密码和验证码,然后对登录进来的用户判断身份信息,判断是管理员用户还是普通用户。 2.系统用户管理:不管是…...

【JAVA】#详细介绍!!! 文件操作之File对象(1)!
本文内容不涉及文件内容操作,主要是对指定文件元信息的获取,以及通过java代码如何创建一个文件或者删除文件 目录 文件操作的File对象 File对象的基本操作方法 得到文件(夹)对象的信息元 1.getParent 2. getName 3.getPath 4…...

Vue基本的内置指令
前言 除了常见的v-bind,v-for,v-if,v-on.v-model等,本次学习一些vue提供的其他内置指令 1 v-text 给标签插入文本,类似于插值语法 它会把全部的字符串当成文本去解析,不会当成标签的,哪怕写的是标签结构 效果和插值语法是一样的 插值语法比v-text更加…...

华为孟晚舟当值首秀:2030年AI算力将增长500倍!
作者 | 范智林 来源 | 华商观察 微信号:HuashangGC 孟晚舟当值首次亮相。 4月19日,华为副董事长、轮值董事长、CFO孟晚舟在华为第20届全球分析师大会上进行演讲,这是她当值华为轮值董事长以来的首次公开亮相。 按照华为内部规定,…...

关于python异常的总结
Python异常是在程序执行时发生的错误,可能会导致程序终止运行。 在Python中,异常处理是一种机制,它允许开发人员在程序发生异常时捕获、处理和报告这些异常,以便程序可以继续运行或在出现异常时进行优雅的退出。 在Python中&…...
基于Java+SpringBoot+vue学生学习平台详细设计实现
基于JavaSpringBootvue学生学习平台详细设计实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式 文章目…...

【云原生网关】Kong 使用详解
目录 一、前言 二、Kong介绍 三、Kong核心组件 3.1 kong组件介绍 3.1.1 Kong Server 3.1.2 Apache Cassandra/PostgreSQL 3.1.3 Kong dashboard 3.2 传统网关与Kong工作模式对比 四、Kong网关特征与架构 4.1 kong网关特征 4.1.1 可扩展性 4.1.2 模块化 4.1.3 在任…...

浅谈之Java多线程
Java多线程是Java语言中一个非常重要的特性,它允许程序同时执行多个任务。通过多线程,程序可以同时处理多项任务,从而缩短程序的执行时间。另外,多线程也有助于利用多核处理器,更好地发挥计算机硬件的性能。 那我们在…...

【Vue3学习笔记1】一个清单应用帮你入门Vue.js
Vue 目前已经是国内最流⾏的前端框架之⼀,Vue 3 带来的诸多优化更是让前端圈迎来了新的潮流,比如: 基于 Proxy 的全新响应式实现; Composition API <script setup> 组织代码的更优方式; 更有料的 TypeScript 支…...

go破冰之旅·8·go函数基本实践及各种玩法
一次5-10分钟即可搞定,以干货效率的学习方式带你更直观的玩转各种玩法! 行文不易,一字一句纯手打创造,倾注了不少精力,感谢支持。 目录 什么是函数?有哪些元素? 函数参数、返回值 小程序&…...
Qt - 从零到壹的 打地鼠 游戏
❤️🔥欢迎收看西北风的blog,好男人就是我,我就是西北风。✨ Gitee 地址 W_A_Mole NTC_jason/cc语言 - 码云 - 开源中国 (gitee.com) 目录 🟥一:创建一个主窗体 🟣二.:添加主窗口背景图片…...
代码自动发布系统
之前是jenkins发现gitlab代码更新了就自动获取直接部署到服务器 现在是jenkins自动获取Code之后打包成镜像上传到仓库然后通知docker去拉取更新的镜像 分析 旧∶ 代码发布环境提前准备,以主机为颗粒度静态 新: 代码发布环境多套,以容器为颗粒度编译 …...
——安装)
qemu-基础篇(一)——安装
文章目录 env安装查看版本查看支持的开发板查看支持的CPU的型号 env ubuntu 安装 sudo apt-get install qemu sudo apt-get install qemu-system-arm sudo apt-get install qemu-system查看版本 qemu-img -V qemu-system-arm --version qemu-system-aarch64 --version返回结…...
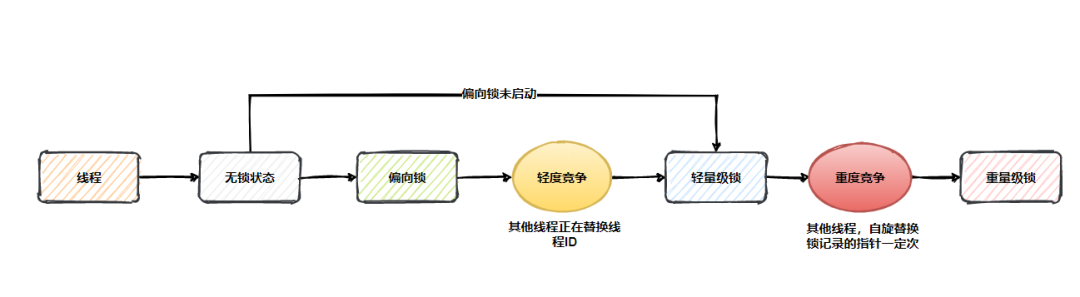
从根本上理解Synchronized的加锁过程
作为一个Java开发,对于Synchronized这个关键字并不会陌生,无论是并发编程,还是与面试官对线,Synchronized可以说是必不可少。 在JDK1.6之前,都认为Synchronized是一个非常笨重的锁,就是在之前的《谈谈Java…...
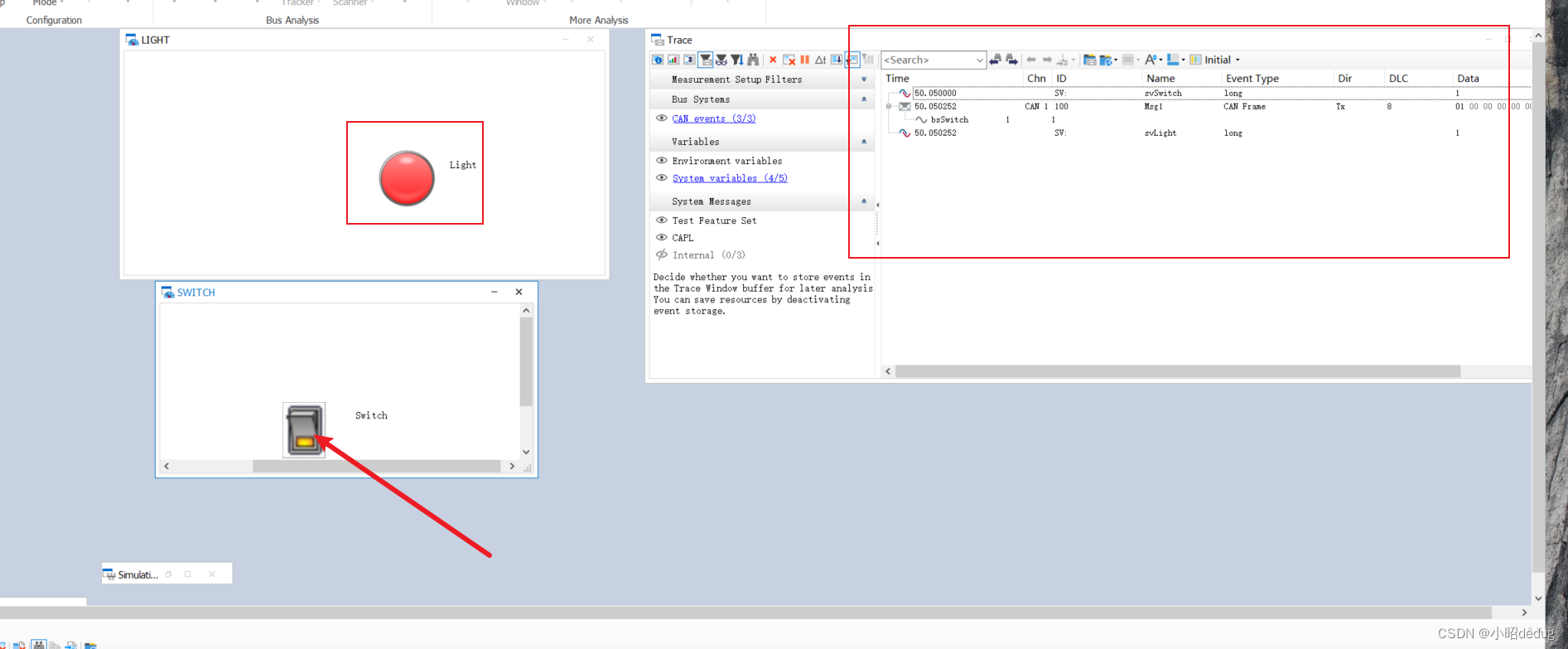
CANOE入门到精通——CANOE系列教程记录1 第一个仿真工程
本系列以初学者角度记录学习CANOE,以《CANoe开发从入门到精通》参考学习,CANoe16 demo版就可以进行学习 概念 CANoe是一种用于开发、测试和分析汽车电子系统的软件工具。它通过在不同层次上模拟汽车电子系统中的不同部件,如ECU、总线和传感…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...
