浙大数据结构与算法一些有意思的理论基础题
堆栈
有人给出了堆栈用数组实现的另一种方式,即直接在函数参数中传递数组和top变量(而不是两者组成的结构指针),其中Push操作函数设计如下。这个Push函数正确吗?为什么?
#define MaxSize 100
ElementType S[MaxSize];
int top;
void Push(ElementType *S, int top, ElementType item)
{ if (top==MaxSize-1) {
printf(“堆栈满”); return;
}else {
S[++top] = item;
return;
}
}
分析:
问题出在函数参数的设计上。在函数定义中,数组S和变量top被作为参数传递。这意味着函数使用的是参数中的本地副本而不是全局变量。因此,Push函数实际上并没有改变全局变量top的值,也没有将新元素添加到堆栈中。
队列:
现采用大小为10的数组实现一个循环队列。设在某一时刻,队列为空且此时front和rear值均为5。经过若干操作后,front为8,rear为2,问:此时队列中有多少个元素?答案是4
分析:
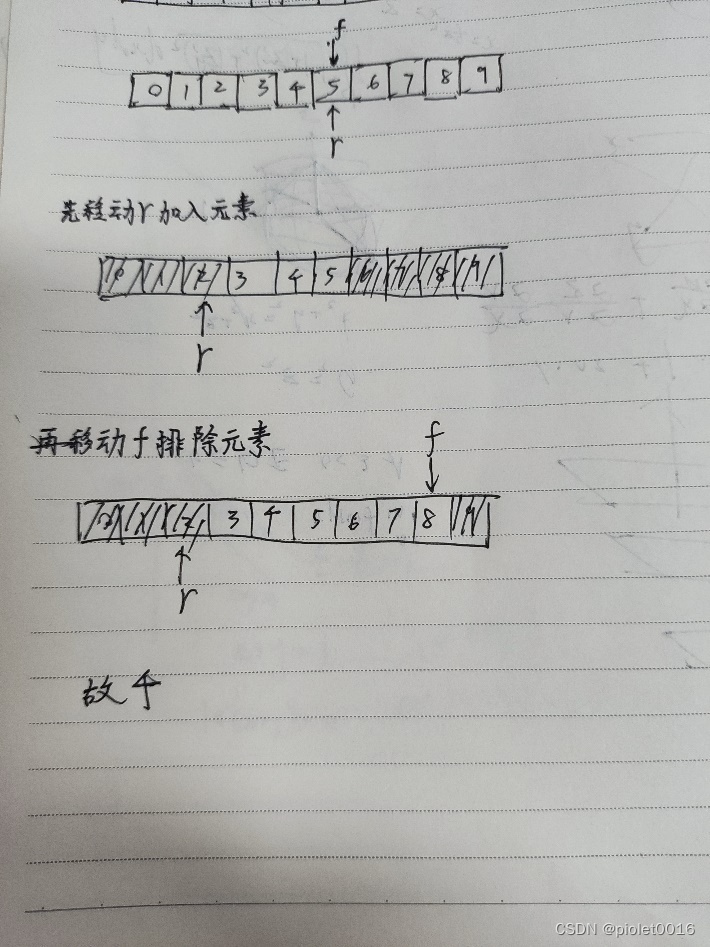
二叉树:
在用“儿子-兄弟”法表示的树中,如果从根结点开始访问其“次子”的“次子”,所经过的结点数与下面哪种情况一样?(注意:比较的是结点数,而不是路径)
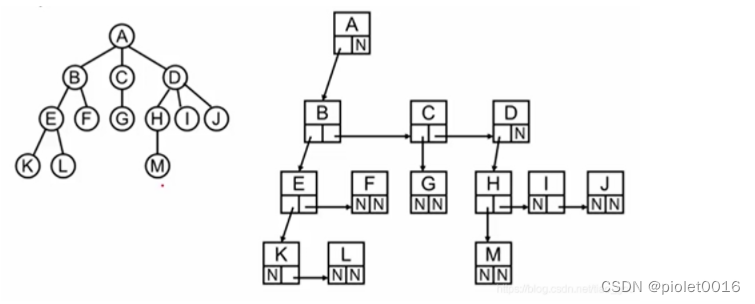
A.从根结点开始访问其“长子”的“长子”
B.从根结点开始访问其“长子”的“长子”的“长子”
C.从根结点开始访问其“长子”的“长子”的“长子”的“长子”
D.不能确定,要看具体树结构
注意不一定是二叉树,默认从左边第一个是长子,余下是次子
正确答案:C
有一个m棵树的集合(也叫森林)共有k条边,问这m颗树共有多少个结点?
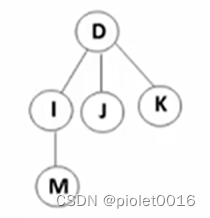
如图,该树一共有5个节点,并且有4条边,对应对于根节点的四个子节点。因为根节点是没有边的。
每个树都有一个根节点,所以m颗树,一共有m个根节点,再加上一共有k条边,有k个子节点,总共m+k个节点。
在分量1~11的数组中按从小到大顺序存放11个元素,如果用顺序查找和二分查找分别查找这11个元素,哪个位置的元素在这两种方法的查找中总次数最少?
A.1
B.2
C.3
D.6
答案:A:
注意是求和
在分量1~11的数组中按从小到大顺序存放11个元素,如果进行二分查找,查找次数最少的元素位于什么位置?
A.1
B.5
C.6
D.11
答案:C
注意不是从0开始排
一棵度(节点的度:依次节点为根节点的子树个数;树的度:树的所有节点中最大的度数)为 m的树有n个节点。若每个节点直接用m个链指向相应的儿子,则表示这个树所需要的总空间是n*(m+1) (假定每个链以及表示节点的数据域都是一个单位空间).。当采用儿子/兄弟(First Child/Next Sibling)表示法时,所需的总空间是:
A.3n
B.2n
C.n*m
D.n*(m-1)
答案:A
首先理解题干表示这个树所需要的总空间是n*(m+1),拆开更好理解:
n * m条链 + n个节点
现在考虑儿子/兄弟表示法,把n个节点串联起来,因为每个节点都有两个部分组成,一个是指向下一个兄弟节点,一个是指向子节点,所以在树中,每个节点有两条链,加上n个节点本身,一共需要3n个空间。
有一颗二叉树,其有两个儿子的结点个数为15个,只有一个儿子的结点个数为32个,问该二叉树的叶子结点个数是多少?
A.15
B.16
C.17
D.32
首先存在关系 n0 = n2 + 1 ,即叶结点个数等于有2个儿子的结点个数+1
所以15 + 1 = 16
如果一个完全二叉树最底下一层为第六层(根为第一层)且该层共有8个叶结点,那么该完全二叉树共有多少个结点?
A.31
B.39
C.63
D.71
对于一颗完全二叉树,其叶节点的数量等于最后一层节点数量的总和。因此,该完全二叉树共有8个叶节点,则最后一层共有8个节点。而对于完全二叉树,从根节点到倒数第二层为满二叉树,且节点数量为2^(h-1)-1,其中h为完全二叉树的高度。因此,该完全二叉树的高度为6,则从根节点到倒数第二层共有2^(6-1)-1=31个节点。又因为最后一层共有8个节点,则该完全二叉树共有31+8=39个节点。因此,答案为选项B:39。
相关文章:

浙大数据结构与算法一些有意思的理论基础题
堆栈 有人给出了堆栈用数组实现的另一种方式,即直接在函数参数中传递数组和top变量(而不是两者组成的结构指针),其中Push操作函数设计如下。这个Push函数正确吗?为什么? #define MaxSize 100 ElementTyp…...

【热门框架】Mybatis-Plus怎样进行映射匹配兼容?Mybatis-Plus的ID有哪些生成策略
Mybatis-Plus提供了两种映射匹配兼容的方式:驼峰转下划线和全局配置。 驼峰转下划线 默认情况下,Mybatis-Plus会将Java类中的驼峰命名方式自动映射到数据库表中的下划线命名方式。例如,Java类中的userName属性会自动映射到表中的user_name字…...

Http1.0 、1.1、2.0、3.0的区别
巨人的肩膀 3.1 HTTP 常见面试题 | 小林coding HTTP1.0与HTTP1.1 HTTP1.1在HTTP1.0上的改进: 使用长连接的方式改善了HTTP1.0中短连接造成的性能开销支持管道网络传输,不必等到上一个的响应,就可以接着发送第二个请求,减少整体响…...

Python——基于YOLOV8的车牌识别(源码+教程)
目录 一、前言 二 、完成效果 三、 项目包 四、运行项目 (教程) 一、前言 YOLOv8LPRNet车牌定位与识别https://www.bilibili.com/video/BV1vk4y1E7MZ/ 最近做了有一个车牌识别的小需求,今天完成了,在此记录和分享 首先&#x…...

c# 数据保存为PDF(一) (spire pdf篇)
文章目录 前言了解 Spire使用Spire.PDF1 创建简单的PDF文档2 创建带有格式的PDF文档(使用Draw)头部信息页眉页脚测试数据完整的代码 3 创建带有格式的PDF文档(使用Gird)小结 先上一个效果图 前言 项目中需要将一些数据转存为PDF …...

Stable Diffusion使用方法
SD的本地安装教程有很多我就不重复了,这里主要是记录我在使用SD Webui的过程中遇到的问题,总结的一些提升出图效率,出好图概率的经验。 先搞几张看看效果 二次元妹妹 高达 ? Ok,以上只是一小部分成品 ,属…...
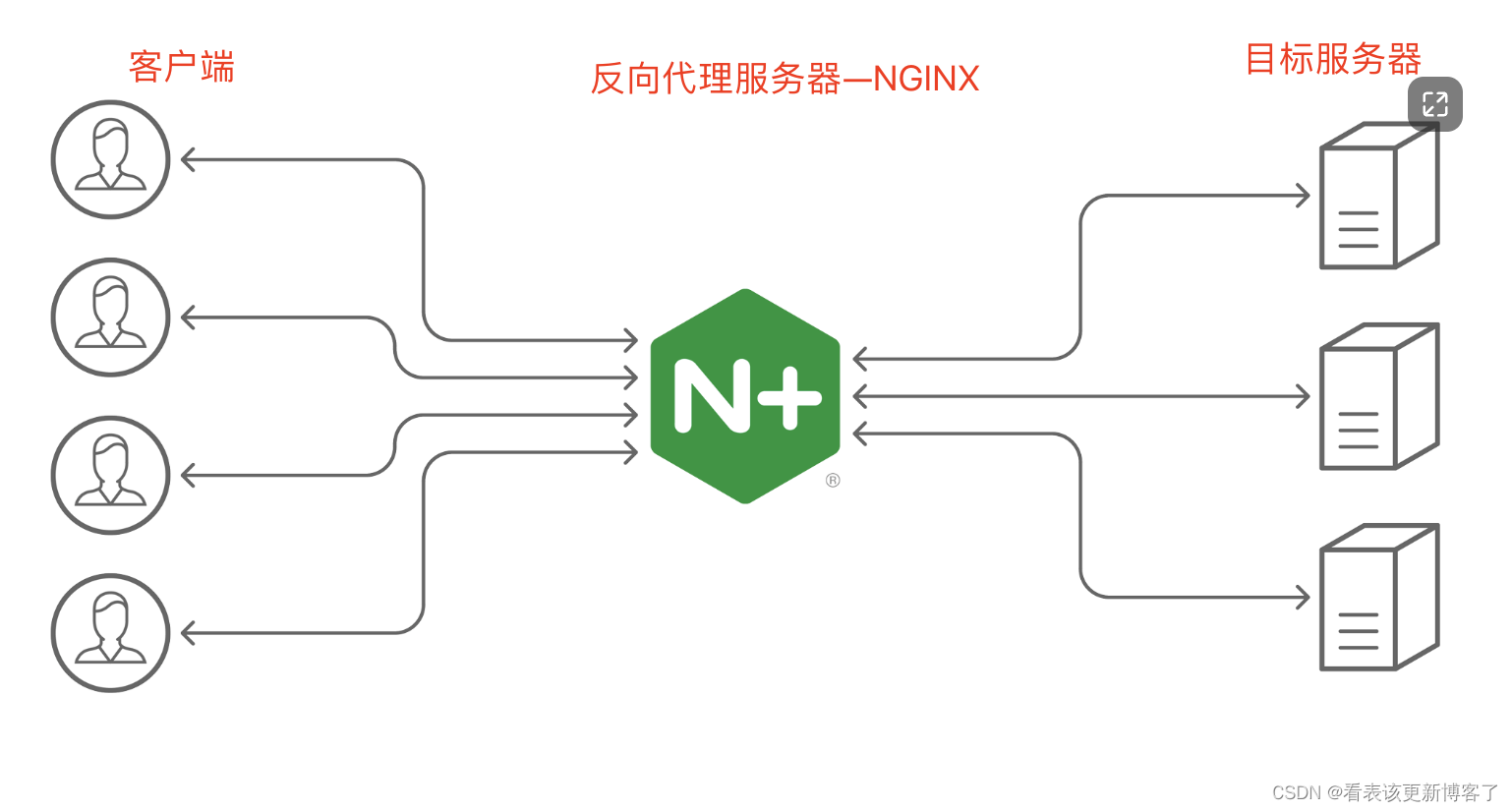
高性能:负载均衡
目录 什么是负载均衡 负载均衡分类 服务端负载均衡 服务端负载均衡——软硬件分类 服务端负载均衡——OSI模型分类 客户端负载均衡 负载均衡常见算法 七层负载均衡做法 DNS解析 反向代理 什么是负载均衡 将用户请求分摊(分流) 到不同的服务器上…...

Matplotlib 安装介绍
文章目录 安装步骤 Matplotlib 不止是一个数学绘图库,它也是可视化和分析工具中最流行之一。我们可用其制作简单的图表,如折线图和散点图。 安装步骤 先进入:python官网 跳转到界面: 录入并搜索 下载之前,看一下自…...

DNS:关于 DNS 基本概念的一些笔记整理
写在前面 分享一些 DNS 的笔记整理博文内容涉及: DNS 历史介绍DNS 解析顺序DNS 基本概念资源类型介绍DNS 安全 理解不足小伙伴帮忙指正 傍晚时分,你坐在屋檐下,看着天慢慢地黑下去,心里寂寞而凄凉,感到自己的生命被剥夺…...

机器人学一些知识
机器人动力学模型是用数学方法描述机器人运动和力学特性的模型。它包含机器人的几何结构、质量、惯性、摩擦等物理特性,以及机器人的控制系统和传感器等。机器人动力学模型可以用于机器人的运动规划、控制算法设计、仿真和优化等应用中。 机器人动力学模型通常采用…...
应用,auto,内联函数
6.引用: //指针 int main() {int a 0;int& b a;int& c b;int& d c;cout << &a << endl;cout << &b << endl;cout << &c << endl;cout << &d << endl;b;d;cout << a <<…...

Flask框架的学习---01
1.工程搭建: (1) 安装flask: pip3 install flask (2)命令行: (1)终端运行:flask run (2)绑定IP地址和端口:Flask run -h 127.0.0.1 -p 8083 修改端口号 (3࿰…...
免费gpt-4-国内使用gpt-4
如何用上gpt-4 GPT-4尚未正式发布和公开,因此我们无法提供对GPT-4的具体使用方法。但是,可以从GPT-4的前一代——GPT-3的使用经验和GPT-4的预期功能来看,建议如下: 了解GPT-4的语言处理能力和适用场景:GPT-4预计将进一…...
《程序员面试金典(第6版)面试题 16.09. 运算
题目描述 请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。 你的实现应该支持如下操作: Operations() 构造函数minus…...

asp.net基于web的校园美食派送配送系统
1.系统登录:系统登录是用户访问系统的路口,设计了系统登录界面,包括用户名、密码和验证码,然后对登录进来的用户判断身份信息,判断是管理员用户还是普通用户。 2.系统用户管理:不管是…...

【JAVA】#详细介绍!!! 文件操作之File对象(1)!
本文内容不涉及文件内容操作,主要是对指定文件元信息的获取,以及通过java代码如何创建一个文件或者删除文件 目录 文件操作的File对象 File对象的基本操作方法 得到文件(夹)对象的信息元 1.getParent 2. getName 3.getPath 4…...

Vue基本的内置指令
前言 除了常见的v-bind,v-for,v-if,v-on.v-model等,本次学习一些vue提供的其他内置指令 1 v-text 给标签插入文本,类似于插值语法 它会把全部的字符串当成文本去解析,不会当成标签的,哪怕写的是标签结构 效果和插值语法是一样的 插值语法比v-text更加…...

华为孟晚舟当值首秀:2030年AI算力将增长500倍!
作者 | 范智林 来源 | 华商观察 微信号:HuashangGC 孟晚舟当值首次亮相。 4月19日,华为副董事长、轮值董事长、CFO孟晚舟在华为第20届全球分析师大会上进行演讲,这是她当值华为轮值董事长以来的首次公开亮相。 按照华为内部规定,…...

关于python异常的总结
Python异常是在程序执行时发生的错误,可能会导致程序终止运行。 在Python中,异常处理是一种机制,它允许开发人员在程序发生异常时捕获、处理和报告这些异常,以便程序可以继续运行或在出现异常时进行优雅的退出。 在Python中&…...
基于Java+SpringBoot+vue学生学习平台详细设计实现
基于JavaSpringBootvue学生学习平台详细设计实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式 文章目…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
