算法记录 | 48 动态规划
198.打家劫舍
思路:
1.确定dp数组(dp table)以及下标的含义:dp[i]:前 i 间房屋所能偷窃到的最高金额。
2.确定递推公式:dp[i] = max(dp[i - 2] + nums[i-1], dp[i - 1])
i间房屋的最后一个房子是nums[i−1]。
如果房屋数大于等于 2 间,则偷窃第 i−1 间房屋的时候,就有两种状态:
-
偷窃第 i−1 间房屋,那么第 i-2 间房屋就不能偷窃了,偷窃的最高金额为:前 i−2 间房屋的最高总金额 + 第 i−1 间房屋的金额,即 dp[i]=dp[i−2]+nums[i-1];
-
不偷窃第 i−1 间房屋,那么第 i−2 间房屋可以偷窃,偷窃的最高金额为:前 i−1 间房屋的最高总金额,即 dp[i]=dp[i−1]。
-
初始条件:
-
前 0 间房屋所能偷窃到的最高金额为 0,即 dp[0]=0。
-
前 1 间房屋所能偷窃到的最高金额为 nums[0],即:dp[1]=nums[0]。
-
-
确定遍历顺序:dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历
class Solution:def rob(self, nums: List[int]) -> int:size = len(nums)if size == 0:return 0dp = [0 for _ in range(size + 1)]dp[0] = 0dp[1] = nums[0]for i in range(2, size + 1):dp[i] = max(dp[i - 2] + nums[i - 1], dp[i - 1])return dp[size]
213.打家劫舍II
思路:
这道题可以看做是「198. 打家劫舍」的升级版。
如果房屋数大于等于 3 间,偷窃了第 1 间房屋,则不能偷窃最后一间房屋。同样偷窃了最后一间房屋则不能偷窃第 1 间房屋。
假设总共房屋数量为size,这种情况可以转换为分别求解 [0,size−2] 和 [1,size−1] 范围下首尾不相连的房屋所能偷窃的最高金额,然后再取这两种情况下的最大值。而求解 [0,size−2] 和 [1,size−1] 范围下首尾不相连的房屋所能偷窃的最高金额问题就跟「198. 打家劫舍」所求问题一致了。
class Solution:def helper(self, nums):size = len(nums)if size == 0:return 0dp = [0 for _ in range(size + 1)]dp[0] = 0dp[1] = nums[0]for i in range(2, size + 1):dp[i] = max(dp[i - 2] + nums[i - 1], dp[i - 1])return dp[size]def rob(self, nums: List[int]) -> int:size = len(nums)if size == 1:return nums[0]ans1 = self.helper(nums[:size - 1])ans2 = self.helper(nums[1:])return max(ans1, ans2)
337.打家劫舍III
思路:
树形动态规划问题。
对于当前节点 cur,不能选择子节点,也不能选择父节点。所以对于一棵子树来说,有两种情况:
- 选择了根节点
- 没有选择根节点
1.选择根节点
如果选择了根节点,则不能再选择左右儿子节点,这种情况下的最大值为:当前节点 + 左子树不选择根节点 + 右子树不选择根节点。
不选择根节点
2.如果不选择根节点,则可以选择左右儿子节点,共四种可能:
- 左子树选择根节点 + 右子树选择根节点
- 左子树选择根节点 + 右子树不选根节点
- 左子树不选根节点 + 右子树选择根节点
- 左子树不选根节点 + 右子树不选根节点
选择其中最大值。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:# dp数组(dp table)以及下标的含义:# 1. 下标为 0 记录 **不偷该节点** 所得到的的最大金钱# 2. 下标为 1 记录 **偷该节点** 所得到的的最大金钱dp = self.traversal(root)return max(dp)# 要用后序遍历, 因为要通过递归函数的返回值来做下一步计算def traversal(self, node):# 递归终止条件,就是遇到了空节点,那肯定是不偷的if not node:return (0, 0)left = self.traversal(node.left)right = self.traversal(node.right)# 不偷当前节点, 偷子节点val_0 = max(left[0], left[1]) + max(right[0], right[1])# 偷当前节点, 不偷子节点val_1 = node.val + left[0] + right[0]return (val_0, val_1)
相关文章:

算法记录 | 48 动态规划
198.打家劫舍 思路: 1.确定dp数组(dp table)以及下标的含义:dp[i]:前 i 间房屋所能偷窃到的最高金额。 2.确定递推公式:dp[i] max(dp[i - 2] nums[i-1], dp[i - 1]) i间房屋的最后一个房子是nums[i−…...

CRM部署Always on 后 CRM报无法更新数据库,数据库只读,且读写分离不正常
CRM部署Always on 后 CRM报无法更新数据库,数据库只读,读写分离不正常 问题描述背景信息问题原因解决方案 问题描述 CRM部署Always on 后 CRM报无法更新数据库,数据库只读 读写分离不正常,出现错乱链接。 背景信息 1.2个节点配置SQL serve…...

麓言信息设计创意思维,打开设计师思路
在现在快速发展的时代,信息纷杂繁琐,如果一个设计不能让人眼前一亮,印象深刻,只会沦为平凡作品,无亮点无用处。正所谓,无设计不创意,这句口号正是喊出对设计的要求。 伴随着时代的发展、…...

POJ3704 括号匹配问题 递归方法
目录 题目 算法 完整代码 题目 参考 递归: https://blog.csdn.net/qq_45272251/article/details/103257953 利用了递归, 但思路稍复杂了 循环: https://blog.csdn.net/weixin_50340097/article/details/114579805 (看起来是递归其实是循环. 每次递归其实是循环内一次迭…...
:完全相等的 JSON 字符串、复合函数、 分组、柯里化、将对象转换为 JSON 字符串)
leetcode — JavaScript专题(三):完全相等的 JSON 字符串、复合函数、 分组、柯里化、将对象转换为 JSON 字符串
专栏声明:只求用最简单的,容易理解的方法通过,不求优化,不喜勿喷 2628. 完全相等的 JSON 字符串 题面 给定两个对象 o1 和 o2 ,请你检查它们是否 完全相等 。 对于两个 完全相等 的对象,它们必须包含相…...

OGNL 的表达式
目录 概念 基本原理 基本语法 1、访问Root区域对象基本语法 2、访问Context区域对象基本语法 符号含义 概念 Object-Graph Navigation Language 对象-图形导航语言, 主要用于访问对象的数据和方法。 基本原理 主要由3部分构成:1.OGNL引擎 …...

JAVA面试中遇到的那些坑,80%的人都种过招
面试,是很多学完Java开发的人不得不面对的问题。小编经常听到学员抱怨,明明觉得自己学的不错,为什么到了面试的时候就凉凉了?为什么有的面试官会一直问业务层面的问题,让人措手不及? 其实,我们在学习Java知识的同时…...

【测试开发】单元测试、基准测试和性能分析(以 Go testing 为例)
一、为什么需要测试🤔️ 你写不出 bug-free 的代码。你认为自己写出了 bug-free 的代码,但它在你意想不到的地方出错了。你觉得自己写出了永不出错的代码,但它的性能十分糟糕。 二、在开发过程中做好测试(理想情况下)…...

linux中一条命令查询当前端口的进程,然后拿到进程pid,作为另一条杀死进程的参数
1. 可以使用lsof命令来查询端口对应的进程,然后使用awk命令提取PID,最后将其作为另一条命令的参数。 例如,如果要查询端口为8080的进程: lsof -i :8080 | awk NR2{print $2}其中,-i选项指定查询网络连接,…...

程序员找工作难吗?我用亲身经历来告诉大家
我看到很多同学说今年的程序员找工作难。我的心里也有一定预期,但直到我出来之后才真正地感受到这股寒冬有多么凛冽。 一个外包公司有四五个招聘人员,然后外包公司有十来个,一个公司的岗位会分发给这些各个不同的外包公司。所以你看到我沟通…...
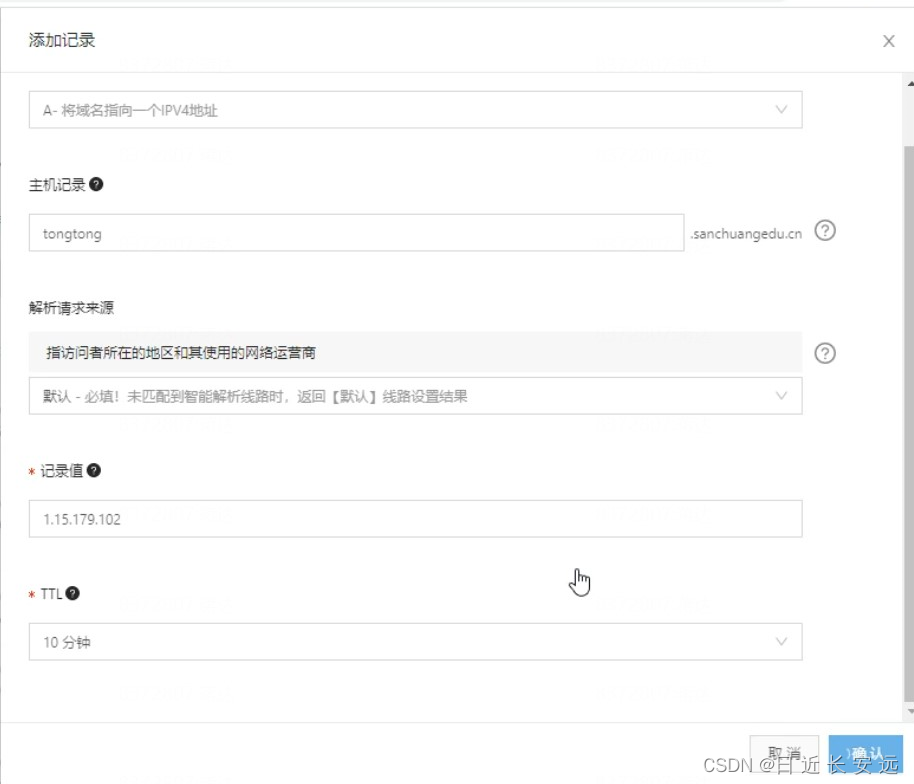
【Web服务】HTTP和DNS重要知识
304状态码 HTTP状态码中的304状态码表示"未修改",通常在客户端发起了一个带有If-Modified-Since头部的GET请求时会得到这个响应。服务器通过比较If-Modified-Since头部指定的时间戳和资源的最后修改时间来判断资源是否被修改过,如果没有修改则…...

【C++】-关于类和对象的默认成员函数(中)-拷贝构造函数和赋值运算符重载函数
💖作者:小树苗渴望变成参天大树 ❤️🩹作者宣言:认真写好每一篇博客 💨作者gitee:gitee 💞作者专栏:C语言,数据结构初阶,Linux,C 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点…...
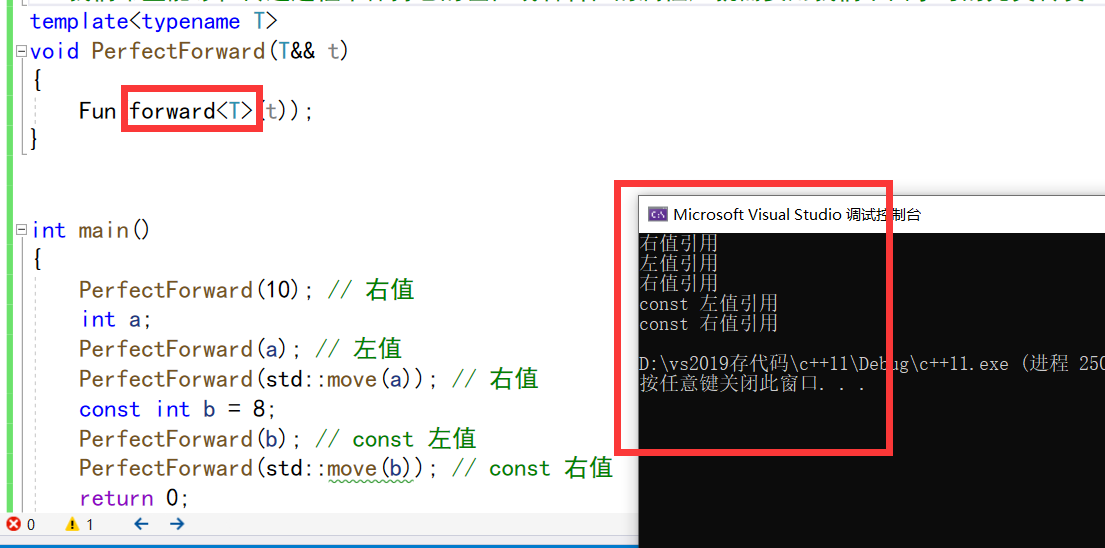
c++11上篇
c11 1.C11简介2.列表初始化2.1 {}初始化2.2 std::initializer_list 3.变量类型推导3.1 auto3.2 decltype3.3 nullptr 4.范围for循环5.final与override6.智能指针7.新增加容器---静态数组array、forward_list以及unordered系列8.默认成员函数控制9.右值引…...
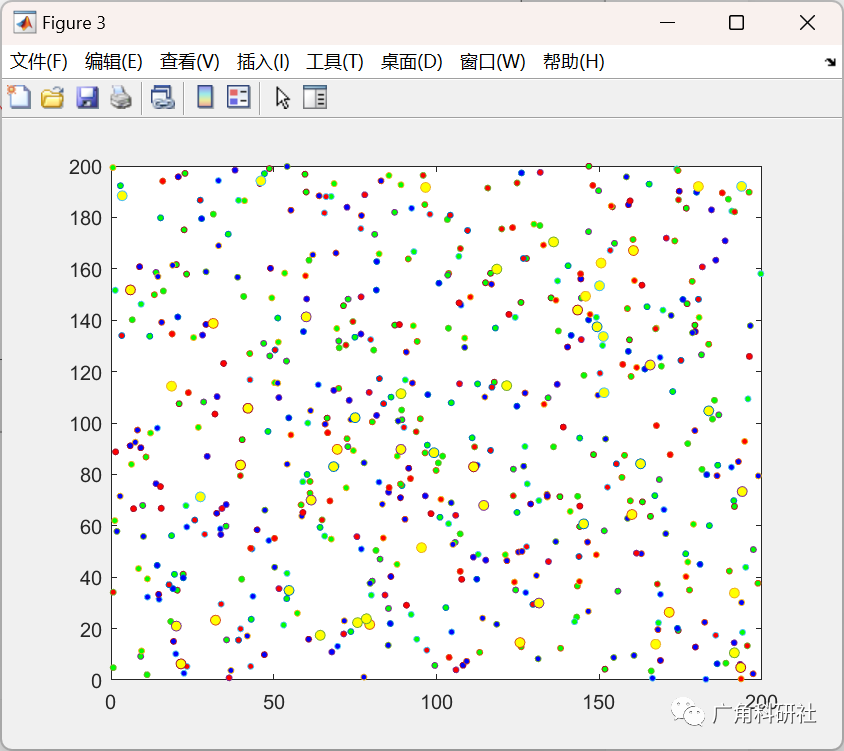
异构无线传感器网络路由算法研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 无线传感器网络(Wireless Sensor Networks, WSN)是一种新型的融合传感器、计算机、通信等多学科的信息获取和处理技术的网络,…...

MySQL数据库——MySQL TRUNCATE:清空表记录
MySQL 提供了 DELETE 和 TRUNCATE 关键字来删除表中的数据。下面主要讲解一下 TRUNCATE 关键字的使用。 TRUNCATE 关键字用于完全清空一个表。其语法格式如下: TRUNCATE [TABLE] 表名 其中,TABLE 关键字可省略。 例 1 新建表 tb_student_course&…...

财报解读:连续三年逆势增长的背后,欧派家居到底靠的是什么?
能在过去3年逆势增长的家居企业并不多,而欧派家居就是其中一个。4月25日,欧派家居发布2022年年度报告。据年报数据显示,2022年,欧派家居共实现营业收入224.80亿元,净利润约26.88亿元。 从2020年到2022年,欧…...

希望计算机专业同学都知道这些宝藏博主
湖科大教书匠——计算机网络 “宝藏老师”、“干货满满”、“羡慕湖科大”…这些都是网友对这门网课的评价,可见网课质量之高! 湖南科技大学《计算机网络》微课堂是该校高军老师精心制作的视频课程,用简单的语言描述复杂的问题,…...
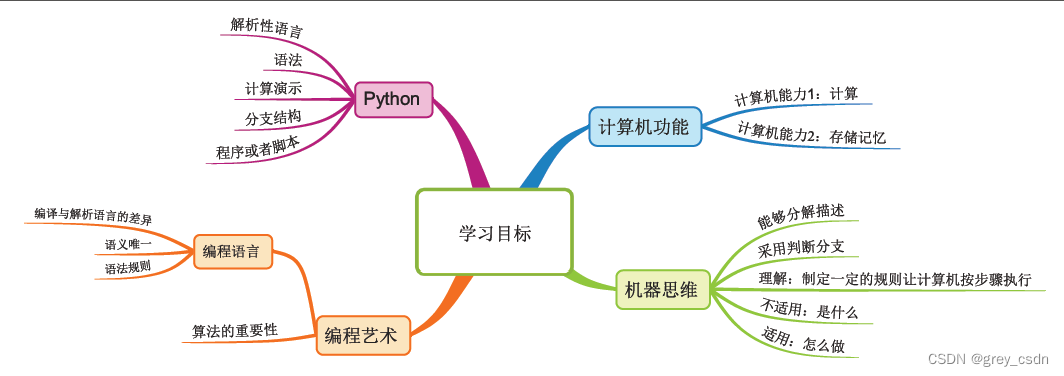
1694_week1_MIT使用Python编程学习手记1
全部学习汇总: GreyZhang/python_basic: My learning notes about python. (github.com) 首先说明一下,这部分信息的整理只是我个人的理解。由于自己的知识功底以及英语水准,很可能会有大量的疏漏。再此,我只想把自己学习时候的一…...
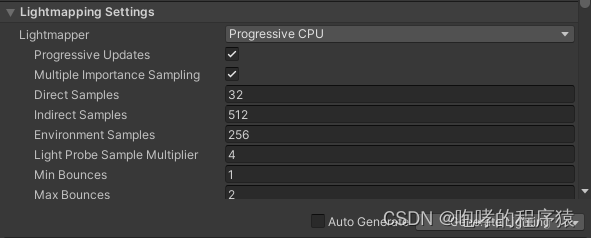
第二十一章 光源
光源是每个场景必不可少的部分,光源除了能够照亮场景之外,还可以产生阴影效果。 Unity中分为四种光源类型: 1. 方向光:Directional Light 用于模拟太阳光,方向光任何地方都能照射到。 2. 点光源:Point L…...
方向上接收论文总结)
CVPR 2023 超分辨率(super-resolution)方向上接收论文总结
目录 CVPR 2023图像超分任意尺度超分盲超分 视频超分特殊场景 总结参考资料 CVPR 2023 官网链接:https://cvpr2023.thecvf.com/ 会议时间:2023年6月18日-6月22日,加拿大温哥华 CVPR 2023统计数据: 提交:9155篇论文接…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
