数据结构刷题(三十):96不同的二叉搜索树、01背包问题理论、416分割等和子集
一、96. 不同的二叉搜索树
1.这个题比较难想递推公式,
dp[3],就是元素1为头结点搜索树的数量 + 元素2为头结点BFS的数量 + 元素3为头结点BFS的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
用公式来说明就是
i>= 2, dp[i] += dp[p - 1] + dp[i - p]
2.需要注意dp数组的初始化
代码:
class Solution {public int numTrees(int n) {// 初始化int[] dp = new int[n + 1];// 分别初始化节点为0和1时的情况dp[0] = 1;dp[1] = 1;// 讨论j作为根结点时的情况 从左侧dp[0]到右侧dp[0]for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++){//对于第i个节点,需要考虑1作为根节点直到i作为根节点的情况,所以需要累加dp[i] += dp[j - 1] * dp[i - j] ;}}return dp[n];}
}二、01背包问题理论

dp[i][j]是在背包达到j重量时,任取0-i中任意多个物品,所达到的最大价值, 其中i代表物品,j代表背包容量; 现在需要放入i物品到背包中,需要对比不放物品i和放入物品i两种情况。
- 不放物品i:直接就是dp[i-1][j]的最有情况
- 放入物品i:确定放入i时,则整个物品集就被分成两部分,1到i-1和第i个,同时物品i会把j空间里的wi给占据了,只剩下j-wi的空间给前面i-1, 所以dp[i-1][j-weight[i]]的意思就是还没加上物品i的重量(weight[i])时的最大价值, 最后再加上i物品的价值
细节:1.当 j-weight【i】<0 时,数组会越界,要加个if j<weight【i】则 dp【i】【j】=dp【i-1】【j】;
2.初始化时,当背包容量j=0时,不论i等于几,都默认为0;而i=0时,可以根据物品i=0的重量设定初始值。
3.当dp是二维数组时,双层for循环是可以颠倒顺序的
三、01背包问题理论(二)
1.将二维数组转换成一维的滚动数组
2.dp[j]指的是容量为j时的最大价值
3.列表后面的值需要通过与前面的值(可能在第一次循环中就确定了dp[1]的值,只能使用倒序才能获取到最开始的dp[1],而不是使用正序去更新dp[1])比较确定,因此要先处理,所以在嵌套for循环需要使用倒序

四、416. 分割等和子集
1.使用01背包思想,以下四点是使用01背包解决这个题的要求:
- 背包的体积为sum / 2。(已知体积)
- 背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。(满足01背包要求)
2.需要注意本题中的重量也就是价值这一说法
(1)01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
(2)如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j
class Solution {public boolean canPartition(int[] nums) {if (nums.length == 0 && nums == null)return false;int n = nums.length;int sum = 0;for (int num : nums) {sum += num;}// 判断和是否为奇数if (sum % 2 == 1) return false;int target = sum / 2;// dp[j]表示 当背包重量为j时,所具有的最大价值(这个题价值也就是重量)int[] dp = new int[target + 1];for (int i = 0; i < n; i++) {for (int j = target; j >= nums[i]; j--){//物品 i 的重量是 nums[i],其价值也是 nums[i]dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}// 只需要对两个子集中的一个进行判断即可,return dp[target] == target;}
}相关文章:

数据结构刷题(三十):96不同的二叉搜索树、01背包问题理论、416分割等和子集
一、96. 不同的二叉搜索树 1.这个题比较难想递推公式, dp[3],就是元素1为头结点搜索树的数量 元素2为头结点BFS的数量 元素3为头结点BFS的数量 元素1为头结点搜索树的数量 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量 元素2为头结…...

bash的进程与欢迎讯息自定义
在bash shell中,可以通过多种方式自定义欢迎讯息和提示符。主要有: 修改/etc/profile文件: 该文件在用户登录后执行,定义了PROMPT_COMMAND和PS1提示符。可以修改其内容实现自定义欢迎讯息和提示符。 例如,修改为: bash PROMPT_COMMANDecho -e "\nWelcome to My Bash She…...

本周大新闻|苹果首款MR没有主打卖点;Meta认为AI是AR OS的基础
本周XR大新闻,AR方面,苹果首款MR或没有主打卖点,反而尽可能支持更多App和服务;扎克伯格表示基于AI的AR眼镜操作系统是下一代计算平台的基础;微软芯片工程VP Jean Boufarhat加入Meta芯片团队;Humane展示了…...

Java中工具类Arrays、Collections、Objects
Arrays Arrays是Java中提供的一个针对数组操作的工具类,所有的方法都是静态的。 大致有这些常用的方法 sort()针对常用的基本数据类型,都能进行排序,byte、char、int、long、float、doubleparallelSort()并行排序,多线程排序&am…...

Docker安装Nginx/Python/Golang/Vscode【亲测可用】
一、docker安装nginx docker安装nginx,安装的是最新版本的:docker pull nginx:latest 创建一个容器:docker run --name my-nginx -p 80:80 -d nginx:latest 开启一个交互模式终端:docker exec -it my-nginx bash 创建django项…...

蓝桥杯2022年第十三届决赛真题-最大数字
蓝桥杯2022年第十三届决赛真题-最大数字 时间限制: 3s 内存限制: 320MB 题目描述 给定一个正整数 N。你可以对 N 的任意一位数字执行任意次以下 2 种操作: 将该位数字加 1。如果该位数字已经是 9,加 1 之后变成 0。 将该位数字减 1。如果该位数字已经…...
smbms项目搭建
目录 1.搭建一个maven web项目 2.配置Tomcat 3.测试项目是否能够跑起来 4.导入项目中会遇到的Jar包 5.项目结构搭建 6.项目实体类搭建 7.编写基础公共类 1.数据库配置文件 2.编写数据库的公共类 3.编写字符编码过滤器 3.1web配置注册 4.导入静态资源 1.搭建一个maven web项目 …...
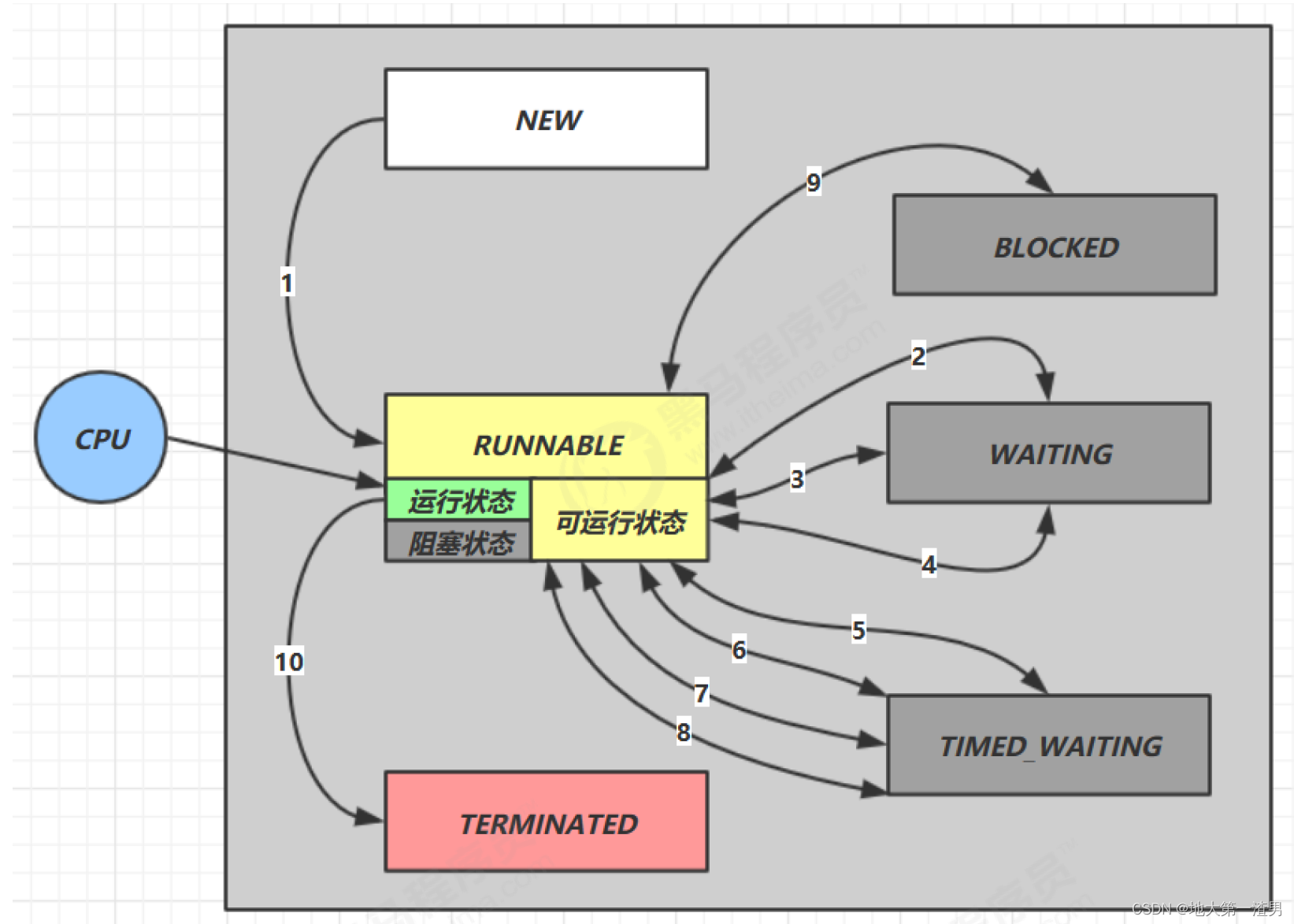
进程/线程 状态模型详解
前言:最近操作系统复习到线程的状态模型(也可以说进程的状态模型,本文直接用线程来说)时候,网上查阅资料,发现很多文章都说的很不一样,有五状态模型、六状态模型、七状态模型.......虽然都是对的…...
)
数据结构与算法之队列: Leetcode 621. 任务调度器 (Typescript版)
任务调度器 https://leetcode.cn/problems/task-scheduler/ 描述 给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间&#…...
【报错】arXiv上传文章出现XXX.sty not found
笔者在overleaf上编译文章一切正常,但上传文章到arxiv时出现类似于如下报错: 一般情况下观察arxiv的编译log,不通过的原因,很多时候都是由于某一行导入了啥package,引起的报错;但是如果没有任何一个具体的…...

项目合同管理
项目合同管理的基本概念及分类、项目合同签订、项目合同管理以及项目合同索赔处理等内容 信息系统工程的建设过程实际上就是合同的执行和监控的过程 1、项目合同的概念及分类 合同法律关系:权力和义务关系 合同可以是书面形式、口头形式和其他形式 书面形式是指…...

聊聊ClickHouse向量化执行引擎-过滤操作
俄罗斯Yandex开发的ClickHouse是一款性能黑马的OLAP数据库,其对SIMD的灵活运用给其带来了难以置信的性能。本文我们聊聊它如何对过滤操作进行SIMD优化。 基本思想 1、有一个数组data,即ColumnVector::data,存放数据 2、使用uint8类型…...
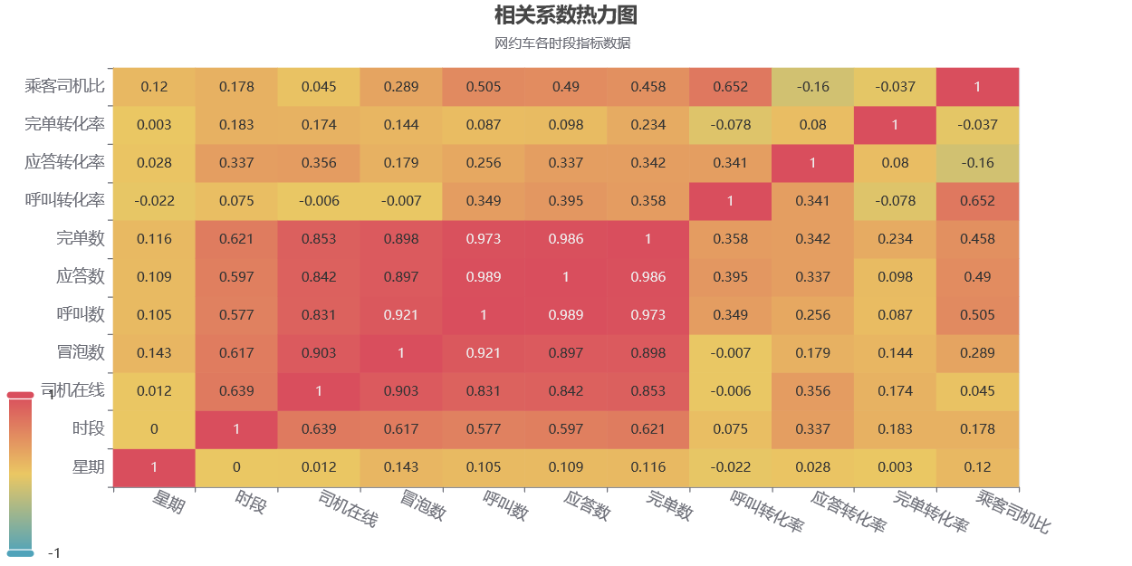
数据可视化第二版-拓展-网约车分析案例
文章目录 数据可视化第二版-拓展-网约车分析案例竞赛介绍 1等奖作品-IT从业者张某某的作品结论过程数据和思考数据处理数据探索数据分析方法选择数据分析相关性分析转化率分析分析结论 完单数量分析分析结论 司机数量分析分析结论 时间分析每日订单分析 工作日各时段分析周六日…...
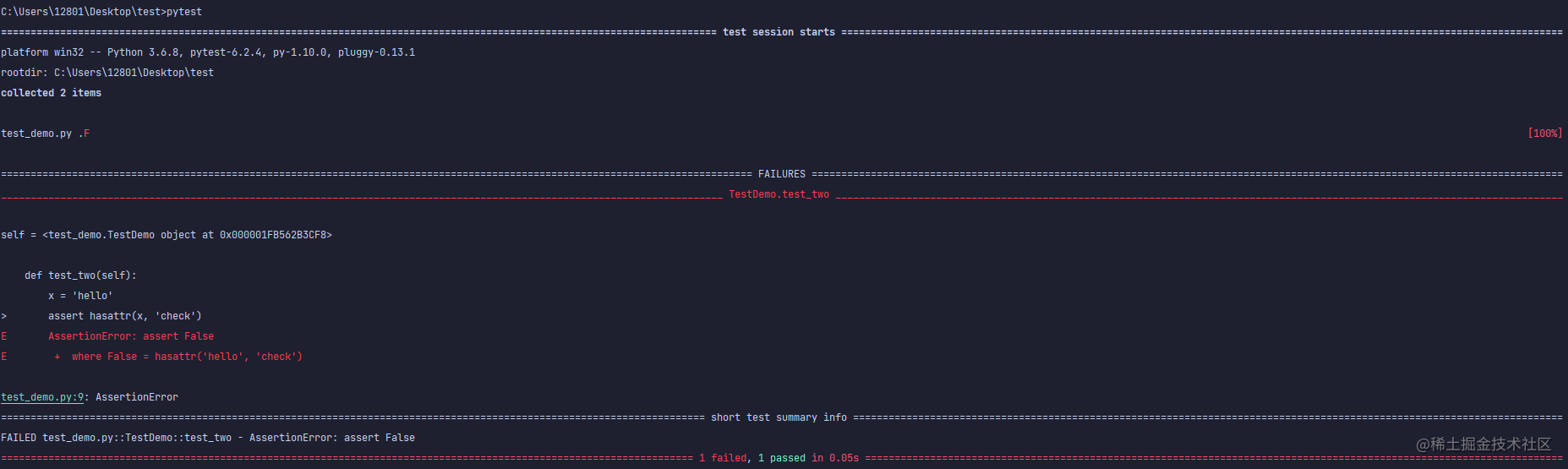
pytest - Getting Start
前言 项目开发中有很多的功能,通常开发人员需要对自己编写的代码进行自测,除了借助postman等工具进行测试外,还需要编写单元测试对开发的代码进行测试,通过单元测试来判断代码是否能够实现需求,本文介绍的pytest模块是…...
( 字符串) 205. 同构字符串 ——【Leetcode每日一题】
❓205. 同构字符串 难度:简单 给定两个字符串 s 和 t ,判断它们是否是同构的。 如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。 每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同…...
python+django+vue消防知识宣传网站
开发语言:Python 框架:django Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat 开发软件:PyCharm 层随着移动应用技术的发展,越来越多的消防单位借助于移动手机、电脑完成生活中的事…...

彻底告别手动配置任务,魔改xxl-job!
分析 改造 1、接口调用 2、创建新注解 3、自动注册核心 4、自动装配 测试 测试后 XXL-Job是一款非常优秀的任务调度中间件,其轻量级、使用简单、支持分布式等优点,被广泛应用在我们的项目中,解决了不少定时任务的调度问题。不仅如此&a…...

【五一创作】Springboot+多环境+多数据源(MySQL+Phoenix)配置及查询(多知识点)
文章目录 1. 背景2. 技术点3 子模块依赖SpringBoot设置4. 多环境配置4.1 application.yml4.2 application-pro.yml 5. 多数据源配置5.1 yml配置5.2 自定义数据源在Java中配置5.2.1 PhoenixDataSourceConfig5.2.2 MysqlDataSourceConfig 6. 完整的Pom6. 测试6.1 Mapper配置6.2 方…...

Python小姿势 - 线程和进程:
线程和进程: Python里面线程是真正的并行执行,进程是可以并行执行的。 所谓进程,就是操作系统中执行一个程序的独立单元,它是系统进行资源分配和调度的基本单位。一个进程可以创建和撤销另一个进程,同一个进程内可以并…...
Mysql 锁
目录 0 课程视频 1 概述 1.1 多用户 并发访问 -> 为了数据一致性(多用户) 1.2 全局锁 数据库所有表 1.3 表级锁 每次操作 锁整张表 1.4 行级锁 每次操作 锁对应行 2 全局锁 ->锁后只读 -> 全库逻辑备份 2.1 阻塞DML /DDL 可DQL读 2.2 语法 2.2.1 加锁 flush…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
