OJ刷题 第十四篇(递归较多)
23204 - 进制转换
时间限制 : 1 秒
内存限制 : 128 MB
将一个10进制数x(1 <= x <= 100,000,000)转换成m进制数(2<= m <= 16) 。分别用 ABCDEF表示10以上的数字。
输入
x m (1 <= x <= 100,000,000, 2<= m <= 16)
输出
m进制数
样例
输入
31 16
输出
1F
答案:
#include<iostream>
using namespace std;
int main() {int x, m;cin >> x >> m;char arr[17] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};char s[32] = { 0 };int length = 0;while (x) {int r = x % m;s[length++] = arr[r];x /= m;}for (int i = length - 1; i >= 0; i--) {cout << s[i];}return 0;
}分析:这道题在刚学C语言或者数据结构栈那里来写是比较难的,因为栈的一个应用就是可以用来求进制转换。由于这道题是2到16进制之间任意进制的转换,因此我们要定义一个数组用来表示每次取模后的字符。并初始化,比如本题中的arr数组,先递增存储,最后倒着打印即可。
本题难的地方就是构造那个arr数组用来存储每次取模后的的字符。最后要倒着打印,刚开始学C语言感觉这题很难,但是现在感觉就基础题!
是否通过:
31001 - 数字三角形(动态规划思想)
时间限制 : 1 秒
内存限制 : 128 MB
如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
- 一步可沿左斜线向下或右斜线向下走;
- 三角形行数小于等于100;
- 三角形中的数字为0,1,…,99。
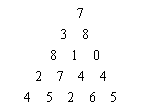
输入
测试数据通过键盘逐行输入
输出
最大值
样例
输入
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
输出
30
答案:
#include<iostream>
using namespace std;
int main() {int n;int a[101][101] = { 0 };cin >> n;//输入数据,从下标1开始,对本题计算大有帮助for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}//计算for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {int max1 = a[i][j] + a[i - 1][j - 1];int max2 = a[i][j] + a[i - 1][j];int max = max1 > max2 ? max1 : max2;a[i][j] = max;}}//找最大值路径int MAX = a[n][1];for (int i = 2; i <= n; i++) {MAX = MAX > a[n][i] ? MAX : a[n][i];}cout << MAX << endl;return 0;
}分析:这个题其实难度不算大,只是题目有点难度的思维逻辑。题目说到:
一步可沿左斜线向下或右斜线向下走
这个是什么意思呢?意思就是说对每个元素a[i][j],到这个元素的路径只能从两个地方得来:
1、加上a[i-1][j-1],得到一个路径值
2、加上a[i-1][j],得到一个路径值
每个点都只有这两种情况,然后选出值较大的那个作为这个点的路径值。直到算到最后一行,然后找出最后一行的最大值即可。
是否通过:
31002 - 走楼梯
时间限制 : 1 秒
内存限制 : 128 MB
楼梯有 N 级台阶,上楼可以一步上一阶,也可以一步上二阶。编一递归程序,计算共有多少种不同走法?
输入
一个整数,表示 N 级台阶
输出
整数,表示走法的数量
样例
输入
3
输出
3
答案:
#include<iostream>
using namespace std;
int f1(int N) {if (N == 1) {return 1;}if (N == 2) {return 2;}return f1(N - 2) + f1(N - 1);
}
int main() {int N;cin >> N;int count = f1(N);cout << count << endl;return 0;
}分析:这是初学C语言遇到的最多的问题,也是一个非常经典的问题。它的核心思想就是
f3=f1+f2
一般能不用递归就不用,因为递归会消耗栈,问题规模大了,会重复计算很多,浪费时间。
是否通过:
31003 - 兔子繁殖
时间限制 : 1 秒
内存限制 : 128 MB
有一种兔子,出生后一个月就可以长大,然后再过一个月一对长大的兔子就可以生育一对小兔子且以后每个月都能生育一对。现在,我们有一对刚出生的这种兔子,那么,n 个月过后,我们会有多少对兔子呢?假设所有的兔子都不会死亡。
输入
输入文件仅一行,包含一个自然数 n。
输出
输出文件仅一行,包含一个自然数,即 n 个月后兔子的对数。
样例
输入
5
输出
5
#include<iostream>
using namespace std;
int main() {int n;cin >> n;long long sum = 0;if (n == 1 || n == 2) {sum = 1;}else {long long int f1 = 1, f2 = 1;for (int i = 3; i <= n; i++) {sum = f1 + f2;f2 = f1;f1 = sum;}}cout << sum << endl;return 0;
}分析:兔子繁殖问题就是一个著名的斐波那契数列。同样可以用递归,但是这里我没有用递归,性能会大幅度提高。
是否通过:
31004 - 骨牌铺法 (进阶版递归,二刷!!)
时间限制 : 1 秒
内存限制 : 128 MB
有 1×n 的一个长方形,用一个 1×1、1×2 和 1×3 的骨牌铺满方格。例如当 n=3 时为 1×3 的方格。
此时用 1×1、1×2 和 1×3 的骨牌铺满方格,共有四种铺法。如下图:

输入
n
输出
一共有多少种铺法
样例
输入
3
输出
4
答案:
#include<iostream>
using namespace std;int main() {int n;cin >> n;int sum = 0;if (n == 1) {sum = 1;}else if (n == 2) {sum = 2;}else if (n == 3) {sum = 4;}else {int f1 = 1, f2 = 2, f3 = 4;for (int i = 4; i <= n; i++) {sum = f1 + f2 + f3;f1 = f2;f2 = f3;f3 = sum;}}cout << sum << endl;return 0;
}分析:这个题第一次遇到感觉难度非常大,一是觉得题目生疏很难,或者说没理解题目的意思。我们先来整理题目的意思,当然我们知道
如果是1*1的矩形,只有 1种填充方法
如果是1*2的矩形,有2种填充方法,一种是全部用1*1方形填充,一种是一个用1*2方形填充
如果是1*3的矩形,有4种填充,怎么算?一种是全部用1*1的填充,一种是前面一个位置用1*1的方形填充,后面两个位置用1*2的方形填充,一种是前面两个位置用1*2的填充,后面一个位置用1*1的填充,最后一种就是直接用1*3的填充。
如果是1*4的矩阵,那么第一个位置用1*1的方形填充,后面三个位置任意填充有4种,前面两个位置用1*2的方形填充,后面两个位置有2种,前面三个位置用1*3的方形填充,后面一个位置有1种,即公有1+2+4=7种。
我想到这里已经发现了,骨牌铺法也是一个递归问题,相比斐波那契数列,这个题深度更深
f4=f3+f2+f1
是否通过:

23207 - 五子棋(重点!!二刷!)
时间限制 : 1 秒
内存限制 : 128 MB
五子棋是世界智力运动会竞技项目之一,是一种两人对弈的纯策略型棋类游戏,通常双方分别使用黑白两色的棋子,下在棋盘直线与横线的交叉点上,先形成5子连线者获胜。如果要开发一款五子棋小游戏,判断棋局输赢也将是其中很重要的一部分。
现有一个n行m列的棋盘,我们使用1表示棋格里有黑色棋子,2表示棋格里有白色棋子,0表示没有棋子。 给定t场对弈棋局,请判断是否有5子连线的棋子,如果有则输出Yes,没有则输出No。
输入
第1行,n m t (1≤n、m≤100,1≤t≤10) 接下来共t组数据,每行组数据n行,每行m个整数,每个整数的取值为0、1或者2
输出
t 行,如果有5子连线的棋子则输出Yes,否则输出No。每行一个。
样例
输入
5 6 4 1 1 1 1 1 0 2 2 0 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 02 1 1 0 1 0 2 1 0 2 2 0 0 1 0 2 0 0 0 1 0 2 0 0 0 1 0 2 0 02 1 1 0 1 0 0 2 0 2 2 0 0 1 0 1 0 0 0 0 0 2 0 0 0 1 0 2 0 12 1 1 0 1 2 2 1 0 2 2 0 0 1 0 2 0 0 0 1 2 2 0 0 0 2 0 2 0 0
输出
Yes Yes No Yes
答案:
#include<iostream>
using namespace std;
bool Check(int a[][200], int n, int m) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (a[i][j] != 0) {//判断右横if (j + 4 <= m &&a[i][j] == a[i][j+1] &&a[i][j] == a[i][j+2] &&a[i][j] == a[i][j+3] &&a[i][j] == a[i][j+4]) {return true;}//判断下竖if (i + 4 <= n &&a[i][j] == a[i+1][j] &&a[i][j] == a[i+2][j] &&a[i][j] == a[i+3][j] &&a[i][j] == a[i+4][j]) {return true;}//判断右斜if (j + 4 <= m && i + 4 <= n &&a[i][j] == a[i+1][j+1] &&a[i][j] == a[i+2][j+2] &&a[i][j] == a[i+3][j+3] &&a[i][j] == a[i+4][j+4]) {return true;}//判断左斜if (j >= 5 && i + 4 <= n &&a[i][j] == a[i+1][j-1] &&a[i][j] == a[i+2][j-2] &&a[i][j] == a[i+3][j-3] &&a[i][j] == a[i+4][j-4]) {return true;} }}}return false;
}
int main() {int n, m, t;int a[200][200];cin >> n >> m >> t;for (int k = 1; k <= t; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> a[i][j];}}if (Check(a, n, m)) {cout << "Yes" << endl;}else {cout << "No" << endl;}}
}分析:虽然很多人下过五子棋也知道下棋规则,但是要写代码判断一个棋局是不是分出胜负还是有不小难度的。五子棋游戏这是一款经典游戏,之前也开发来玩过。我们在判断的时候不用判断所有棋子,我们只需判断部分棋子就可以知道胜负,分四种情况:
1、右横,即某一行有5个棋子即可,只需判断最后一个棋子不超过棋盘的列数即可,即j+4<=m
2、下竖,即某一列有5个棋子即可,只需判断最后一个棋子的行数不超过棋盘的行数即可,即i+4<=n
3、右斜,即主对角线方向有5个棋子,两个条件,因为是斜着向右下方,因此j+4<=m且i+4<=n
4、左斜,即副对角线方向有5个棋子,同样是两个条件,因为是斜着向左下方,因此i+4<=n且j-4>=1,即只需j>=5即可!
是否通过:
相关文章:

OJ刷题 第十四篇(递归较多)
23204 - 进制转换 时间限制 : 1 秒 内存限制 : 128 MB 将一个10进制数x(1 < x < 100,000,000)转换成m进制数(2< m < 16) 。分别用 ABCDEF表示10以上的数字。 输入 x m (1 < x < 100,000,000, 2< m < 16) 输出 m进制数 样例 输入 31 16 输出 1F 答…...
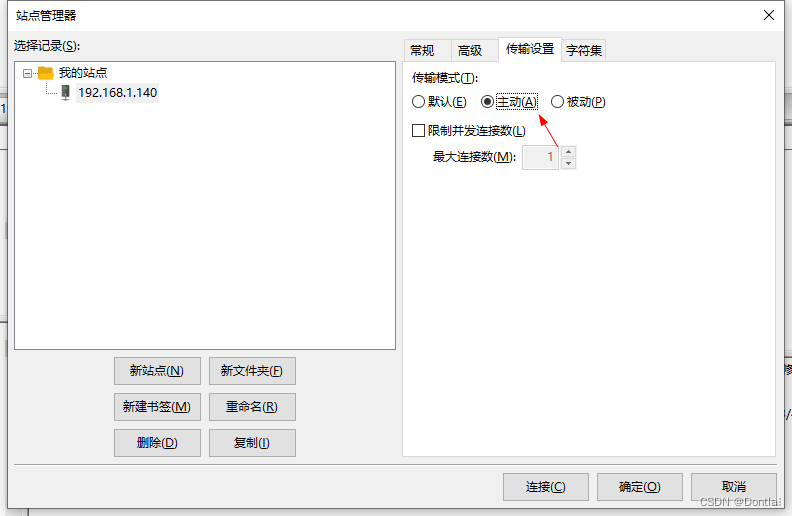
FileZilla读取目录列表失败(vsftpd被动模式passive mode部署不正确)
文章目录 现象问题原因解决方法临时解决(将默认连接方式改成主动模式)从根本解决(正确部署vsftpd的被动模式) 现象 用FileZilla快速连接vsftpd服务器时,提示读取目录列表失败 问题原因 是我vsftpd服务端的被动模式没…...
【Java面试八股文】数据库篇
导航: 【黑马Java笔记踩坑汇总】JavaSEJavaWebSSMSpringBoot瑞吉外卖SpringCloud黑马旅游谷粒商城学成在线MySQL高级篇设计模式牛客面试题 目录 请你说说MySQL索引,以及它们的好处和坏处 请你说说MySQL的索引是什么结构,为什么不用哈希表 请你说说数据库索引的底…...

Android Glide加载图片、网络监听、设置资源监听
再搞事情之前首先创建一个项目,就命名为GlideDemo吧。 一、项目配置 创建好之后,在app模块下build.gradle的dependencies闭包中添加如下依赖: //glide//glideimplementation com.github.bumptech.glide:glide:4.11.0annotationProcess…...

等保定级报告模版
等保定级怎么做_luozhonghua2000的博客-CSDN博客 上篇给大家说清楚了,等保定级怎么做,但在日常工作中,需要向上级或甲方输出定级报告,这篇我降弄个模版供大家参考。 信息系统安全等级保护定级报告 XX 平台系统描述 (一) 2023年5月,XX 正式上线,XX 隶属于深圳 XX 科技…...

计算机组成原理4.2.2汉明码
编码的最小距离 奇校验和偶校验 看1的个数是奇数 还是偶数 汉明码 汉明码的配置 根据不等式,确定增添几位,根据指数放置增添位 汉明码的检错 分不同检测小组 分组规则:哪位为’1‘就是哪组元素。 1号位为‘1’的都是第一组元素&#…...

JavaScript全解析——本地存储的概念、用法详解
本地存储概念: 就是浏览器给我们提供的可以让我们在浏览器上保存一些数据 常用的本地存储 localStorage sessionStorage localStorage 特点: 1.长期存储,除非手动删除否则会一直保存在浏览器中,清除缓存或者卸载浏览器也就没有了 2.可以跨页面通讯,…...
对象浅拷贝的5种方式
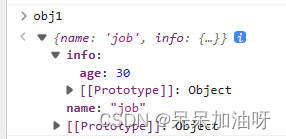
参考原文:浅拷贝的五种实现方式 - 掘金 (juejin.cn) 哈喽 大家好啊 最近发现自己对对象都不是很熟练,特别是涉及到一些复制,深浅拷贝的东西 1.Object.assign 首先 我们创建一个空对象obj1 然后创建一个对象obj2 用object.assign(目标对象,…...

Java每日一练(20230504)
目录 1. 位1的个数 🌟 2. 移除元素 🌟 3. 验证二叉搜索树 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 位1的个数 编写一个…...

【深度学习】计算机视觉(13)——模型评价及结果记录
1 Tensorboard怎么解读? 因为意识到tensorboard的使用远不止画个图放个图片那么简单,所以这里总结一些关键知识的笔记。由于时间问题,我先学习目前使用最多的功能,大部分源码都包含summary的具体使用,基本不需要自己修…...

项目经理在项目中是什么角色?
有人说,项目经理就是一个求人的差事,你是在求人帮你做事。 有人说,项目经理就是一个与人扯皮的差事,你要不断的与开发、产品、测试等之间沟通、协调。 确实,在做项目的时候,有的人是为了完成功能&#x…...

【技术分享】防止根据IP查域名,防止源站IP泄露
有的人设置了禁止 IP 访问网站,但是别人用 https://ip 的形式,会跳到你服务器所绑定的一个域名网站上 直接通过 https://IP, 访问网站,会出现“您的连接不是私密连接”,然后点高级,会出现“继续前往 IP”,…...

Baumer工业相机堡盟相机如何使用偏振功能(偏振相机优点和行业应用)(C#)
项目场景: Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外࿰…...
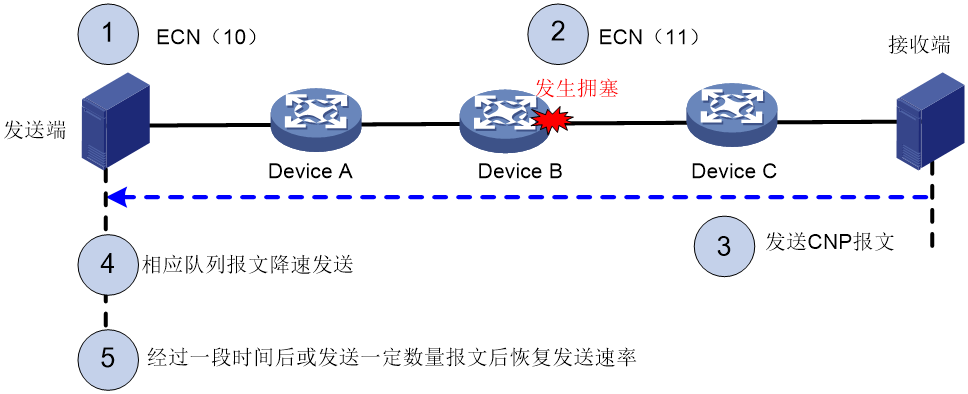
无损以太网与网络拥塞管理(PFC、ECN)
无损以太网 无损以太网(Lossless Ethernet)是一种专门用于数据中心网络的网络技术,旨在提供低延迟、高吞吐量和可靠性的传输服务。它是在传统以太网的基础上进行了扩展,引入了新的拥塞管理机制,以避免数据包丢失和网络…...

爬虫大全:从零开始学习爬虫的基础知识
爬虫是一种自动获取网站信息的技术,它可以帮助我们快速地抓取海量网站数据,进行统计分析、挖掘和展示。本文旨在为初学者详细介绍爬虫的基础知识,包括:爬虫原理、爬虫分类、网页结构分析、爬虫工具和技能、爬虫实践示范࿰…...

【Python】【进阶篇】21、Django Admin数据表可视化
目录 21、Django Admin数据表可视化1. 创建超级用户2. 将Model注册到管理后台1)在admin.py文件中声明 3. django_admin_log数据表 21、Django Admin数据表可视化 在《Django Admin后台管理系统》介绍过 Django 的后台管理系统是为了方便站点管理人员对数据表进行操作。Django …...

【MySQL约束】数据管理实用指南
1、数据库约束的认识 数据库约束的概念:数据库的约束是关系型数据库的一个重要的功能,它提供了一种“校验数据”合法性的机制,能够保证数据的“完整性”、“准确性”和“正确性” 数据库的约束: not null:不能存储 nul…...
2023年第二十届五一数学建模竞赛C题:“双碳”目标下低碳建筑研究-思路详解与代码答案
该题对于模型的考察难度较低,难度在于数据的搜集以及选取与处理。 这里推荐数据查询的网站:中国碳核算数据库(CEADs) https://www.ceads.net.cn/ 国家数据 国家数据data.stats.gov.cn/easyquery.htm?cnC01 以及各省市《统…...

Vue父组件生命周期和子组件生命周期触发顺序
加载渲染过程 父 beforeCreate -> 父 created -> 父 beforeMount -> 子 beforeCreate -> 子 created -> 子 beforeMount -> 子 mounted -> 父 mounted子组件更新过程 父 beforeUpdate -> 子 beforeUpdate -> 子 updated -> 父 updated父组件更新…...

DevOps工程师 - 面试手册
DevOps工程师 - 面试手册 岗位概述 DevOps工程师是一种专注于提高软件开发和运维团队协作、提高软件产品交付速度和质量的职位。这种角色要求具备跨领域的知识,以便在开发和运维过程中建立起稳定、可靠的基础设施和自动化流程。 常见的职位招聘描述 负责设计、实…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
