二叉搜索树中的众数
1题目
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
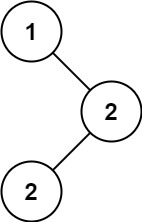
输入:root = [1,null,2,2] 输出:[2]
示例 2:
输入:root = [0] 输出:[0]
2链接
题目链接:501. 二叉搜索树中的众数 - 力扣(LeetCode)
视频链接:不仅双指针,还有代码技巧可以惊艳到你! | LeetCode:501.二叉搜索树中的众数_哔哩哔哩_bilibili
3解题思路
如果不是二叉搜索树
如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
具体步骤如下:
1、这个树都遍历了,用map统计频率
至于用前中后序哪种遍历也不重要,因为就是要全遍历一遍,怎么个遍历法都行,层序遍历都没毛病!
2、把统计的出来的出现频率(即map中的value)排个序
有的同学可能可以想直接对map中的value排序,还真做不到,C++中如果使用std::map或者std::multimap可以对key排序,但不能对value排序。
所以要把map转化数组即vector,再进行排序,当然vector里面放的也是pair<int, int>类型的数据,第一个int为元素,第二个int为出现频率。
3、取前面高频的元素
此时数组vector中已经是存放着按照频率排好序的pair,那么把前面高频的元素取出来就可以了。
是二叉搜索树
既然是搜索树,它中序遍历就是有序的。、
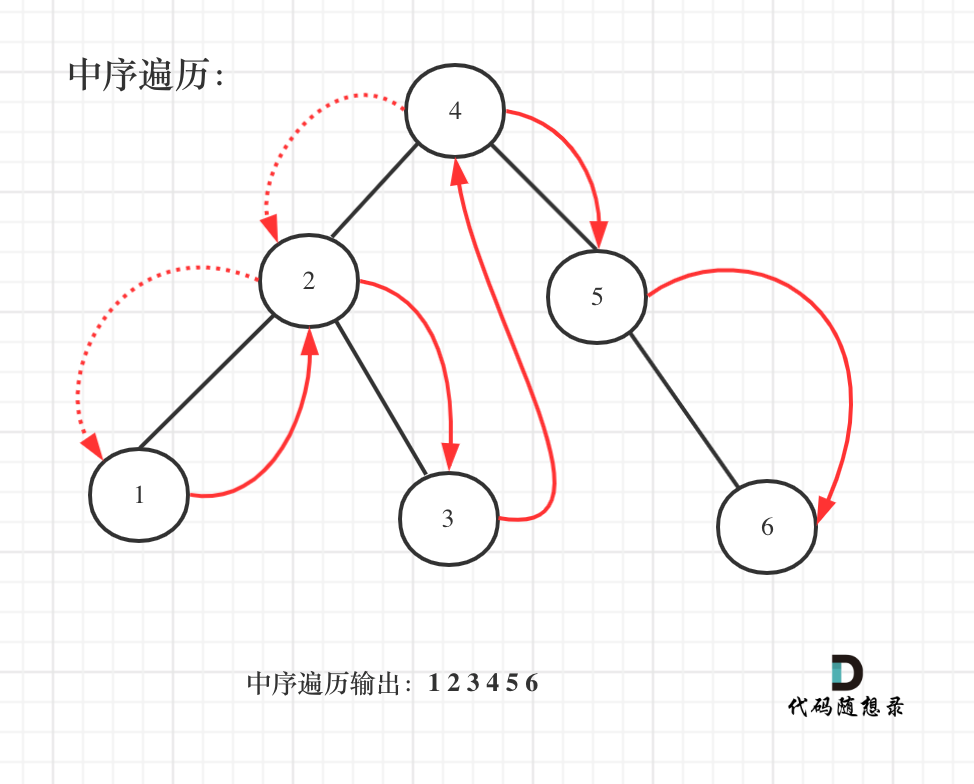
在二叉树:搜索树的最小绝对差 (opens new window)中我们就使用了pre指针和cur指针的技巧,这次又用上了。
弄一个指针指向前一个节点,这样每次cur(当前节点)才能和pre(前一个节点)作比较。
而且初始化的时候pre = NULL,这样当pre为NULL时候,我们就知道这是比较的第一个元素。
此时又有问题了,因为要求最大频率的元素集合(注意是集合,不是一个元素,可以有多个众数),如果是数组上大家一般怎么办?
应该是先遍历一遍数组,找出最大频率(maxCount),然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。(因为众数有多个)
这种方式遍历了两遍数组。
那么我们遍历两遍二叉搜索树,把众数集合算出来也是可以的。
但这里其实只需要遍历一次就可以找到所有的众数。
那么如何只遍历一遍呢?
如果 频率count 等于 maxCount(最大频率),当然要把这个元素加入到结果集中(以下代码为result数组)
result怎么能轻易就把元素放进去了呢,万一,这个maxCount此时还不是真正最大频率呢。
所以下面要做如下操作:
频率count 大于 maxCount的时候,不仅要更新maxCount,而且要清空结果集(以下代码为result数组),因为结果集之前的元素都失效了。
4代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///对任何二叉树都适用的传统方法
class Solution {
public:void searchBST(TreeNode* cur, unordered_map<int,int>& map) {if (cur == nullptr) return ;map[cur->val]++; //统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;}bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second;}vector<int> findMode(TreeNode* root) {unordered_map<int, int> map; //key:元素,value:出现的频率vector<int> result;if (root == nullptr) return result;searchBST(root, map);vector<pair<int, int>> vec(map.begin(), map.end());sort(vec.begin(), vec.end(), cmp); //给频率排序result.push_back(vec[0].first);for (int i = 1; i < vec.size(); i++) {//取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;}return result;}
};//双指针(pre & cur)法
class Solution {
public:int count = 0;int maxCount = 0;TreeNode* pre = nullptr;vector<int> result;void traversal (TreeNode* cur) {if (cur == nullptr) return ;//左traversal(cur->left); //中if (pre == nullptr) count = 1;else if (cur->val == pre->val) count++; //cur节点与pre节点数值相同,计数+1else count = 1; //cur节点与pre节点数值不相同,重置cur->val的计数pre = cur; //双指针依次后移if (count == maxCount) result.push_back(cur->val);// 如果和最大值相同,放进result中if (count > maxCount) {maxCount = count; //更新最大频率result.clear(); //清空result数组中储存的所有最大元素,因为找到了更大的result.push_back(cur->val); //把这个更大的元素放入result数组}//右traversal(cur->right);return ;}vector<int> findMode(TreeNode* root) {traversal(root);return result;}
};相关文章:

二叉搜索树中的众数
1题目 给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 如果树中有不止一个众数,可以按 任意顺序 返回。 假定 BST 满足如下定义&…...

认识JSP
什么是JSP? JSP(Java Server Pages)是一种类似于HTML的标记语言,用于创建动态Web页面。与HTML不同的是,JSP页面中可以嵌入Java代码,由Web服务器在动态页面中生成HTML代码,从而实现Web应用程序的前端交互效…...
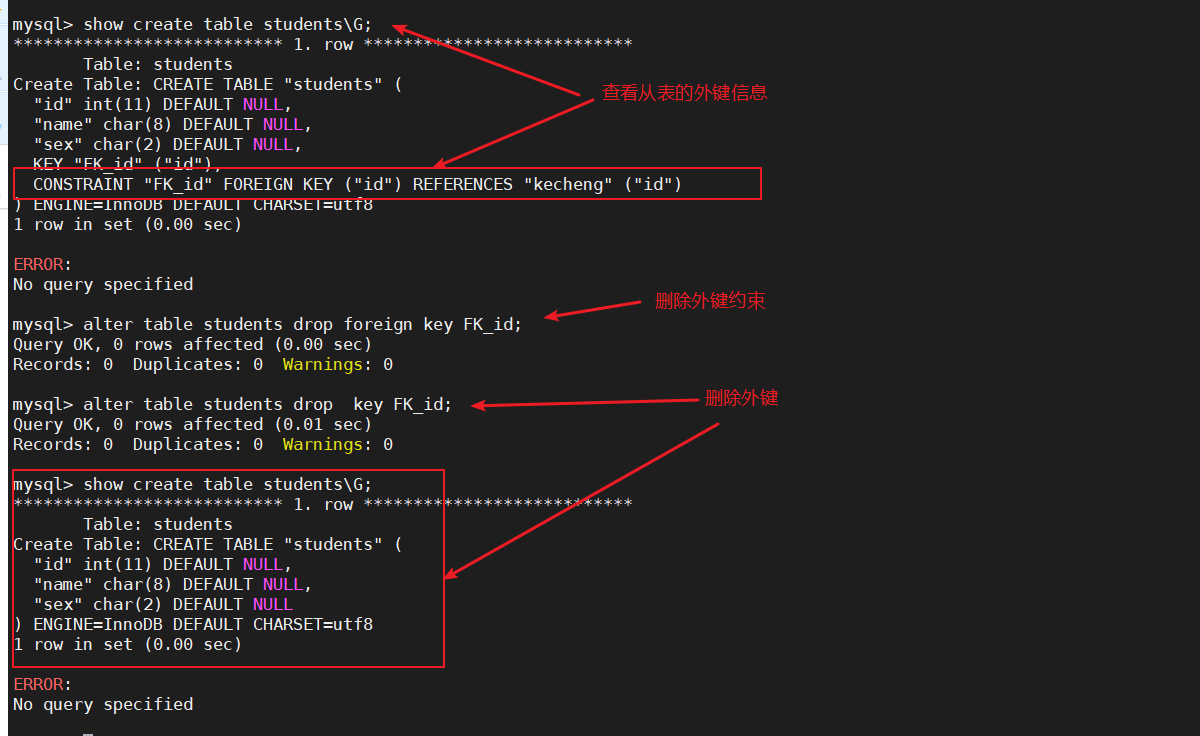
MySQL数据管理
一、MySQL数据库管理 1、库和表 行(记录):用来描述一个对象的信息 列(字段):用来描述对象的一个属性 2、常用的数据类型 int :整型 float :单精度浮点 4字节32位 double &…...
第十九章 Unity 其他 API
本节介绍一些其他经常使用的Unity类。首先,我们回顾一下Vector3向量类,它既可以表示方向,也可以表示大小。它在游戏中可以用来表示角色的位置,物体的移动/旋转,设置两个游戏对象之间的距离。在我们之前的课程中&#x…...

sha256算法详解,用C语言模拟sha256算法
SHA-256是一种加密算法,它可以将任意长度的数据块计算出一个固定长度的输出值,通常是256位。SHA-256具有以下特点: 1. 固定输出长度:SHA-256的输出长度为256位,不受输入数据的长度限制。 2. 不可逆性:SHA-256采用单向哈希函数,即无法从输出值反向推出输入数据。 3. 抗…...

前端技术未来发展展望
前端技术在未来的发展中将继续保持快速、变化多样和创新性强的趋势。以下是我认为前端技术未来发展的几个方向: 框架和库的演进:框架和库的更新换代将继续加速。React、Vue、Angular等主流框架的更新周期将会缩短,同时各自的生态系统也将更加…...

第四十六天|dp
今天的题还是完全背包的题 139. Word Break 这道题其实用deque也能做,但是需要cache去记录之前尝试过的值,.相对简单的办法就是用完全背包了 这道题worddict就是物品.我们的dp[i]代表到i为止是不是能满足题意分成segmentation 处置化全为false,但是dp[0]True.这是因为为0时…...
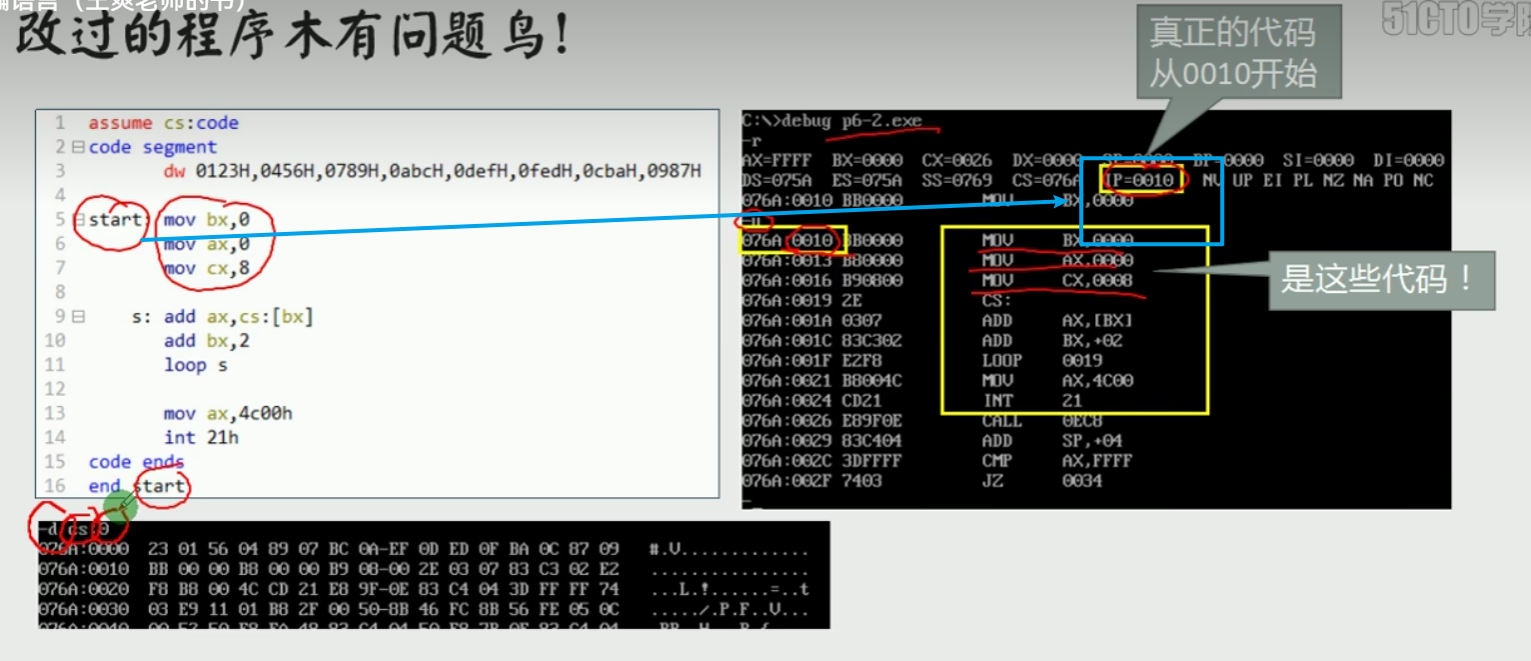
汇编语言-复习自用
本文用于自我复习汇编语言,参考b站一位老师的讲解整理而成,感谢老师的无私付出视频链接链接 文章目录 1.第一章1.1计算机组成1.2读取1.3 寄存器及数据存储1.4 mov和and指令1.5 确定物理地址1.6 内存分段表示法1.7debug使用1.8CS:IP1.9jmp指令改变csip1.1…...

Android moneky自动点击应用设想
近期又有人发错私密消息到群聊天里,造成巨大反应的事件,可谓是一失手成大恨,名利受损。 而如果手机里安装一个monkey自动点击程序,没事的时候,跑跑monkey,倒一杯茶,静静的看手机屏幕在那里点击&…...
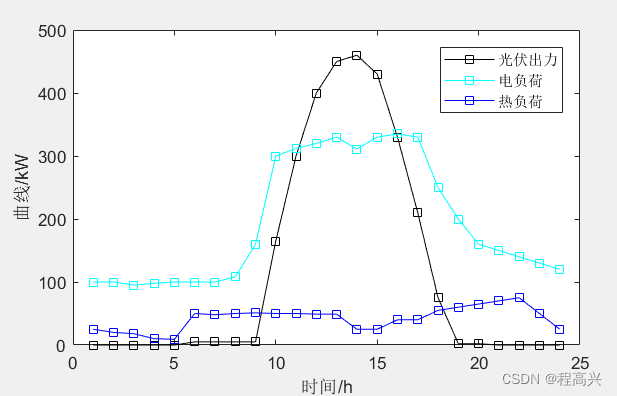
16.基于主从博弈理论的共享储能与综合能源微网优化运行研究
说明书 MATLAB代码:基于主从博弈理论的共享储能与综合能源微网优化运行研究 关键词:主从博弈 共享储能 综合能源微网 优化调度 参考文档:《基于主从博弈理论的共享储能与综合能源微网优化运行研究》完全复现 仿真平台:MATLAB …...

使用 ESP32 设计智能手表第 2 部分 - 环境光和心率传感器
我们研究了如何为我们的智能手表项目制作一些有趣的表盘。在这一部分中,我们将研究如何将一些传感器连接到我们的智能手表,并将连接 BH1750 环境光传感器和 MAX30102 心率传感器。我们将分别研究这些模块中的每一个的接口。 先决条件——安装必要的库 本文下方提供的 GitHub …...

分布式事务 --- 理论基础、Seata架构、部署
一、分布式事务问题 1.1、本地事务 本地事务,也就是传统的单机事务。在传统数据库事务中,必须要满足四个原则: 1.2、分布式事务 分布式事务,就是指不是在单个服务或单个数据库架构下,产生的事务,例如&am…...
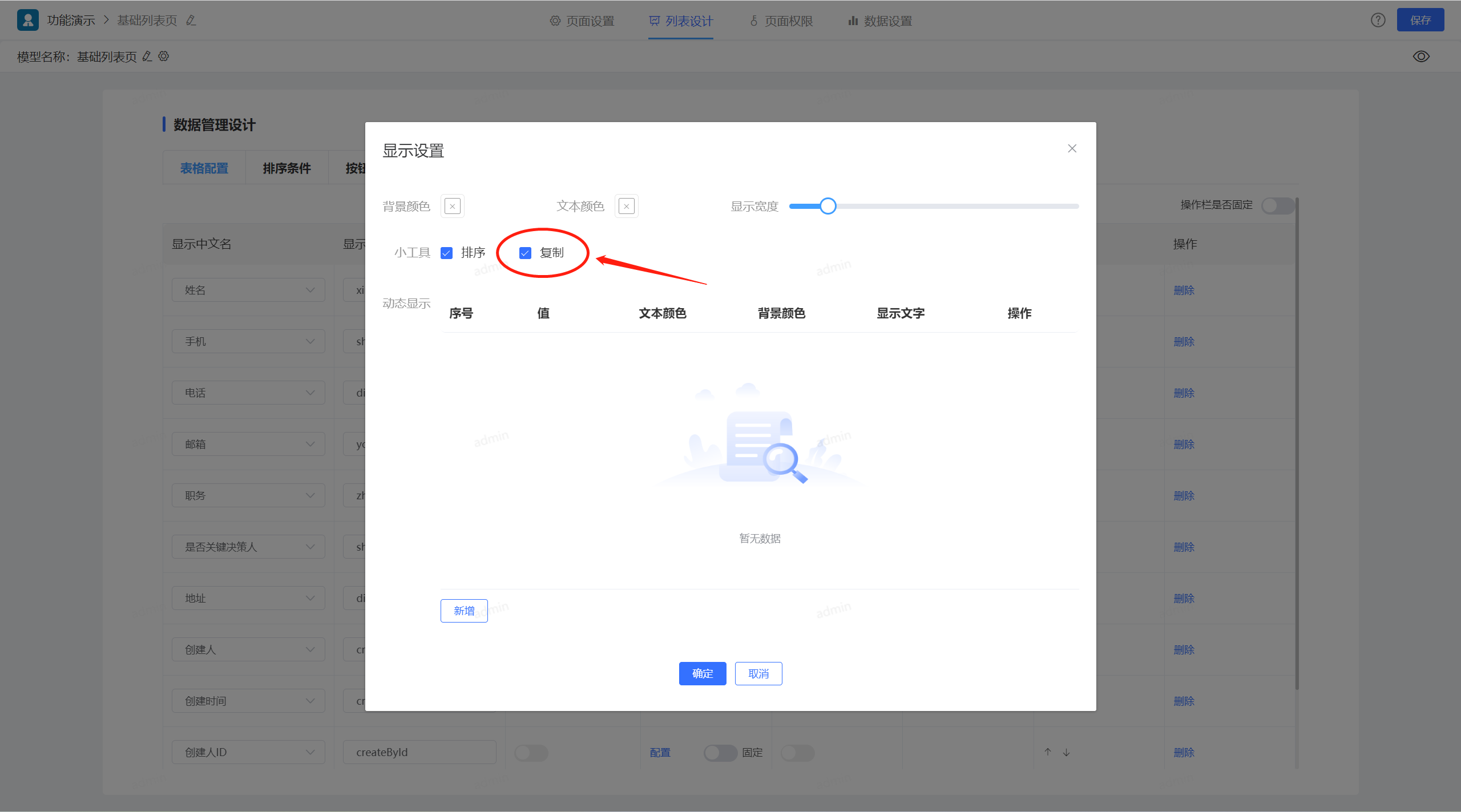
低代码开发重要工具:JVS列表页字段样式配置说明
列表页中,通常存在各种各样的样式控制,例如字段宽度需要可调、字段的颜色根据内容变化等,那么我们接下来介绍下字段的样式控制的内容以及对应的效果。 1、字段样式控制配置位置 进入列表页的 数据配置界面,每个字段可以有独立的配…...

explain结果字段分析
select_type simple:表示不需要union操作或者不包含子查询的简单select语句。有连接查询时,外层的查询为simple且只有一个。 primary:一个需要union操作或者含有子查询的select,位于最外层的单位查询的select_type即为primary且只…...

MySQL连接查询
MySQL连接查询 在多表联合查询时,为了减少查询的次数,使用连接查询可以一次查询多个相关联表的数据。 MySQL连接查询:分为内连接查询和外连接查询。 其中外连接查询又分成 left连接查询 和 right连接查询。 下午为两张数据库表,表…...
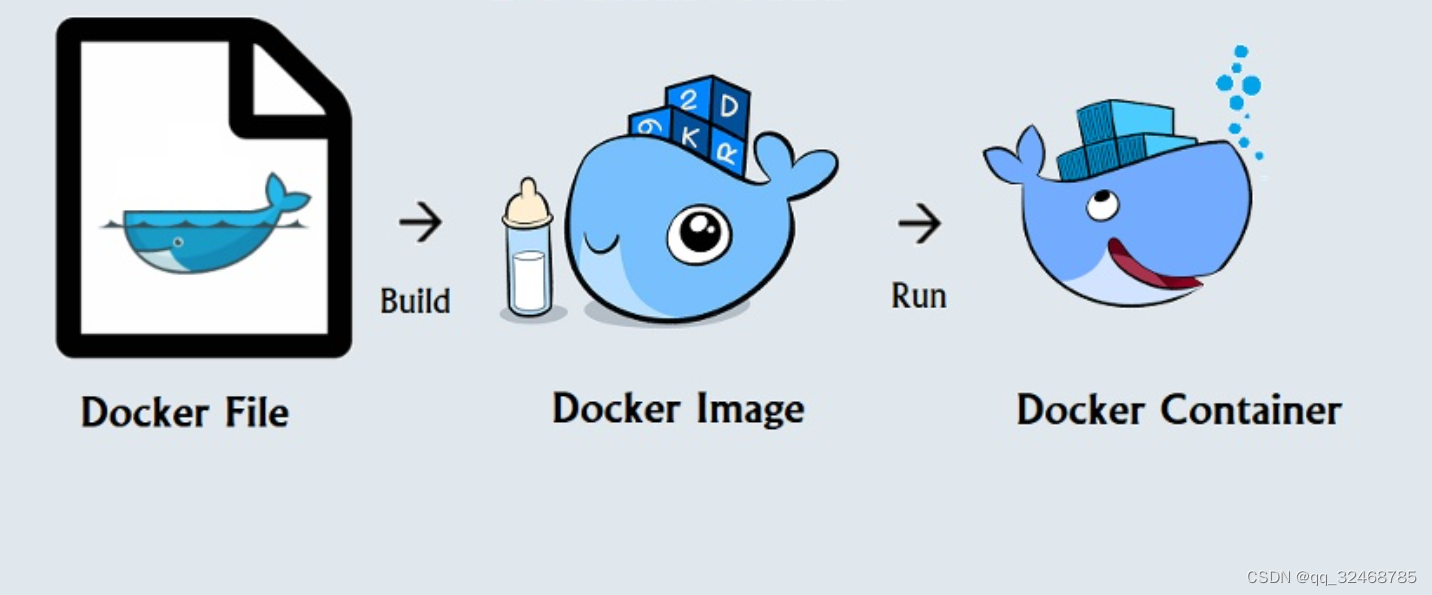
7. Docker——Dockerfile
本章讲解知识点 DockerfileDockerfile 常用命令Dockerfile 综合示例Docker Compose当我们理解了镜像的基本原理后,我们就可以开始 Dockerfile 的学习了。 1. Dockerfile Dockerfile 是用于构建 Docker 镜像的脚本。它包含一组指令,按顺序执行以创建 Docker 镜像,从而使其可…...

Input事件在应用中的传递(一)
Input事件在应用中的传递(一) hongxi.zhu 2023-4-25 前面我们已经梳理了input事件在native层的传递,这一篇我们接着探索input事件在应用中的传递与处理,我们将按键事件和触摸事件分开梳理,这一篇就只涉及按键事件。 一、事件的接收 从前面的…...

我在VScode学Java(Java一维数组)
我的个人博客主页:如果\真能转义1️⃣说1️⃣的博客主页 关于Java基本语法学习---->可以参考我的这篇博客:(我在Vscode学Java) 我在VScode学Java(Java一维数组) Java 一维数组 声明数组:先声明,后使用 动态分配内…...

不能使用chatGPT?这3个平替甚至比chatGPT更强
不能使用chatGPT?这3个平替甚至比chatGPT更强 chatGPT,一款由OpenAI开发的新型AI聊天机器人,正在势如破竹地改变着许多人的工作和生活方式。作为一款基于大语言模型的聊天机器人,chatGPT能够理解自然语言并进行人机对话。与传统的…...

基于SLM调制器,MIT研发高效率全息显示方案
此前,青亭网曾报道过NVIDIA、三星、剑桥大学等对空间光调制器(SLM)全息方案的探索。空间光调制器可调节光波的空间分布,在电驱动信号控制下,可改变光在空间中传播的振幅、强度、相位、偏振态等特性,从而形成…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
